倒立振子の安定化制御

[0] このページは、「SCILABによる倒立振子の特性解析」の続きです。以下では、物理定数を次のように仮定します。

$M=0.94$ [kg], $m=0.23$ [m], $\ell=0.6413/2$ [m], $\alpha=5$ [deg]

[1] まず，安定性を調べます。そのために，SCILABの関数specを用いて， $A$ 行列の固有値を求めると，次のように得られます。

$\lambda_1=0,\ \lambda_2=0,\ \lambda_3=+5.181,\ \lambda_4=-5.181$

したがって，３つの固有値の実部が負ではなく，漸近安定性の条件（すべての固有値の実部が負）を満足していません。よって，倒立振子は不安定な制御対象であると判定します。
次に，可制御性の判定を行ないます。そのために，可制御性行列の階数が，制御対象の次数４に等しいか，すなわち

${\rm rank}[B\ A-\lambda_i I_4]=4\quad(i=1,2,3,4)$

が成り立つかどうかを調べます。行列 $[B\ A-\lambda_iI_4]$ の最小特異値を求めると，次のように得られます。

$\begin{tabular}{l|l}\hline eigenvalues of A & minimum singular values of $[B\ A-\lambda_iI_4]$\\\hline \lambda_1=0 & \sigma_{min}=0.849\\ \lambda_2=0 & \sigma_{min}=0.849\\ \lambda_3=+5.181 & \sigma_{min}=0.434\\ \lambda_4=-5.181 & \sigma_{min}=0.434\\\hline \end{tabular}$

すべての最小特異値は正なので，倒立振子の可制御性は成り立つと判定します。

次に，可観測性の判定を行ないます。そのために，可観測性行列の階数が，制御対象の次数４に等しいか，すなわち

${\rm rank}\left[\begin{array}{c}C\\ A-\lambda_i I_4\end{array}\right]=4\quad(i=1,2,3,4)$

が成り立つかどうかを調べます。行列 $\left[\begin{array}{c}C\\ A-\lambda_i I_4\end{array}\right]$ の最小特異値を求めると，次のように得られます。

$\begin{tabular}{l|l}\hline eigenvalues of A & minimum singular values of $\left[\begin{array}{c}C\\ A-\lambda_i I_4\end{array}\right]$\\\hline \lambda_1=0 & \sigma_{min}=1\\ \lambda_2=0 & \sigma_{min}=1\\ \lambda_3=+5.181 & \sigma_{min}=0.189\\ \lambda_4=-5.181 & \sigma_{min}=0.189\\\hline \end{tabular}$

すべての最小特異値は正なので，倒立振子の可観測性は成り立つと判定します。

以上の計算を，SCILABで行うためのプログラムを，次に示します。

//cip.sce
M=0.94; m=0.23; ell=0.6413/2; g=9.8;
alpha=5/180*%pi
a32=-6*m*g/(8*M+(5-3*cos(2*alpha))*m);
b3=8/(8*M+(5-3*cos(2*alpha))*m);
a42=6*(M+m)*g/(8*M+(5-3*cos(2*alpha))*m)/ell;
b4=-6*cos(alpha)/(8*M+(5-3*cos(2*alpha))*m)/ell;
A=[0 0 1 0;0 0 0 1;0 a32 0 0;0 a42 0 0];
B=[0;0;b3;b4];
C=eye(2,4);
r=spec(A)
for i=1:4, min(svd([B A-r(i)*eye(4,4)])), end
for i=1:4, min(svd([C; A-r(i)*eye(4,4)])), end

[2] 不安定な倒立振子を安定化するための状態フィードバック

$u=-Fx$

を決定することを考えます。そのために安定な閉ループ系

$\dot{x}=(A-BF)x$

の応答に対して，２次形式評価関数

$\displaystyle{J=\int_0^\infty (q_1^2r^2(t)+q_2^2\dot{r}^2(t)+q_3^2\theta^2(t)+q_4^2\dot{\theta}^2(t)+\rho^2r_1^2u^2(t))dt}$

ただし、

$\displaystyle{q_1=\frac{1}{\max |r|},\ q_2=\frac{1}{\max |\dot{r}|},\ q_3=\frac{1}{\max |\theta|},\ q_4=\frac{1}{\max |\dot{\theta}|},\ r_1=\frac{1}{\max |u|}}$

を最小化するものを選ぶことを考えます。そのような安定化状態フードバックのゲイン行列 $F$ は，リッカチ方程式CARE

$\Pi A+A^T\Pi -\Pi B R^{-1} B^T\Pi+Q=0$

ただし、

$Q={\rm diag}\{q_1^2,q_2^2,q_3^2.q_4^2\},\ R=\rho^2r_1^2$

の解 $\Pi>0$ を用いて，次のように与えられます。

$F=R^{-1}B\Pi$

以上の計算を，SCILABで行うためのプログラムを，次に示します。

Mr=1; Tr=0.1; Mth=5/180*%pi;
Tth=(1/4)*(2*%pi*sqrt(4/3*ell/g)); Mu=5;
q1=1/Mr; q2=1/Mth; q3=Tr/Mr; q4=Tth/Mth; r1=1/Mu; rho=1;
Q=diag([q1^2,q2^2,q3^2,q4^2]); R=rho^2*r1^2;
//—–
function [F,p]=opt(A,B,C,Q,R)
w2=R\B’;
[v,p]=spec([A -B*w2;-C’*Q*C -A’]); p=diag(p);
[dummy,index]=sort(real(p));
n=size(A,1); j=index(n+1:n+n);
p=p(j); x=v(1:n,j); y=v(n+1:n+n,j);
X=real(y/x); F=w2*X;
endfunction
//—–
[F,p]=opt(A,B,eye(4,4),Q,R);
function dz=clps1(t,z),dz=(A-B*F)*z,endfunction
t0=0; t=0:0.01:10; x0=[0;3/180*%pi;0;0];
z=ode(x0,t0,t,clps1);
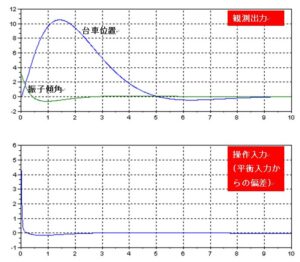
scf(0);
subplot(211),plot(t,diag([100 180/%pi])*C*z); mtlb_grid
subplot(212),plot(t,-F*z); mtlb_grid

計算工学演習第一レポート（２）

制御系CAD

制御を意識したモノつくりを目指して

倒立振子の安定化制御