モデル規範・SMオブザーバベース・追従SM制御…Homework
[1] 次の状態方程式で表される制御対象を考えます。
![]()
この状態が理想的なモデル
![]()
の状態を追従するように、すなわち
![]()
となるように制御則を決定したいとします。
以下では、(2)は適当な安定化状態フィードバックと入力変換を行って
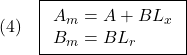
のように得られていると仮定します。
●モデル間の誤差は、(1)と(2)を辺々引き算して
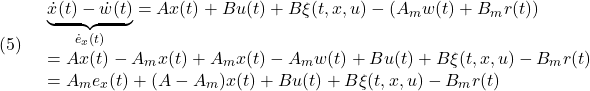
に従います。これは(4)を用いて次式となります。
![]()
●出力方程式は次式で与えられるとします。
![]()
状態フィードバックは使えないので、次のSMオブザーバを考えます。
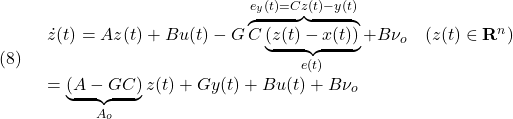
ここで、![]() は
は![]() が安定行列となるように選ばれているとします。
が安定行列となるように選ばれているとします。
SMオブザーバの誤差方程式は、(1)と(7)を辺々引き算して
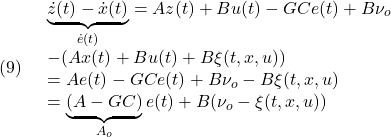
すなわち
![]()
となります。いま
![]()
を満足する![]() と、ある
と、ある![]() に対して
に対して
![]()
が満足されているものとします。このとき、![]() は次式で与えます。
は次式で与えます。
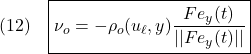
ただし
![]()
[2] SMオブザーバ(8)の状態((1)の状態の推定値)をモデル(2)の状態を追従させることを考えます。そのために次の制御則を考えます。
![]()
このとき、この場合のモデル間の誤差は、(8)と(2)を辺々引き算して
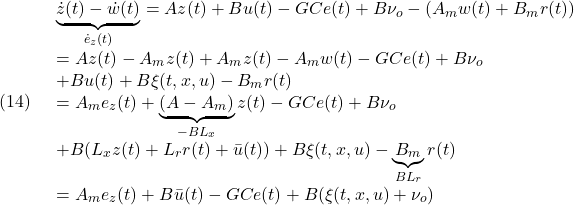
すなわち
![]()
に従います。これに対して、スライディングモード制御
![]()
を適用することを考えます。スイッチング関数は
![]()
とします。これはスイッチング関数(1)またはスイッチング関数(2)の方法で選定します。
●線形制御部を、次式のように決めます。
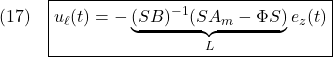
また、スイッチング部を、次式のように決めます。
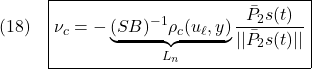
ここで、![]() は適当な安定行列
は適当な安定行列![]() を与えて
を与えて
![]()
の解として求め、また、次の関係を満たすものとします。
![]()
●(15),(18)を(14′)に代入して、モデル間の誤差は
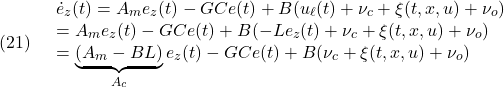
すなわち
![]()
に従います。
[3] 以下では、状態方程式は次のSM標準形をとるように座標変換されているとします。
![Rendered by QuickLaTeX.com \displaystyle{(22)\quad \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} (u(t)+\xi(t,x,u)) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-afe711daafabb0f12e447bb07a3ace73_l3.png)
これに応じて、スイッチング関数(16)を
![Rendered by QuickLaTeX.com \displaystyle{(23)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} e_{z1}(t)\\ e_{z2}(t) \end{array}\right] }_{x(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I_m \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} e_{z1}(t)\\ e_{z2}(t) \end{array}\right] }_{x(t)} \ (M=S_2^{-1}S_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d0776a59ef9ed32eda82a08310faf1f3_l3.png)
と分割します。
(21)は、![]() と
と![]() に注意して
に注意して
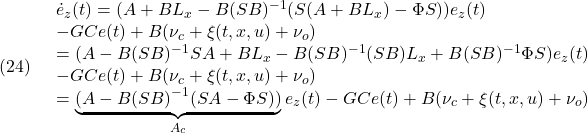
となります。これに対して座標変換
![Rendered by QuickLaTeX.com \displaystyle{(25)\quad \begin{array}{l} \underbrace{\left[\begin{array}{c} e_{z1}(t)\\ s(t) \end{array}\right]}_{\bar{e}_z(t)}= \underbrace{\left[\begin{array}{cc} I_{n-m} & 0_{n\times m} \\ S_1 & S_2 \\ \end{array}\right]}_{\bar T} \underbrace{\left[\begin{array}{c} e_{z1}(t)\\ e_{z2}(t) \end{array}\right]}_{e_z(t)}\\ \Leftrightarrow \underbrace{\left[\begin{array}{c} e_{z1}(t)\\ e_{z2}(t) \end{array}\right]}_{e_z(t)}= \underbrace{\left[\begin{array}{cc} I_{n} & 0_{n\times m} \\ -M & S_2^{-1} \\ \end{array}\right]}_{\bar{T}^{-1}} \underbrace{\left[\begin{array}{c} e_{z1}(t)\\ s(t) \end{array}\right]}_{\bar{e}_z(t)}\quad(M=S_2^{-1}S_1) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-348e24095f272550ca7b0d85c1be93cf_l3.png)
を行うと、まず(25)を(24)に代入して
![Rendered by QuickLaTeX.com \displaystyle{(26)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc} I & 0 \\ -M & S_2^{-1} \\ \end{array}\right] }_{\bar{T}^{-1}} \underbrace{ \left[\begin{array}{c} \dot e_{z1}(t)\\ \dot s(t) \end{array}\right] }_{\dot{\bar{e}}_z(t)}\\ = (\left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] - \left[\begin{array}{c} 0\\ B_2 \end{array}\right] (\left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] \left[\begin{array}{c} 0\\ B_2 \end{array}\right])^{-1}\\ \times(\left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] -\Phi \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right]) ) \underbrace{ \left[\begin{array}{cc} I & 0 \\ -M & S_2^{-1} \\ \end{array}\right] }_{\bar{T}^{-1}} \underbrace{ \left[\begin{array}{c} e_{z1}(t)\\ s(t) \end{array}\right] }_{\bar{e}_z(t)}\\ -G Ce(t)+\left[\begin{array}{c} 0\\ B_2 \end{array}\right](\nu_c+\xi(t,x,u)+\nu_o) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8b57169deafca1bae478ad161a8da6bc_l3.png)
左から![]() をかけて
をかけて
![Rendered by QuickLaTeX.com \displaystyle{(27)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot e_{z1}(t)\\ \dot s(t) \end{array}\right] }_{\dot{\bar{e}}_z(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{\bar{T}} (\left[\begin{array}{cc} A_{11}-A_{12}M & A_{12}S_2^{-1} \\ A_{21}-A_{22}M & A_{22}S_2^{-1} \\ \end{array}\right] -\left[\begin{array}{c} 0\\ B_2 \end{array}\right](S_2B_2)^{-1}\\ \times(\left[\begin{array}{cc} S_1 & S_2 \end{array}\right] \left[\begin{array}{cc} A_{11}-A_{12}M & A_{12}S_2^{-1} \\ A_{21}-A_{22}M & A_{22}S_2^{-1} \\ \end{array}\right] -\Phi \left[\begin{array}{cc} 0 & I_m \\ \end{array}\right]) ) \underbrace{ \left[\begin{array}{c} e_{z1}(t)\\ s(t) \end{array}\right] }_{\bar{e}_z(t)}\\ -\underbrace{\bar{T}G}_{\bar{G}} Ce(t) +\underbrace{\left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right]}_{\bar{T}} \left[\begin{array}{c} 0\\ B_2 \end{array}\right](\nu_c+\xi(t,x,u)+\nu_o)\\ = (\left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ \bar{A}_{21} & \bar{A}_{22}\\ \end{array}\right] -\left[\begin{array}{c} 0\\ S_2B_2 \end{array}\right](S_2B_2)^{-1}\\ \times(\left[\begin{array}{cc} \bar{A}_{21} & \bar{A}_{22}\\ \end{array}\right] -\Phi \left[\begin{array}{cc} 0 & I_m \\ \end{array}\right]) ) \underbrace{ \left[\begin{array}{c} e_{z1}(t)\\ s(t) \end{array}\right] }_{\bar{e}_z(t)}\\ -\bar{G} Ce(t)+\bar{B}(\nu_c+\xi(t,x,u)+\nu_o)\\ =\underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ 0 & \Phi\\ \end{array}\right]}_{A_c} \underbrace{ \left[\begin{array}{c} e_{z1}(t)\\ s(t) \end{array}\right] }_{\bar{e}_z(t)} -\bar{G} Ce(t) +\underbrace{\left[\begin{array}{c} 0\\ S_2B_2 \end{array}\right]}_{\bar{B}}(\nu_c+\xi(t,x,u)+\nu_o) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2b1c5781518b0452b1e2a88534ac95c5_l3.png)
ただし
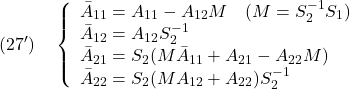
を得ます。ここで、![]() が安定行列となるように行列
が安定行列となるように行列![]() が選ばれているとします。
が選ばれているとします。
これを誤差方程式(9′)と合わせて、閉ループ系は次式で表されます。
![Rendered by QuickLaTeX.com \displaystyle{(28)\quad \begin{array}{l} \left[\begin{array}{c} \dot{e}(t)\\ \dot{\bar{e}}_z(t) \end{array}\right]= \underbrace{\left[\begin{array}{cc} A_o & 0\\ -\bar{G}C & A_c \end{array}\right]}_{A_G} \left[\begin{array}{c} e(t)\\ \bar{e}_z(t) \end{array}\right]\\ + \left[\begin{array}{c} 0\\ \bar{B} \end{array}\right]{\nu}_c + \left[\begin{array}{c} B\\ \bar{B} \end{array}\right]\nu_o + \left[\begin{array}{c} -B\\ \bar{B} \end{array}\right]\xi(t,x,\hat{u}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4780b23f37e18adf37d5716a3c232cfb_l3.png)
●以上に基づく設計手順を、数値例で示します。
| MATLAB |
|

図1 モデル規範・SMオブザーバベース・追従SM制御系のシミュレーション例
Note C93 閉ループ系の安定性
●閉ループ系のダイナミックスは次式で表されます。
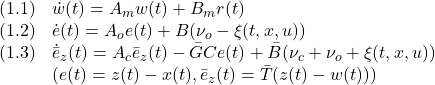
ただし
![Rendered by QuickLaTeX.com \displaystyle{(1.4)\quad \begin{array}{l} A_m=A+BL_x,\ B_m=BL_r\\ A_o=A-GC\\ A_c=\bar{T}(A_m-BL)\bar{T}^{-1}\\ L=(SB)^{-1}(SA_m-\Phi S)\\ \bar{B}=\left[\begin{array}{c} 0\\ S_2B_2 \end{array}\right],\ \bar{G}=\bar{T}G \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5af9937c0ebb7b0466617bc2ea71afbe_l3.png)
これに対して次のリャプノフ関数を考えます。
![]()
ここで、正定行列![]() 、
、![]() は、それぞれ安定行列
は、それぞれ安定行列![]() 、
、![]() のリャプノフ行列とし、次のリャプノフ方程式の解とします。
のリャプノフ行列とし、次のリャプノフ方程式の解とします。
![]()
●![]() は、リャプノフ方程式
は、リャプノフ方程式
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \underbrace{\left[\begin{array}{cc} \bar{P}_1 & 0\\ 0 & \bar{P}_2 \end{array}\right]}_{\bar P} \underbrace{\left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12}\\ 0 & \Phi \end{array}\right]}_{A_c} +\underbrace{\left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12}\\ 0 & \Phi \end{array}\right]^T}_{A_c^T} \underbrace{\left[\begin{array}{cc} \bar{P}_1 & 0\\ 0 & \bar{P}_2 \end{array}\right]}_{\bar P}<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9f1e612deced36f7c7db9b14fc59dc21_l3.png)
を満足するブロック対角行列とします。ここで、正定行列![]() 、
、![]() は、それぞれ安定行列
は、それぞれ安定行列![]() 、
、![]() に対する次のリャプノフ不等式の解です。
に対する次のリャプノフ不等式の解です。
![]()
![]()
このとき、![]() と
と![]() は、次のリャプノフ不等式の解を構成するとします。
は、次のリャプノフ不等式の解を構成するとします。
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \underbrace{\left[\begin{array}{cc} P & 0\\ 0 & \bar{P} \end{array}\right]}_{P_G} \underbrace{\left[\begin{array}{cc} A_o & 0\\ -\bar{G}C & A_c \end{array}\right]}_{A_G} +\underbrace{\left[\begin{array}{cc} A_o & 0\\ -\bar{G}C & A_c \end{array}\right]^T}_{A_G^T} \underbrace{\left[\begin{array}{cc} P & 0\\ 0 & \bar{P} \end{array}\right]}_{P_G}<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dceeb6208f924a3f6efeaa77bb099a32_l3.png)
これは次式と等価です。
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \underbrace{\left[\begin{array}{cc} PA_o & 0\\ -\bar{P}\bar{G}C & \bar{P}A_c \end{array}\right]}_{P_GA_G}+ \underbrace{\left[\begin{array}{cc} PA_o & 0\\ -\bar{P}\bar{G}C & \bar{P}A_c \end{array}\right]^T}_{(P_GA_G)^T} =\left[\begin{array}{cc} -Q & -C^T\bar{G}^T\bar{P}\\ -\bar{P}\bar{G}C & \bar{P}A_c+A_c^T\bar{P} \end{array}\right]<0\\ \Leftrightarrow \bar{P}A_c+A_c^T\bar{P}+\bar{P}\bar{G}CQ^{-1}C^T\bar{G}^T\bar{P}<0\\ \Leftrightarrow A_c\bar{P}^{-1}+\bar{P}^{-1}A_c^T+\bar{G}CQ^{-1}C^T\bar{G}^T<0\\ \Leftrightarrow A_c\bar{P}^{-1}+\bar{P}^{-1}A_c^T+\bar{G}CQ^{-1}C^T\bar{G}^T=-\bar{Q}\quad(\bar{Q}>0) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c62b77d490c2fb89c0065a176246cf86_l3.png)
ここで、新しいパラメータ![]() を導入し、次の公式を用いています。
を導入し、次の公式を用いています。
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{lll} && \left[\begin{array}{cc} P & M \\ M^T & Q \end{array}\right]<0\\ &\Leftrightarrow& P-MQ^{-1}M^T<0,\ Q<0\\ &\Leftrightarrow& P<0,\ Q-M^TP^{-1}M<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-eee622434bc9e2fc505eb899dbb107cb_l3.png) |
いま適当な![]() と
と![]() を与えて、
を与えて、
![]()
![]()
を解いて、![]() と
と![]() を定めるものとします。このとき(7)は
を定めるものとします。このとき(7)は
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} \underbrace{\left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12}\\ 0 & \Phi \end{array}\right]}_{A_c} \underbrace{\left[\begin{array}{cc} \bar{P}_1^{-1} & 0\\ 0 & \bar{P}_2^{-1} \end{array}\right]}_{\bar{P}^{-1}} + \underbrace{\left[\begin{array}{cc} \bar{P}_1^{-1} & 0\\ 0 & \bar{P}_2^{-1} \end{array}\right]}_{\bar{P}^{-1}} \underbrace{\left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12}\\ 0 & \Phi \end{array}\right]^T}_{A_c^T}\\ +\underbrace{\left[\begin{array}{c} \bar{G}_1\\ \bar{G}_2 \end{array}\right]}_{\bar{G}} \underbrace{CQ^{-1}C^T}_{Q_{22}} \underbrace{\left[\begin{array}{c} \bar{G}_1\\ \bar{G}_2 \end{array}\right]^T}_{\bar{G}^T}\\ = \underbrace{\left[\begin{array}{cc} \bar{A}_{11}\bar{P}_1^{-1} & \bar{A}_{12}\bar{P}_2^{-1}\\ 0 & \Phi \bar{P}_2^{-1} \end{array}\right]}_{A_c\bar{P}^{-1}} + \underbrace{\left[\begin{array}{cc} \bar{A}_{11}\bar{P}_1^{-1} & \bar{A}_{12}\bar{P}_2^{-1}\\ 0 & \Phi \bar{P}_2^{-1} \end{array}\right]^T}_{(A_c\bar{P}^{-1})^T}\\ +\underbrace{\left[\begin{array}{cc} \bar{G}_1Q_{22}\bar{G}_1^T &\bar{G}_1Q_{22}\bar{G}_2^T\\ \bar{G}_2Q_{22}\bar{G}_1^T &\bar{G}_2Q_{22}\bar{G}_2^T \end{array}\right]}_{\bar{G}CQ^{-1}C^T\bar{G}^T}\\ = \left[\begin{array}{cc} \bar{A}_{11}\bar{P}_1^{-1}+\bar{P}_1^{-1}\bar{A}_{11}^T+\bar{G}_1Q_{22}\bar{G}_1^T & \bar{A}_{12}\bar{P}_2^{-1}+\bar{G}_1Q_{22}\bar{G}_2^T\\ \bar{P}_2^{-1}\bar{A}_{12}^T+\bar{G}_2Q_{22}\bar{G}_1^T & \Phi\bar{P}_2^{-1}+\bar{P}_2^{-1}\Phi^T+\bar{G}_2Q_{22}\bar{G}_2^T \end{array}\right]\\ = \left[\begin{array}{cc} -\hat{Q}_1+\bar{G}_1Q_{22}\bar{G}_1^T & \bar{A}_{12}\bar{P}_2^{-1}+\bar{G}_1Q_{22}\bar{G}_2^T\\ \bar{P}_2^{-1}\bar{A}_{12}^T+\bar{G}_2Q_{22}\bar{G}_1^T & -\hat{Q}_2+\bar{G}_2Q_{22}\bar{G}_2^T \end{array}\right]<0\\ \Leftrightarrow \left\{\begin{array}{l} \bar{G}_1Q_{22}\bar{G}_1^T +(\bar{A}_{12}\bar{P}_2^{-1}+\bar{G}_1Q_{22}\bar{G}_2^T)\\ \times(\bar{G}_2Q_{22}\bar{G}_2^T -\hat{Q}_2)^{-1}(\bar{P}_2^{-1}\bar{A}_{12}^T+\bar{G}_2Q_{22}\bar{G}_1^T) <\hat{Q}_1\\ \bar{G}_2Q_{22}\bar{G}_2^T <\hat{Q}_2 \end{array}\right. \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d2a4be3ea4336e3bad8a74302a1a87d8_l3.png)
となります。したがって、この制約を(8)の![]() 、(9)の
、(9)の![]() に付けておきます。
に付けておきます。
●以上の準備の下で次式が示され、閉ループ系のリャプノフ安定性が成り立ちます。

ここで、次の平方完成を行っています。
![]()
また、次が成り立つことを用いています。
![]()
まず、(14.1)は
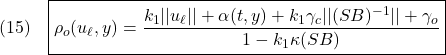
を仮定すると、これを変形して得られる
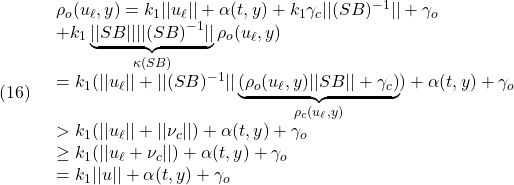
を用いて
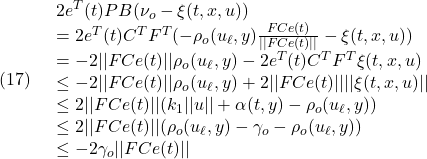
次に、(14.2)は
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \begin{array}{l} 2\bar{e}_z^T(t)\bar{P}\bar{B}(\nu_c+\nu_o+\xi(t,x,u))\\ =2\underbrace{\left[\begin{array}{c} e_{z1}(t)\\ s(t) \end{array}\right]^T}_{\zeta^T(t)} \underbrace{\left[\begin{array}{cc} \bar{P}_1 & 0\\ 0 & \bar{P}_2 \end{array}\right]}_{\bar P} \underbrace{\left[\begin{array}{c} 0\\ S_2B_2 \end{array}\right]}_{\bar{B}}(\nu_c+\nu_o+\xi(t,x,u))\\ =-2s^T(t)\bar{P}_2(S_2B_2)\rho_o(u_\ell,y)\frac{FCe(t)}{||FCe(t)||}\\ -2s^T(t)\bar{P}_2(S_2B_2)(S_2B_2)^{-1}\rho_c(u_\ell,y) \frac{\bar{P}_2s(t)}{||\bar{P}_2s(t)||}+2s^T(t)\bar{P}_2(S_2B_2)\xi(t,x,u)\\ =-2s^T(t)\bar{P}_2(S_2B_2)\rho_o(u_\ell,y)\frac{B^TPe(t)}{||B^TPe(t)||}\\ -2s^T(t)\bar{P}_2\rho_c(u_\ell,y)\frac{\bar{P}_2s(t)}{||\bar{P}_2s(t)||}+2s^T(t)\bar{P}_2(S_2B_2)\xi(t,x,u)\\ \le 2||\bar{P}_2s(t)||||S_2B_2||\rho_o(u_\ell,y)-2\rho_c(u_\ell,y)||\bar{P}_2s(t)||\\ +2||\bar{P}_2s(t)||||S_2B_2||||\xi(t,x,u)||\\ \le 2||\bar{P}_2s(t)||(\rho_o(u_\ell,y)||S_2B_2||-\rho_c(u_\ell,y))\\ +2||\bar{P}_2s(t)||||S_2B_2||(k_1||u||+\alpha(t,y))\\ \le 2||\bar{P}_2s(t)||(\rho_c(u_\ell,y)-\gamma_c-\rho_c(u_\ell,y))\\ +2||\bar{P}_2s(t)||||S_2B_2||(\rho_o(u_\ell,y)-\gamma_o)\\ =-2\underbrace{(\gamma_c-||S_2B_2||(\rho_o(u_\ell,y)-\gamma_o))}_{\gamma_c'}||\bar{P}_2s(t)|| \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b653afff2b1cd408b6383ca8513746bc_l3.png)