応用例…Homework
[1] ある航空機の線形状態方程式として、次を考えます。
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} \dot{x}(t)=Ax(t)+Bu(t)\\ x(t)= \left[\begin{array}{ll} \theta & pitch\ angle\\ q & pitch\ rate\\ \alpha & angle\ of\ atack\\ \eta & elevator\ deflection\\ \delta & flap\ deflection \end{array}\right],\quad u(t)= \left[\begin{array}{ll} \eta_c & elevator\ command\\ \delta_c& flap\ comannd \end{array}\right]\\ A=\left[\begin{array}{rrrrr} 0 & 1 & 0 & 0 & 0\\ 0 &-1.99 & -13.41 & -18.95 & -3.60\\ 0 & 1 & -1.74 & -0.08 & -0.59\\ 0 & 0 & 0 & -20 & 0\\ 0 & 0 & 0 & 0 & -20 \end{array}\right],\quad B=\left[\begin{array}{rr} 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 20 & 0\\ 0 & 20 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e8e30c3e5083c206da3951e3e40e9cfb_l3.png)
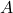 行列の固有値は次のように求められます。
行列の固有値は次のように求められます。

状態変数として、pitch angle 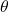 の代わりに、fligt path angle
の代わりに、fligt path angle 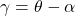 を用いると、次式となります。
を用いると、次式となります。
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \begin{array}{l} \dot{x}(t)=Ax(t)+Bu(t)\\ x(t)= \left[\begin{array}{ll} \gamma=\theta-\alpha & fligt\ path\ angle\\ q & pitch\ rate\\ \alpha & angle\ of\ atack\\ \eta & elevator\ deflection\\ \delta & flap\ deflection \end{array}\right],\quad u(t)= \left[\begin{array}{ll} \eta_c & elevator\ command\\ \delta_c& flap\ comannd \end{array}\right]\\ A=\left[\begin{array}{rrrrr} 0 & 0 & 1.74 & 0.08 & 0.59\\ 0 &-1.99 & -13.41 & -18.95 & -3.60\\ 0 & 1 & -1.74 & -0.08 & -0.59\\ 0 & 0 & 0 & -20 & 0\\ 0 & 0 & 0 & 0 & -20 \end{array}\right],\quad B=\left[\begin{array}{rr} 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 20 & 0\\ 0 & 20 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b3ae110ebe0cc483c67a6db0b309e181_l3.png)
また、評価変数は、pitch angle 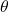 とfligt path angle
とfligt path angle 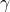 とすると、その出力方程式は次式のように与えられます。
とすると、その出力方程式は次式のように与えられます。
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} y(t)=Hx(t)\\ H= \left[\begin{array}{ccccc} 1 & 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c44cf07d269341a588b528f5aca4caf9_l3.png)
制御目的は、次図のように、pitch angle 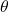 とfligt path angle
とfligt path angle 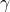 の間の非干渉化を達成し、独立して設定値に合せることです。
の間の非干渉化を達成し、独立して設定値に合せることです。
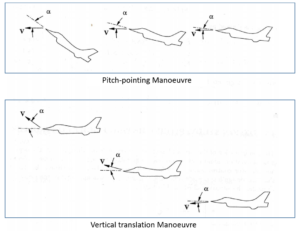
図1 航空機の操縦法
[3] 積分動作導入による追従制御
この場合の制御則は次のように構成されます。
![Rendered by QuickLaTeX.com \displaystyle{(20)\quad { \boxed{\begin{array}{l} u(t)=u_\ell(t)+u_n(t)\\ u_\ell(t)=-\underbrace{(SB_E)^{-1}(SA_E-\Phi S)}_{L=L_{eq}+L_\Phi}\left[\begin{array}{c} x_r(t)\\ x(t) \end{array}\right]\\ -\underbrace{(SB_E)^{-1}(\Phi S_r+S_1B_r)}_{L_r} r(t) +\underbrace{(SB_E)^{-1}S_r}_{L_{\dot r}} \dot{r}(t)\\ u_n(t)=-\underbrace{(SB_E)^{-1}\rho(t,x)}_{L_n}\frac{P_2(s(t)-S_rr(t))}{||P_2(s(t)-S_rr(t))||} \end{array}}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-adc6bfdf1b50ea9ed3b1152bc4ee1729_l3.png)
●ここでは、等価制御による閉ループ系の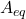 が望ましい固有値・固有ベクトルをもつように設計して、次式からスイッチング関数を決める行列
が望ましい固有値・固有ベクトルをもつように設計して、次式からスイッチング関数を決める行列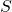 を決定します。
を決定します。
![Rendered by QuickLaTeX.com \displaystyle{(21)\quad { S[v_1\cdots v_{n-m}]=0 % \Rightarrow [v_1\cdots v_{n-m}]^TS^T=0} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4790019052495c30728e57e082b109a1_l3.png)
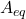 の望ましい固有値を
の望ましい固有値を
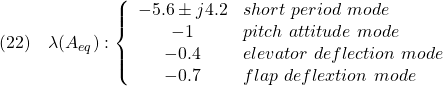
とし、また望ましいモード分布を次により指定します。
![Rendered by QuickLaTeX.com \displaystyle{(23)\quad {\tt specpos}= \left[\begin{array}{ccccc} 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\\hline 1 & 1 & 1 & 1 & 1\\ 1 & 0 & 1 & 1 & 1\\ 0 & 1 & 1 & 0 & 1\\\hline 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\ \end{array}\right],\quad {\tt specent}= \left[\begin{array}{rrrrr} -1 & -1 & -1 & -1 & -1\\ -1 & -1 & -1 & -1 & -1\\\hline 0 & 0 & 1 & 0 & 1\\ 1 & -1 & 0 & 1 & 0\\ -1 & 1 & 0 & -1 & 0\\\hline -1 & -1 & -1 & -1 & -1\\ -1 & -1 & -1 & -1 & -1\\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0c718bed933ebbd16e58b62392705e36_l3.png)
このとき次のような行列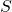 を得ます。
を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(24)\quad S=\left[\begin{array}{rrrrr|rr} 0.0531 & 0.0137 & -0.1436 & -0.0260 & -0.1373 & 0.0500 & 0\\ -0.0072 & -0.0612 & 0.1635 & 0.0035 & 0.1661 & 0 & 0.0500 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e2f04984ddc7627313559a7fba4fb029_l3.png)
このときSMC則における行列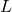 などは次のように計算されます。
などは次のように計算されます。
![Rendered by QuickLaTeX.com \displaystyle{(25)\quad L=\left[\begin{array}{rrrrrrr} -1.0616 & -0.2743 & 2.9379 & 0.6060 & 2.4605 & -0.4927 & -0.0900\\ 0.1440 & 1.2236 & -3.3390 & -0.2296 & -3.2769 & 0.0671 & 0.0142 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-65ba95f5e903558942fd235961ffdedf_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(26)\quad L_{r}=\left[\begin{array}{rr} -2.9499 & 0.0120\\ 0.4000 & 2.9391 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ff4217b946efcf865f3cf36ef51739bf_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(27)\quad L_{\dot{r}}=\left[\begin{array}{rr} -0.1448 & 0.0013\\ 0.0196 & 0.1439 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5bdd8c981f643ce02c26b921c6ef3e2e_l3.png)
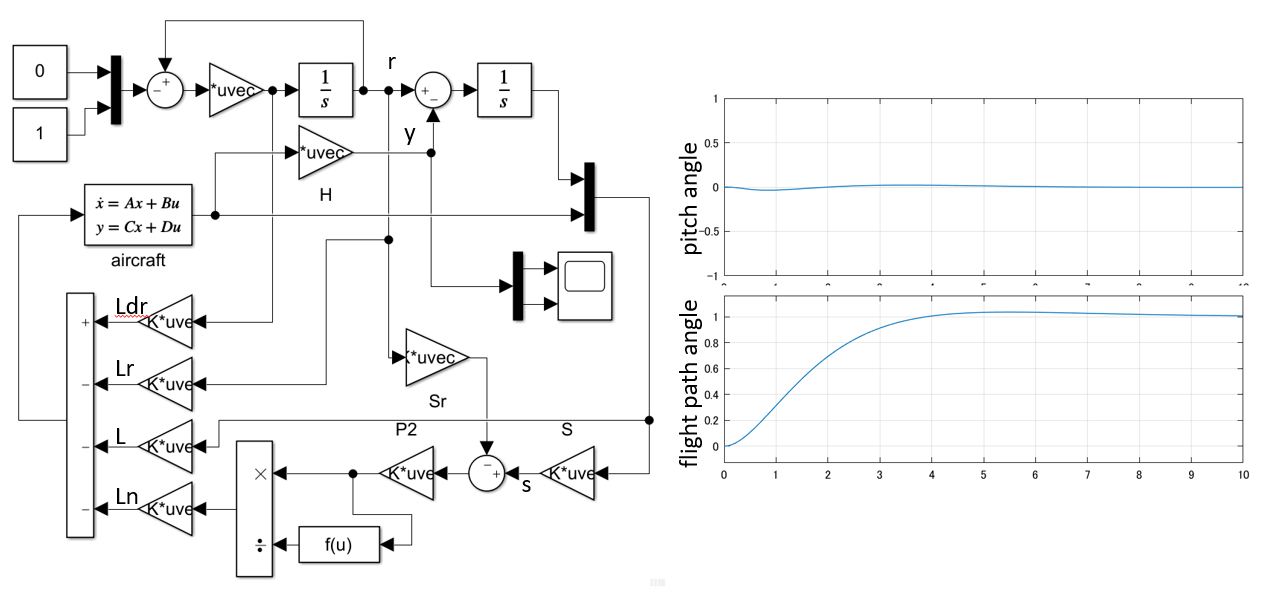
図2 積分動作導入によるSMC制御系応答
| MATLAB |
%cAITCRAFT_smci.m
%-----
clear all, close all
A0= [0 0 1.74 0.08 0.59;
0 -1.99 -13.41 -18.95 -3.6;
0 1 -1.74 -0.08 -0.59;
0 0 0 -20 0;
0 0 0 0 -20];
B0=[0 0;0 0;0 0;20 0;0 20];
H=[1 0 1 0 0;1 0 0 0 0];
A=[zeros(2,2) -H ;
zeros(5,2) A0];
B=[zeros(2,2); B0];
Gamma=diag([-0.9,-0.7]);
%-----
lambda=[-5.6 4.2 -1 -0.4 -0.7];
nocomp=1;
specpos=[zeros(2,5);[1 1 1 1 1;1 0 1 1 1;0 1 1 0 1];zeros(2,5)]
specent=[-ones(2,5);[0 0 1 0 1;1 -1 0 1 0;-1 1 0 -1 0];-ones(2,5)]
S=swfvpl(A,B,lambda,nocomp,specpos,specent);
SS=S(:,6:7)\S*0.05
F=(SS*B)\(SS*A)
eig(A-B*F)
%-----
[nn,mm]=size(B);
S1=SS(:,1:nn-mm);
S2=SS(:,nn-mm+1:nn);
Br=eye(nn-mm,mm);
B2=B(nn-mm+1:nn,:);
Lambda=S2*B2;
P2=diag([0.025,0.025]);
Phi=-20/0.025*P2;
Check=P2*Phi+Phi*P2
L=inv(Lambda)*(SS*A-Phi*SS)
%-----
%Sr=[-0.1448 0.0013;0.0196 0.1439]
Sr=zeros(2)
Lr=inv(Lambda)*(Phi*Sr+S1*Br)
Ldr=inv(Lambda)*Sr
Ln=0.1*inv(Lambda)
%-----
sim('AIRCRAFT_smci_2015a.mdl')
%-----
%eof
|
| SCILAB |
|
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} \dot{x}(t)=Ax(t)+Bu(t)\\ x(t)= \left[\begin{array}{ll} \theta & pitch\ angle\\ q & pitch\ rate\\ \alpha & angle\ of\ atack\\ \eta & elevator\ deflection\\ \delta & flap\ deflection \end{array}\right],\quad u(t)= \left[\begin{array}{ll} \eta_c & elevator\ command\\ \delta_c& flap\ comannd \end{array}\right]\\ A=\left[\begin{array}{rrrrr} 0 & 1 & 0 & 0 & 0\\ 0 &-1.99 & -13.41 & -18.95 & -3.60\\ 0 & 1 & -1.74 & -0.08 & -0.59\\ 0 & 0 & 0 & -20 & 0\\ 0 & 0 & 0 & 0 & -20 \end{array}\right],\quad B=\left[\begin{array}{rr} 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 20 & 0\\ 0 & 20 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e8e30c3e5083c206da3951e3e40e9cfb_l3.png)
![]() 行列の固有値は次のように求められます。
行列の固有値は次のように求められます。
![]() の代わりに、fligt path angle
の代わりに、fligt path angle ![]() を用いると、次式となります。
を用いると、次式となります。![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \begin{array}{l} \dot{x}(t)=Ax(t)+Bu(t)\\ x(t)= \left[\begin{array}{ll} \gamma=\theta-\alpha & fligt\ path\ angle\\ q & pitch\ rate\\ \alpha & angle\ of\ atack\\ \eta & elevator\ deflection\\ \delta & flap\ deflection \end{array}\right],\quad u(t)= \left[\begin{array}{ll} \eta_c & elevator\ command\\ \delta_c& flap\ comannd \end{array}\right]\\ A=\left[\begin{array}{rrrrr} 0 & 0 & 1.74 & 0.08 & 0.59\\ 0 &-1.99 & -13.41 & -18.95 & -3.60\\ 0 & 1 & -1.74 & -0.08 & -0.59\\ 0 & 0 & 0 & -20 & 0\\ 0 & 0 & 0 & 0 & -20 \end{array}\right],\quad B=\left[\begin{array}{rr} 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 20 & 0\\ 0 & 20 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b3ae110ebe0cc483c67a6db0b309e181_l3.png)
![]() とfligt path angle
とfligt path angle ![]() とすると、その出力方程式は次式のように与えられます。
とすると、その出力方程式は次式のように与えられます。![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} y(t)=Hx(t)\\ H= \left[\begin{array}{ccccc} 1 & 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c44cf07d269341a588b528f5aca4caf9_l3.png)
![]() とfligt path angle
とfligt path angle ![]() の間の非干渉化を達成し、独立して設定値に合せることです。
の間の非干渉化を達成し、独立して設定値に合せることです。
![Rendered by QuickLaTeX.com \displaystyle{(20)\quad { \boxed{\begin{array}{l} u(t)=u_\ell(t)+u_n(t)\\ u_\ell(t)=-\underbrace{(SB_E)^{-1}(SA_E-\Phi S)}_{L=L_{eq}+L_\Phi}\left[\begin{array}{c} x_r(t)\\ x(t) \end{array}\right]\\ -\underbrace{(SB_E)^{-1}(\Phi S_r+S_1B_r)}_{L_r} r(t) +\underbrace{(SB_E)^{-1}S_r}_{L_{\dot r}} \dot{r}(t)\\ u_n(t)=-\underbrace{(SB_E)^{-1}\rho(t,x)}_{L_n}\frac{P_2(s(t)-S_rr(t))}{||P_2(s(t)-S_rr(t))||} \end{array}}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-adc6bfdf1b50ea9ed3b1152bc4ee1729_l3.png)
![]() が望ましい固有値・固有ベクトルをもつように設計して、次式からスイッチング関数を決める行列
が望ましい固有値・固有ベクトルをもつように設計して、次式からスイッチング関数を決める行列![]() を決定します。
を決定します。![]()
![]() の望ましい固有値を
の望ましい固有値を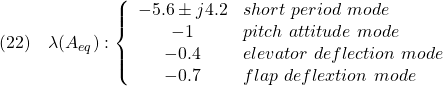
![Rendered by QuickLaTeX.com \displaystyle{(23)\quad {\tt specpos}= \left[\begin{array}{ccccc} 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\\hline 1 & 1 & 1 & 1 & 1\\ 1 & 0 & 1 & 1 & 1\\ 0 & 1 & 1 & 0 & 1\\\hline 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\ \end{array}\right],\quad {\tt specent}= \left[\begin{array}{rrrrr} -1 & -1 & -1 & -1 & -1\\ -1 & -1 & -1 & -1 & -1\\\hline 0 & 0 & 1 & 0 & 1\\ 1 & -1 & 0 & 1 & 0\\ -1 & 1 & 0 & -1 & 0\\\hline -1 & -1 & -1 & -1 & -1\\ -1 & -1 & -1 & -1 & -1\\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0c718bed933ebbd16e58b62392705e36_l3.png)
![]() を得ます。
を得ます。![]()
![]() などは次のように計算されます。
などは次のように計算されます。![]()
![]()
![]()
