LQ制御…Homework
[1] 可制御な制御対象
![]()
を安定化する状態フィードバック
![]()
の決定法を考えます。一つの方法は,閉ループ系
![]()
の時間応答に関する評価規範として,2次形式評価関数
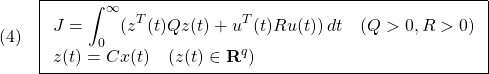
を設定し,これを最小化する問題を解くことです。ただし、![]() は可観測対とします。これによる状態フィードバックのゲイン行列
は可観測対とします。これによる状態フィードバックのゲイン行列![]() は,リッカチ方程式
は,リッカチ方程式
![]()
の解![]() を用いて,次式で与えられます。
を用いて,次式で与えられます。
![]()
この証明はNoteに示しています。
Note A52-1 行列による微分
いま、任意の行列![]() の
の![]() 要素を
要素を![]() で表すとき、スカラ関数
で表すとき、スカラ関数![]() を行列変数
を行列変数![]() の各要素で微分して得られる行列を
の各要素で微分して得られる行列を![]() で定義します。このとき、行列のトレースについて、次が成り立ちます。
で定義します。このとき、行列のトレースについて、次が成り立ちます。
![]()
![]()
![]()
![]()
実際、
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Note A52-2 LQ制御問題の解法
可制御かつ可観測な![]() 次系
次系
![]()
に対する状態フィードバック
![]()
による閉ループ系
![]()
に対して、評価関数
![]()
を最小化するように![]() を決める問題を考えます。
を決める問題を考えます。
閉ループ系における状態の振る舞いは次式で与えられます。
![]()
ここで、1次系の場合は初期状態は![]() であればよかったのですが、一般の場合はインパルス応答となるように
であればよかったのですが、一般の場合はインパルス応答となるように![]() の列ベクトル
の列ベクトル![]() を考えます。各インパルス応答
を考えます。各インパルス応答
![]()
に対する評価関数![]() の総和は
の総和は
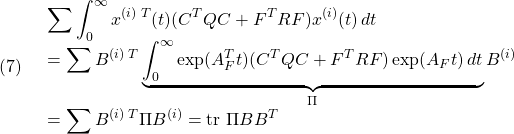
と書けます。いま![]() をラグランジュの未定定数として
をラグランジュの未定定数として
![]()
を最小化する問題を考えます。ここで、制約条件は、リャプノフ方程式と呼ばれる
![]()
ですが、![]() は
は![]() が安定行列を意味することに注意します。
が安定行列を意味することに注意します。
そこで、必要条件として次を得ます。
![]()
![]()
![]()
ここで、第2式から得られる![]() を第3式に代入して
を第3式に代入して
![]()
すなわち、リッカチ方程式と呼ばれる![]() の行列方程式
の行列方程式
![]()
を得ます。これから![]() を求めて、
を求めて、![]() は
は
![]()
のように得られます。このような制御方式をLQ制御と呼びます。
一方、十分性の議論は次のように行われます。まず、被積分項は次のように表すことができます。
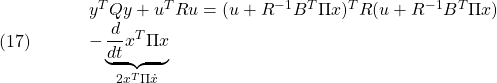
実際、右辺に![]() を代入し、リッカチ方程式を用いると
を代入し、リッカチ方程式を用いると
![]()
したがって、上記の両辺を積分して
![]()
を得ます。ここで、![]() を前提とするので
を前提とするので
![]()
を得ます。これから![]() が評価関数を最小化することが分かります。
が評価関数を最小化することが分かります。