スイッチング関数(1)
[1] 状態方程式とスイッチング関数は次の標準形をとるように座標変換されていると仮定します。
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot x(t)} = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a4c8217b8c641b28c9d2c724fc2462cb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} \ (M=S_2^{-1}S_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0639c7053096db5f35e066d8fec1086a_l3.png)
これに対して、座標変換
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ -S_2^{-1}S_1 & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d6ab22ac2ca3b874b7f25f131d7dadba_l3.png)
を行って、次式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{\bar{x}}(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ \bar{A}_{21} & \bar{A}_{22}\\ \end{array}\right] }_{\bar{A}=T_s A T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} + \underbrace{ \left[\begin{array}{c} 0\\ \bar{B}_2 \end{array}\right] }_{\bar{B}=T_sB} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c151e790bb46588ffe833fc57ad6301b_l3.png)
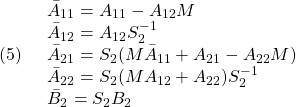
ここで、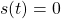 、すなわち、状態が超平面内に拘束されているとすると
、すなわち、状態が超平面内に拘束されているとすると
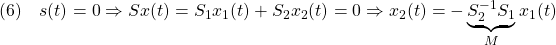
となって、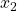 の振る舞いは
の振る舞いは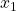 によって決まります。一方、
によって決まります。一方、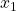 の振る舞いは
の振る舞いは
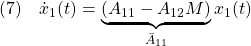
によって決まります。これは
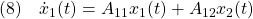
に対する安定化状態フィードバック
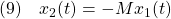
による閉ループ系とみなすことができます。
したがって、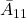 が安定行列となるようにスイッチング関数を選ぶためには、(8)に対する状態フィードバックによる安定化問題を解けばよいことが分かります。
が安定行列となるようにスイッチング関数を選ぶためには、(8)に対する状態フィードバックによる安定化問題を解けばよいことが分かります。
[2] そこで、次の2次形式評価関数を最小にするように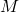 を決定する方法が提案されています。
を決定する方法が提案されています。
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \boxed{J=\int_0^\infty \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right]^T }_{x^T(t)} \underbrace{ \left[\begin{array}{cc} Q_{11} & Q_{12} \\ Q_{21} & Q_{22} \end{array}\right] }_{Q} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} dt} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-720950a912af5f2005feadc55eef2316_l3.png)
これは、恒等式
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \left[\begin{array}{cc} Q_{11} & Q_{12} \\ Q_{21} & Q_{22} \end{array}\right]}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b918b1aa48174b4ca0725d531e0a3a1f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ =\left[\begin{array}{cc} I & Q_{12}Q_{22}^{-1} \\ 0 & I \end{array}\right] \left[\begin{array}{cc} Q_{11}-Q_{12}Q_{22}^{-1}Q_{21} & 0 \\ 0 & Q_{22} \end{array}\right] \left[\begin{array}{cc} I & 0 \\ Q_{22}^{-1}Q_{21} & I \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a05e1a70ec910d8db925c9e9cdfd9223_l3.png)
を用いて
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right]^T \left[\begin{array}{cc} Q_{11} & Q_{12} \\ Q_{21} & Q_{22} \end{array}\right] \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] =\left[\begin{array}{c} x_1(t)\\ Q_{12}Q_{22}^{-1}x_1(t)+x_2(t) \end{array}\right]^T }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b67f7b3891ae54055fefcef1f1c4c7e0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \times \left[\begin{array}{cc} Q_{11}-Q_{12}Q_{22}^{-1}Q_{21} & 0 \\ 0 & Q_{22} \end{array}\right] \left[\begin{array}{c} x_1(t)\\ Q_{12}Q_{22}^{-1}x_1(t)+x_2(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-49d660ff1a02cfdda090585ad3c36ad5_l3.png)
より
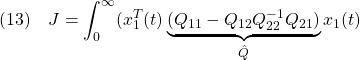
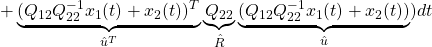
と書けます。ここで、(8)と(6)をそれぞれ
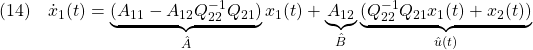
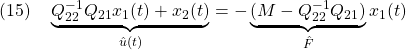
と書き直してみますと、次のような最適化制御問題の定式化ができていることがわかります。すなわち
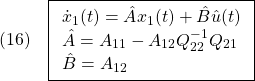
を2次系式評価関数
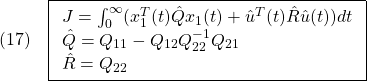
を最小にするように
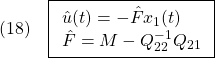
を求める問題です。この解は、リッカチ方程式
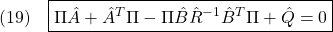
を解いて
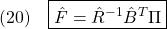
を求め、次式から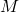 を決めればよいことがわかります。
を決めればよいことがわかります。
演習C31…Flipped Classroom
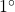 スイッチング関数決定プログラムswflqrを用いて、図1の台車駆動型倒立振子を安定化する次のSMC則を求めよ。
スイッチング関数決定プログラムswflqrを用いて、図1の台車駆動型倒立振子を安定化する次のSMC則を求めよ。
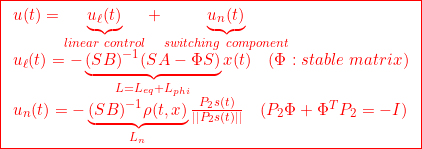
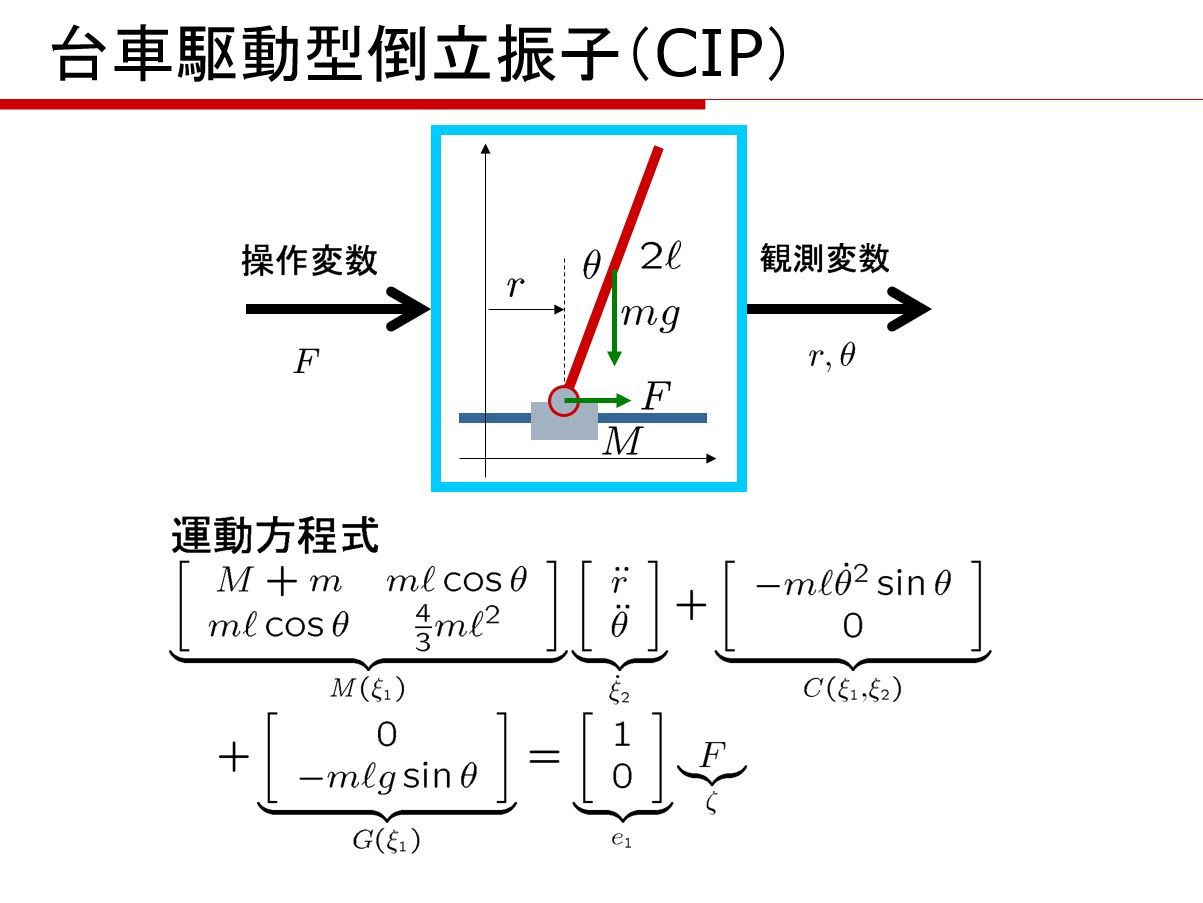
図1 台車駆動型倒立振子
| MATLAB |
%cCIP_smc1.m
%-----
clear all, close all
global mc m ell g th0
mc=1; m=0.1; ell=0.2; g=9.8;
ths=0; %input('ths = <0,180> ')/180*pi;
th0=3/180*pi; %input('th(0) = <0,180> ')/180*pi;
%-----
A=[zeros(2,2) eye(2);zeros(2,4)];
A(3,1)=0;
A(3,2)=-3*m*g/(m+4*mc);
A(4,1)=0;
A(4,2)=3*(m+mc)*g/((m+4*mc)*ell);
B=zeros(4,1);
B(3)=4/(m+4*mc);
B(4)=-3/((m+4*mc)*ell);
C=diag([100 180/pi])*eye(2,4);
%-----
Mr=0.5; Mth=3/180*pi;
Tc=1; Tpen=0.25*2*pi*sqrt(2*ell/g);
Q=diag([1/Mr^2,1/Mth^2,Tc^2/Mr^2,Tpen^2/Mth^2]);
S=swflqr(A,B,Q)
%-----
Phi=-0.1;
P2=0.5*inv(-Phi);
Check=P2*Phi+Phi*P2
P2S=P2*S;
Leq=inv(S*B)*S*A;
LPhi=-inv(S*B)*Phi*S;
L=Leq+LPhi;
rho=1.5;
Ln=inv(S*B)*rho;
%-----
x0=[0;th0;0;0];
sim('CIP_smc_2015a.mdl')
%-----
%eof
|

Note C31 スイッチング関数決定プログラム1
Edwards and Spurgeon によって、(19)、(20)、(21)から、スイッチング関数の行列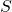 を求めるプログラムswflqrが開発されています。
を求めるプログラムswflqrが開発されています。
| MATLAB |
%test_swflqr.m
%-----
clear all, close all
A=[0 1 0;
0 0 1;
0 0 0];
B=[0;
0;
1];
%-----
Q=eye(3,3);
S=swflqr(A,B,Q)
%-----
%eof
|
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot x(t)} = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a4c8217b8c641b28c9d2c724fc2462cb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} \ (M=S_2^{-1}S_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0639c7053096db5f35e066d8fec1086a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ -S_2^{-1}S_1 & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d6ab22ac2ca3b874b7f25f131d7dadba_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{\bar{x}}(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ \bar{A}_{21} & \bar{A}_{22}\\ \end{array}\right] }_{\bar{A}=T_s A T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} + \underbrace{ \left[\begin{array}{c} 0\\ \bar{B}_2 \end{array}\right] }_{\bar{B}=T_sB} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c151e790bb46588ffe833fc57ad6301b_l3.png)
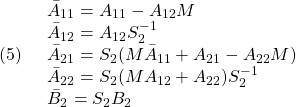
![]() 、すなわち、状態が超平面内に拘束されているとすると
、すなわち、状態が超平面内に拘束されているとすると![]()
![]() の振る舞いは
の振る舞いは![]() によって決まります。一方、
によって決まります。一方、![]() の振る舞いは
の振る舞いは![]()
![]()
![]()
![]() が安定行列となるようにスイッチング関数を選ぶためには、(8)に対する状態フィードバックによる安定化問題を解けばよいことが分かります。
が安定行列となるようにスイッチング関数を選ぶためには、(8)に対する状態フィードバックによる安定化問題を解けばよいことが分かります。![]() を決定する方法が提案されています。
を決定する方法が提案されています。![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \boxed{J=\int_0^\infty \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right]^T }_{x^T(t)} \underbrace{ \left[\begin{array}{cc} Q_{11} & Q_{12} \\ Q_{21} & Q_{22} \end{array}\right] }_{Q} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} dt} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-720950a912af5f2005feadc55eef2316_l3.png)
![]()
![]()
![]()
![]()
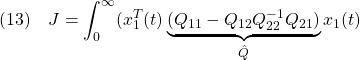
![]()
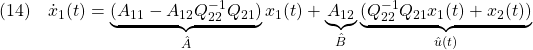
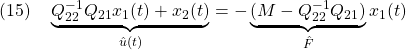
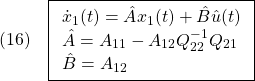
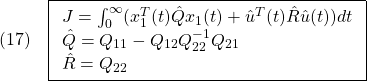
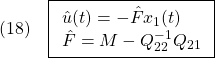
![]()
![]()
![]() を決めればよいことがわかります。
を決めればよいことがわかります。![]()
![]() スイッチング関数決定プログラムswflqrを用いて、図1の台車駆動型倒立振子を安定化する次のSMC則を求めよ。
スイッチング関数決定プログラムswflqrを用いて、図1の台車駆動型倒立振子を安定化する次のSMC則を求めよ。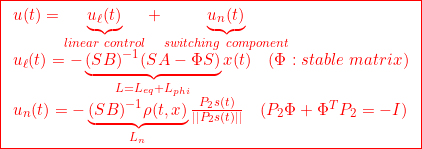


![]() を求めるプログラムswflqrが開発されています。
を求めるプログラムswflqrが開発されています。