リャプノフの安定定理
非線形システム理論に関する文献:
Hassan K.Khalil: Nonlinear Systems, 3rd ed., Prentice Hall, 2002
から次の定理(Theorem 4.1, p.114)を引用します。
|
リャプノフの安定定理 状態方程式
に対して、その平衡状態
このとき
ならば、平衡状態
ならば、平衡状態 |
すなわち、(2)と(4)を満足するリャプノフ関数![]() の存在を示して(発見して)、非線形系(1)の漸近安定性を示すことができます。
の存在を示して(発見して)、非線形系(1)の漸近安定性を示すことができます。
2次安定性
非線形系(1)に対してリャプノフ関数
![]()
を考えます。これを微分して(1)を用いると((1)の解に沿って微分して)
![]()
となります。このとき2次安定とは
![]()
が成り立つことを言います。これは、次式を示すことができ、漸近安定性を意味するからです。
![]()
ただし
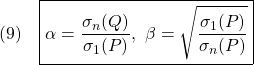
以下では、これを導出します。
●予備知識として、任意の対称行列![]() に対して、特異値(固有値に等しい)を
に対して、特異値(固有値に等しい)を
![]()
と表記し、また任意の![]() に対して
に対して
![]()
および
![]()
が成り立つこと使います。
●そこで
![]()
に注意して、次式を得ます。
![]()
これから
![]()
ここで
![]()
に注意して
![]()
すなわち
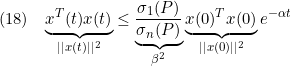
を得ます。これから(8)が成り立ちます。なお一般には
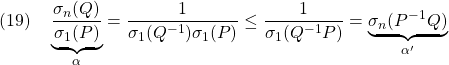
ですが、![]() と
と![]() を対角行列に選ぶときは等号が成り立ち、(8)において
を対角行列に選ぶときは等号が成り立ち、(8)において![]() ではなく
ではなく![]() を用いることができます。もう少し詳しくは、対称行列
を用いることができます。もう少し詳しくは、対称行列![]() と
と![]() が可換(
が可換(![]() )で、同時対角化可能(
)で、同時対角化可能(![]() と
と![]() を対角行列とする
を対角行列とする![]() が存在)の場合には等号が成り立ち、(8)において
が存在)の場合には等号が成り立ち、(8)において![]() ではなく
ではなく![]() を用いることができます。
を用いることができます。
Note C11 (11),(12)の導出
●任意の正定行列![]() (サイズ
(サイズ![]() )に対して、次の特異値分解を考えます。
)に対して、次の特異値分解を考えます。
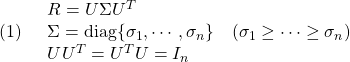
ここで、![]() は対称行列なので固有値は実数、しかも正定なのでそれらはすべて正であること、したがって特異値
は対称行列なので固有値は実数、しかも正定なのでそれらはすべて正であること、したがって特異値![]() は
は![]() の最大固有値、特異値
の最大固有値、特異値![]() は
は![]() の最小固有値であることに注意してください。このとき、
の最小固有値であることに注意してください。このとき、![]() を満たす
を満たす![]() の平方根行列は
の平方根行列は
![]()
で与えられます。また、![]() の逆行列は
の逆行列は
![]()
のように表されます。これから(12)は自明です。
いま、![]() を用いて線形写像
を用いて線形写像![]() を考えると、これは3つの線形写像に分解されます。
を考えると、これは3つの線形写像に分解されます。
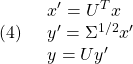
任意の![]() 次元ベクトル
次元ベクトル![]() のノルムとして、次の2ノルムを考えます。
のノルムとして、次の2ノルムを考えます。
![]()
このとき、次が成り立ちます。
![]()
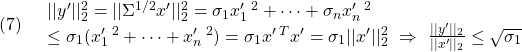
![]()
すなわち
![]()
一方
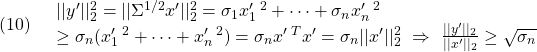
より、次式が成り立ちます。
![]()
したがって、(7)と合わせて、次式を得ます。
![]()
これを2乗して次が得られます。
![]()
すなわち(11)が導出されました。