D制約LMI
[1] 次の命題が成り立ちます。
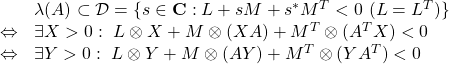 |
●十分性(![]() )は、クロネッカ積の公式
)は、クロネッカ積の公式![]() を用いて、
を用いて、![]() (
(![]() )のとき
)のとき
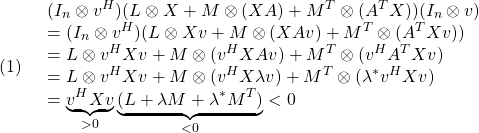
が成り立つことから出ます。
●必要性(![]() )を示すために、まず
)を示すために、まず![]() は対角化可能とします。このとき
は対角化可能とします。このとき
![]()
ならば、明らかにこれらをブロック対角にもたせた次式が成り立ちます。
![]()
一般に、![]() が対角化可能ではないときは、そのジョルダン分解を
が対角化可能ではないときは、そのジョルダン分解を
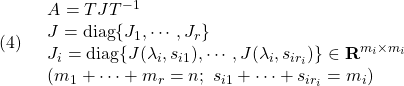
ただし、ジョルダン細胞を
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad J(\lambda,k)=\left[\begin{array}{cccc} \lambda & 1 & & 0\\ 0 & \lambda & \ddots & \\ \vdots & \ddots & \ddots & 1 \\ 0 & \cdots & 0 & \lambda \end{array}\right]\in{\rm\bf R}^{k\times k} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ab96841e90e0d9dd55c8e1fbe6d37b58_l3.png)
とします。いま
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad T_\epsilon=\left[\begin{array}{cccc} 1 & 0 & \cdots & 0\\ 0 & \frac{1}{\epsilon} & \ddots & \vdots\\ \vdots & \ddots & \ddots & 0\\ 0 & \cdots & 0 & \frac{1}{\epsilon^{k-1}} \end{array}\right],\ T_\epsilon^{-1}=\left[\begin{array}{cccc} 1 & 0 & \cdots & 0\\ 0 & {\epsilon} & \ddots & \vdots\\ \vdots & \ddots & \ddots & 0\\ 0 & \cdots & 0 & {\epsilon^{k-1}} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-105301a3a42f7ab0eb9750acac26e2ce_l3.png)
を用いて
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} T_\epsilon J(\lambda,k)T_\epsilon^{-1}\\ =T_\epsilon \left[\begin{array}{cccc} \lambda & 1 & & 0\\ 0 & \lambda & \ddots & \\ \vdots & \ddots & \ddots & 1 \\ 0 & \cdots & 0 & \lambda \end{array}\right] \left[\begin{array}{cccc} 1 & 0 & \cdots & 0\\ 0 & {\epsilon} & \ddots & \vdots\\ \vdots & \ddots & \ddots & 0\\ 0 & \cdots & 0 & {\epsilon^{k-1}} \end{array}\right]\\ =\left[\begin{array}{cccc} 1 & 0 & \cdots & 0\\ 0 & \frac{1}{\epsilon} & \ddots & \vdots\\ \vdots & \ddots & \ddots & 0\\ 0 & \cdots & 0 & \frac{1}{\epsilon^{k-1}} \end{array}\right] \left[\begin{array}{cccc} \lambda & \epsilon & & 0\\ 0 & \lambda\epsilon & \ddots & \\ \vdots & \ddots & \ddots & \epsilon^{k-1} \\ 0 & \cdots & 0 & \lambda\epsilon^{k-1} \end{array}\right]\\ =\left[\begin{array}{cccc} \lambda & \epsilon & & 0\\ 0 & \lambda & \ddots & \\ \vdots & \ddots & \ddots & \epsilon \\ 0 & \cdots & 0 & \lambda \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-517f70ee4d5a06e559e5f4be6fd4bd76_l3.png)
を得ます。したがって、![]() の各ジョルダン細胞に対する
の各ジョルダン細胞に対する![]() をブロック対角に持たせた
をブロック対角に持たせた![]() を用いて
を用いて
![]()
は十分小さな![]() に対して対角行列となります。したがって、(3)と同様に次式を得ます。
に対して対角行列となります。したがって、(3)と同様に次式を得ます。
![]()
これから、![]() とおき、
とおき、![]() (
(![]() )を用いて
)を用いて
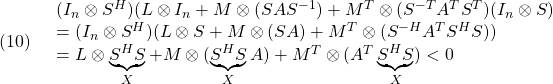
が成り立ち、必要性が示されたことになります。