セクタ制約LMI | 制御系CAD

セクタ制約LMI…Homework

[1] 次の領域 ${\cal D}_3$ を考えます。

図1 領域 ${\cal D}_3$

このとき、次の命題が成り立ちます。

$\displaystyle{(12)\quad \begin{array}{lll} &&\lambda(A)\subset {\cal D}_3=\{s=x+jy\in{\rm\bf C}:\\ && \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right]s + \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right]^Ts^* <0 \}\nonumber\\ &&\Leftrightarrow \exists X>0:\ \left[\begin{array}{cc} \sin\theta(XA+A^TX) & \cos\theta(XA-A^TX) \\ -\cos\theta(XA-A^TX) & \sin\theta(XA+A^TX) \end{array}\right] <0 \nonumber\\ &&\Leftrightarrow \exists Y>0:\ \left[\begin{array}{cc} \sin\theta(AY+YA^T) & \cos\theta(AY-YA^T) \\ -\cos\theta(AY-YA^T) & \sin\theta(AY+YA^T) \end{array}\right] <0\nonumber \end{array} }$

実際、まず領域 ${\cal D}_3$ が上図を表すことは、次のように確かめられます。

$\displaystyle{(13)\quad \begin{array}{lll} && \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right]s + \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right]^Ts^* <0 \nonumber\\ &\Leftrightarrow& \left[\begin{array}{cc} (s+s^*)\sin\theta & (s-s^*)\cos\theta \\ -(s-s^*)\cos\theta & (s+s^*)\sin\theta \end{array}\right] <0 \nonumber\\ &\Leftrightarrow& \left[\begin{array}{cc} 2x\sin\theta & 2jy\cos\theta \\ -2jy\cos\theta & 2x\sin\theta \end{array}\right] <0 \nonumber\\ &\Leftrightarrow& x\sin\theta-jy\cos\theta\frac{1}{x\sin\theta}(-j)y\cos\theta<0,\ x\sin\theta<0 \nonumber\\ &\Leftrightarrow& x^2\sin^2\theta-y^2\cos^2\theta>0,\ x<0 \nonumber\\ &\Leftrightarrow& \tan\theta>\frac{|y|}{-x},\ x<0 \nonumber \end{array} }$

次に、十分性は、 $Av=\lambda v$ とすると、次のように確かめられます。

$\displaystyle{(14) \begin{array}{lll} &&\left[\begin{array}{cc} v^{*T} & 0^{T}\\ 0^{T} & v^{*T} \end{array}\right] \left[\begin{array}{cc} \sin\theta(XA+A^TX) & \cos\theta(XA-A^TX) \\ -\cos\theta(XA-A^TX) & \sin\theta(XA+A^TX) \end{array}\right] \left[\begin{array}{cc} v & 0\\ 0 & v \end{array}\right] \nonumber\\ &=& \left[\begin{array}{cc} \sin\theta(v^{*T}X(\lambda v)+(\lambda^*v^{*T})Xv) & \cos\theta(v^{*T}X(\lambda v)-(\lambda^*v^{*T})Xv) \\ -\cos\theta(v^{*T}X(\lambda v)-(\lambda^*v^{*T})Xv) & \sin\theta(v^{*T}X(\lambda v)+(\lambda^*v^{*T})Xv) \end{array}\right] \nonumber\\ &=& \underbrace{ \left[\begin{array}{cc} (\lambda+\lambda^*)\sin\theta & (\lambda-\lambda^*)\cos\theta \\ -(\lambda-\lambda^*)\cos\theta & (\lambda+\lambda^*)\sin\theta \end{array}\right] }_{<0} \underbrace{v^{*T}Xv}_{>0}<0 \nonumber \end{array} }$

さらに、 $y_1=Xx_1,y_2=Xx_2$ とおくと、次が成り立ちます。

$\displaystyle{(15) \begin{array}{lll} && \left[\begin{array}{cc} x_1^T & x_2^T \end{array}\right] \left[\begin{array}{cc} \sin\theta(XA+A^TX) & \cos\theta(XA-A^TX) \\ -\cos\theta(XA-A^TX) & \sin\theta(XA+A^TX) \end{array}\right] \left[\begin{array}{c} x_1\\ x_2 \end{array}\right] <0 \nonumber\\ &&\quad (\forall x_1,x_2\ne0)\nonumber\\ &\Leftrightarrow& \left[\begin{array}{cc} x_1^TX & x_2^TX \end{array}\right]\\ && \left[\begin{array}{cc} \sin\theta(AX^{-1}+X^{-1}A^T) & \cos\theta(AX^{-1}-X^{-1}A^T) \\ -\cos\theta(AX^{-1}-X^{-1}A^T) & \sin\theta(AX^{-1}+X^{-1}A^T) \end{array}\right] \left[\begin{array}{c} Xx_1\\ Xx_2 \end{array}\right] <0 \nonumber\\ &\Leftrightarrow& \left[\begin{array}{cc} y_1^T & y_2^T \end{array}\right] \left[\begin{array}{cc} \sin\theta(AY+YA^T) & \cos\theta(AY-YA^T) \\ -\cos\theta(AY-YA^T) & \sin\theta(AY+YA^T) \end{array}\right] \left[\begin{array}{c} y_1\\ y_2 \end{array}\right] <0 \nonumber\\ &&\quad (\forall y_1,y_2\ne0)\nonumber \end{array} }$

必要性については、あとで述べます。

演習B13-1…Flipped Classroom
$1^\circ$ セクタ制約を調べる次のコードを説明せよ。

MATLAB

%ana_lmi3.m
%-----
 clear all, close all
 A=[0 1;-2 -2]; n=2;
%-----
 setlmis([]);  
 X=lmivar(1,[n 1]);  
%-----
 th=pi/6; sth=sin(th); cth=cos(th); 
 lmi1=newlmi;  
 lmiterm([lmi1 1 1 X],1,sth*A,'s'); %#1:sth*(X*A+A'*X) 
 lmiterm([lmi1 1 2 X],1,cth*A);     %#1:cth*X*A 
 lmiterm([lmi1 1 2 X],-cth*A',1);   %#1:-cth*A'*X 
 lmiterm([lmi1 2 2 X],1,sth*A,'s'); %#1:sth*(X*A+A'*X) 
%-----
 lmi2=newlmi;  
 lmiterm([-lmi2 1 1 X],1,1);        %#2:X  
%-----
 LMIs=getlmis;  
 [tmin,xfeas]=feasp(LMIs);  
 X=dec2mat(LMIs,xfeas,X)  
%-----
%eof

[2] 次の領域 ${\cal D}={\cal D}_1\cup{\cal D}_2\cup{\cal D}_3$ を考えます。

図2 領域 ${\cal D}={\cal D}_1\cup{\cal D}_2\cup{\cal D}_3$

このとき、次の命題が成り立ちます。

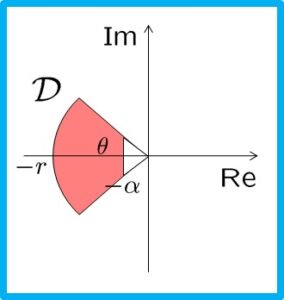
$\displaystyle{(16)\quad \begin{array}{lll} && \lambda(A)\subset {\cal D}={\cal D}_1\cap{\cal D}_2\cap{\cal D}_3\nonumber\\ &&\Leftrightarrow \exists X>0:\nonumber\\ & & \left\{\begin{array}{l} 2\alpha X+XA+A^TX<0 \\ \left[\begin{array}{cc} -rX & XA \\ A^TX & -rX \end{array}\right]<0 \\ \left[\begin{array}{cc} \sin\theta(XA+A^TX) & \cos\theta(XA-A^TX) \\ -\cos\theta(XA-A^TX) & \sin\theta(XA+A^TX) \end{array}\right] <0 \end{array}\right.\nonumber\\ &&\Leftrightarrow \exists Y>0:\nonumber\\ & & \left\{\begin{array}{l} 2\alpha Y+AY+YA^T<0 \\ \left[\begin{array}{cc} -rY & AY \\ YA^T & -rY \end{array}\right]<0 \\ \left[\begin{array}{cc} \sin\theta(AY+YA^T) & \cos\theta(AY-YA^T) \\ -\cos\theta(AY-YA^T) & \sin\theta(AY+YA^T) \end{array}\right] <0 \end{array}\right.\nonumber \end{array} }$

演習B13-2…Flipped Classroom
$1^\circ$ 次を参考にして、 ${\cal D}$ 制約を満たす状態FBを求める関数を作成せよ。

MATLAB

%ana_lmi4.m 
%-----
 clear all, close all
 A=[0 1;-2 -3]; n=2;
%-----
 setlmis([]);  
 X=lmivar(1,[n 1]);  
%-----
 alpha=0.5;
 lmi1=newlmi; 
 lmiterm([lmi1 1 1 X],1,A,'s');     %#1:XA+A'*X   
 lmiterm([lmi1,1,1,X],2*alpha,1);   %#1:2*alpha*X
%
 q=0; r=3;
 lmi2=newlmi; 
 lmiterm([lmi2 1 1 X],-r,1);        %#2:   
 lmiterm([lmi2 1 2 X],1,A);         %#2:2*alpha*X  
 lmiterm([lmi2 2 2 X],-r,1);        %#2: 
%
 th=pi/4; sth=sin(th); cth=cos(th); 
 lmi3=newlmi;  
 lmiterm([lmi3 1 1 X],1,sth*A,'s'); %#3:sth*(X*A+A'*X) 
 lmiterm([lmi3 1 2 X],1,cth*A);     %#3:cth*X*A 
 lmiterm([lmi3 1 2 X],-cth*A',1);   %#3:-cth*A'*X 
 lmiterm([lmi3 2 2 X],1,sth*A,'s'); %#3:sth*(X*A+A'*X) 
%
 lmi4=newlmi;  
 lmiterm([-lmi4 1 1 X],1,1);        %#4:X  
%----- 
 LMIs=getlmis;  
 [tmin,xfeas]=feasp(LMIs);  
 X=dec2mat(LMIs,xfeas,X)
%-----
%eof