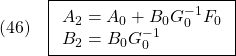可制御正準形 | 制御系CAD

可制御正準形…Homework

[0]　 $n$ 次系 $\dot{x}=Ax+Bu\ (x\in{\rm\bf R}^n,u\in{\rm\bf R}^m)$ に対して、次を仮定します。

$\displaystyle{(1)\quad {\rm rank}\left[\begin{array}{cccc} B & AB &\cdots & A^{n-1}B \end{array}\right]=n }$

このとき、以下では、２つの座標変換を続けて行います。

$\displaystyle{(2)\quad x'=T_1x\ \Rightarrow\ \dot{x}'=A_1x'+B_1u }$

$\displaystyle{(3)\quad x''=T_2x'\ \Rightarrow\ \dot{x}''=A_2x''+B_2u }$

そして、 $A_2-B_2F_2$ の特性多項式を任意に設定するための $F_2$ の１つを示します。

[1]　１入力系の場合を考えます。 $A$ の特性多項式を

$\displaystyle{(4)\quad \det(\lambda I_n-A)=\lambda^n+a_1\lambda^{n-1}+\cdots+a_n }$

としますと、ケーリ―・ハミルトンの定理より

$\displaystyle{(5)\quad A^n+a_1A^{n-1}+\cdots+a_nI_n=0 }$

が成り立ちます。これから

$\displaystyle{(6)\quad A^nB=-a_nB-\cdots-a_1A^{n-1}B }$

を得ます。これに基づいて

$\displaystyle{(7)\quad \begin{array}{l} A \underbrace{ \left[\begin{array}{cccc} B & AB &\cdots & A^{n-1}B \end{array}\right] }_{T_1^{-1}}\\ = \underbrace{ \left[\begin{array}{cccc} B & AB &\cdots & A^{n-1}B \end{array}\right] }_{T_1^{-1}} \underbrace{ \left[\begin{array}{ccccc} 0 & \cdots & 0 & -a_n \\ 1 & \cdots & 0 & -a_{n-1} \\ \vdots & \ddots & \vdots &\vdots\\ 0 & \cdots & 1 & -a_1 \end{array}\right] }_{A_1} \end{array} }$

を得ます。これから次の第１番目の正準形が定義されます。

$\displaystyle{(8)\quad \boxed{ \begin{array}{l} A_1=T_1AT_1^{-1}= \left[\begin{array}{ccccc} 0 & \cdots & 0 & -a_n \\ 1 & \cdots & 0 & -a_{n-1} \\ \vdots & \ddots & \vdots &\vdots\\ 0 & \cdots & 1 & -a_1 \end{array}\right]\\ B_1=T_1B= \left[\begin{array}{cc} 1 \\ 0\\ \vdots\\ 0 \end{array}\right] \end{array}} }$

さて、次式が成り立ちます。

$\displaystyle{(9)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{ccccc} 0 & \cdots & 0 & -a_n \\ 1 & \cdots & 0 & -a_{n-1} \\ \vdots & \ddots & \vdots &\vdots\\ 0 & \cdots & 1 & -a_1 \end{array}\right] }_{A_1} \underbrace{ \left[\begin{array}{ccccc} a_{n-1} & a_{n-2} & \cdots & a_1 & 1 \\ a_{n-2} & a_{n-3} & \cdots & 1 & 0 \\ \vdots & \vdots & \cdots & \vdots & \vdots \\ a_1 & 1 & \cdots & 0 & 0 \\ 1 & 0 & \cdots & 0 & 0 \end{array}\right] }_{T_2^{-1}}\\ =\underbrace{ \left[\begin{array}{ccccc} a_{n-1} & a_{n-2} & \cdots & a_1 & 1 \\ a_{n-2} & a_{n-3} & \cdots & 1 & 0 \\ \vdots & \vdots & \cdots & \vdots & \vdots \\ a_1 & 1 & \cdots & 0 & 0 \\ 1 & 0 & \cdots & 0 & 0 \end{array}\right] }_{T_2^{-1}} \underbrace{ \left[\begin{array}{ccccc} 0 & 1 & \cdots & 0\\ \vdots & \vdots & \cdots & \vdots \\ 0 & 0 & \cdots & 1\\ -a_n & -a_{n-1} & \cdots & -a_1 \end{array}\right] }_{A_2} \end{array} }$

実際、 $n=2$ のときは、次のように示されます。

$\displaystyle{(10)\quad {\rm LHS}=\left[\begin{array}{cc} 0 & -a_2 \\ 1 & -a_1 \end{array}\right] \left[\begin{array}{cc} a_1 & 1 \\ 1 & 0 \end{array}\right] = \left[\begin{array}{cc} -a_2 & 0 \\ 0 & 1 \end{array}\right] }$

$\displaystyle{(11)\quad {\rm RHS}= \left[\begin{array}{cc} a_1 & 1 \\ 1 & 0 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \\ -a_2 & -a_1 \end{array}\right] = \left[\begin{array}{cc} -a_2 & 0 \\ 0 & 1 \end{array}\right] }$

一般には、次のように示されます。

$\displaystyle{(12)\quad \begin{array}{l} {\rm LHS}=\\ \left[\begin{array}{cc} 0_{1\times n-1} & -a_n \\ I_{n-1\times n-1} & \left[\begin{array}{c} -a_{n-1} \\ \vdots\\ -a_1 \end{array}\right] \end{array}\right] \left[\begin{array}{cccc|c} a_{n-1} & a_{n-2} & \cdots & a_1 & 1 \\ a_{n-2} & a_{n-3} & \cdots & 1 & 0 \\ \vdots & \vdots & \cdots & \vdots & \vdots \\ a_1 & 1 & \cdots & 0 & 0 \\\hline 1 & 0 & \cdots & 0 & 0 \end{array}\right]\\ = \left[\begin{array}{cccc|c} -a_n & 0 & \cdots & 0 & 0 \\\hline 0 & a_{n-2} & \cdots & a_1 & 1 \\ 0 & a_{n-3} & \cdots & 1 & 0 \\ \vdots & \vdots & \cdots & \vdots & \vdots \\ 0 & 1 & \cdots & 0 & 0 \end{array}\right] \end{array} }$

$\displaystyle{(13)\quad \begin{array}{l} {\rm RHS}=\\ \left[\begin{array}{cccc|c} a_{n-1} & a_{n-2} & \cdots & a_1 & 1 \\ a_{n-2} & a_{n-3} & \cdots & 1 & 0 \\ \vdots & \vdots & \cdots & \vdots & \vdots \\ a_1 & 1 & \cdots & 0 & 0 \\\hline 1 & 0 & \cdots & 0 & 0 \end{array}\right] \left[\begin{array}{cc} 0_{n-1\times 1} & I_{n-1\times n-1} \\ -a_n & \left[\begin{array}{ccc} -a_{n-1} & \cdots & -a_1 \end{array}\right] \end{array}\right]\\ = \left[\begin{array}{c|cccc} -a_n & 0 & \cdots & 0 & 0 \\ 0 & a_{n-2} & \cdots & a_1 & 1 \\ 0 & a_{n-3} & \cdots & 1 & 0 \\ \vdots & \vdots & \cdots & \vdots & \vdots \\\hline 0 & 1 & \cdots & 0 & 0 \end{array}\right] \end{array} }$

上の関係式(9)に基づいて、次の第２番目の正準形が定義されます。

$\displaystyle{(14)\quad \boxed{ \begin{array}{l} A_2=T_2A_1T_2^{-1}= \left[\begin{array}{ccccc} 0 & 1 & \cdots & 0\\ \vdots & \vdots & \cdots & \vdots \\ 0 & 0 & \cdots & 1\\ -a_n & -a_{n-1} & \cdots & -a_1 \end{array}\right]\\ B_2=T_2B_1= \left[\begin{array}{cc} 0 \\ \vdots\\ 0\\ 1 \end{array}\right] \end{array}} }$

したがって、 $A_2-B_2F_2$ の特性多項式を

$\displaystyle{(15)\quad \det(\lambda I_n-A_2+B_2F_2)=\lambda^n+a_1'\lambda^{n-1}+\cdots+a_n' }$

とする $F_2$ は、次式で与えられます。

$\displaystyle{(16)\quad F_2=\left[\begin{array}{ccccc} a_n'-a_n & a_{n-1}'-a_{n-1} & \cdots & a_1'-a_1 \end{array}\right] }$

[2]　多入力系の場合を数値例を用いて説明します。

$\displaystyle{(17)\quad \begin{array}{l} A= \left[\begin{array}{ccc} 0 & 7 & 4 \\ 1 & -1 & -2\\ 0 & 3 & 1 \end{array}\right],\ B= \left[\begin{array}{cc} 1 & 0 \\ 0 & 0 \\ 0 & 1 \end{array}\right] \end{array} }$

に対して、可制御性は

$\displaystyle{(18)\quad \begin{array}{l} {\rm rank} \left[\begin{array}{ccc} B & AB & A^2B \end{array}\right]= {\rm rank}\ \left[\begin{array}{cc|cc|cc} 1 & 0 & 0 & 4 & 7 & -10\\ 0 & 0 & 1 & -2 & -1 & 4\\ 0 & 1 & 0 & 1 & 3 & 5 \end{array}\right]=3 \end{array} }$

となって成立しています。そこで $B$ の第１列ベクトルと第２ベクトルをそれぞれ $B_1$ と $B_2$ で表すとき、

$\displaystyle{(19)\quad \begin{array}{l} B_1,B_2,AB_1,AB_2,A^2B_1,A^2B_2 \end{array} }$

の順にベクトルの１次独立性を調べて、それらを取り出すと

$\displaystyle{(20)\quad \begin{array}{l} B_1,B_2,AB_1 \end{array} }$

を得ます。これを

$\displaystyle{(21)\quad \begin{array}{l} B_1,AB_1,B_2 \end{array} }$

のように並べ替えておきます。 $i=1,2$ に対して、 $A^\nu B_i$ が１次従属となる最小の $\nu$ を可制御性指数と呼びます。まず $i=1$ については、次式より $n_1=2$ となります。

$\displaystyle{(22)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} 7 \\ -1 \\ 3 \end{array}\right] }_{A^2B_1} = \underbrace{7}_{\alpha_{110}} \underbrace{ \left[\begin{array}{c} 1 \\ 0 \\ 0 \end{array}\right] }_{B_1} +\underbrace{(-1)}_{\alpha_{111}} \underbrace{ \left[\begin{array}{c} 0 \\ 1 \\ 0 \end{array}\right] }_{AB_1} +\underbrace{3}_{\alpha_{120}} \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\right] }_{B_2} \end{array} }$

次に $i=2$ については、次式より $n_2=1$ となります。

$\displaystyle{(23)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} 4 \\ -2 \\ 1 \end{array}\right] }_{AB_2} = \underbrace{4}_{\alpha_{210}} \underbrace{ \left[\begin{array}{c} 1 \\ 0 \\ 0 \end{array}\right] }_{B_1} +\underbrace{(-2)}_{\beta_{21}} \underbrace{ \left[\begin{array}{c} 0 \\ 1 \\ 0 \end{array}\right] }_{AB_1} +\underbrace{1}_{\alpha_{220}} \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\right] }_{B_2} \end{array} }$

これらに基づいて、次式を得ます。

$\displaystyle{(24)\quad \begin{array}{l} A \underbrace{ \left[\begin{array}{ccc} B_1 & AB_1 & B_2 \end{array}\right] }_{T_1^{-1}} =\underbrace{ \left[\begin{array}{ccc} B_1 & AB_1 & B_2 \end{array}\right] }_{T_1^{-1}} \underbrace{ \left[\begin{array}{ccc} 0 & \alpha_{110} & \alpha_{210} \\ 1 & \alpha_{111} & \beta_{21}\\ 0 & \alpha_{120} & \alpha_{220} \end{array}\right] }_{A_1}\\ &&B= \underbrace{ \left[\begin{array}{ccc} B_1 & AB_1 & B_2 \end{array}\right] }_{T_1^{-1}} \underbrace{ \left[\begin{array}{cc} 1 & 0 \\ 0 & 0 \\ 0 & 1 \end{array}\right] }_{B_1} \end{array} }$

これから次の第１番目の正準形が定義されます。

$\displaystyle{(25)\quad \begin{array}{l} A_1=T_1AT_1^{-1}= \left[\begin{array}{ccc} 0 & \alpha_{110} & \alpha_{210} \\ 1 & \alpha_{111} & \beta_{21}\\ 0 & \alpha_{120} & \alpha_{220} \end{array}\right] =\left[\begin{array}{ccc} 0 & 7 & 4 \\ 1 & -1 & -2\\ 0 & 3 & 1 \end{array}\right]\\ & B_1=T_1B= \left[\begin{array}{cc} 1 & 0 \\ 0 & 0 \\ 0 & 1 \end{array}\right] \end{array} }$

さて、次式が成り立ちます。

$\displaystyle{(26)\quad \begin{array}{l} &&\underbrace{ \left[\begin{array}{cc|c} 0 & \alpha_{110} & \alpha_{210} \\ 1 & \alpha_{111} & \beta_{21}\\\hline 0 & \alpha_{120} & \alpha_{220} \end{array}\right] }_{A_1} \underbrace{ \left[\begin{array}{cc|c} -\alpha_{111} & 1 & -\beta_{21} \\ 1 & 0 & 0\\\hline 0 & 0 & 1 \end{array}\right] }_{T_2^{-1}}\\ &=\underbrace{ \left[\begin{array}{cc|c} -\alpha_{111} & 1 & -\beta_{21} \\ 1 & 0 & 0\\\hline 0 & 0 & 1 \end{array}\right] }_{T_2^{-1}} \underbrace{ \left[\begin{array}{cc|c} 0 & 1 & 0 \\ \alpha_{110}+\beta_{21}\alpha_{120} & \alpha_{111} & \alpha_{210}+\beta_{21}\alpha_{220}\\\hline \alpha_{120} & 0 & \alpha_{220} \end{array}\right] }_{A_2} \end{array} }$

すなわち

$\displaystyle{(27)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc|c} 0 & 7 & 4 \\ 1 & -1 & -2\\\hline 0 & 3 & 1 \end{array}\right] }_{A_1} \underbrace{ \left[\begin{array}{cc|c} 1 & 1 & 2 \\ 1 & 0 & 0\\\hline 0 & 0 & 1 \end{array}\right] }_{T_2^{-1}} =\underbrace{ \left[\begin{array}{cc|c} 1 & 1 & 2 \\ 1 & 0 & 0\\\hline 0 & 0 & 1 \end{array}\right] }_{T_2^{-1}} \underbrace{ \left[\begin{array}{cc|c} 0 & 1 & 0 \\ 1 & -1 & 2\\\hline 3 & 0 & 1 \end{array}\right] }_{A_2} \end{array} }$

実際、次のように示されます。

$\displaystyle{(28)\quad \begin{array}{l} {\rm LHS}= \left[\begin{array}{ccc} 0 & \alpha_{110} & \alpha_{210} \\ 1 & \alpha_{111} & \beta_{21}\\ 0 & \alpha_{120} & \alpha_{220} \end{array}\right] \left[\begin{array}{ccc} -\alpha_{111} & 1 & -\beta_{21} \\ 1 & 0 & 0\\ 0 & 0 & 1 \end{array}\right]\\ &= \left[\begin{array}{ccc} \alpha_{110} & 0 & \alpha_{210} \\ 0 & 1 & 0 \\ \alpha_{120} & 0 & \alpha_{220} \end{array}\right] \end{array} }$

$\displaystyle{(29)\quad \begin{array}{l} {\rm RHS}=\\ & \left[\begin{array}{ccc} -\alpha_{111} & 1 & -\beta_{21} \\ 1 & 0 & 0\\ 0 & 0 & 1 \end{array}\right] \left[\begin{array}{ccc} 0 & 1 & 0 \\ \alpha_{110}+\beta_{21}\alpha_{120} & \alpha_{111} & \alpha_{210}+\beta_{21}\alpha_{220}\\ \alpha_{120} & 0 & \alpha_{220} \end{array}\right]\\ &= \left[\begin{array}{ccc} \alpha_{110} & 0 & \alpha_{210} \\ 0 & 1 & 0 \\ \alpha_{120} & 0 & \alpha_{220} \end{array}\right] \end{array} }$

上の関係式(??)に基づいて、次の第２番目の正準形が定義されます。

$\displaystyle{(30)\quad \begin{array}{l} &A_2=T_2A_1T_2^{-1}= \left[\begin{array}{ccc} 0 & 1 & 0 \\ 1 & -1 & 2\\ 3 & 0 & 1 \end{array}\right]\\ & B_2=T_2B_1= \left[\begin{array}{cc} 0 & 0 \\ 1 & -2 \\ 0 & 1 \end{array}\right] \end{array} }$

これは次のような表現が可能です。

$\displaystyle{(31)\quad \begin{array}{l} & A_2=A_0+B_0G_0^{-1}F_0\\ & B_2=B_0G_0^{-1} \end{array} }$

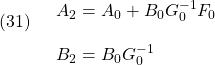
ただし

$\displaystyle{(32)\quad \begin{array}{l} &A_0= \left[\begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & 0\\ 0 & 0 & 0 \end{array}\right],\ B_0= \left[\begin{array}{cc} 0 & 0 \\ 1 & 0 \\ 0 & 1 \end{array}\right]\\ &F_0= \left[\begin{array}{cc|c} \alpha_{110} & \alpha_{111} & \alpha_{210}\\\hline \alpha_{120} & 0 & \alpha_{220} \end{array}\right] = \left[\begin{array}{cc|c} 7 & -1 & 4\\\hline 3 & 0 & 1 \end{array}\right]\\ &&G_0= \left[\begin{array}{cc} 1 & -\beta_{21} \\ 0 & 1 \end{array}\right] = \left[\begin{array}{cc} 1 & 2 \\ 0 & 1 \end{array}\right] \end{array} }$

したがって、 $A_2-B_2F_2$ の特性多項式を

$\displaystyle{(33)\quad \begin{array}{l} \det(\lambda I_3-A_2+B_2F_2)=(\lambda^2+a_1'\lambda+a_2')(\lambda+a_3') \end{array} }$

とする $F_2$ の一つは、次式で与えられます。

$\displaystyle{(34)\quad \begin{array}{l} F_2=F_0+ \left[\begin{array}{ccccc} a_2' & a_1' & 0\\ 0 & 0 & a_3' \end{array}\right] \end{array} }$

実際

$\displaystyle{(35)\quad \begin{array}{l} A_2-B_2F_2= \left[\begin{array}{ccc} 0 & 1 & 0 \\ -a_2' & -a_1' & 0\\ 0 & 0 & -a_3' \end{array}\right] \end{array} }$

[3]　多入力系の場合を考えます。 $B$ の $i$ 番目の列ベクトルを $B_i$ と表すとき

$\displaystyle{(36)\quad \begin{array}{l} B_1,\cdots,B_m,AB_1,\cdots,AB_m,A^2B_1,\cdots,A^2B_m,\cdots \end{array} }$

の順にベクトルの１次独立性を調べて、 $A^\nu B_i$ が１次従属となる最小の $\nu$ として可制御性指数

$\displaystyle{(37)\quad \begin{array}{l} n_1,\ n_2,\ \cdots,\ n_m \end{array} }$

を定めます。得られた１次独立なベクトルを

$\displaystyle{(38)\quad \begin{array}{l} B_1,\cdots,A^{n_1-1}B_1,\cdots,B_m,\cdots,A^{n_m-1}B_m \end{array} }$

のように並べ替えておきます。このとき

$\displaystyle{(39)\quad \begin{array}{l} A^{n_i}B_i=\sum_{j=1}^{m} \left[\begin{array}{ccc} B_j\ \cdots\ A^{n_j-1}B_j \end{array}\right]\alpha_{ij} \end{array} }$

ただし

$\displaystyle{(40)\quad \begin{array}{l} \alpha_{ij}= \left\{\begin{array}{l} \left[\begin{array}{c} \alpha_{ij0} \\ \vdots \\ \alpha_{ij,n_j-1} \end{array}\right]\ (n_j\le n_i)\\ \left[\begin{array}{c} \alpha_{ij0} \\ \vdots \\ \alpha_{ij,n_i-1}\\ \beta_{ij} \\ 0_{n_j-n_i-1\times 1} \\ \end{array}\right]\ (j<i, n_j>n_i)\\ \left[\begin{array}{c} \alpha_{ij0} \\ \vdots \\ \alpha_{ij,n_i-1}\\ 0 \\ 0_{n_j-n_i-1\times 1} \\ \end{array}\right]\ (j>i, n_j>n_i) \end{array}\right. \end{array} }$

が成り立ちます。これから、次式を得ます。

$\displaystyle{(41)\quad \begin{array}{l} A \underbrace{ \left[\begin{array}{c|c|c} B_1\ \cdots\ A^{n_1-1}B_1 & \cdots & B_m\ \cdots\ A^{n_m-1}B_m \end{array}\right] }_{T_1^{-1}}\\ =\underbrace{ \left[\begin{array}{c|c|c} B_1\ \cdots\ A^{n_1-1}B_1 & \cdots & B_m\ \cdots\ A^{n_m-1}B_m \end{array}\right] }_{T_1^{-1}}\\ \times \underbrace{ \left[\begin{array}{c|c|c} \begin{array}{c|c} \begin{array}{c} 0_{1\times n_1-1} \\ I_{n_1-1} \end{array} & \alpha_{11} \end{array} &\cdots & \begin{array}{c|c} 0_{n_1\times n_m-1} & \alpha_{m1} \end{array} \\\hline \vdots & \cdots & \vdots \\\hline \begin{array}{c|c} 0_{n_m\times n_1-1} & \alpha_{1m} \end{array} & \cdots & \begin{array}{c|c} \begin{array}{c} 0_{1\times n_m-1} \\ I_{n_m-1} \end{array} & \alpha_{mm} \end{array} \end{array}\right] }_{A_1}\\ B= \underbrace{ \left[\begin{array}{c|c|c} B_1\ \cdots\ A^{n_1-1}B_1 & \cdots & B_m\ \cdots\ A^{n_m-1}B_m \end{array}\right] }_{T_1^{-1}}\\ \times \underbrace{ \left[\begin{array}{c|c|c} \begin{array}{c} 1 \\ 0_{n_1-1\times1} \end{array} &\cdots & 0_{n_1\times1} \\\hline \vdots & \cdots & \vdots \\\hline 0_{n_m\times1} & \cdots & \begin{array}{c} 1 \\ 0_{n_m-1\times1} \end{array} \end{array}\right] }_{B_1} \end{array} }$

これに基づいて、次の第１番目の正準形が定義されます。

$\displaystyle{(42)\quad \boxed{ \begin{array}{l} A_1=T_1AT_1^{-1}= \left[\begin{array}{c|c|c} \begin{array}{c|c} \begin{array}{c} 0_{1\times n_1-1} \\ I_{n_1-1} \end{array} & \alpha_{11} \end{array} &\cdots & \begin{array}{c|c} 0_{n_1\times n_m-1} & \alpha_{m1} \end{array} \\\hline \vdots & \cdots & \vdots \\\hline \begin{array}{c|c} 0_{n_m\times n_1-1} & \alpha_{1m} \end{array} & \cdots & \begin{array}{c|c} \begin{array}{c} 0_{1\times n_m-1} \\ I_{n_m-1} \end{array} & \alpha_{mm} \end{array} \end{array}\right]\\ B_1=T_1B= \left[\begin{array}{c|c|c} \begin{array}{c} 1 \\ 0_{n_1-1\times1} \end{array} &\cdots & 0_{n_1\times1} \\\hline \vdots & \ddots & \vdots \\\hline 0_{n_m\times1} & \cdots & \begin{array}{c} 1 \\ 0_{n_m-1\times1} \end{array} \end{array}\right] \end{array}} }$

さて、次式が成り立ちます。(この証明はまだ完成していません)

$\displaystyle{(43)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c|c|c} \begin{array}{c|c} \begin{array}{c} 0_{1\times n_1-1} \\ I_{n_1-1} \end{array} & \alpha_{11} \end{array} &\cdots & \begin{array}{c|c} 0_{n_1\times n_m-1} & \alpha_{m1} \end{array} \\\hline \vdots & \cdots & \vdots \\\hline \begin{array}{c|c} 0_{n_m\times n_1-1} & \alpha_{1m} \end{array} & \cdots & \begin{array}{c|c} \begin{array}{c} 0_{1\times n_m-1} \\ I_{n_m-1} \end{array} & \alpha_{mm} \end{array} \end{array}\right] }_{A_1}\\ \times \underbrace{ \left[\begin{array}{ccc} L_{11} & \cdots & L_{m1} \\ \vdots & \cdots & \vdots \\ L_{1m} & \cdots & L_{mm} \end{array}\right] }_{T_2^{-1}} =\underbrace{ \left[\begin{array}{ccc} L_{11} & \cdots & L_{m1} \\ \vdots & \cdots & \vdots \\ L_{1m} & \cdots & L_{mm} \end{array}\right] }_{T_2^{-1}} \underbrace{ (A_0+B_0G_0^{-1}F_0) }_{A_2} \end{array} }$

ただし

$\displaystyle{(44)\quad \begin{array}{l} L_{ii}=-\left[\begin{array}{ccc} S_{n_i}\alpha_{ii} & \cdots & S_{n_i}^{n_i}\alpha_{ii} \end{array}\right]+J_{n_1}\\ L_{ij}=-\left[\begin{array}{ccc} S_{n_j}\alpha_{ij} & \cdots & S_{n_j}^{n_i}\alpha_{ij} \end{array}\right]\\ S_\nu= \left[\begin{array}{cc} 0_{\nu-1\times 1} & I_{\nu-1}\\ 0 & 0_{1\times\nu-1} \end{array}\right] \\ J_\nu= \left[\begin{array}{ccc} 0 & \cdots & 1 \\ \vdots & \cdot & \vdots \\ 1 & \cdots & 0 \end{array}\right] \end{array} }$

および

$\displaystyle{(45)\quad \begin{array}{l} A_0= \left[\begin{array}{c|c|c} S_{n_1} & \cdots & 0_{n_1\times n_m} \\\hline \vdots & \ddots & \vdots \\\hline 0_{n_m\times n_1} & \cdots & S_{n_m} \end{array}\right]\\ B_0= \left[\begin{array}{c|c|c} \begin{array}{c} 0_{n_1-1\times 1} \\ 1 \end{array} & \cdots & 0_{n_1\times1} \\\hline \vdots & \ddots & \vdots \\\hline 0_{n_m\times1} & \cdots & \begin{array}{c} 0_{n_m-1\times 1} \\ 1 \end{array} \end{array}\right]\\ F_0= \left[\begin{array}{ccc|c|ccc} \bar\alpha_{110} & \cdots & \bar\alpha_{11,n_1-1} & \cdots & \bar\alpha_{m10} & \cdots & \bar\alpha_{m1,n_m-1}\\ \vdots & \cdots & \vdots & \cdots & \vdots & \cdots & \vdots \\ \bar\alpha_{1m0} & \cdots & \bar\alpha_{1m,n_1-1} & \cdots & \bar\alpha_{mm0} & \cdots & \bar\alpha_{mm,n_m-1}\\ \end{array}\right]\\ \bar\alpha_{ijk}= \left\{\begin{array}{ll} \alpha_{ijk} & (k\verb|<| n_j)\\ 0 & (k\ge n_j)\end{array}\right.\\ G_0=\left[\begin{array}{cccl} 1&\bar\beta_{21}&\cdots&\bar\beta_{m1}\\ 0&1&\ddots&\vdots\\ \vdots&\ddots&\ddots&\bar\beta_{m,m-1}\\ 0&0&\cdots&1\end{array}\right]\\ \bar\beta_{ij}=\left\{\begin{array}{ll} -\beta_{ij} &(n_j\ge n_i)\\ 0 &(n_j\verb|<|n_i) \end{array}\right. \end{array} }$

次の第２番目の正準形が定義されます。

$\displaystyle{(46)\quad \boxed{\begin{array}{l} A_2=A_0+B_0G_0^{-1}F_0\\ B_2=B_0G_0^{-1} \end{array}} }$