2次系のステップ応答…Homework
[0] 次の![]() 入力
入力![]() 出力
出力![]() 次系の状態空間表現を考えます。
次系の状態空間表現を考えます。
![]()
いま行列![]() の第
の第![]() 列を
列を![]() 、行列
、行列![]() の第
の第![]() 列を
列を![]() で表すとき、第
で表すとき、第![]() 番目の入力
番目の入力![]() から第
から第![]() 番目の出力
番目の出力![]() までの時間応答は
までの時間応答は
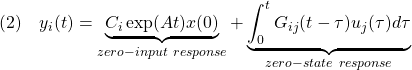
のように表されます。ここで、![]() は(1)のインパルス応答行列の
は(1)のインパルス応答行列の![]() 要素で、次のように与えられます。
要素で、次のように与えられます。
![]()
このときステップ入力
![]()
に対する零状態応答はステップ応答と呼ばれ、インパルス応答を積分して
![]()
のように計算されます。
[1] さて、次のようにパラメタライズされた漸近安定な1入力1出力2次系の状態空間表現を考えます。
![Rendered by QuickLaTeX.com \displaystyle{(6a)\quad \underbrace{ \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} 0 & 1\\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{cc} 0 \\ K\omega_n^2 \end{array}\right] }_{B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-163123fac605973ff5bb7e352fe8a4e4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6b)\quad y(t)= \underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c9800fcc5420d0c26c37f1aa628b4db9_l3.png)
以下では、簡単のため![]() とした2次系(7)に対するインパル応答を(6)から求めます。そのために、行列
とした2次系(7)に対するインパル応答を(6)から求めます。そのために、行列![]() の固有値
の固有値![]() を計算すると、
を計算すると、![]() 、
、![]() 、
、![]() に応じて、それぞれ次に示すようになります。
に応じて、それぞれ次に示すようになります。
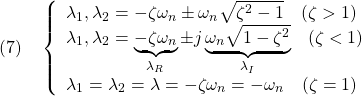
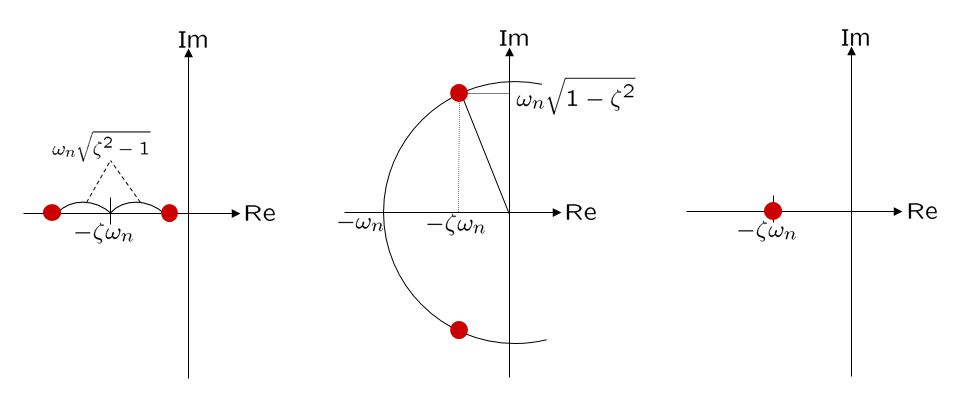 図1
図1 ![]() の固有値分布
の固有値分布
[3] 2次系のステップ応答(1)
![]() のとき、
のとき、![]() とおくと、インパルス応答とステップ応答はそれぞれ次式で与えられます。
とおくと、インパルス応答とステップ応答はそれぞれ次式で与えられます。
![]()
![]()
実際、インパルス応答を積分して、ステップ応答は次のように計算されます。
![Rendered by QuickLaTeX.com (9)\quad \begin{array}{l} \displaystyle{S(t)=\int_0^tG(\tau)d\tau=\int_0^t\frac{\lambda_1 \lambda_2}{\lambda_2-\lambda_1}(e^{\lambda_2\tau}-e^{\lambda_1\tau})d\tau}\\ \displaystyle{= \frac{\lambda_1 \lambda_2}{\lambda_2-\lambda_1}\left[\frac{e^{\lambda_2\tau}}{\lambda_2}-\frac{e^{\lambda_1\tau}}{\lambda_1}\right]_0^t}\\ \displaystyle{=\frac{\lambda_1 \lambda_2}{\lambda_2-\lambda_1}(\frac{e^{\lambda_2t}}{\lambda_2}-\frac{e^{\lambda_1t}}{\lambda_1})-\frac{\lambda_1 \lambda_2}{\lambda_2-\lambda_1}(\frac{1}{\lambda_2}-\frac{1}{\lambda_1})}\\ \displaystyle{=1+\frac{1}{\lambda_2-\lambda_1}(\lambda_1e^{\lambda_2t}-\lambda_2e^{\lambda_1t})} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-71159c7ee47771d4db9ea63f64ac8347_l3.png)
[4] 2次系のステップ応答(2)
![]() のとき、
のとき、![]() とおくと、インパルス応答とステップ応答はそれぞれそれぞれ次式で与えられます。
とおくと、インパルス応答とステップ応答はそれぞれそれぞれ次式で与えられます。
![]()
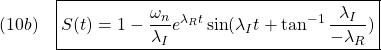
実際、インパルス応答を積分して、公式
![]()
を用いて、ステップ応答は次のように計算されます。
![Rendered by QuickLaTeX.com (12)\quad \begin{array}{l} \displaystyle{S(t)=\int_0^tG(\tau)d\tau=\int_0^t\frac{\omega_n^2}{\lambda_I}e^{\lambda_R\tau}\sin\lambda_I \tau d\tau}\\ \displaystyle{=\frac{\omega_n^2}{\lambda_I}\left[ \frac{e^{\lambda_R\tau}}{\lambda_R^2+\lambda_I^2}(\lambda_R\sin\lambda_I\tau-\lambda_I\cos\lambda_I\tau)\right]_0^t}\\ \displaystyle{=\frac{\omega_n^2}{\lambda_I}\frac{1}{\omega_n^2} (e^{\lambda_Rt}(\lambda_R\sin\lambda_It-\lambda_I\cos\lambda_It)+\lambda_I)}\\ \displaystyle{=1-\frac{\omega_n}{\lambda_I}e^{\lambda_Rt} (\sin\lambda_It\times\frac{-\lambda_R}{\omega_n}+\cos\lambda_It\times\frac{\lambda_I}{\omega_n})}\\ \displaystyle{=1-\frac{\omega_n}{\lambda_I}e^{\lambda_Rt} (\sin\lambda_It\cos\phi+\cos\lambda_It\sin\phi)}\\ \displaystyle{=1-\frac{\omega_n}{\lambda_I}e^{\lambda_Rt}\sin(\lambda_It+\phi) \quad(\phi=\tan^{-1}\frac{\lambda_I}{-\lambda_R})} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-70211d9c75bdadc0383d2b9c1b25fa64_l3.png)
[5] 2次系のステップ応答(3)
![]() のとき、
のとき、![]() とおくと、インパルス応答とステップ応答はそれぞれそれぞれ次式で与えられます。
とおくと、インパルス応答とステップ応答はそれぞれそれぞれ次式で与えられます。
![]()
![]()
実際、インパルス応答を積分して、ステップ応答は次のように計算されます。
![Rendered by QuickLaTeX.com (14)\quad \begin{array}{l} \displaystyle{S(t)=\int_0^tG(\tau)d\tau=\int_0^t\lambda^2\tau e^{\lambda\tau}d\tau}\\ \displaystyle{=\lambda^2\left[\tau \frac{1}{\lambda}e^{\lambda\tau}\right]_0^t -\lambda^2\int_0^t \frac{1}{\lambda}e^{\lambda\tau}d\tau}\\ \displaystyle{=\lambda te^{\lambda t}-\lambda\left[\frac{1}{\lambda}e^{\lambda\tau}\right]_0^t}\\ \displaystyle{=1+(\lambda t-1)e^{\lambda t}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f57dc1b1984646aeeeaafbb17bfcee60_l3.png)
2次振動系の同定…Homework
[6] 2次系(6)において、![]() 、
、![]() 、
、![]() の場合、ステップ応答のシミュレーション例を示します。
の場合、ステップ応答のシミュレーション例を示します。
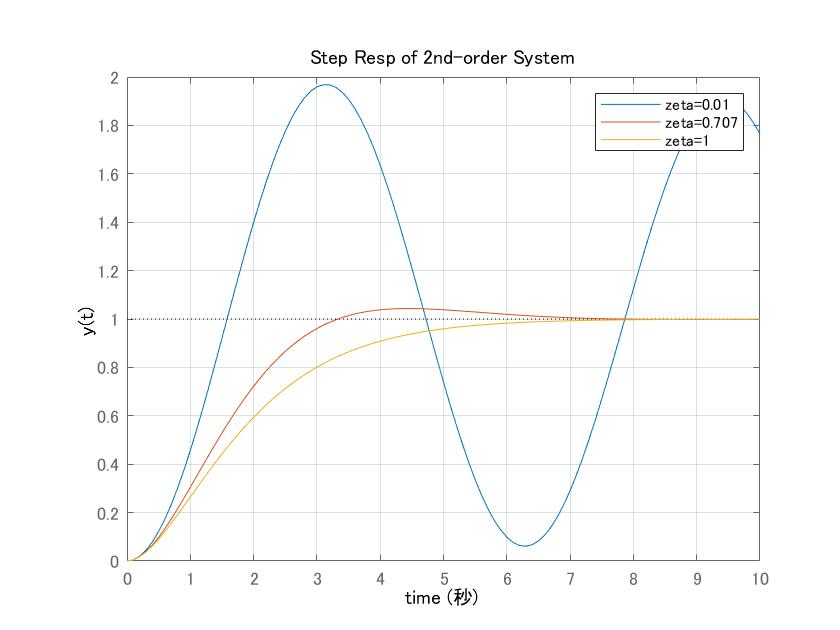 図2 2次系のステップ応答の比較
図2 2次系のステップ応答の比較
![]() の場合の(7)で表される2次系を2次振動系と呼びます。そのステップ応答
の場合の(7)で表される2次系を2次振動系と呼びます。そのステップ応答
![]()
の第1オーバーシュートについて、次が成り立ちます。
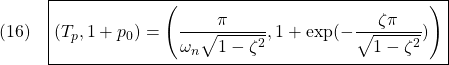
実際、![]() を計算すると
を計算すると
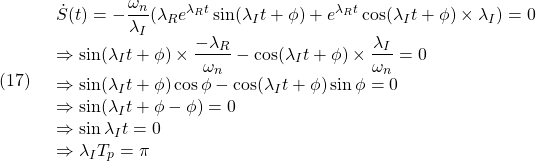
となって、次式を得ます。
![]()
この時刻![]() における
における![]() の値は
の値は
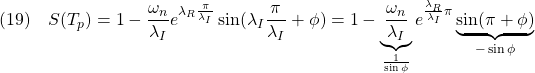
となって、次式を得ます。
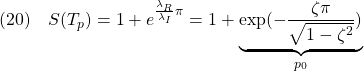
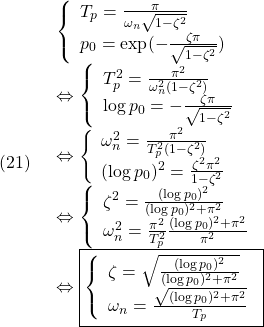
●したがって、次のように、![]() から
から![]() を得ることができます。
を得ることができます。
演習A23…Flipped Classroom
図2のステップ応答#1を描き、第1オーバーシュートの頂点の座標![]() をマウスをクリックして取得し、減衰係数と固有角周波数
をマウスをクリックして取得し、減衰係数と固有角周波数![]() を求めるプログラムを作成せよ。
を求めるプログラムを作成せよ。
| MATLAB |
|
| SCILAB |
|