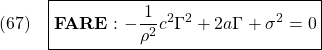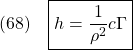1次系のLQ制御…Homework
[1] ある平衡状態周りの挙動が状態方程式
![]()
で表される制御対象に対して、状態フィードバック(state feedback)
![]()
を考えます。ここで、定数![]() はゲインと呼ばれ、
はゲインと呼ばれ、![]() を満たすものを選びます。(2)を(1)に代入して、次式を得ます。
を満たすものを選びます。(2)を(1)に代入して、次式を得ます。
![]()
これは制御対象とコントローラ(状態フィードバック)が閉路を構成することから(図1参照)、閉ループ系(closed-loop system)と呼ばれます。ここで、物理的に興味深いのは、制御対象が漸近安定でなくても(![]() )、状態フィードバックを行って閉ループ系を漸近安定(
)、状態フィードバックを行って閉ループ系を漸近安定(![]() )にできることです。そのようなゲイン
)にできることです。そのようなゲイン![]() を決定する問題を状態フィードバックによる安定化問題と言います。
を決定する問題を状態フィードバックによる安定化問題と言います。
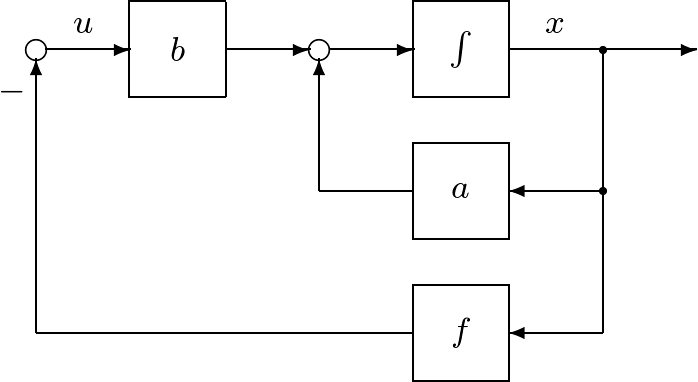 図1 状態フィードバックによる閉ループ系
図1 状態フィードバックによる閉ループ系
[2] 1次系(1)に対する安定化状態フィードバック(2)による閉ループ系に対して、評価関数
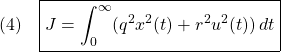
を最小化するように![]() を決めるLQ制御問題を考えます。
を決めるLQ制御問題を考えます。
●閉ループ系における状態の振舞いは次式で与えられます。
![]()
したがって、評価関数(4)の第1項は、次式のように計算されます。
![Rendered by QuickLaTeX.com (6)\quad \begin{array}{lll} \displaystyle{J_x=\int_0^\infty q^2x^2(t)\,dt}\\ \displaystyle{=\int_0^\infty q^2e^{2(a-bf)t}x^2(0)\,dt}\\ \displaystyle{=q^2x^2(0)\left[\frac{1}{2(a-bf)}e^{2(a-bf)t}\right]_0^\infty}\\ \displaystyle{=\frac{q^2x^2(0)}{2(a-bf)}\left[\underbrace{e^{2(a-bf)\infty}}_{0}-\underbrace{e^{2(a-bf)0}}_{1}\right]}\\ \displaystyle{=-\frac{q^2}{2(a-bf)}x^2(0)>0\quad (a-bf<0)} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ccbd56eae6c871c4d509a66bb0b1d13c_l3.png)
これから![]() を大きくすれば、
を大きくすれば、![]() はいくらでも小さくできることが分かります。
はいくらでも小さくできることが分かります。
●閉ループ系における入力の振舞い![]() は次式で与えられます。
は次式で与えられます。
![]()
したがって、評価関数(4)の第2項は、次式のように計算されます。
![Rendered by QuickLaTeX.com (8)\quad \begin{array}{lll} \displaystyle{J_u=\int_0^\infty r^2u^2(t)\,dt}\\ \displaystyle{=\int_0^\infty r^2f^2e^{2(a-bf)t}x^2(0)\,dt}\\ \displaystyle{=r^2f^2x^2(0)\left[\frac{1}{2(a-bf)}e^{2(a-bf)t}\right]_0^\infty}\\ \displaystyle{=-\frac{r^2f^2}{2(a-bf)}x^2(0)>0\quad (a-bf<0)} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9f5dcb6b69a84056f569669f6625e961_l3.png)
![]() が下に凸で、
が下に凸で、 ![]() において最小値を取ることは、次式から分かります。
において最小値を取ることは、次式から分かります。
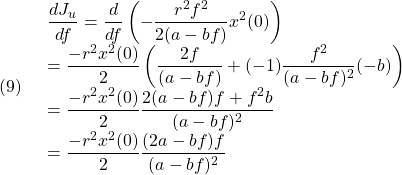
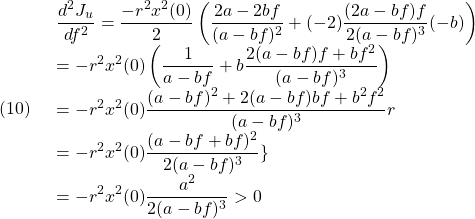
いま、![]() として、
として、![]() と
と![]() の場合について、
の場合について、![]() 、
、![]() 、
、![]() の外形を描くと、次図のようになります。ここで、
の外形を描くと、次図のようになります。ここで、![]() には○で示す最小値が生まれていることに注意してください。
には○で示す最小値が生まれていることに注意してください。
●それでは![]() の最小値を与える
の最小値を与える![]() を求めてみます。評価関数は
を求めてみます。評価関数は
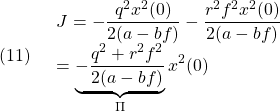
のように書けますので、![]() の最小化は、次の
の最小化は、次の![]() の最小化と等価です。
の最小化と等価です。
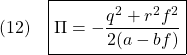
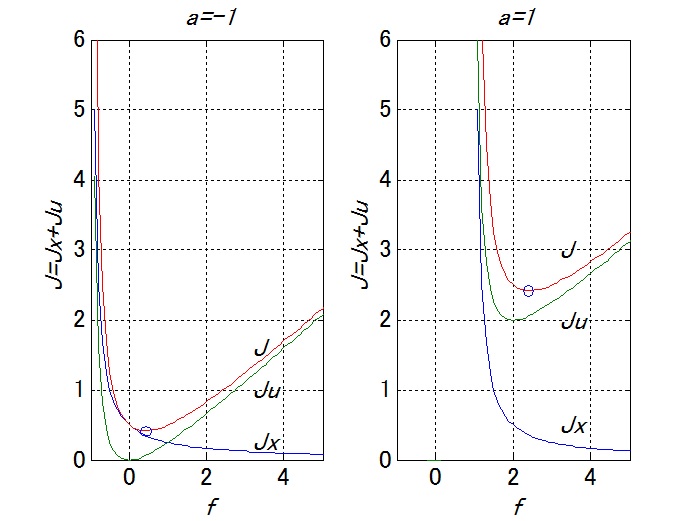 図2 評価関数の概形
図2 評価関数の概形
●この極値を求めるために![]() で微分すると
で微分すると
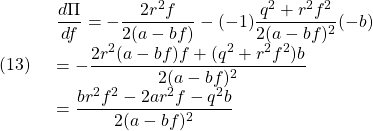
これより
![]()
ここで、![]() は
は ![]() を満足させるものでなければならないので
を満足させるものでなければならないので
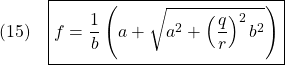
となります。そしてこれが一意に定まることは、以下のように![]() が下に凸でであることから分かります。
が下に凸でであることから分かります。
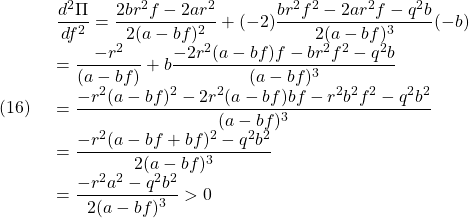
[2] LQ制御問題の解は求まったので、今度は評価関数(4)の重み係数![]() と
と![]() の与え方について考えます。まず被積分項
の与え方について考えます。まず被積分項![]() は物理量の2乗和になっていますので、予め代表時間と代表長さによる無次元化を行っておく必要があります。たとえば、状態変数と入力変数がとりうる範囲を想定して
は物理量の2乗和になっていますので、予め代表時間と代表長さによる無次元化を行っておく必要があります。たとえば、状態変数と入力変数がとりうる範囲を想定して
![]()
とすると、重み係数は物理単位の無次元化の役割を果たすことになります。次に(15)による閉ループ系を考えます。
![]()
ここで、![]() の場合を考えると
の場合を考えると
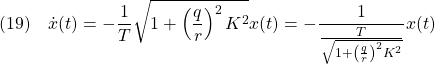
となって、新しい時定数は元の時定数![]() より小さくなることが分かります。これを決めるパラメータは重み係数の比
より小さくなることが分かります。これを決めるパラメータは重み係数の比![]() で、これが大きいほど時定数
で、これが大きいほど時定数![]() は小さくなります。
は小さくなります。
●パラメータ![]() を導入して重み係数を次のように設定します。
を導入して重み係数を次のように設定します。
![]()
ここで、![]() は固定されますので、設計パラメータは
は固定されますので、設計パラメータは![]() のみになります。
のみになります。
![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() として、設計パラメータを
として、設計パラメータを![]() と変えてみると、次の応答を得ます。
と変えてみると、次の応答を得ます。
 図3 重み係数の比
図3 重み係数の比![]() による応答の変化
による応答の変化
演習A03-1…Flipped Classroom
![]() 図2のグラフを描け。またパラメータ
図2のグラフを描け。またパラメータ![]() の値による状態と入力の振る舞いを観察し、トレードオフの関係について述べよ。
の値による状態と入力の振る舞いを観察し、トレードオフの関係について述べよ。
| MATLAB |
|
| SCILAB |
|
![]() ハミルトン行列と呼ばれる
ハミルトン行列と呼ばれる
![]()
の安定な固有値
![]()
に対応する固有ベクトルは
![Rendered by QuickLaTeX.com \displaystyle{(23)\quad \left[\begin{array}{cc} v_1 \\ v_2 \end{array}\right] =\left[\begin{array}{cc} 1 \\ \frac{-a-\sqrt{a^2+r^{-2}b^2q^2}}{-r^{-2}b^2} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-818b80fae6a9d75606e700bc7229ad17_l3.png)
となることを確かめ、次式を計算せよ。
![]()
状態オブザーバ…Homework
[3] 状態フィードバックを使うには状態変数の変化をセンサで捉えてフィードバックする必要があるのですが、状態方程式が分かっているのですから、これを計算機内で解いてやれば良いのではないでしょうか?
いま制御対象(1次系)の状態空間表現を
![]()
とします。これを計算機で解きますが、その状態と出力を区別して
![]()
で表します。(26)から(25)の第1式どうしを辺々引くと
![]()
を得ます。ここで![]() でない限り
でない限り
![]()
とはなりません。そこで、図4に示すような工夫が行われました。
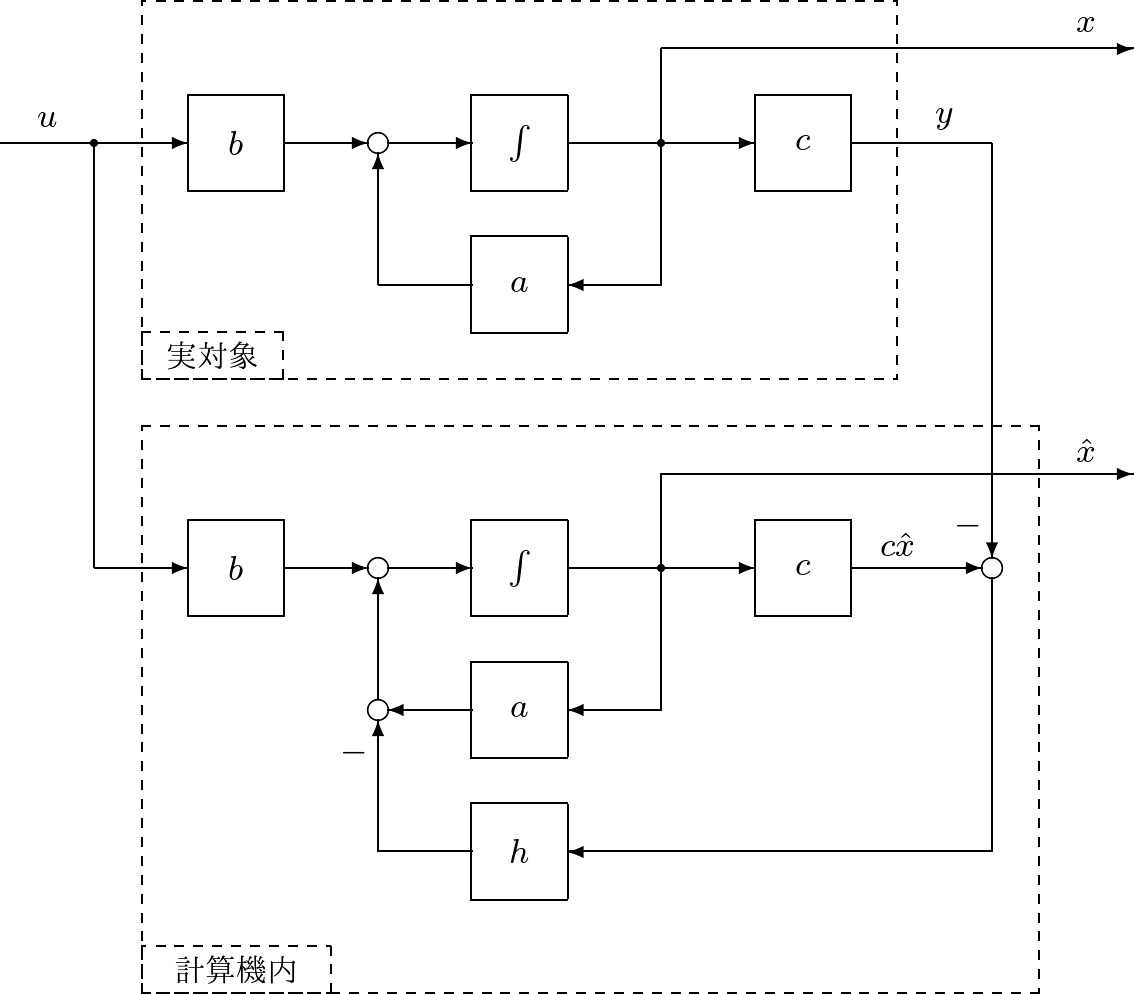 図4 状態オブザーバの考え方
図4 状態オブザーバの考え方
● いま(2)に次のような補正項を加えます。
![]()
すなわち
![]()
ここで、![]() は適当な定数です。(30)から(26)の第1式どうしを辺々引くと
は適当な定数です。(30)から(26)の第1式どうしを辺々引くと
![]()
を得ます。ここで![]() であるとすると
であるとすると
![]()
が成り立ちます。すなわち状態オブザーバ(30)の状態![]() は、制御対象の状態
は、制御対象の状態![]() を漸近的に推定することができます。このとき
を漸近的に推定することができます。このとき![]() を満たす(30)を状態オブザーバ、
を満たす(30)を状態オブザーバ、![]() をオブザーバゲインと呼びます。
をオブザーバゲインと呼びます。
● 1次系
![]()
に対して、状態オブザーバ
![]()
によって推定された状態![]() を用いる状態フィードバック
を用いる状態フィードバック
![]()
による閉ループ系の状態方程式は、次式となります。
![Rendered by QuickLaTeX.com \displaystyle{(36)\quad \left[\begin{array}{cc} \dot{x}(t)\\ \dot{\hat{x}}(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} a& -bf\\ hc& a-hc-bf \end{array}\right] }_{A_F} \left[\begin{array}{cc} x(t)\\ \hat{x}(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bd0bda91887ef926493669aa7866308d_l3.png)
これから閉ループ系の安定性を判定したいのですが、このままでは見当がつきません。そこで、状態の推定誤差を![]() とおくと、状態変数を変更した閉ループ系の状態方程式として、次式を得ます。
とおくと、状態変数を変更した閉ループ系の状態方程式として、次式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(37)\quad \boxed{ \left[\begin{array}{cc} \dot{x}(t)\\ \dot{e}(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} a-bf & -bf\\ 0 & a-hc \end{array}\right] }_{A_F'} \left[\begin{array}{cc} x(t)\\ e(t) \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-36b6d2d539455492f72a79c84bbd9dfe_l3.png)
実際、状態の推定誤差の定義から、
![]()
に注意すると、状態フィードバック(35)は
![]()
これによる閉ループ系は、![]() に代入して
に代入して
![]()
となります。これが(37)の第1式に他なりません。また、第2式は(31)そのもの、すなわち次式となります。
![]()
閉ループ系の状態方程式は(40)と(41)に分離されており、![]() と
と![]() は共に負となるように
は共に負となるように![]() と
と![]() を独立に設計してもよいことが分かります。この事実は分離定理と呼ばれています。
を独立に設計してもよいことが分かります。この事実は分離定理と呼ばれています。
なお状態フィードバックを状態オブザーバの出力を用いて実施するコントローラ
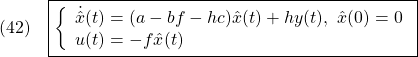
は、オブザーバベースコントローラと呼ばれています。
演習A03-2…Flipped Classroom
![]() 1次系
1次系![]() に対する状態フィードバック
に対する状態フィードバック![]() と,状態オブザーバ
と,状態オブザーバ![]() (
(![]() )を考える。状態オブザーバによって推定された状態を用いる状態フィードバック
)を考える。状態オブザーバによって推定された状態を用いる状態フィードバック![]() による閉ループ系の状態方程式を求めよ。
による閉ループ系の状態方程式を求めよ。
![]() 閉ループ系の
閉ループ系の![]() 行列の固有値が
行列の固有値が
![]() ,
,![]() (
(![]() )となるように,
)となるように,![]() と
と![]() を定めよ。
を定めよ。
![]() と
と![]() に,
に,![]() と
と![]() をどう対応させたか,およびその理由を述べよ。
をどう対応させたか,およびその理由を述べよ。
1次系のLQG制御…Homework
[5] 1次系(33)に対して、オブザーバベースコントローラ(42)による閉ループ系に対して、評価関数
![]()
を最小化するように、状態フィードバックゲイン![]() と状態オブザーバゲイン
と状態オブザーバゲイン![]() を決定するLQG制御問題を考えます。
を決定するLQG制御問題を考えます。
●評価関数は次のように計算できます。
状態方程式
![Rendered by QuickLaTeX.com \displaystyle{(44)\quad \underbrace{ \left[\begin{array}{cc} \dot{x}(t)\\ \dot{e}(t) \end{array}\right] }_{\dot{x}_{CL}(t)} = \underbrace{ \left[\begin{array}{cc} a-bf & -bf\\ 0 & a-hc \end{array}\right] }_{A_{CL}} \underbrace{ \left[\begin{array}{cc} x(t) \\ e(t) \end{array}\right] }_{x_{CL}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-18643919f74aadae99e3d8cd8e1b5bdb_l3.png)
と出力方程式
![Rendered by QuickLaTeX.com \displaystyle{(45)\quad \underbrace{ \left[\begin{array}{cc} qx(t)\\ ru(t) \end{array}\right] }_{y_{CL}(t)} = \underbrace{ \left[\begin{array}{cc} q & 0 \\ -rf & -rf \end{array}\right] }_{C_{CL}} \underbrace{ \left[\begin{array}{cc} x(t) \\ e(t) \end{array}\right] }_{x_{CL}(t)} \label{eq7.2.5}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-684ce689df1ece17dac2a773360c137d_l3.png)
で表される閉ループ系の応答は
|
<このパートは最初は読み飛ばして結構です> このとき
|
ここで、初期値
![]()
をどう選ぶかですが、図4に示す閉ループ系を考えます。すなわち、(33)の代わりに、
![]()
を考えます。ここで、新たに加えられた入力![]() と
と![]() はそれぞれシステムノイズと観測ノイズとよばれ、定常正規確率過程として扱うのが普通です。特に、
はそれぞれシステムノイズと観測ノイズとよばれ、定常正規確率過程として扱うのが普通です。特に、![]() と
と![]() は分散を表しています。ここでは確率的な議論を避けるため、
は分散を表しています。ここでは確率的な議論を避けるため、![]() と
と![]() は確定的なインパルス入力であると仮定します。
は確定的なインパルス入力であると仮定します。
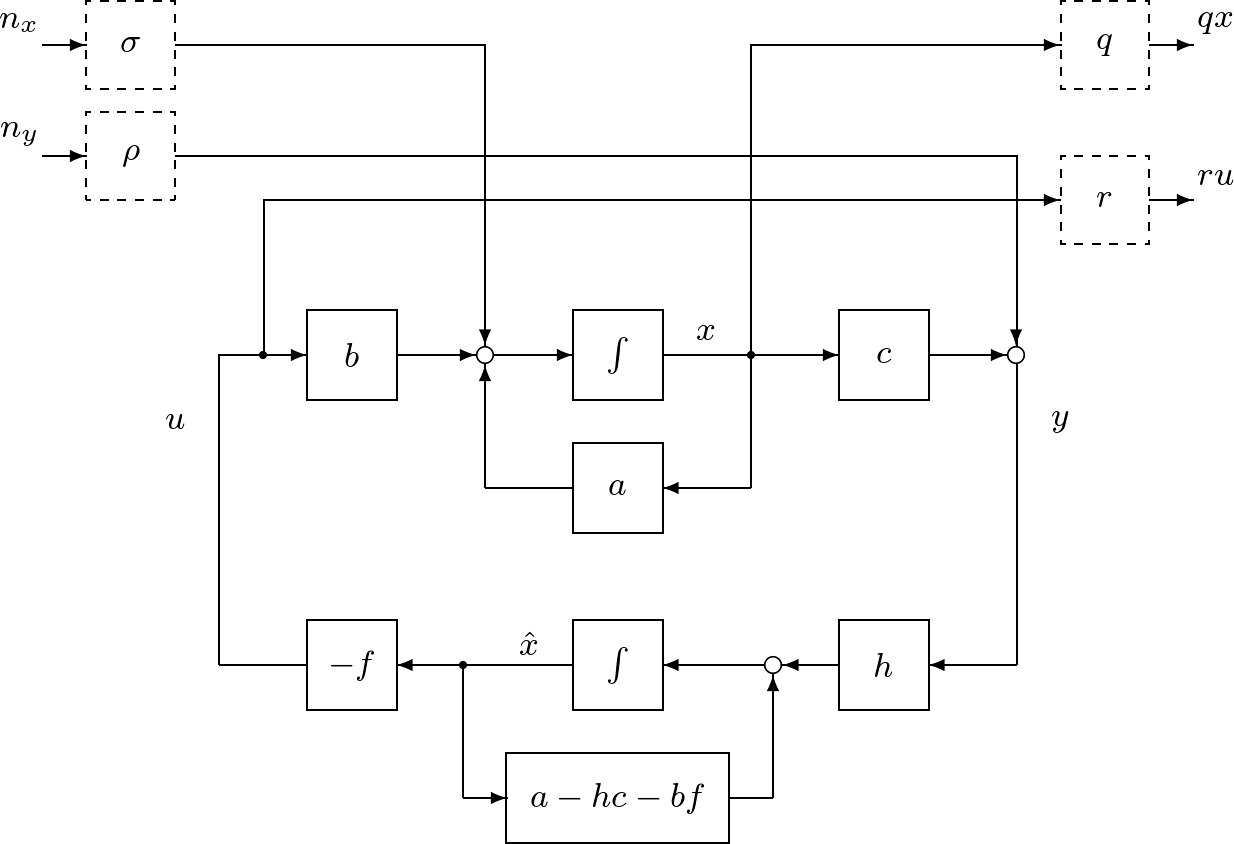
図5 オブザーバベース・コントローラによる閉ループ系の評価
このとき、閉ループ系の状態方程式は、次式となります。
![Rendered by QuickLaTeX.com \displaystyle{(50)\quad &&\left[\begin{array}{cc} \dot{x}(t)\\ \dot{e}(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} a-bf & -bf \\ 0 & a-hc \end{array}\right] }_{A_{CL}} \left[\begin{array}{cc} x(t)\\ e(t) \end{array}\right]\nonumber\\ &&+ \underbrace{ \left[\begin{array}{cc} \sigma & 0\\ -\sigma & h\rho \end{array}\right] }_{B_{CL}} \left[\begin{array}{cc} n_x(t)\\ n_y(t) \end{array}\right] \label{eq7.2.11}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3dae61b87dbc3a1048d873c29e860e77_l3.png)
出力方程式(45)の場合のインパルス応答は、インパルス入力を![]() に与える場合と
に与える場合と![]() に与える場合の2通り
に与える場合の2通り
<このパートは最初は読み飛ばして結構です>![Rendered by QuickLaTeX.com \displaystyle{(51)\quad y^{(1)}_{CL}(t) = C_{CL}\exp(A_{CL}t) \underbrace{ \left[\begin{array}{cc} \sigma \\ -\sigma \end{array}\right] }_{x_{CL}(0)=B^{(1)}_{CL}} \label{eq7.2.12}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6d85ddaaacfba1399baf629b17e45713_l3.png)
|
があるので、評価関数を改めて次式のように両者の2乗和とします。
![]()
これは、![]() とおくと
とおくと
![]()
と計算できます。ここで、![]() を直接計算することは容易ではないのですが、
を直接計算することは容易ではないのですが、
|
<このパートは最初は読み飛ばして結構です>
|
すなわち
![]()
![]()
![]()
の解であることに等しいという結果を用います。
(56)より![]() を求めれば,評価関数は
を求めれば,評価関数は
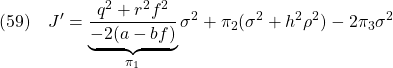
となります。ここで,第1項は,(11)で,![]() としたものであることに注意します。いま,
としたものであることに注意します。いま,![]() かつ
かつ![]() という場合を考えてみると,(50)の第2行目より
という場合を考えてみると,(50)の第2行目より
![]()
だから,(35)は状態フィードバック![]() に相当します。この場合の議論はすでに行っており,
に相当します。この場合の議論はすでに行っており,![]() は存在しないので,評価関数(59)は第1項だけとなり,これを最小化する
は存在しないので,評価関数(59)は第1項だけとなり,これを最小化する![]() は,リッカチ方程式
は,リッカチ方程式
![]()
の解![]() を用いて次のように与えられます。
を用いて次のように与えられます。
![]()
そうすると,評価関数(59)の第2項と第3項は,状態オブザーバを用いるために生じると考えられます。このように,理想的な状態フィードバックに比べて評価関数の値が増えることを評価関数の劣化と呼びます。
つぎに,仮定![]() ,
,![]() ,
,![]() のもとでは,(57)より
のもとでは,(57)より![]() を得ます。このとき,式(58)は
を得ます。このとき,式(58)は
![]()
となり,これから![]() が求まります。したがって,評価関数(59)は
が求まります。したがって,評価関数(59)は
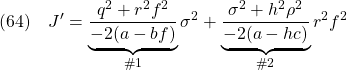
と書けます。評価関数の劣化分を最小化するためには,#2を![]() について最小化すればよいことになります。幸いなことに,#2は#1と同形であるので,これを最小化する
について最小化すればよいことになります。幸いなことに,#2は#1と同形であるので,これを最小化する![]() の決定法は
の決定法は![]() と同様に行ないます。
と同様に行ないます。
●以上の議論をまとめると、次のようになります。
|
アルゴリズム <1次系のLQG制御>
入力パラメータ ステップ1: 状態フィードバックゲイン
を解いて,
ステップ2: オブザーバゲイン
を解いて,
ステップ3: オブザーバベース コントローラの構成
ただし
|
●![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() として、状態フィードバックだけとオブザーバベース コントローラを用いた場合とを比較してみると、次の応答を得ます。
として、状態フィードバックだけとオブザーバベース コントローラを用いた場合とを比較してみると、次の応答を得ます。
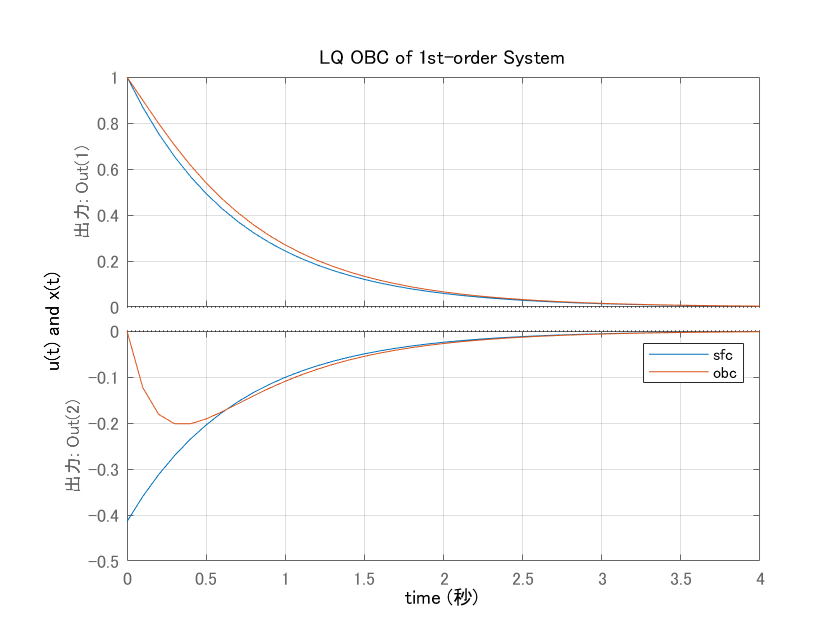 図6 状態フィードバックとオブザーバベース コントローラを用いた場合の応答の変化
図6 状態フィードバックとオブザーバベース コントローラを用いた場合の応答の変化
演習A03-3…Flipped Classroom
![]() 図6のグラフを描け。
図6のグラフを描け。
| MATLAB |
|
| SCILAB |
|
![]() 上のシミュレーションにおいて、
上のシミュレーションにおいて、![]() となっていることを確かめよ。
となっていることを確かめよ。
Note A03 ラグランジュの未定定数法
1入力1出力1次系に対する最適制御(LQ制御)を考えましたが、一般の多入力多出力高次系の場合も同様な議論ができて、大変有用な制御手段として知られています。その説明はあとで行ないますが、そこではラグランジュの未定定数法によるアプローチが採用されます。
(11)の評価関数![]() を最小化する問題を、
を最小化する問題を、![]() をラグランジュの未定定数として
をラグランジュの未定定数として
![]()
を最小化する問題として考え直してみます。ここで、制約条件は、リャプノフ方程式と呼ばれる
![]()
ですが、![]() は
は![]() を意味することに注意します。そこで、必要条件として次を得ます。
を意味することに注意します。そこで、必要条件として次を得ます。
![]()
![]()
![]()
ここで、第2式から得られる![]() を第3式に代入して
を第3式に代入して
![]()
すなわち、リッカチ方程式と呼ばれる![]() の2次方程式
の2次方程式
![]()
を得ます。これから![]() を
を
![]()
を求めて、![]() は
は
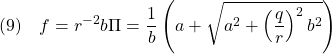
のように得られます。十分性の議論はここでは省きます。
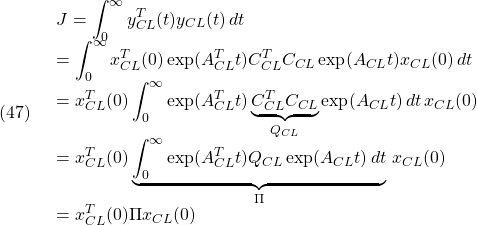
![Rendered by QuickLaTeX.com \displaystyle{(52)\quad y^{(2)}_{CL}(t) = C_{CL}\exp(A_{CL}t) \underbrace{ \left[\begin{array}{cc} 0 \\ h\rho \end{array}\right] }_{x_{CL}(0)=B^{(2)}_{CL}} \label{eq7.2.13}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d2090f3554280d4f6ace06c772a5f0c6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(55)\quad \begin{array}{lll} && \underbrace{ \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] }_{\Pi} \underbrace{ \left[\begin{array}{cc} a-bf & -bf \\ 0 & a-hc \end{array}\right] }_{A_{CL}}\nonumber\\ &&+ \underbrace{ \left[\begin{array}{cc} a-bf & 0 \\ -bf & a-hc \end{array}\right] }_{A_{CL}^T} \underbrace{ \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] }_{\Pi}\nonumber\\ &&+ \underbrace{ \left[\begin{array}{cc} q^2+r^2f^2 & r^2f^2 \\ r^2f^2 & r^2f^2 \end{array}\right] }_{C_{CL}^TC_{CL}>0} = \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right] \end{array} \label{eq7.2.16}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-79305e587239433bbc038b894b5d433c_l3.png)