「未分類」カテゴリーアーカイブ
問・演習問題の解答(1章)
問1.1 十分大きな 問1.2 問1.3 答は図1.12。 問1.4 座標変換
【1】 回路方程式はつぎのように整理できる。
ブロック線図は図3.4参照。 【2】
【3】 状態方程式??を考えると,平衡状態では
式??からこれを辺々引いて,つぎの状態方程式を得る。
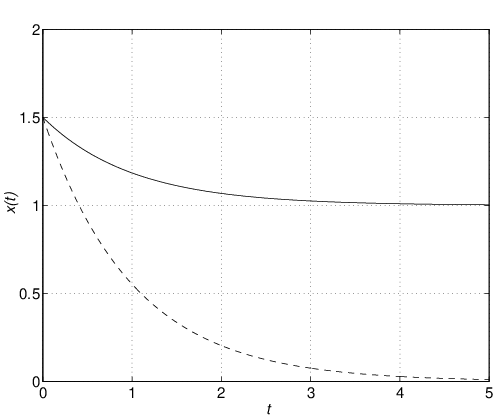
【4】 シミュレーション結果はつぎのとおり。
|
8. 伝達関数から状態方程式を導く
|
線形系を知るということは,インパルス応答を知るということにほかならない。というのは,どのような入力が与えられても,インパルス応答とのたたみこみ積分を行って出力(零状態応答)が得られるからである。インパルス応答をラプラス変換したものを「伝達関数」と呼ぶ。ステップ応答の微分がインパルス応答であり,周波数応答の逆フーリエ変換がやはりインパルス応答であるから,実際には,「システム同定」実験を通してステップ応答や周波数応答を得て(伝達関数を陰に陽に求めて),さまざまな制御方式を設計することがよく行われている。
一方,これまで私たちは,物理法則に基づいて状態方程式と出力方程式からなる状態空間表現を得ていたが,もし同定実験を通して得られた伝達関数から状態空間表現を求めることができれば,これまで学んださまざまな特性解析・コントローラ設計の方法を適用できるであろう。インパルス応答や伝達関数は線形系の入出力関係を表すので「外部記述」と呼ばれ,これに対応する状態空間表現は「内部記述」と呼ばれる。そして,外部記述から内部記述を求めることを「実現」という。 本章では,状態空間表現の構造のより深い理解のためもあって,この実現問題を扱う。実は,与えられた外部記述に対応する状態空間表現は無数に存在する。これは状態空間の次数と座標軸の取り方に自由度が存在するためである。特に,最小次数の状態空間表現を求めることを「最小実現」という。興味深いのは,最小次数が可制御かつ可観測の性質により特徴付けられることである。また,座標軸の適切な取り方の一つに,特に信号処理分野で有用性が認められている「平衡実現」と呼ばれるものがある。 |
7. 非線形の運動方程式から始める
|
これまで扱ってきた制御対象は,その運動方程式が線形の微分方程式で表される「線形系」としていた。ところが実際には,例えば,ロボットアームの運動方程式に見られるように,非線形の微分方程式で表される「非線形系」が多い。このとき,これまで学んできた線形系に対する制御理論(LQ制御やLQI制御)はどのように役立つのだろうか。
まず,運動方程式(高階の非線形微分方程式)から「非線形状態方程式」を1階の連立非線形微分方程式として求めておく。つぎに,物理的な釣り合いの状態,すなわち「平衡状態」を考える。その平衡状態付近での運動を,「線形化」された状態方程式で表し,これに対して例えばLQI制御を適用する。 このアプローチは1入力1出力系ばかりでなく多入力多出力系に対しても適用できて,これまで数多くの制御問題の解決が図られてきた。その実績こそが,前章までに述べてきた線形システム制御論の有用性を示唆し,これを学ぶことの強い動機付けを与えている。 そこで,本章では,運動方程式が非線形の微分方程式で表される対象の制御問題として,水タンクの水位制御問題を考え,LQI制御を適用しながら線形システム制御論に基づくアプローチを説明する。皆さんは,計算機を用いて,LQIコントローラの数値計算と閉ループ系の時間応答シミュレーションに挑戦してほしい。そして,できれば適当な制御実験を試みてほしい。自分で考えたアルゴリズムで物をうまく動かすことができたときは,きっと小躍りしたくなるであろう。 |
6. 定値外乱を抑制する
| これまで,安定性の定義,安定化の可能性とその方策を学んできた。その結果,私たちは,閉ループ系の零入力応答を適切に安定化する,すなわち,ある初期状態から出発して速やかに零状態(平衡状態)にもっていくことはできる。この零入力応答は,適当な強さのインパルス入力に対する零状態応答に等しいことを思い出してほしい。
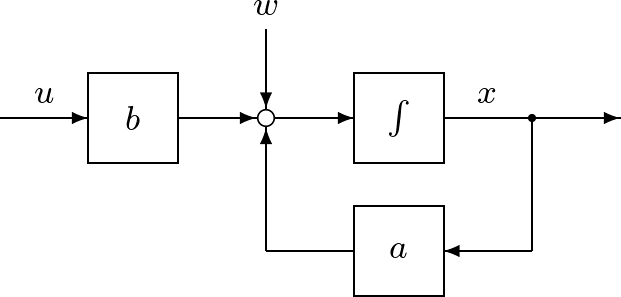
例えば,一定速度で回転しているモータを考え,これに瞬間的な負荷がかかって,その速度が乱されたとする。このときは,状態フィードバックによってもとの速度に復帰させることができる。しかし,モータで何か対象物を回転させるときは,モータ軸への持続的な負荷が生じ,極端な場合はモータは回転することさえできないであろう。同様に,飛行機,船舶,車などのビークルに強い向い風が吹けば定速を維持することは困難となるであろう。 また,モータやビークルでは,速度の設定値を変えることが制御の大切な役割なのに,そのための手段はまったく学んでいない。 したがって,これまでの知識だけでは多くの現実問題を解くことはできない。実際の問題では,必ずといっていいほど,さまざまな「定値外乱」の影響を受ける状況のもとで,「設定値」の保持や,ときには変更を要求されるからである。このような問題を解決するためには,これまでの制御方式に加えて,まず「積分動作」の導入による構造的な改良が必要となる。本章では,定値外乱の影響の除去や,設定値の変更に対応できるように,積分動作を入れて安定化を行う方策について学ぶ。その安定化にLQ制御を適用するとき,その制御方式を簡潔に表すために「LQI制御」と呼ぶ。 |
6.1 1次系における定値外乱の影響を抑制する
6.1.1 定値外乱の影響
| 1章で述べた直流モータの状態方程式(1.11)すなわち
を思い出そう。これは,二つの入力変数 以下では,この状況を一般化した次式で表される1次系を考える。
ここで,
いま,1次系(2)に対して,状態フィードバック
を行うと,閉ループ系
を得る。ここで,
となる。第2項は
と計算できるので,
すなわち,定値外乱が加わると
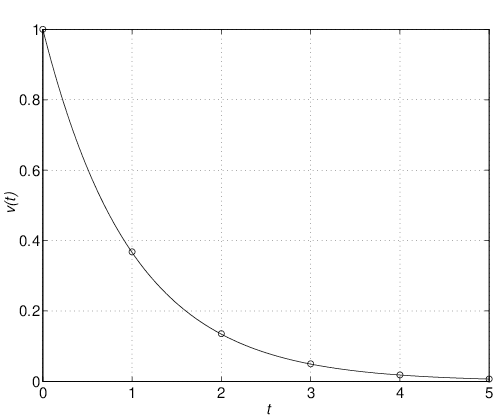
とはならない。このことをシミュレーション例で確認しよう。 シミュレーション 6.1
このような定値外乱の影響を取り除くために,式(3)の代わりに
のような方策を用いる。このときの閉ループ系
の時間応答は
となる。これより,外乱を打ち消すように
と選べば,式(8)を達成できる。しかしながら, |
図6.2の下に次の問を設定していましたが,紙幅の関係で省略しました。
図6.2で,![]() であることを確かめなさい。
であることを確かめなさい。
6.1.2 積分動作を加える
| この方法の基礎となるアイデアは
を達成できれば そこで,式(13)を満足する
を達成することができないか検討しよう。 まず,式(2)と,式(13)の
を合わせて
を構成する。式(16)に
を代入すると,閉ループ系は
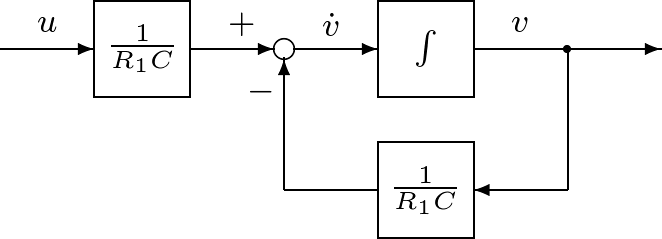
となる。そのブロック線図を図6.3に示す。
さて,
となる。ここで,
と計算できるから
と表される。したがって
を得る。ここで
となり,外乱の影響が抑制されていることと,式(14)が成り立つことが確認できる。また,式(17)からつぎが成り立つ。
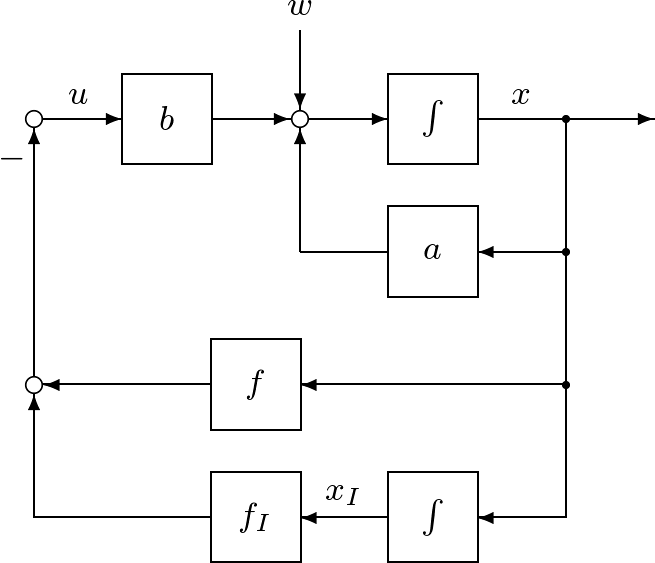
シミュレーション6.2
|
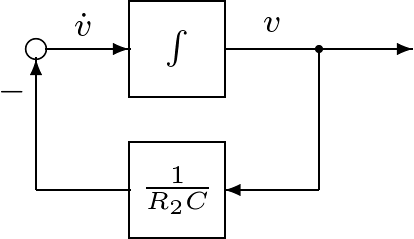
図6.4の下に次の問を設定していましたが,紙幅の関係で省略しました。
図6.4で,![]() ,
,![]() であることを確かめなさい。
であることを確かめなさい。
また,(19),(20),(21)におい![]() であることに注意してください。
であることに注意してください。
6.1.3 設定値を変更する
| 前節では,定値外乱の加わる1次系
に対して,制御目的
を達成する方法を学んだ。ここでは,任意の定数
を達成する問題を考える。この
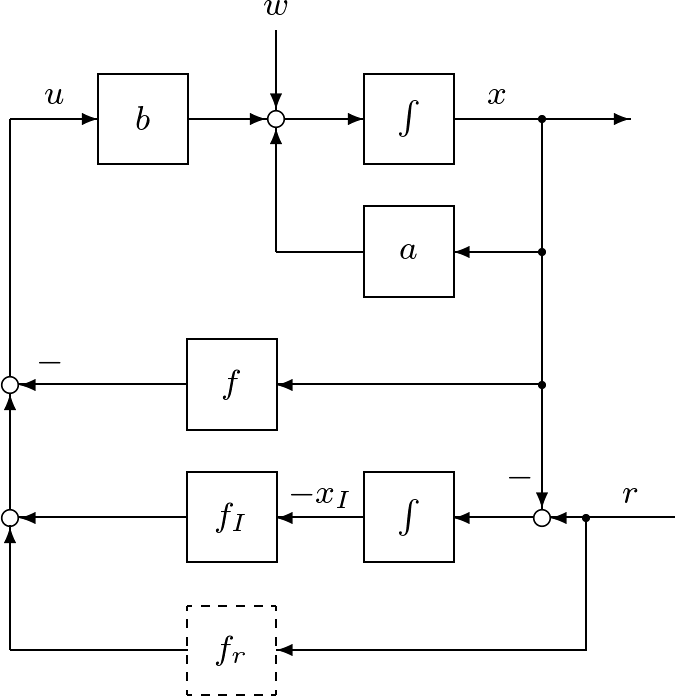
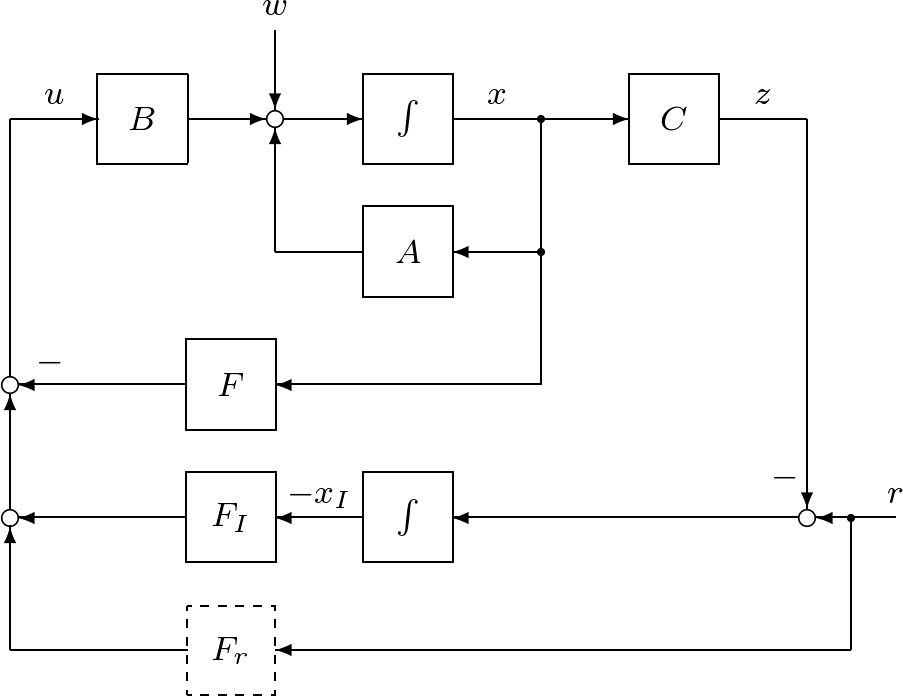
この問題の解決のためには,外乱を抑制するための図6.4を,図6.5に示すように変更すればよい。実際,式(27)を
のような積分動作を導入すればよいことに気づくであろう。 式(25)と式(26)を合わせて
を構成する。いま,式(29)に
を代入すると
となる。
を得る。この第1行は,
を得る。ここで,設定値
また,つぎが成り立つ。
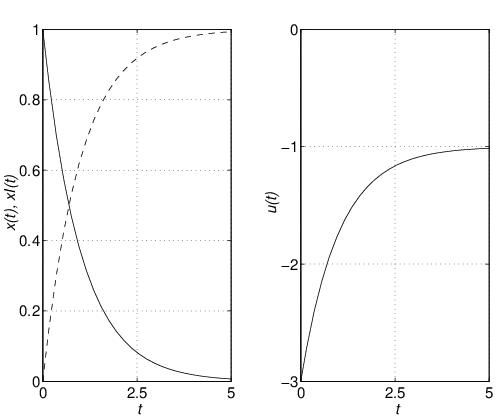
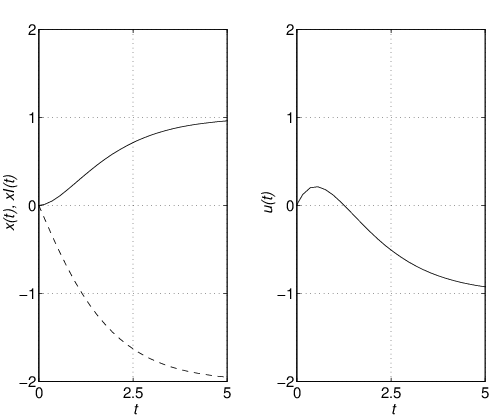
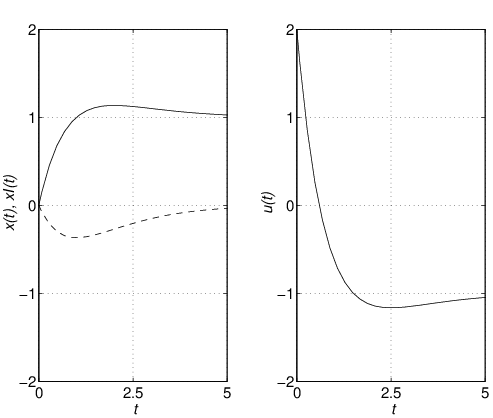
それでは,フィードフォワード項による速応性改善の効果をシミュレーションによって確かめよう。 シミュレーション6.3
問6.1 |
6.2 積分型コントローラ
6.2.1 積分動作を加えた状態フィードバック
| 次式で表される可制御かつ可観測で,
ここで,状態方程式には,操作入力
のように選び(
を達成したい。ここで,定数ベクトル
の関係を満足しているはずである。したがって,どのような
が成り立つように選ぶものとする。
さて,制御目的(39)を達成するために,図6.8に示すような,つぎの積分動作を加えた状態フィードバックを考える。
ここで,第2項は積分動作を表している。このように
を得る。式(36)と式(43)を合わせて
を得る。式(44)に,式(42)すなわち
を代入すると,閉ループ系は,つぎのように表される。
いま,
よって,
を用いて
ここで,
のように計算される。ところで,式(46)から
を得る。この第1ブロック行は,式(40)より
となって,式(40)の第2ブロック行から制御目的(39)が成り立つ。また,式(50)の第2ブロック行から
を得る。ここで,設定値
のように表され,ここで,
|
6.2.2 積分動作を加えたオブザーバベース\,コントローラ
| 式(42)の代わりに,実際には,状態オブザーバ
の出力を用いて
を実施することになる。ここでの積分動作を加えたオブザーバベース\,コントローラは,式(56)を式(55)に代入した
と,式(43)を合わせて,つぎのように表される。
これによる閉ループ系は,式(56)を式(36)に代入した
と,式(43),(57)を合わせて
のように表される。そのブロック線図を図6.9に示す。
いま,閉ループ系(61)に,座標変換
を行えば
となり,閉ループ系の固有値は,積分動作を加えた状態フィードバックだけの閉ループ系の固有値と状態オブザーバの固有値からなる。 ここで,
すなわち
を得る。したがって,定値外乱が存在するときは状態オブザーバに関して定常偏差が残るにもかかわらず,制御目的(39)が成り立つことがわかる。また,フィードフォーワードゲイン |
6.3 LQI設計
| これまで,閉ループ系(18),(31),(46),(63)において, 制御目的(39)が達成されたとき成り立つ式(40)より
を得る( 偏差系E1: この両辺を微分すれば,状態変数の中の定数ベクトルを除くことができて 偏差系E2: を得る。さらに,式(36)と(38)をまとめた
から式(40)を引いて,つぎの関係式が成り立つ。
これに基づいて,偏差系E2に座標変換を行えば 偏差系E3: を得る。ここで,つぎの関係式を用いた。
問6.2 問6.3 例えば,偏差系E1に対して,状態フィードバック
を用いて,閉ループ系を安定化すれば, 以下に,偏差系E3をLQ制御により安定化して,積分動作を加えたオブザーバベース\,コントローラを構成する手順を示す。 アルゴリズム6.1 <LQI設計> 入力パラメータ1 出力パラメータ ステップ1 被制御変数の決定
ステップ2 偏差系の安定化 偏差系
を,状態フィードバック
によるLQ制御で安定化する。その際,評価関数としては
を用いる。ただし, さらに,
ステップ3 オブザーバゲイン 例えば,アルゴリズム5.2のステップ2を用いる。
を解いて,
ステップ4 LQIコントローラの構成
ただし
この積分動作を加えたオブザーバベース\,コントローラを簡潔にLQIコントローラ}(LQI controller),これによる制御方式をLQI制御(LQ control with integral action)と呼ぶ。 問6.4 |
|
前章までに,状態フィードバックと状態オブザーバを組み合わせた安定化コントローラ(オブザーバベース\,コントローラ)を,どのような条件のもとで構成できるかについて検討し,それが可制御性と可観測性(可安定性と可検出性)であることを述べた。そこでつぎに,状態フィードバックと状態オブザーバの構成を合理的に行うことを考えたい。
まず,状態フィードバックについては,代表的な方法として最小2乗規範に基づく方法がある。これは,状態フィードバックによる閉ループ系における時間応答の2乗面積が最小となるように,状態フィードバックゲインを定めるものである。ここで,状態変数の時間的振る舞いの2乗面積ばかりでなく,どのような入力を用いて閉ループ系を構成したかを評価するために,入力変数の時間的振る舞いの2乗面積についても同時に考えることが肝要である。こうして得られる制御方式を,状態フィードバックによる「LQ制御」と呼ぶ。この状態フィードバックゲインは,「リッカチ方程式」と呼ばれる行列に関する2次方程式を解いて求めることができる。 つぎに,状態オブザーバについてであるが,オブザーバベース\,コントローラによる閉ループ系における時間応答の2乗面積の和を最小化する立場から考える。この値は,理想的な状態フィードバックだけの場合と比べて,状態オブザーバを用いるので増加(劣化)する。そこで,この増分が小さくなるようにオブザーバゲインを定めることが行われる。 本章で述べる制御方式は「最適制御」と呼ばれるものの一つで,歴史的には「LQG理論」として確率システムの制御の立場から研究されてきた。しかし,ここでは確定的な議論にとどめて,主要な結果を説明した。 |
4. センサが足りないが大丈夫か
|
前章で,状態フィードバックによって安定化可能である条件(可安定性)や閉ループ系の固有値を任意に設定できる条件(可制御性)を学んだ。ただし,すでに指摘しておいたように,状態フィードバックという制御手段は,すべての状態変数にセンサを付けること( \par それでは,状態オブザーバは,制御対象の状態空間表現が与えられるとき,いつでも構成可能なのであろうか。答えはノーである。状態オブザーバが構成可能な条件は「可検出性」として知られている。可検出性は,前章で学んだ可安定性と密接な関係(双対関係)にある。これについて学ぶのが本章の一つの目標である。可安定性を強めた概念として可制御性があったように,可検出性を強めた概念として「可観測性」があり,これについても本章で学ぶ。最後に,2~4章の重要な結論として,制御対象の安定化可能条件が可安定性と可検出性であり,その手段がオブザーバベース\,コントローラであることを述べる。 |
3. いつ安定化できるのか
|
前章で,状態方程式から安定性を調べる方法を学んだ。すなわち,対象が安定であるとは さて,状態フィードバックによって安定化可能である条件は「可安定性」と呼ばれるが,これを直接明らかにするのは容易ではない。そこで,状態フィードバックによって |
特異値分解(singular-value decomposition)
——————————————————————————————————————–
定理 ![]() をサイズ
をサイズ![]() の行列(
の行列(![]() )とする。このとき,サイズ
)とする。このとき,サイズ![]() の直交行列
の直交行列![]() とサイズ
とサイズ![]() の直交行列
の直交行列![]() が存在して
が存在して
(1) ![]()
が成り立つ。ここで,サイズ![]() の行列
の行列![]() は,次を満たす(
は,次を満たす(![]() は,
は,![]() がサイズ
がサイズ![]() の行列であることを示す(
の行列であることを示す(![]() は行数と列数の区切)。)。
は行数と列数の区切)。)。
(2) ![]()
(3) ![]()
を満足するものである。
証明 ![]() だから,仮定
だから,仮定![]() より,
より,![]() は
は![]() 個の正固有値と
個の正固有値と![]() 個の零固有値をもち,互いに直交する固有ベクトルをもつ。そこで,
個の零固有値をもち,互いに直交する固有ベクトルをもつ。そこで,![]() の固有値の正の平方根を,大きい順に,
の固有値の正の平方根を,大きい順に,![]() のように表し,対応する固有ベクトル
のように表し,対応する固有ベクトル![]() を
を![]() を満足するようにとることができる。いま,
を満足するようにとることができる。いま,![]() を式3のように,また
を式3のように,また
(4) ![]()
とおくと,![]() は直交行列となり,つぎが成り立つ。
は直交行列となり,つぎが成り立つ。
(5) ![]()
(6) ![]()
式6の第2式の左から,![]() をかけて
をかけて
(7) ![]()
また,![]() とおくと,式6の第1式から
とおくと,式6の第1式から![]() を得る。そこで,
を得る。そこで,![]() を
を![]() が直交行列となるように選ぶと
が直交行列となるように選ぶと
(8) ![]()
が成り立つ。これより,式1を得る。
——————————————————————————————————————–
——————————————————————————————————————–
例題 行列![]() の特異値分解は
の特異値分解は
(9) ![Rendered by QuickLaTeX.com \begin{equation*} A= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right] }_{U} \underbrace{ \left[\begin{array}{ccc} \sqrt{2} & 0 & 0 \\ 0 & 1 & 0 \end{array}\right] }_{\Sigma} \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0 \\ \frac{1}{\sqrt{2}} & 0 & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \end{array}\right]^T }_{V^T} \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-094ad853e40d20871e2bb59827a7a28d_l3.png)
のように与えられることを確かめなさい。
解答 ![]() のサイズは
のサイズは![]() であるが,
であるが,![]() のサイズは
のサイズは![]() であるので,
であるので,![]() を計算すると
を計算すると![]() となる(サイズ
となる(サイズ![]() の行列
の行列![]() の特異値を手計算で求めるには,
の特異値を手計算で求めるには,![]() と
と![]() のが同じ非零固有値をもつことから,サイズの小さいほうの固有値計算を行えばよい。)。これから,
のが同じ非零固有値をもつことから,サイズの小さいほうの固有値計算を行えばよい。)。これから,![]() の固有値は
の固有値は![]() で,その正の平方根
で,その正の平方根![]() が特異値であるが,定理??の
が特異値であるが,定理??の![]() の対角成分の特異値は大きい順に並べる約束であるので
の対角成分の特異値は大きい順に並べる約束であるので
(10) ![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{cc} 1 & 0 \\ 0 & 2 \end{array}\right] }_{AA^T} \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right] }_{U} = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right] }_{U} \underbrace{ \left[\begin{array}{cc} 2 & 0 \\ 0 & 1 \end{array}\right] }_{\Sigma_1^2} \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1c6751fd19e4519cddf20df4ebf93762_l3.png)
のように,![]() と
と![]() が決まる。つぎに,
が決まる。つぎに,![]() については,視察によって
については,視察によって
(11) ![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 1 & 1 \end{array}\right] }_{A^TA} \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0 \\ x & 0 & -y \\ y & 0 & x \end{array}\right] }_{V} = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0 \\ x & 0 & -y \\ y & 0 & x \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{ccc} 2 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{array}\right] }_{{\rm diag}\{\Sigma_1^2,0\}} \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9396a30d4e002b6668c2989cc5a0caf5_l3.png)
としてよい。ここで![]() と
と![]() が直交しており,
が直交しており,![]() の制約がある。式(11)から
の制約がある。式(11)から![]() が出て,
が出て,![]() と定まる。
と定まる。
——————————————————————————————————————–
それでは,階段化アルゴリズムについて述べる。
——————————————————————————————————————–
アルゴリズム<階段化アルゴリズム(staircase algorithm)>
入力パラメータ ![]()
出力パラメータ ![]()
ステップ1 初期化
![]() とおく。
とおく。
ステップ2 ![]() の階数決定
の階数決定
![]() を
を![]() に更新し,
に更新し,![]() に対して,つぎの特異値分解を行い,
に対して,つぎの特異値分解を行い,![]() の階数
の階数![]() と
と![]() を求める。
を求める。
(12) ![]()
(13) ![Rendered by QuickLaTeX.com \begin{equation*} \Sigma^{(j)}= \left[\begin{array}{cc} \Sigma_1^{(j)} & 0 \\ 0 & 0 \end{array}\right] \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d67d8188ec3c7b3a7eb6718aa908076b_l3.png)
もし![]() または
または![]() ならば,
ならば,![]() と設定して終了する。そうでないときは,ステップ3へ行く。
と設定して終了する。そうでないときは,ステップ3へ行く。
ステップ3 座標変換
![]() を,
を,![]() を用いて
を用いて
(14) ![]()
と設定し,![]() と
と![]() を,次式から求める。
を,次式から求める。
(15) ![]()
ステップ4 ![]() の切り出し
の切り出し
![]() を
を![]() に更新し,
に更新し,![]() に対してつぎの分割を行い,
に対してつぎの分割を行い,![]() を得て,ステップ2へ戻る。
を得て,ステップ2へ戻る。
(16) ![]()
——————————————————————————————————————–
——————————————————————————————————————–
例題
階段化アルゴリズムを用いて,つぎの可安定性を調べなさい。
(17) ![Rendered by QuickLaTeX.com \begin{equation*} A= \left[\begin{array}{ccc} 0 & 0 & 0 \\ 0 & -1 & 1 \\ 0 & 0 & 0 \end{array}\right] ,\ B= \left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \\ 0 & 1 \end{array}\right] \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b92241244023641047fc6798268d28eb_l3.png)
解答 階段化アルゴリズムの各ステップは,つぎのように計算される。
ステップ1:![]() とおく。
とおく。
ステップ2:![]() とし,
とし,![]() に対する特異値分解
に対する特異値分解
(18) ![Rendered by QuickLaTeX.com \begin{equation*} B^{(1)}= \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 1 \\ \frac{1}{\sqrt{2}} & 0 & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \end{array}\right] }_{U^{(1)}} \underbrace{ \left[\begin{array}{cc} \sqrt{2} & 0 \\ 0 & 1 \\ 0 & 0 \end{array}\right] }_{\Sigma^{(1)}} \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right]^T }_{V^{(1)T}} \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a067f8aaad77ff4216766cffc9192713_l3.png)
から,![]() の階数
の階数![]() と
と![]() が求まる。
が求まる。
ステップ3:![]() かつ
かつ![]() なので,ステップ4へ行く。
なので,ステップ4へ行く。
ステップ4:![]() とし,
とし,![]() を求めると
を求めると
(19) ![Rendered by QuickLaTeX.com \begin{equation*} A^{(2)}= \left[\begin{array}{cc|c} 0 & 0 & 1 \\ 0 & 0 & 0 \\ \hline 0 & 0 & -1 \end{array}\right] \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d83528baa9a88d1f937bdd46679d77ba_l3.png)
となり,![]() とする。
とする。
ステップ5:![]() とする。
とする。![]() に対する分割から,
に対する分割から,![]() を得る。
を得る。
ステップ2′:![]() とする。
とする。![]() は零行列なので,その階数は
は零行列なので,その階数は![]() である。
である。
ステップ3′:![]() なので,
なので,![]() のように設定する。
のように設定する。
以上から,式(24)は,つぎのように得られた。
(20) ![Rendered by QuickLaTeX.com \begin{equation*} \left[\begin{array}{cc} T^TB & T^TAT \end{array}\right]= \left[\begin{array}{ccc} B_1 & A_1 & X \\ 0 & B_2 & A_2 \end{array}\right]= \left[\begin{array}{cc|cc|c} 0 & \sqrt{2} & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 \\ \hline 0 & 0 & 0 & 0 & -1 \end{array}\right] \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a81d3b6a6d9c8a5d2db3d43e85f23312_l3.png)
ここで,![]() は零行列で,
は零行列で,![]() より,条件S0が成り立つ。よって,
より,条件S0が成り立つ。よって,![]() は可安定である。
は可安定である。
——————————————————————————————————————–
まず,可安定性と可制御性は座標変換により不変であることを示す。
——————————————————————————————————————–
定理 ![]() が可安定対[可制御対]ならば,
が可安定対[可制御対]ならば,![]() も可安定対[可制御対]である。
も可安定対[可制御対]である。
証明 ![]() 次系
次系![]() に対する
に対する![]() による安定化可能性は,座標変換後の
による安定化可能性は,座標変換後の![]() に対する
に対する![]() による安定化可能性と等価である。実際
による安定化可能性と等価である。実際
(21) ![]()
が成り立ち,閉ループ系の固有値は,座標変換によって不変だからである。
可制御性については,シルベスターの公式
![]() (
(![]() は
は![]() の列数)
の列数)
を用いて
(22) ![]()
が成り立つことから,定理の主張を得る。
——————————————————————————————————————–
この定理に基づいて,可安定性や可制御性の判別をしやすいように座標変換行列![]() を選ぶことを考える。すなわち,
を選ぶことを考える。すなわち,![]() 次系
次系![]() に対して,つぎを満足するように座標変換できるかどうかを調べる。
に対して,つぎを満足するように座標変換できるかどうかを調べる。
(23) ![Rendered by QuickLaTeX.com \begin{equation*} \left[\begin{array}{c} \dot{x}_1'(t) \\ \dot{x}_2'(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A_{\#} & X \\ 0 & A_k \end{array}\right] }_{TAT^{-1}} \left[\begin{array}{c} x_1'(t) \\ x_2'(t) \end{array}\right] + \underbrace{ \left[\begin{array}{c} B_{\#} \\ 0 \end{array}\right] }_{TB} u(t) \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0a5ef4ada18aa82e6fd7b2b111ee0cd0_l3.png)
ただし,![]() は可制御対とする。このブロック線図を描いてみればわかるように,状態
は可制御対とする。このブロック線図を描いてみればわかるように,状態![]() は入力
は入力![]() の影響を受けることはない。したがって,可制御性は成立しないこと,そして
の影響を受けることはない。したがって,可制御性は成立しないこと,そして![]() が安定行列かどうかが可安定性と関係していることは想像がつくであろう。以下では,この判定法が導かれること示す。
が安定行列かどうかが可安定性と関係していることは想像がつくであろう。以下では,この判定法が導かれること示す。
「式(23)のように座標変換できれば,![]() が安定行列のとき可安定性が成り立ち,そうでないときは可安定性は成り立たない。また,式(23)のように座標変換できなければ,可制御性が成り立っている。」
が安定行列のとき可安定性が成り立ち,そうでないときは可安定性は成り立たない。また,式(23)のように座標変換できなければ,可制御性が成り立っている。」
つぎの結果は,階段化アルゴリズムを用いて得られる。
——————————————————————————————————————–
定理
サイズ![]() の行列
の行列![]() とサイズ
とサイズ![]() の行列
の行列![]() に対して,つぎのように変換する直交行列
に対して,つぎのように変換する直交行列![]() が存在する。
が存在する。
(24) ![Rendered by QuickLaTeX.com \begin{equation*} \left[\begin{array}{cc} T^TB & T^TAT \end{array}\right]= \left[\begin{array}{c|cccc|c} B_1 & A_1 & X & \cdots & X & X \\ 0 & B_2 & A_2 & \cdots & X & X \\ \vdots & & \ddots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & B_{k-1} & A_{k-1} & X \\ \hline 0 & 0 & \cdots & 0 & B_k & A_k \end{array}\right] \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-db4cfa0ec23f03913864a3823ca46710_l3.png)
ここで,![]() は正整数,また
は正整数,また![]() のサイズを
のサイズを![]() とするとき(
とするとき(![]() ),つぎが成り立つ(
),つぎが成り立つ(![]() は横長の形状となり,行フルランクをもつ。また,
は横長の形状となり,行フルランクをもつ。また,![]() は横長で,行フルランクをもつ行列または零行列のどちらかである。)。
は横長で,行フルランクをもつ行列または零行列のどちらかである。)。
(25) ![]()
(26) ![]()
(27) ![]()
このとき,![]() が可制御対であるための必要十分条件は
が可制御対であるための必要十分条件は
条件C0: 式(24)において,![]()
が成り立つことである。また,![]() が可安定対であるための必要十分条件は、つぎが成り立つことである。
が可安定対であるための必要十分条件は、つぎが成り立つことである。
条件S0: 式(24)において,![]() のとき,
のとき,![]() は安定行列
は安定行列
——————————————————————————————————————–
![]() のとき,式(23)のような形式が得られていることは,式\(ref{eq3.4.3})の
のとき,式(23)のような形式が得られていることは,式\(ref{eq3.4.3})の![]() を上の
を上の![]() と読み替えれば明らかであろう。また,可安定性と可制御性と相違は,前者が
と読み替えれば明らかであろう。また,可安定性と可制御性と相違は,前者が![]() ばかりでなく
ばかりでなく![]() を許すところにあることに注意する。可制御性の条件C0と可安定性の条件S0の妥当性は,あとで示す。
を許すところにあることに注意する。可制御性の条件C0と可安定性の条件S0の妥当性は,あとで示す。
それでは,まず可制御性について,新しい条件を追加した定理を述べる。
——————————————————————————————————————–
定理 可制御性が成り立つための等価な条件
定義: 任意初期状態を,任意有限時間内に,任意状態に移動可能
条件C1: ![]()
条件C2: ![]()
条件C3: ![]() を選んで,
を選んで,![]() の固有値を任意に設定可能
の固有値を任意に設定可能
条件C4: ![]() (
(![]() は
は![]() のすべての固有値)
のすべての固有値)
条件C5: ![]() (
(![]() は
は![]() のすべての固有値)
のすべての固有値)
ここで,条件C4を満足する![]() の固有値
の固有値![]() は可制御固有値,満足しない固有値は不可制御固有値と呼ばれる。
は可制御固有値,満足しない固有値は不可制御固有値と呼ばれる。
——————————————————————————————————————–
前節までに,定義![]() 条件C1
条件C1![]() 条件C2
条件C2![]() 条件C3を示したので,以下では,条件C3
条件C3を示したので,以下では,条件C3![]() 条件C0
条件C0![]() 条件C4
条件C4![]() 条件C5
条件C5![]() 条件C2を示す。
条件C2を示す。
——————————————————————————————————————–
証明 <条件C3![]() 条件C0>
条件C0>
![]() とすると,式(24)を用いて
とすると,式(24)を用いて
(28) ![]()
となり,閉ループ系において![]() の固有値はそのまま残るが,C3に矛盾である。
の固有値はそのまま残るが,C3に矛盾である。
証明 <条件C0![]() 条件C4>
条件C4>
![]() を任意の複素数とする。
を任意の複素数とする。![]() に,式24を適用すると
に,式24を適用すると
(29) ![Rendered by QuickLaTeX.com \begin{equation*} \left[\begin{array}{c|cccc|c} B_1 & A_1-\lambda I_{m_1} & X & \cdots & X & X \\ 0 & B_2 & A_2-\lambda I_{m_2} & \cdots & X & X \\ \vdots & & \ddots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & B_{k-1} & A_{k-1}-\lambda I_{m_{k-1}} & X \\ \hline 0 & 0 & \cdots & 0 & B_k & A_k-\lambda I_{m_k} \end{array}\right] \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4a8adf165577c57e462e2e087bc9a257_l3.png)
を得る。ここで,![]() は横長の形状となり,行フルランク(行数に等しい階数)をもつので
は横長の形状となり,行フルランク(行数に等しい階数)をもつので
(30) ![]()
に,シルベスターの公式を適用して
(31) ![]()
を得る。この階数が![]() より小さくなるのは,式(29)から明らかなように,
より小さくなるのは,式(29)から明らかなように,![]() が
が![]() の固有値に等しい場合である。したがって,
の固有値に等しい場合である。したがって,![]() は
は![]() の固有値について調べれば十分である。すなわち,条件C4を得た。
の固有値について調べれば十分である。すなわち,条件C4を得た。
証明 <条件C4![]() 条件C5>
条件C5>
条件C4は,![]() を
を![]() 次元ベクトルとして
次元ベクトルとして
(32) ![]()
すなわち
(33) ![]()
と等価である。
証明 <条件C5![]() 条件C2>
条件C2>
条件C5より
(34) ![]()
を得て
(35) ![]()
が成り立つ。これは条件C2を意味する。
——————————————————————————————————————–
それでは,可安定性が成り立つための条件について考えよう。可制御であれば可安定であるので,問題は,不可制御で可安定の場合をどのように特徴付けるかである。不可制御であれば条件C0が不成立なので,![]() となり,
となり,![]() の固有値だけは状態フィードバックによってどうすることもできない。このとき可安定であるためには,
の固有値だけは状態フィードバックによってどうすることもできない。このとき可安定であるためには,![]() が安定行列であることを前提とするしかない。これは条件S0そのものであり,可安定性の条件としての妥当性が得られた。
が安定行列であることを前提とするしかない。これは条件S0そのものであり,可安定性の条件としての妥当性が得られた。
このことを踏まえて,可安定性の条件はつぎのように表される。
——————————————————————————————————————–
定理 可安定性が成り立つための等価な条件
定義 状態フィードバックにより安定化可能
条件S1: ![]() (
(![]() は
は![]() のすべての不安定固有値)
のすべての不安定固有値)
条件S2: ![]() \quad (〃)
\quad (〃)
証明 定義![]() 条件S0だから,条件S1
条件S0だから,条件S1![]() 条件S2との等価性を示せばよい。そのために,
条件S2との等価性を示せばよい。そのために,![]() のとき,式(29)の行列のランクが落ちるのは
のとき,式(29)の行列のランクが落ちるのは
(36) ![]()
(37) ![]()
の部分で,![]() が
が![]() の固有値に一致した場合である。したがって,条件S0を保証するためには,
の固有値に一致した場合である。したがって,条件S0を保証するためには,![]() に
に![]() のすべての不安定固有値を入れて,式(37)を調べ,列フルランクとなればよい。すなわち,条件C4
のすべての不安定固有値を入れて,式(37)を調べ,列フルランクとなればよい。すなわち,条件C4![]() 条件C5において,
条件C5において,![]() は
は![]() のすべての不安定固有値という条件をつければよい。
のすべての不安定固有値という条件をつければよい。
——————————————————————————————————————–
上の可制御性と可安定性のさまざまな条件のうち,理論展開では条件C5とS2が,数値計算では条件C0,C4と,条件S0,S1がよく用いられる(条件C5![]() 条件C4と条件S2
条件C4と条件S2![]() 条件S1による判定法は,PBH(Popov-Blevitch-Hautus)法と呼ばれる。)。
条件S1による判定法は,PBH(Popov-Blevitch-Hautus)法と呼ばれる。)。
例えば,可制御性は状態フィードバックにより不変であることを示そう。
——————————————————————————————————————–
定理 ![]() が可制御対ならば
が可制御対ならば![]() も可制御対である。
も可制御対である。
証明 条件C5より,任意の![]() に対して
に対して
(38) ![]()
成り立つので,これを仮定して
(39) ![]()
を示せばよい。実際,![]() より
より
(40) ![]()
を得るが,このような![]() は,仮定(38)より,
は,仮定(38)より,![]() でなければならない。
でなければならない。
——————————————————————————————————————–
2. 状態方程式から安定性を調べる
|
いま対象が物理的な釣り合いの状態にあるとき,何らかの原因でこれが乱されたとしよう。このとき,対象に働きかけて,元の物理的な釣り合いの状態に速やかに戻すことは,最も基本的な制御目的として知られている。もし,対象自身に復元力が備わっていて,元の状態に戻ろうとする性質があれば,対象は「安定」(正確には「漸近安定」)と呼ばれる。このことを状態方程式$\dot{x}=Ax+Bu$から,どのように調べるかが,本章のテーマである。
そのために,まず状態方程式を解くことから始める。その解は,与えられた入力のもとでの状態の時間的振る舞い,すなわち「時間応答」を表している。これは,「零入力応答」と「零状態応答」の和として表される。ここで,零入力応答とは,入力を零すなわち$u=0$として,初期状態$x(0)\ne0$から出発して得られる時間応答であり,零状態応答とは,初期状態$x(0)=0$のもとで適当な入力が与えられるときの時間応答である。対象が物理的な釣り合いの状態にあって,これが何らかの原因で乱されたときの時間的振る舞いは,零入力応答に対応する。そこで,1次系$\dot{x}=ax$に対しては,$a<0$ならば安定である,また,$n$次系$\dot{x}=Ax$に対しては,「正方行列$A$の固有値の実部がすべて負であるならば安定」と判定すればよいことを学ぶ。 一方,零状態応答の中で重要なのは「インパルス応答」と呼ばれるもので,これが与えられると,どのような入力が与えられても,たたみこみ積分を行って出力が求まることを理解してほしい。 |
1. 物理法則から状態方程式を導く
|
私たちが制御したい対象が物である場合,その振る舞いは物理法則により記述される。一般に,動的な振る舞いを表す物理法則は微分方程式で表される。微分方程式というと尻込みする人もいるかもしれないが,最初は,ニュートンの運動第2法則 さて,制御を行うには対象の動的な振る舞い(状態変数の時間変化)を観測することが必要であり,そのためにセンサが用いられる。ここで,現実には,すべての状態変数にセンサを配置できるわけではなく,通常は状態変数の一部がセンサにより観測される。センサにより観測される変数と状態変数の間の関係式を,制御対象の「出力方程式」と呼ぶ。 本章では,動的な振る舞いが連立線形微分方程式で記述されるいくつかの制御対象に対して,状態方程式と出力方程式をペアにした「状態空間表現」を求める。これを図示した「ブロック線図」は,計算機シミュレーションを行う際にも有用である。 |
1.1 状態空間表現の導出例
1.1.1 ペースメーカ
|
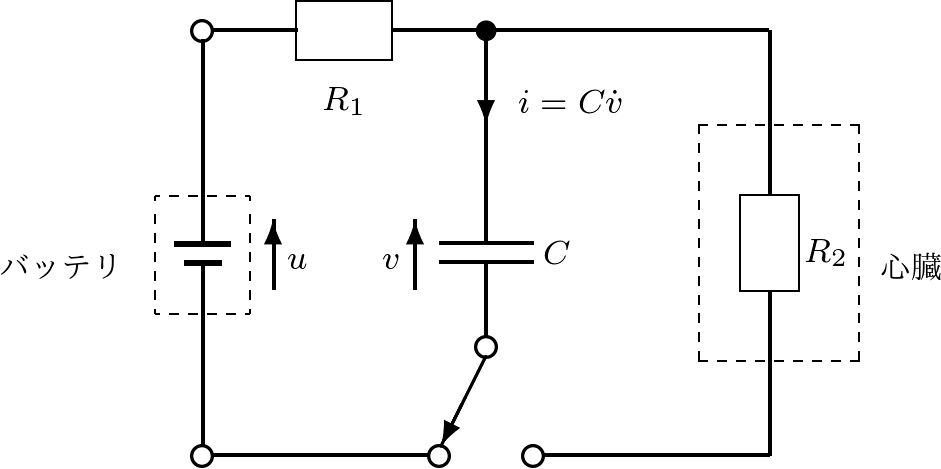
高齢化社会の到来に伴い,より優れた福祉・医療機器の開発が工学分野の大きなテーマの一つとなっている。図1.1に示すのは,心臓のペースメーカの簡単な原理図である。これは,まず左側の閉回路でコンデンサへの充電を行い,つぎにスイッチを切り替えてできる右側の閉回路で放電を行うという動作を周期的に繰り返すことにより,心臓のペースメーカの役割を果たそうとするものである。ここでは,状態方程式を導く最初の例として,このようなRC回路における充電と放電について考える。
そのために,キルヒホッフの電圧則より,左側閉回路と右側閉回路の回路方程式を考えると,それぞれ (1) (2) となる。ここで, (3) 状態方程式(3)を図1.2のように図示し,これを状態方程式に基づくブロック線図と呼ぶ。この描き方のポイントは,式(3)の右辺を表すのに加え合わせ記号○を用いることと,また 同様に,式(2)から得られる状態方程式は (4) であり,これによるブロック線図は図1.3のように示される。 (5) と与えられることはよいであろう(式(4)に代入して確かめよ)。状態方程式(4)は入力変数をもたないが,状態変数の初期値によって,状態変数の時間的振る舞いが現れる。この意味で,1次系(4)は シミュレーション1.1 式(5)で表されるコンデンサ電圧 (6) によって近似計算しなさい。 |
*系はsystemの訳語。ここでは「××システム」を簡潔に「××系」と書く。
**本書では,時間応答のコンピュータによるシミュレーション(simulation)の欄を設けた。最終的には時間応答の数学的理解が大切であるが,まずは,なぜそのような時間的振る舞いが現れるのかを物理的イメージをもって考えながら,典型的な時間応答に親しみをもってほしい。なお,本書の数値計算については演習問題の【4】を参照のこと。
1.1.2 教室のドア
教室で物の動きを実感できるものに,図1.5に示すようなばねとダンパ 図1.5 緩衝装置をつけたドア このドアの運動は回転運動であるが,話しをわかりやすくするため,図1.6に示すような等価な直線運動として調べてみよう。その出発点は,ニュートンの運動第2法則 (7) である。ここで, (8) のように表すことができる。ここで,ダンパが第1項の力を,ばねが第2項の力を与える。 (9) を得る。 (10) (11) のような1階の連立線形微分方程式で表される。これらを行列表示すると (12) のような状態方程式を得る (13) を得るセンサはあるが,ドアの速度を計測するセンサはないものとする。このとき, (14) 以上から,ドアに対して,状態方程式(12)と出力方程式(14)からなる2次系(second-order system)としての状態空間表現を得た。 シミュレーション 式(12)において,
|
*ばねとダンパの特性値を調整するためのねじを回すことにより行われる。
**本書では,![]() のように書いて,△を○で定義・表記する(△は○に等しいとする)。
のように書いて,△を○で定義・表記する(△は○に等しいとする)。
1.1.3 直流モータ
|
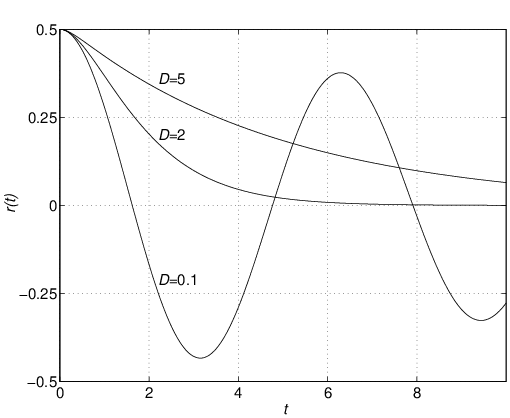
代表的なアクチュエータとしてモータがある。例えば図1.9に示すのは,ロボットアームを駆動する直流モータである。  図1.9 直流モータ このモデルは図1.10のように表される。 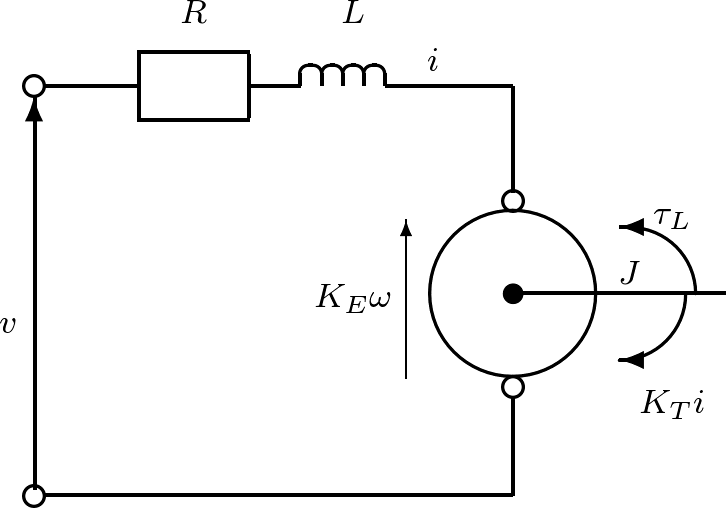 図1.10 直流モータのモデル このとき,つぎが成り立つ。 (15) (16) ここで,式(15)は機械系としての運動方程式であるが,電流による発生トルクの項 (17) (18) (19) のような状態方程式を得る。状態方程式(19)は二つの入力変数 (20) となる。このように,直流モータに対して,状態方程式(19)と出力方程式(20)からなる3次系(third-order system)としての状態空間表現を得た。つぎに一つのシミュレーション例を示す。 (21) で与えられ,上の例では (22) これから (23) (24) は直流モータの機械的時定数と呼ばれている。上の例で計算してみると (25) 式(19)と比較すると,状態空間表現の次数を1だけ減らしたことになる。 低次元化の過程を図1.12~図1.14に示しておく。 |
*式(18)は,式(19)のように物理パラメータどうしの演算を含まず,それらの変動の影響を考察するのに便利な形式であり,ディスクリプタ形式の状態方程式と呼ばれる。
**ここでは,2.1.3項で学ぶ時定数の知識を前提にしている。
1.2 状態空間表現へのモデリング
| 前節で述べた内容は,モデリング(modeling)という枠組でとらえられる。これは,何らかの対象に対して,目的に応じた科学的分析を通してそのモデルを得ようとするものである。私たちが扱う対象は,入力と出力をもつ動的システム 本書では,状態空間表現を次式のように書く。 (26) (27) ここで, |
*動的システムは,微分方程式・差分方程式のどちらで記述されるかによって連続時間系・離散時間系,重ね合わせの原理が成り立つか否かによって線形系・非線形系,常微分方程式か偏微分方程式かによって集中定数系・分布定数系,係数パラメータの時間依存性によって時変系・時不変系,入出力が確率過程であるか否かによって決定系・確率系などに分類される。
**非線形系の場合の取り扱いは7章で述べる。1~6章までは線形時不変系のみを扱う。
***他の数理モデルとして伝達関数表現がある。状態空間表現と伝達関数表現の間の相互関係については8章で述べる。
****他のアプローチとして,入力と出力の時系列データからモデリングを行うシステム同定がある。
1.3 状態空間表現の座標変換
| 状態空間表現を見やすくする一つの手段として,座標変換(coordinate transformation)があるので,これについて説明しよう。 いま, (28) (29) に対して,つぎの座標変換を行いたい。 (30) (31) に注意して (32) %すなわち (33) (34) となる。この結果を,参照しやすいようにつぎにまとめておく。 定理1.1 (35) (36) (37) 例題1.1 直流モータの状態方程式(25)において, (38) である。これに対して,座標変換 (39) を行うと,新しい状態方程式は (40) となることを示しなさい。 解答 座標変換後の (41) (42) のように得られる。 ここで,2次系の状態方程式が,二つの1次系の状態方程式 (43) に分離されており,入力から状態変数への影響の考察をしやすくなっていることに注意してほしい。 |
1.4 状態空間表現の直列結合
| 制御対象の状態空間表現を求める際に,図1.15に示すように,二つの部分システムの状態空間表現を求めておいて,これらを直列結合(serial connection)する場合がある。このときの結合システムの状態空間表現を求めることを考える。
まず,その結果を定理の形で示そう。 (44) (45) (46) (47) に対して, (48) (49) のように得られる。 証明 (50) (51) となる。第1式と (52) (53) に対して( (54) (55) を, 解答 定理1.2を用いて,直列結合の状態空間表現として (56) (57) が得られる 問1.4 例題1.2の直列結合の状態空間表現を,状態ベクトルが |
*ここで,![]() 行列の縦線と横線,
行列の縦線と横線,![]() 行列の横線は,状態ベクトルの要素
行列の横線は,状態ベクトルの要素![]() ,
,![]() のサイズに適合するように引かれている。
のサイズに適合するように引かれている。
演習問題
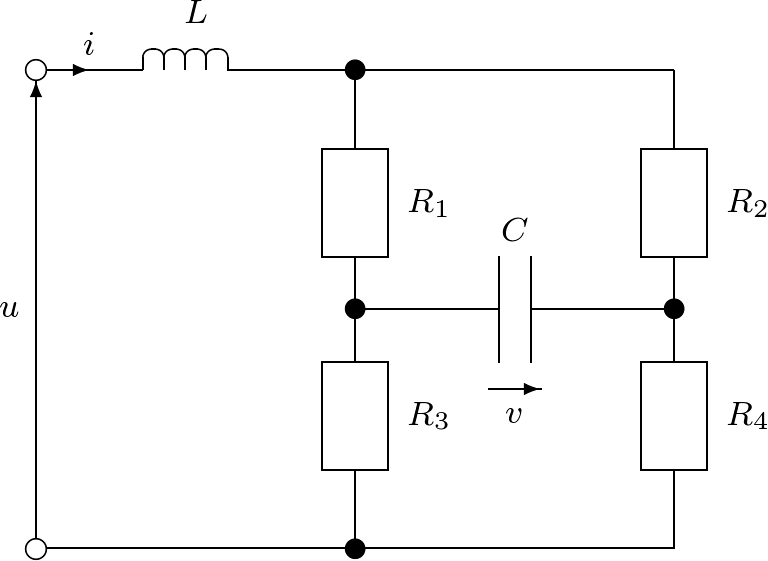
【1】 いろいろな計測装置の基礎となる電気回路の一つにブリッジ回路がある。 例えば,図1.16に示すブリッジ回路 (58) (59) で与えられる。いま,ブリッジ条件 (60) が成り立つとして,つぎの状態方程式を導出しなさい。 (61) この状態方程式に基づいて,平衡ブリッジ回路のブロック線図を描きなさい。
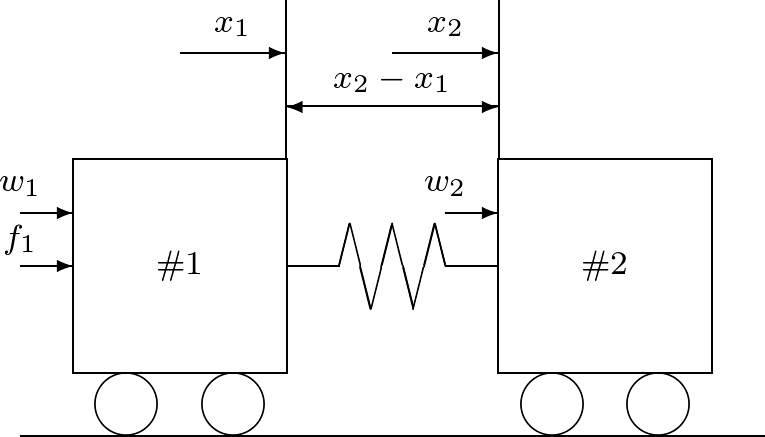
(62) (63) で与えられる。ここで, (64) この状態方程式に基づいて,連結台車のブロック線図を描きなさい。
MATLABとSIMULINKが手元にあれば,シミュレーション1.3と同一条件下で,直流モータの低次元化後の状態方程式25による角速度の応答を,低次元化前の状態方程式19によるものと比較しなさい。  図1.18 SIMULINKによる微分方程式のブロック表現 図1.18 SIMULINKによる微分方程式のブロック表現 |
*高橋・有本:回路網とシステム理論,コロナ社 (1974)のpp.65![]() 66から引用。
66から引用。
**B.Wie, D.2.Bernstein : Benchmark Problems for Robust Control Design, ACC Proc. pp.2047![]() 2048 (1992) から引用。
2048 (1992) から引用。
***The Student Edition of MATLAB-Version\,5 User’s Guide, Prentice Hall (1997)
****The Student Edition of SIMULINK-Version\,2 User’s Guide, Prentice Hall (1998)
![Rendered by QuickLaTeX.com \left[\begin{array}{c} \dot{x}_a(t) \\ \dot{x}(t) \end{array}\right]= \left[\begin{array}{c|cc} -\frac{1}{T_a} & 0 & 0 \\\hline 0 & 0 & 1\\ K\omega_n^2c_a & -\omega_n^2 & -2\zeta\omega_n \end{array}\right] \left[\begin{array}{c} x_a(t) \\ x(t) \end{array}\right]+ \left[\begin{array}{cc} \frac{K_a}{T_a} \\\hline 0 \\ 0 \end{array}\right] u(t)](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3dc93aa0d56d857eab79787359377985_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{ll} L\dot{i}(t)=-(\frac{R_1R_2}{R_1+R_2}+\frac{R_3R_4}{R_3+R_4})i(t)-(\frac{R_1}{R_1+R_2}-\frac{R_3}{R_3+R_4})v(t) +u(t) \\[1mm] C\dot{v}(t)=-(\frac{R_2}{R_1+R_2}-\frac{R_4}{R_3+R_4})i(t) -(\frac{1}{R_1+R_2}+\frac{1}{R_3+R_4})v(t)\\[1mm] \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-248343422f79de106349800ce8d3d914_l3.png)


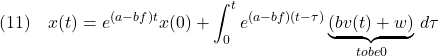
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \underbrace{ \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \end{array}\right] }_{\dot{x}_E(t)} = %\underbrace{ \left[\begin{array}{cc} a & 0 \\ 1 & 0 \end{array}\right] %}_{A_E} \underbrace{ \left[\begin{array}{c} x(t) \\ x_I(t) \end{array}\right] }_{x_E(t)} + %\underbrace{ \left[\begin{array}{c} b \\ 0 \end{array}\right] %}_{B_E} u(t) + \underbrace{ \left[\begin{array}{c} w \\ 0 \end{array}\right] }_{w_E} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ed7888e66cf423a299c78119493e2a8f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad u(t)=-fx(t) %\underbrace{ -f_Ix_I(t) %}_{+v(t)} =- \underbrace{ \left[\begin{array}{cc} f & f_I \end{array}\right] }_{F_E} \underbrace{ \left[\begin{array}{c} x(t) \\ x_I(t) \end{array}\right] }_{x_E(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5541d2dd02a7b6ebe166310f4c922b7f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \underbrace{ \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \end{array}\right] }_{\dot{x}_E(t)} = \underbrace{ \left[\begin{array}{cc} a-bf & -bf_I \\ 1 & 0 \end{array}\right] }_{A_{EF}} \underbrace{ \left[\begin{array}{c} x(t) \\ x_I(t) \end{array}\right] }_{x_E(t)} + \underbrace{ \left[\begin{array}{c} w \\ 0 \end{array}\right] }_{w_E} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9ce54a9bb373b31ef22c017c0033d328_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(23)\quad \left[\begin{array}{c} x(t) \\ x_I(t) \end{array}\right] \ \rightarrow\ \left[\begin{array}{c} 0 \\ \displaystyle{\frac{w}{bf_I}} \end{array}\right] \quad (t\rightarrow\infty) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-730cb6e0547a706ae11a604fcf3f76b4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(31)\quad %\underbrace{ \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \end{array}\right] %}_{\dot{x}_E(t)} = \underbrace{ \left[\begin{array}{cc} a-bf & -bf_I \\ 1 & 0 \end{array}\right] }_{A_{EF}} %\underbrace{ \left[\begin{array}{c} x(t) \\ x_I(t) \end{array}\right] %}_{x_E(t)} + %\underbrace{ \left[\begin{array}{c} w \\ -r \end{array}\right] %}_{w_E} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-107de515677af73c8cfa3d74309054d6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(32)\quad \left[\begin{array}{c} x(t) \\ x_I(t) \end{array}\right] \ \rightarrow\ \underbrace{ \displaystyle{\frac{1}{bf_I}} \left[\begin{array}{cc} 0 & bf_I \\ -1 & a-bf \end{array}\right] }_{A_{EF}^{-1}} \left[\begin{array}{c} -w \\ r \end{array}\right] \quad (t\rightarrow\infty) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d1efa2ea9c0128df30789fc39ea551f4_l3.png)
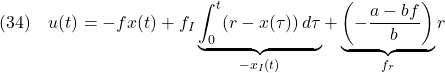
![Rendered by QuickLaTeX.com \displaystyle{(41)\quad {\rm rank}\, \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S}=n+m }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6d7d661fc9e59a3b704afda235a27be2_l3.png)
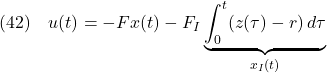
![Rendered by QuickLaTeX.com \displaystyle{(46)\quad %\underbrace{ \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \end{array}\right] %}_{\dot{x}_E(t)} = \underbrace{ \left[\begin{array}{cc} A-BF & -BF_I \\ C & 0 \end{array}\right] }_{A_{EF}} %\underbrace{ \left[\begin{array}{c} x(t) \\ x_I(t) \end{array}\right] %}_{x_E(t)} + %\underbrace{ \left[\begin{array}{c} w \\ -r \end{array}\right] %}_{w_E} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-eae149cb8e48771ddf2829382730be8f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(47)\quad A_{EF} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} - \left[\begin{array}{cc} B \\ 0 \end{array}\right] \left[\begin{array}{cc} F & F_I+I_m \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bdd5074b66a5f1df70acdb96f25154a5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(48)\quad \begin{array}{ll} A_{EF}^{-1} =& S^{-1}+ S^{-1} \left[\begin{array}{cc} B \\ 0 \end{array}\right] \left(I_m- \left[\begin{array}{cc} F & F_I+I_m \end{array}\right] S^{-1} \left[\begin{array}{cc} B \\ 0 \end{array}\right] \right)^{-1} \\[5mm] &\times \left[\begin{array}{cc} F & F_I+I_m \end{array}\right] S^{-1} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9d2c5a73b40a6bad18b71d793037dc0d_l3.png)
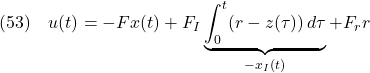
![Rendered by QuickLaTeX.com \displaystyle{(58)\quad \begin{array}{rl} \left[\begin{array}{c} \dot{\hat{x}}(t) \\ \dot{x}_I(t) \end{array}\right] =& \underbrace{ \left[\begin{array}{cc} A-HC_M-BF & -BF_I \\ 0(m\times n) & 0(m\times m) \end{array}\right] }_{A_K} \left[\begin{array}{c} \hat{x}(t) \\ x_I(t) \end{array}\right]\\[10mm] &+ \underbrace{ \left[\begin{array}{cc} H & 0(n\times m)\\ C_S & -I_m \end{array}\right] }_{B_K} \left[\begin{array}{c} y(t) \\ r \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0674921b2ea4d9a7a9554aeb4e94375f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(59)\quad u(t)= \underbrace{- \left[\begin{array}{cc} F & F_I \end{array}\right] }_{C_K} \left[\begin{array}{c} \hat{x}(t) \\ x_I(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1eaa990f79c14f18c22d28baecc3287b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(61)\quad \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \\ \dot{\hat{x}}(t) \end{array}\right] = \left[\begin{array}{ccc} A & -BF_I & -BF \\ C & 0 & 0 \\ HC_M & -BF_I & A-HC_M-BF \end{array}\right] \left[\begin{array}{c} x(t) \\ x_I(t) \\ \hat{x}(t) \end{array}\right] + \left[\begin{array}{c} w \\ -r \\ 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5628b37e548005d81b699f0317cfbcd2_l3.png)
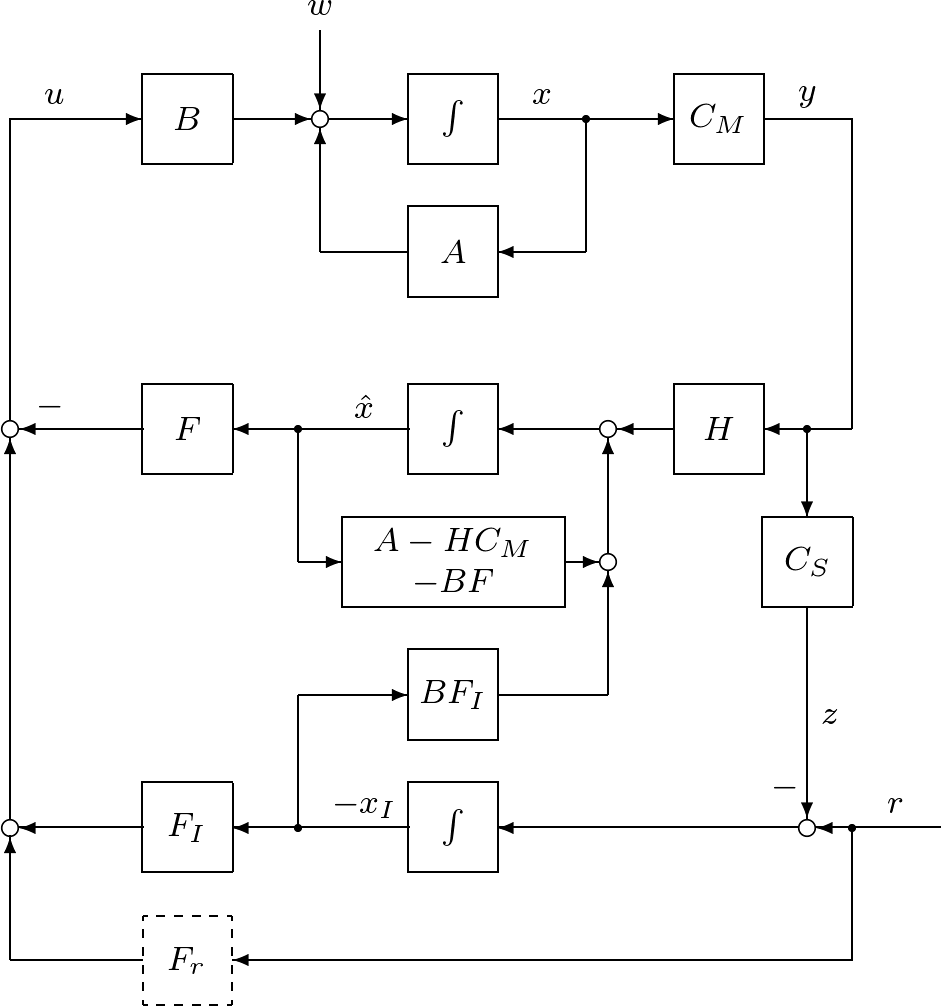
![Rendered by QuickLaTeX.com \displaystyle{(62)\quad \left[\begin{array}{c} x(t) \\ x_I(t) \\ e(t) \end{array}\right] = \left[\begin{array}{ccc} I_n & 0 & 0 \\ 0 & I_m & 0 \\ -I_n & 0 & I_n \end{array}\right] \left[\begin{array}{c} x(t) \\ x_I(t) \\ \hat{x}(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-398042fbd4912104fef837986adc51a1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(63)\quad \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \\\hline \dot{e}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc|c} A-BF & -BF_I & -BF \\ C & 0 & 0 \\\hline 0 & 0 & A-HC_M \end{array}\right] }_{ A_{EF}'= \left[\begin{array}{c|c} A_{EF} & - \left[\begin{array}{cc} B \\ 0 \end{array}\right] F \\[5mm] \hline 0 & \widehat{A} \end{array}\right] } \left[\begin{array}{c} x(t) \\ x_I(t) \\\hline e(t) \end{array}\right] + \left[\begin{array}{c} w \\ -r \\\hline -w \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b776ef380292f9c7b97e082e1356466d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(64)\quad \left[\begin{array}{c} x(t) \\ x_I(t) \\\hline e(t) \end{array}\right] \ \rightarrow\ \underbrace{ \left[\begin{array}{c|c} A_{EF}^{-1} & -A_{EF}^{-1} \left[\begin{array}{cc} B \\ 0 \end{array}\right] F\widehat{A}^{-1} \\[5mm]\hline 0 & \widehat{A}^{-1} \end{array}\right] }_{A_{EF}'\,^{-1}} \left[\begin{array}{c} -w \\ r \\\hline w \end{array}\right] \quad (t\rightarrow\infty) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3d3d576874ceeaf93880948df0adb803_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(69)\quad \frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] %}_{x_E(t)-x_{E\infty}} = \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E1}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] %}_{x_E(t)-x_{E\infty}} + \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E1}} (u(t)-u_\infty) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f6e3bc338005f728c3c6b147eb039e9e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(70)\quad \frac{d}{dt} %\underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] %}_{\dot{x}_E(t)} = \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E2}} %\underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] %}_{\dot{x}_E(t)} + \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E2}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-966078beee574786867caed4fcd2d943_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(71)\quad \left[\begin{array}{c} {\dot x}(t)-w \\ z(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \left[\begin{array}{c} x(t) \\ u(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1426f7e0895fd79de17dc34732b3e43c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(72)\quad \left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c1612c9c215faae7214a621c77652b77_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(73)\quad \frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} + \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-61e355172bd112774aad674a10e1d6b1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(74)\quad \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E2}} \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-47811d4d699fd4de1d937f73c0245ddb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(75)\quad \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E2}} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E3}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-46729c351e496ba40060fc93a706a112_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(76)\quad \underbrace{ \left[\begin{array}{cc} 0 & I_m \end{array}\right] }_{C_{E2}} \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} = \underbrace{ \left[\begin{array}{cc} C & 0 \end{array}\right] }_{C_{E3}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4ea560477a3448b751379c9a95240132_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(78)\quad \frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} + \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-40c26e612ca99e6fd4cd79c47fb7d193_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(80)\quad \int_0^\infty \left( \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right]^T Q_E \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] +{\dot u}^T(t)R_E{\dot u}(t)\right)\,dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-91e30617eef32873dec337f41b4b0942_l3.png)
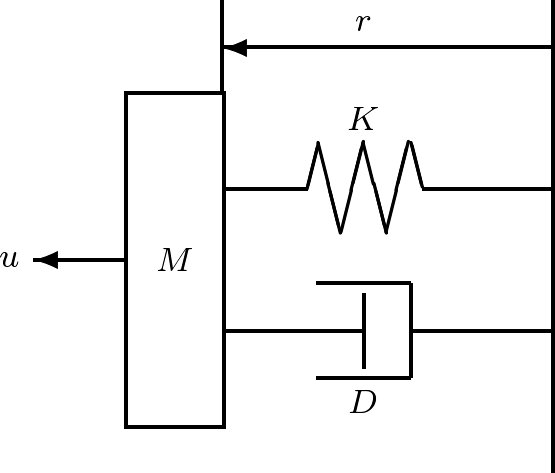
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{c} \dot{r}(t) \\ \dot{v}(t) \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\frac{K}{M} & -\frac{D}{M} \end{array}\right] }_A \underbrace{ \left[\begin{array}{c} r(t) \\ v(t) \end{array}\right] }_{x(t)}+ \underbrace{ \left[\begin{array}{c} 0 \\ \frac{1}{M} \end{array}\right] }_B u(t) \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1c7d500e812b8db8f7ef93fb748d863a_l3.png)
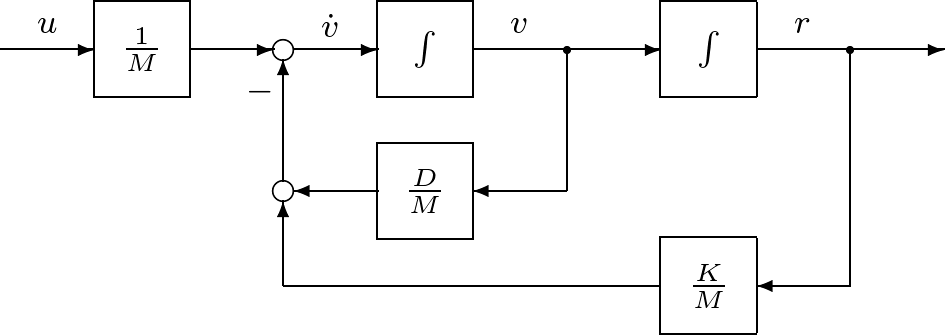
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{y_r(t)}_{y(t)}= \underbrace{ \left[\begin{array}{cc} c_r & 0 \end{array}\right] }_C \underbrace{ \left[\begin{array}{c} r(t) \\ v(t) \end{array}\right] }_{x(t)} \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ba917ead63a659449c7ce89833f94df6_l3.png)
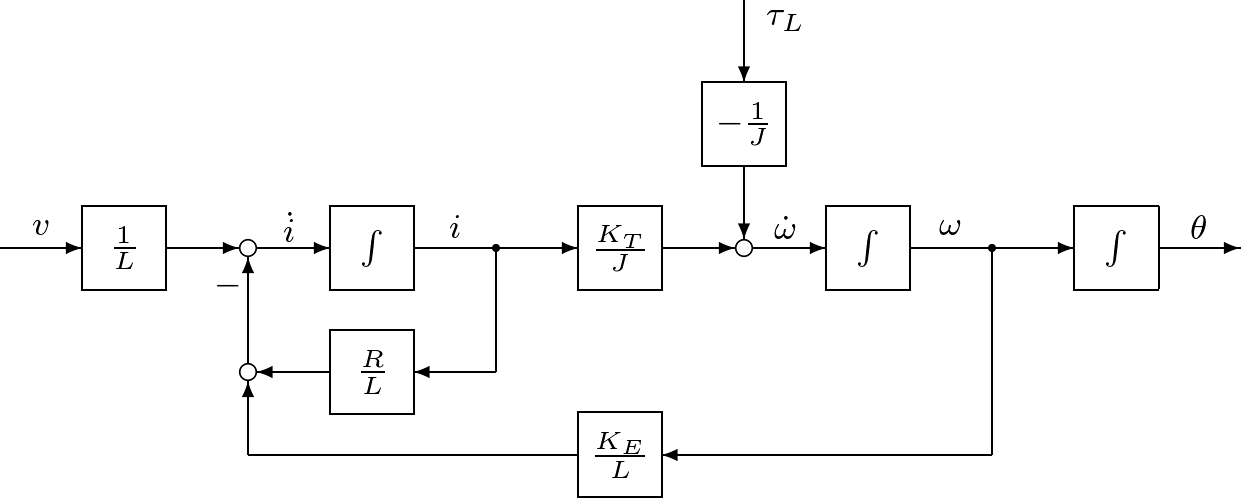
![Rendered by QuickLaTeX.com \begin{eqnarray*} %\begin{equation} %\renewcommand{\arraystretch}{1.3} %\begin{array}{rl} \underbrace{ \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & J & 0 \\ 0 & 0 & L \end{array}\right] }_{E} \left[\begin{array}{c} \dot{\theta}(t) \\ \dot{\omega}(t) \\ \dot{i}(t) \end{array}\right] & = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & K_T \\ 0 & -K_E & -R \end{array}\right] }_{A} \left[\begin{array}{c} \theta(t) \\ \omega(t) \\ i(t) \end{array}\right] \nonumber\\ & + \underbrace{ \left[\begin{array}{cc} 0 & 0 \\ 0 & -1 \\ 1 & 0 \end{array}\right] }_{B} \left[\begin{array}{cc} v(t) \\ \tau_L(t) \end{array}\right] %\end{array} %\end{equation} \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8c9f17ab2cf165ed53693c17a0d06a1b_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{c} \dot{\theta}(t) \\ \dot{\omega}(t) \\ \dot{i}(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & \frac{K_T}{J} \\ 0 & -\frac{K_E}{L} & -\frac{R}{L} \end{array}\right] }_{E^{-1}A} \underbrace{ \left[\begin{array}{c} \theta(t) \\ \omega(t) \\ i(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{cc} 0 & 0 \\ 0 & -\frac{1}{J} \\ \frac{1}{L} & 0 \end{array}\right] }_{E^{-1}B} \underbrace{ \left[\begin{array}{cc} v(t) \\ \tau_L(t) \end{array}\right] }_{u(t)} \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-26653bd3a6e2a14d2a2dd8ae426bf5f9_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{c} y_\theta(t) \\ y_\omega(t) \end{array}\right] }_{y(t)}= \underbrace{ \left[\begin{array}{ccc} c_\theta & 0 & 0 \\ 0 & c_\omega & 0 \end{array}\right] }_C \underbrace{ \left[\begin{array}{c} \theta(t) \\ \omega(t) \\ i(t) \end{array}\right] }_{x(t)} \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3d3a761f1082c0bb1c76cbac090b269d_l3.png)
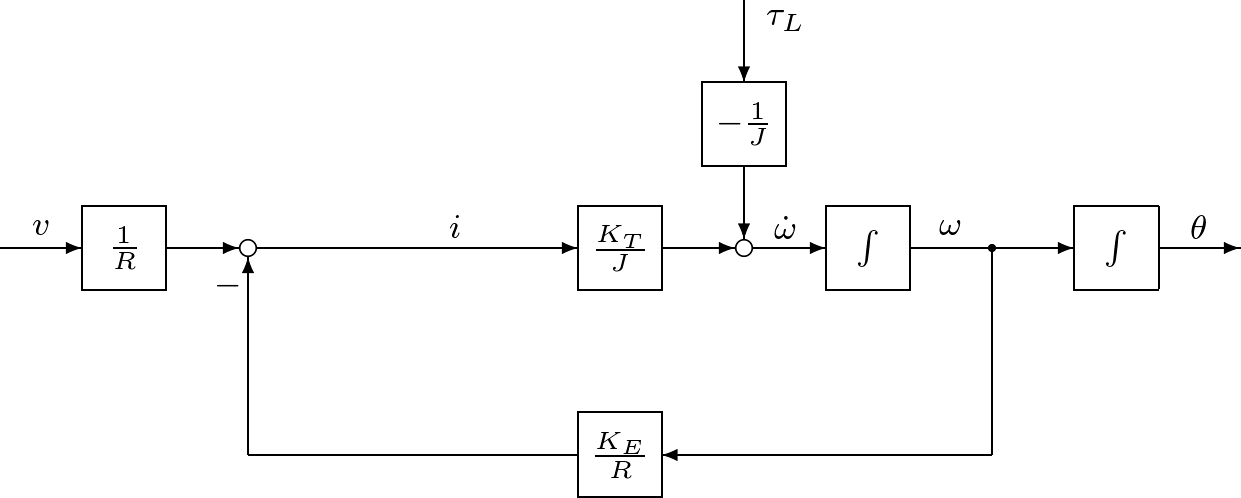
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{c} \dot{\theta}(t) \\ \dot{\omega}(t) \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & -\frac{1}{T_m} \end{array}\right] }_A \underbrace{ \left[\begin{array}{c} \theta(t) \\ \omega(t) \end{array}\right] }_{x(t)}+ \underbrace{ \left[\begin{array}{cc} 0 & 0 \\ \frac{1}{T_mK_E} & -\frac{1}{J} \end{array}\right] }_B \underbrace{ \left[\begin{array}{c} v(t)\\ \tau_L(t) \end{array}\right] }_{u(t)} \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b6118b470740014f12ba99fab45c5044_l3.png)
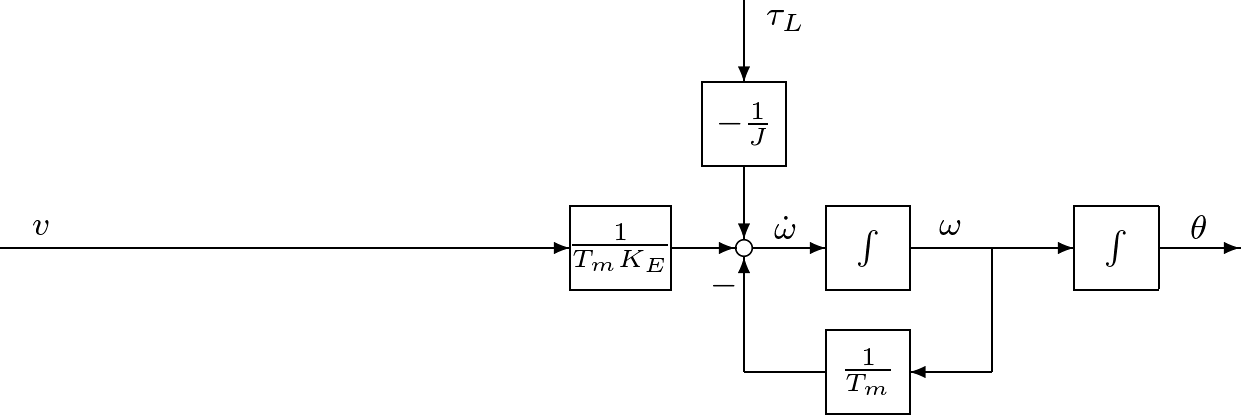
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{c} \dot{\theta}(t)\\ \dot{\omega}(t) \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & -\frac{1}{T_m} \end{array}\right] }_A \underbrace{ \left[\begin{array}{c} \theta(t)\\ \omega(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ \frac{1}{T_mK_E} \end{array}\right] }_B \underbrace{ v(t) }_{u(t)} % \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-06edd7a3c72279d04bbf853ea6c6bdd5_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{c} x'_1(t) \\ x'_2(t) \end{array}\right] }_{x'(t)} = \underbrace{ \left[\begin{array}{cc} 1 & T_m \\ 0 & -T_m \end{array}\right] }_T \underbrace{ \left[\begin{array}{c} \theta(t) \\ \omega(t) \end{array}\right] }_{x(t)} % \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c6eae3ed06b9f97fd4eaffb60d82c161_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{c} \dot{x}'_1(t) \\ \dot{x}'_2(t) \end{array}\right] }_{\dot{x}'(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 0 \\ 0 & -\frac{1}{T_m} \end{array}\right] }_{A'} \underbrace{ \left[\begin{array}{c} x'_1(t) \\ x'_2(t) \end{array}\right] }_{x'(t)} + \underbrace{ \left[\begin{array}{c} \frac{1}{K_E} \\ -\frac{1}{K_E} \end{array}\right] }_{B'} \underbrace{ v(t) }_{u(t)} \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e26ebb2f15db7052666007c6f7713109_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{cc} 1 & T_m \\ 0 & -T_m \end{array}\right] \left[\begin{array}{cc} 0 & 1 \\ 0 & -\frac{1}{T_m} \end{array}\right] \left[\begin{array}{cc} 1 & 1 \\ 0 & -\frac{1}{T_m} \end{array}\right] }_{TAT^{-1}} = \underbrace{ \left[\begin{array}{cc} 0 & 0 \\ 0 & -\frac{1}{T_m} \end{array}\right] }_{A'} \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-063430e3eba82786ff27bab3362214fe_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{cc} 1 & T_m \\ 0 & -T_m \end{array}\right] \left[\begin{array}{cc} 0 \\ \frac{1}{T_mK_E} \end{array}\right] }_{TB} = \underbrace{ \left[\begin{array}{c} \frac{1}{K_E} \\ -\frac{1}{K_E} \end{array}\right] }_{B'} \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-782f939b9de9db6e02c2932b3e39543c_l3.png)

![Rendered by QuickLaTeX.com \begin{equation*} \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_a(t) \end{array}\right]= \left[\begin{array}{cc|c} 0 & 1 & 0\\ -\omega_n^2 & -2\zeta\omega_n & K\omega_n^2 \\\hline 0 & 0 & -\frac{1}{T_a} \end{array}\right] \left[\begin{array}{c} x(t) \\ x_a(t) \end{array}\right]+ \left[\begin{array}{cc} 0 \\ 0 \\\hline \frac{K_a}{T_a} \end{array}\right] u_a(t) \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-375c43a38aaae14e657cf77df359e493_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{c} \dot{i}(t) \\ \dot{v}(t) \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} -\frac{1}{L}(\frac{R_1R_2}{R_1+R_2}+\frac{R_3R_4}{R_3+R_4})\ \ 0 \\ 0\ \ -\frac{1}{C}(\frac{1}{R_1+R_2}+\frac{1}{R_3+R_4}) \end{array}\right] }_A \underbrace{ \left[\begin{array}{c} i(t) \\ v(t) \end{array}\right] }_{x(t)}+ \underbrace{ \left[\begin{array}{c} \frac{1}{L} \\ 0 \end{array}\right] }_B u(t) \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a8387d56c5b1e0a5d7e4371a7c5bf88f_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \begin{array}{rcl} \underbrace{ \left[\begin{array}{c} \dot{x_1}(t) \\ \dot{x_2}(t) \\ \dot{v_1}(t) \\ \dot{v_2}(t) \end{array}\right] }_{\dot{x}(t)} &=& \underbrace{ \left[\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ -\frac{k}{m_1} & \frac{k}{m_1} & 0 & 0 \\ \frac{k}{m_2} & -\frac{k}{m_2} & 0 & 0 \end{array}\right] }_A \underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \\ v_1(t) \\ v_2(t) \end{array}\right] }_{x(t)} \\ & & \hspace*{-1zw} + \underbrace{ \left[\begin{array}{ccc} 0 & 0 & 0 \\ 0 & 0 & 0 \\ \frac{1}{m_1} & 0 & \frac{1}{m_1} \\ 0 & \frac{1}{m_2} & 0 \end{array}\right] }_B \underbrace{ \left[\begin{array}{c} w_1(t)\\ w_2(t)\\ f_1(t) \end{array}\right] }_{u(t)} \end{array} \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-726aaf73212dd3c34a1e3daca7912d95_l3.png)