状態空間表現
[C] 次のサイトも見ておこう。
[P] 柔軟構造物の状態空間表現は、状態変数の取り方がちょっと変わっているようだね。
[M] 常微分方程式ではなく、偏微分方程式を扱うようだね。
Home Work 2.3
[M] (2.22)がどのように出てくるのか、詳しく説明するね。その前に、(2.19)の![]() はベクトル値関数で、おそらくほとんどの人は初めて出会うものだと思うよ。この場合の
はベクトル値関数で、おそらくほとんどの人は初めて出会うものだと思うよ。この場合の![]() は2次元ベクトルなので、その要素を
は2次元ベクトルなので、その要素を![]() とすると
とすると
![]()
と書けるね。さらに、![]() は
は![]() の多変数関数なので
の多変数関数なので
![]()
と書けるね。ここで、![]() を
を![]() 周りでテーラー展開すると
周りでテーラー展開すると
![]()
ただし、![]() などの記法は
などの記法は
![]()
を表しているよ。![]() も同様に展開して
も同様に展開して
![]()
(3)と(5)を1次項で打ち切って、ベクトル表示したものが(2.22)ということになるね。
[P] 運動の各自由度について、位置と速度をペアにして状態変数を定義することが多いので、状態変数ベクトルの次元数は運動の自由度の2倍になるとと考えて良いようだね。
[C] 状態空間表現における行列![]() の呼び方に通称がないので、ちょっと困るよね。
の呼び方に通称がないので、ちょっと困るよね。
Flipped Classroom 2.3
[1] 行列![]() の(2,1)要素は
の(2,1)要素は
![]()
![]() のときが
のときが![]() 、
、![]() のときが
のときが![]() です。
です。
[2] MAXIMAの方は定義通りに計算しています。一方MATLABの方は次を参照してください。
Home Work 2.2
[M] (2.12)から(2.13)と(2.14)を得るところについて、説明するね。まず関数![]() の
の![]() の周りでのテーラー展開
の周りでのテーラー展開
![]()
に基づいて、次の![]() の1次近似を考えるんだ。
の1次近似を考えるんだ。
![]()
ここで、![]() 、
、![]() の場合を考えると
の場合を考えると
![]()
となるね。したがって、![]() の場合は
の場合は
![]()
また、![]() の場合は
の場合は
![]()
これらを(2.11)に代入したものが、それぞれ(2.13)と(2.14)です。
|
訂正 初版での記述「( |
[P] 剛体振り子ではの周期はどうやって求めればよいのだろう。Flipped Classroomで考えるようだね。
[C] 2つの平衡状態の物理的な振舞いが、(2.15)と(2.16)の相違とどう関係しているか興味があるね。
Flipped Classroom 2.2
[1] 単振り子の振舞いは(2.7)で決まります。一方、剛体振り子の振舞いは(2.15)で決まります。したがって、そこに現れる行列の(2,1)要素を等しいとおいてみます。
![]()
[2] 剛体振り子の長さ![]() の2/3の長さの単振り子を準備すれば、周期が一致すると考えられます。
の2/3の長さの単振り子を準備すれば、周期が一致すると考えられます。
Home Work 2.1
[P] 高校の物理で出てきた単振り子を「数学的振り子」と呼ぶことがあるんだ。知らなかった。「単」は「単一(single)」の意味かな?単振り子の周期は暗記させらたよね。
[M] その導出は一般には難しいけど、![]() が小さいときに限れば容易に理解できるな。線形理論の有用性を示す好例だね。
が小さいときに限れば容易に理解できるな。線形理論の有用性を示す好例だね。
[C] 一般の場合でも数値計算は簡単にできるんだ。微分方程式を解く関数は重宝するね。
Flipped Classroom 2.1
[1] (2.6)と(2.7)の表現が前提になっていることに注意してください。
[2] ![]() の場合の単振り子は考えにくいが、シミュレーションはとても興味深いです。「倒れるぞ!」という声が聞こえませんか?
の場合の単振り子は考えにくいが、シミュレーションはとても興味深いです。「倒れるぞ!」という声が聞こえませんか?
制御とは [P] 本書では、平衡状態周りの挙動の安定化を、制御の基本的役割と考えているようだね。各分野における平衡の概念については、ウィキペディアにまとめてあるよ。特に、「力学においては、物体に加わっている全ての力の合力と力のモーメントの和がともに 0 である状態を平衡と呼ぶ。」の記述があるね。 [M] 平衡状態を求めるには、速度変化が0、すなわち加速度=0を満たすものとして求めてよいようだ。この平衡状態まわりでテイラー展開した1次項までで、平衡状態周りの挙動は十分表されると仮定しているわけだ。だけど、展開する関数は、ベクトル値をとる多変数関数だから、ちょっと複雑に見えるかな。 [C] 昔、電気回路の洋書を読んだことがあって、平衡状態周りの挙動の解析のおかげで、かなりの工学の問題が解けて、大きな貢献してきたという記述を読んだことがあるよ。これが線形回路を学ぶ大きな意義だと強調していたことを覚えている。 (まだまだ多くの会話を書きとどめたいけど、先を急ぎます。) Home Work 1.3 [P] 来たー、アイサイト・ワールド! 位置だけでなく速度も零にしなければないので、「二兎を追うものは一兎も得ず」にならなければよいのだけど。 [M] (1.12)は と書けるので、2階の線形微分方程式を解けばよいのだけど、なんだか躊躇しているよね。微分方程式の教科書は見ないのかな? [C] 制御系設計の問題では、運動の自由度ごとに2階線形微分方程式が出てくるので、連立させる必要が出てくるため、後で示すようなもっとスマートな方法が必要になるらしいよ。 Flipped Classroom 1.3 [2] Home Work 1.2 [M] 制御則が(1.5)に変わっているけど、(1.1)に代入すると 左辺を右辺に移して と書けるね。停止制御の場合の [P] ここでも(1.5)をどうやって発生させるのかと思っていたら、どうもアクチュエータ(制御対象への働きかけを行う装置)の設置が前提になっているようだ。それならわかったよ。 [C] センサ(制御対象の情報収集装置)の設置も前提となっているようだ。すなわち、図1.3のように、センサで検出した信号 Flipped Classroom 1.2 [2] Home Work 1.1 [M] 数学的には(1.1)と(1.2)を合わせた、次の微分方程式を構成しているだけだよね。 というか、これを想定して(1.2)を決めているだけでは? [P] それはそうだけど、(1.2)は外力なので、力を発生する物理的装置が必要だよね。それはどうするの? [C] 普通のものつくりでは、(1)の左辺第2項を専用のデバイス(減衰器)で入れるのだけれど、アクチュエータという汎用のデバイスを用いて同様のことをさせているんだ。このことを魔法のように感じることができれば、制御に魅力に嵌ってしまうらしいよ。 Flipped Classroom 1.1 これが零となる時刻は [2] 各時刻における接線の傾きは、 接線の傾きはすべて負だから接線は右下がりで、しかもその傾きの絶対値は単調減少で零に近づいています。接線の傾きは速度の微分だから加速度を表し、これが(負の値を取りながら単調増加で)零に近づくということは滑らかな減速を意味しています。 [3] (3)より、基準となる時間 から、ゲインを 次のラグランジュの運動方程式を考えます。 ここで、運動エネルギー (1)のベクトル表示は次のように得られます。 左辺第1項は、次のように計算できます。 すなわち から、次式を得ます。 これより、CT14 補遺1
CT13 位置制御
![]()
[1] 数学的な解法の説明は抜きにしても、計算機で強引に解いていますね。でも重要なのは、モノを動かすときの速度パターン(増速・減速の三角形または台形カーブ)です。シミュレーションをしっかり目に焼き付けてください。![]() の値を徐々に大きくして、激突を避けられるぎりぎりの値を探してみてください。
の値を徐々に大きくして、激突を避けられるぎりぎりの値を探してみてください。CT12 速度制御
![]()
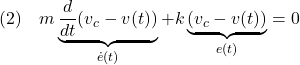
![]() において、
において、![]() が偏差
が偏差![]() に変わったとみなせま~す。
に変わったとみなせま~す。![]() を、アクチュエータに戻す仕組みが考えられており、これをフィードバックと呼ぶらしい。特に偏差
を、アクチュエータに戻す仕組みが考えられており、これをフィードバックと呼ぶらしい。特に偏差![]() を作るときに、検出した信号
を作るときに、検出した信号![]() にマイナスをつけるので、これを強調して、ネガティブ・フィードバックと呼ぶのだそうだ。これを友達に話すと、「制御という魔法をかけるのだからポジティブなフィードバックじゃないの」と来たよ。確かにそうだけど「ポジティブなフィードバックはネガティブなフィードバックなのだ!?」。
にマイナスをつけるので、これを強調して、ネガティブ・フィードバックと呼ぶのだそうだ。これを友達に話すと、「制御という魔法をかけるのだからポジティブなフィードバックじゃないの」と来たよ。確かにそうだけど「ポジティブなフィードバックはネガティブなフィードバックなのだ!?」。
[1] 微分方程式を解くにはどの関数を使うのか、また微分方程式をどのように定義するのかに注意してください。 ![]() をいろいろ変えてみてください。将来的には、アニメーションを作成できるとよいですね。次を参考にしてください。
をいろいろ変えてみてください。将来的には、アニメーションを作成できるとよいですね。次を参考にしてください。CT11 停止制御
![]()
[1] ![]() における接線の式は、傾き
における接線の式は、傾き![]() 、y切片
、y切片![]() だから
だから![]()
![]() となります。
となります。
![]() の5倍も経てば、十分零に近づいていることが確認できます。したがって
の5倍も経てば、十分零に近づいていることが確認できます。したがって![]()
![]() と決めます。
と決めます。ラグランジュの運動方程式
![]()
![]() とポテンシャル
とポテンシャル![]() を一般座標
を一般座標![]() と
と![]() で表し、ラグランジュ関数を
で表し、ラグランジュ関数を![]() とおいています。また、
とおいています。また、![]() は一般化力と呼ばれます。
は一般化力と呼ばれます。![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \frac{d}{dt} \underbrace{\left[\begin{array}{c} \frac{\partial L}{\partial\dot{q}_1}\\ \vdots\\ \frac{\partial L}{\partial\dot{q}_N} \end{array}\right]}_{\frac{\partial L}{\partial\dot{q}}} - \underbrace{\left[\begin{array}{c} \frac{\partial L}{\partial q_1}\\ \vdots\\ \frac{\partial L}{\partial q_N} \end{array}\right]}_{\frac{\partial L}{\partial q}} = \underbrace{\left[\begin{array}{c} Q_1\\ \vdots\\ Q_N \end{array}\right]}_{Q} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-aff94be67e7d9c457df32fe263479090_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \underbrace{\left[\begin{array}{c} \frac{\partial\frac{\partial L}{\partial\dot{q}_1}}{\partial\dot{q}_1}\ddot{q}_1+\cdots+\frac{\partial\frac{\partial L}{\partial\dot{q}_1}}{\partial\dot{q}_N}\ddot{q}_N\\ \vdots\\ \frac{\partial\frac{\partial L}{\partial\dot{q}_N}}{\partial\dot{q}_1}\ddot{q}_1+\cdots+\frac{\partial\frac{\partial L}{\partial\dot{q}_N}}{\partial\dot{q}_N}\ddot{q}_N \end{array}\right]}_{\frac{\partial}{\partial\dot{q}}(\frac{\partial L}{\partial\dot{q}}){\ddot{q}} } + \underbrace{\left[\begin{array}{c} \frac{\partial\frac{\partial L}{\partial q_1}}{\partial{q}_1}\dot{q}_1+\cdots+\frac{\partial\frac{\partial L}{\partial{q}_1}}{\partial q_N}\dot{q}_N\\ \vdots\\ \frac{\partial\frac{\partial L}{\partial q_N}}{\partial{q}_1}\dot{q}_1+\cdots+\frac{\partial\frac{\partial L}{\partial{q}_N}}{\partial q_N}\dot{q}_N \end{array}\right]}_{\frac{\partial}{\partial q}(\frac{\partial L}{\partial\dot{q}}){\dot{q}} } - \underbrace{\left[\begin{array}{c} \frac{\partial L}{\partial q_1}\\ \vdots\\ \frac{\partial L}{\partial q_N} \end{array}\right]}_{\frac{\partial L}{\partial q}} = \underbrace{\left[\begin{array}{c} Q_1\\ \vdots\\ Q_N \end{array}\right]}_{Q} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0ce26d3f68d56aa386be0d96d1e86d10_l3.png)
![]()
![]()
![]()
保護中: 例題