rcpsp41.py
|
|
|
|
|
|
|
|
【rcpsp41.csv】
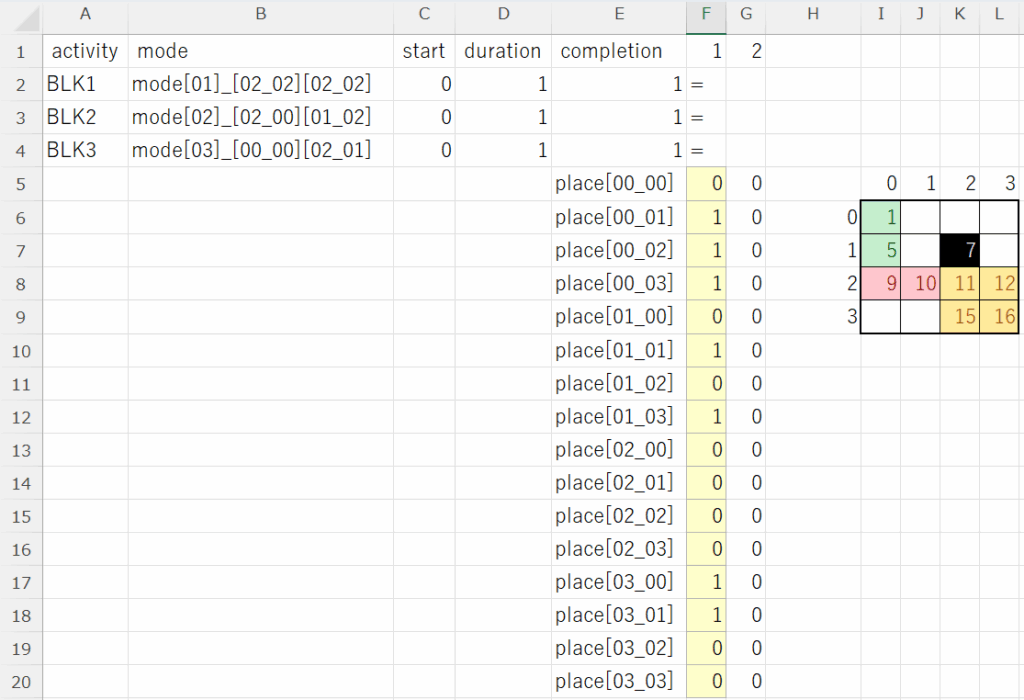
rcpsp41.py
|
|
|
|
|
|
|
|
【rcpsp41.csv】

optseq.pyの変更
startとcompletionを表示するには、次のようにoptseq.pyの3か所を変更します。
|
|
その1
|
|
その2
|
|
その3
|
|
rcpsp34.py
cace 1
|
|
これを実行すると次を得ます。
【rcpsp34.txt】
|
|
cace 2
|
|
これを実行すると次を得ます。
【rcpsp34.txt】
|
|
cace 3
|
|
これを実行すると次を得ます。
【rcpsp34.txt】
|
|
rcpsp35.py
|
|
場所取りを行う仮想アクティビティdactは、前後の搬入作業act[1]、搬出作業act[4]と「隙間なく」連結されています。これは不等式
![]()
![]()
![]()
![]()
が成り立つ、すなわち
![]()
![]()
を要求しているからです。
これを実行すると次を得ます。
【rcpsp35.txt】
|
|
いま、次のように24行と25行のコメントを外し、搬出作業日を固定します。
|
|
これを実行すると次を得ます。
【rcpsp35.txt】
|
|
rcpsp33.py
|
|
この部分を次のように書き換えます。行030の前で、1人で何日かかるかをperiodとして計算し、1人でperiod期間仕事をするようにスケジューリングを行って、そのあとで並列化を行っています。
|
|
これを実行すると次を得ます。
【rcpsp33.txt】
|
|
とても簡単に究極の平準化が行えると言えます。
rcpsp30.py
次はプッシュ型とプル型の結果を比べる簡単なプログラムですが、データセットの定義、アクティビティの定義(プッシュ型)、モードの付与(作業期間の指定)、求解からなる構成が見てとれます。
|
|
これを実行すると次を得ます。
【rcpsp30.txt】
|
|
納期日を10日とするプル型の結果を得るときは、
|
|
とします。納期日の前日まで作業を終わりたいので、duedateは納期日の前日としています。これを実行すると次を得ます。
【rcpsp30.txt】
|
|
rcpsp31.py
次はRCPSP法のプログラムの基本的な枠組みを示すプログラムで、アクティビティに先行制約が、モードに資源制約が組み込まれています。
|
|
データセットはPythonの辞書データとしています。keyでアクティビティを識別し、名前、作業期間、後続作業のリスト(後続がないときは0)、必要とするリソースなどからなるリストを対応させています。
|
|
データセットで定義された2つのアクティビティ(製作作業と納品作業)を定義しています。プル型のduedateは、2つとも納品作業のものを用いています。次に定義する先行関係があるので、納品作業は必ず製品作業が終わってから行うことになります。
|
|
プッシュ型計画を行うことも想定して、納期日は固定しています。これは2つの不等式
![]()
![]()
が成り立つ(![]() は完了日)、すなわち
は完了日)、すなわち![]() を要求しているからです。
を要求しているからです。
|
|
リソースのキャパシティは1です。各アクティビティについてモードは1個です。各モードは名前で区別します。
|
|
これを実行すると次の結果を得ます。
【rcpsp31.txt】
|
|
上のプログラムは、プッシュ型かプル型か、評価関数はメイクススパンか納期遅れ総和かで、4通りの実行ができます。それぞれの目的関数の値を確かめると参考になるかと思います。
rcpsp32.py
例題1をRCPSP法で解くプログラムを次に示します。
|
|
10個のアクティビティについてデータが定義されています。
|
|
プッシュ型の計画が想定されています。
|
|
先行関係は13個あります。
|
|
リソースのキャパシティは10です。各アクティビティについてモードは1個です。
|
|
これを実行すると次の結果を得ます。
【rcpsp32.txt】
|
|
[1] 例題1(図1.1)へのカレンダー挿入(図2.19の作成)
工程’sファイル「例題1.kzd」をコピーして、「ex1.kdz」とします。その編集期間とカレンダー(0:デフォールト)を次のように変更します。
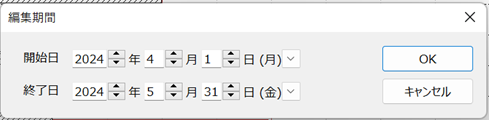
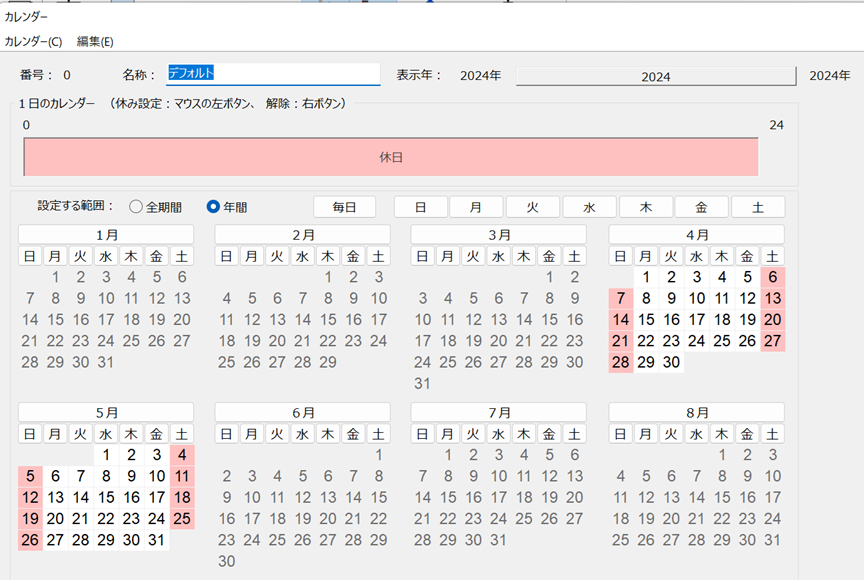
カレンダーを上書きすると、次が得られます。

ここで先行関係を整えるために、「日程調整」
を行うと、次が得られます。
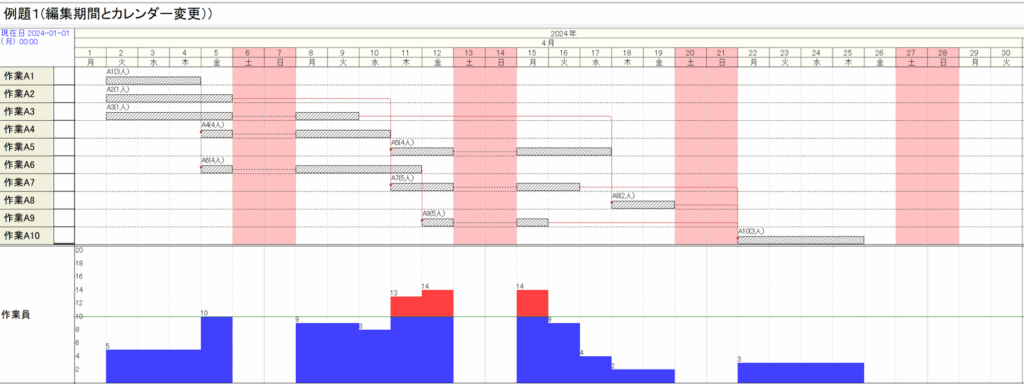
[2] 図2.12へのカレンダー挿入(図2.20の作成)
工程’sファイル「例題1a (開始日を10日シフト).kzd」をコピーして、「ex2.kdz」とします。その編集期間とカレンダー(0:デフォールト)をex1.kdzと同じように変更します。カレンダーを上書きすると、次が得られます。
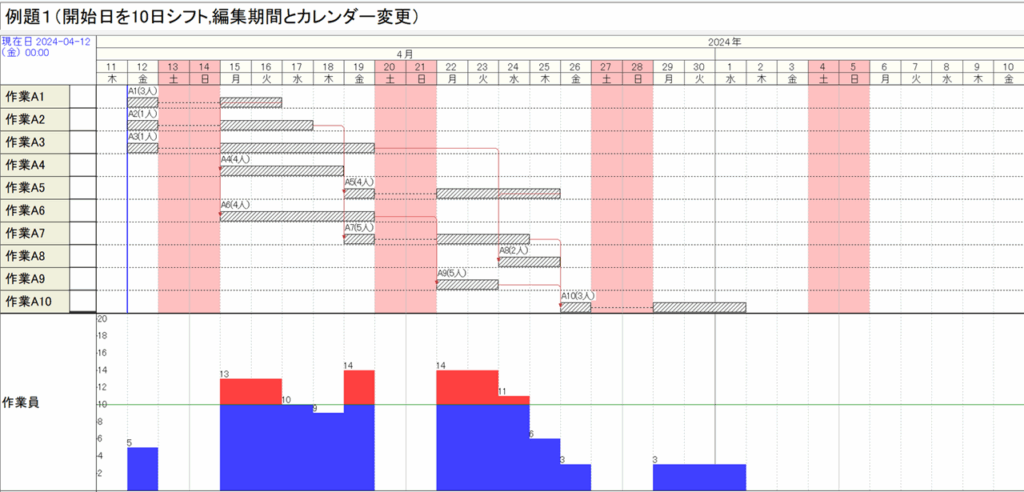
ここで先行関係を整えるために、「日程調整」を行うと、次が得られます。

[3] 図2.13へのカレンダー挿入(図2.21の作成)
工程’sファイル「例題1b (2つの計画を並べる).kzd」をコピーして、「ex3.kdz」とします。そのカレンダー(0:デフォールト)と同じように変更します。カレンダーを上書きすると、次が得られます。
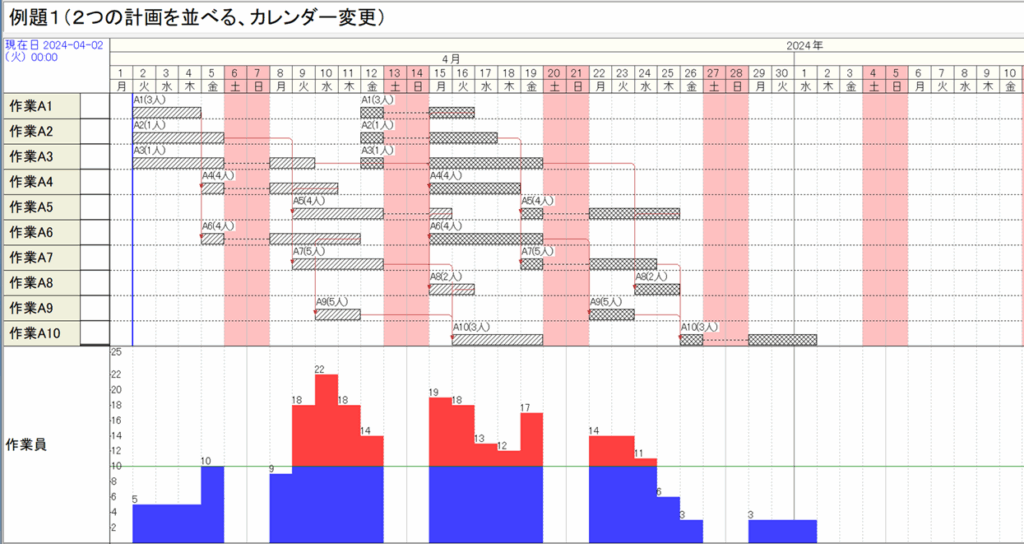
いま、コピーされた計画の先頭の3つのアクティビティについて、日程調整をかけても移動させない指定を行います(バーの右上にマークが表示されます)。
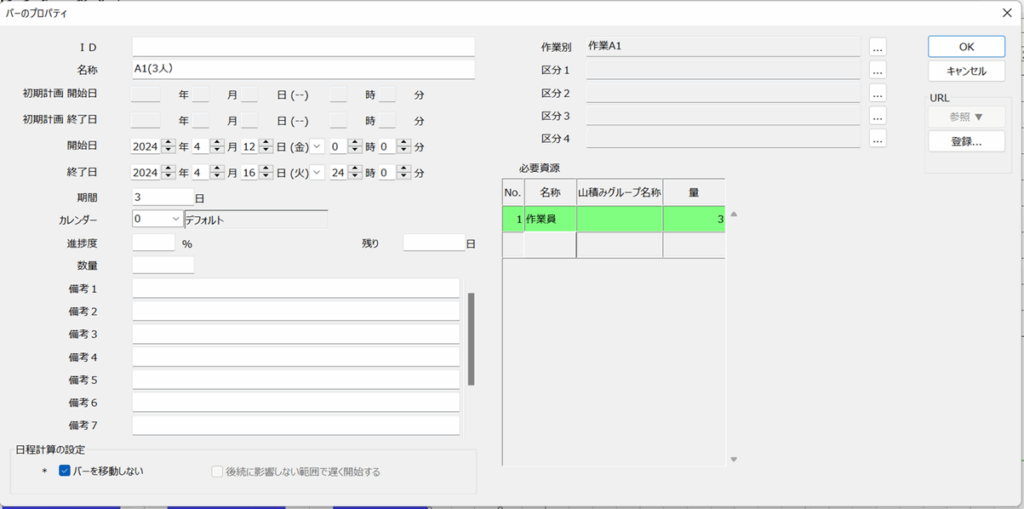
ここで先行関係を整えるために、「日程調整」を行うと、次が得られます。
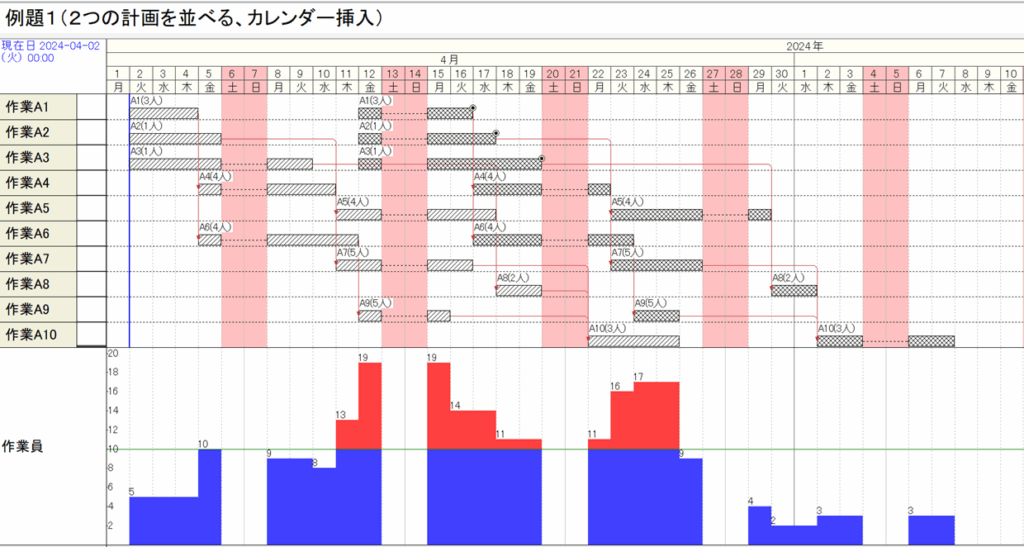
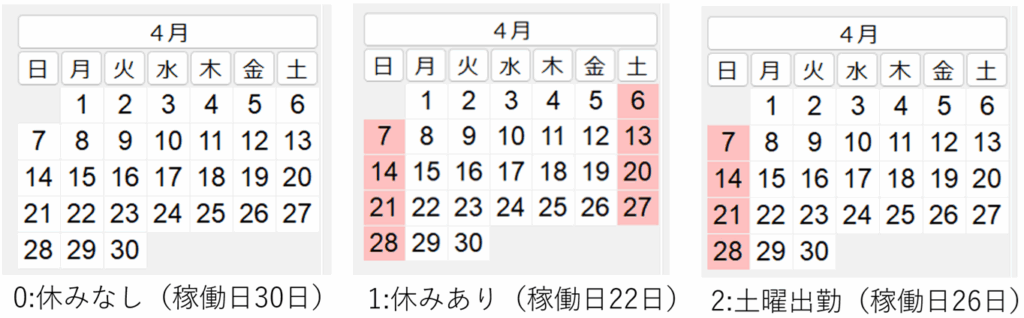
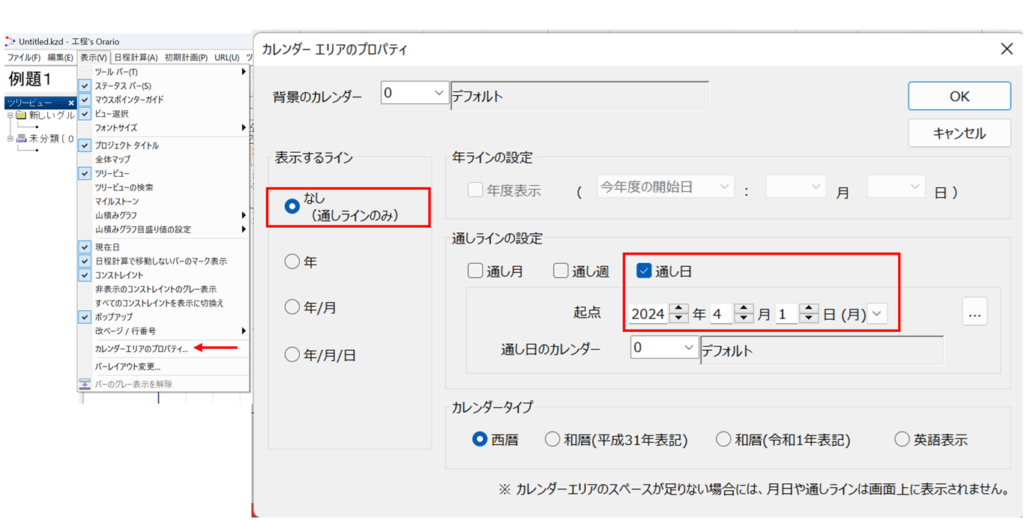
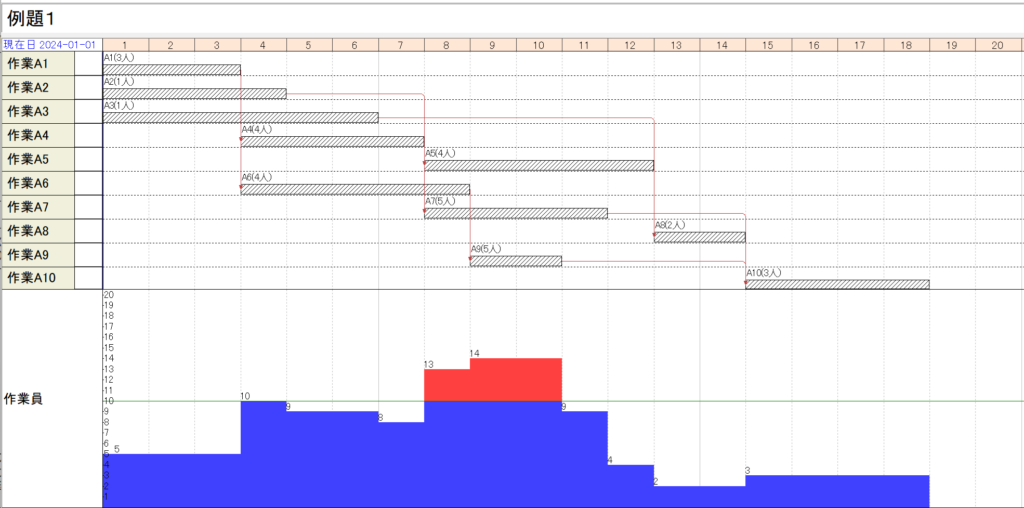
一般に、計画は稼働日を用いて行い、あとで非稼働日を挿入します。 [1]カレンダー 例題1に、休みなし、休みあり、土曜出勤も3種類のカレンダーを付与します。 [2]通し日 工程’sでは稼働日にシリアル番号を振った「通し日」の設定できます。 通し日の設定 第1章の例題1を通し日を用いて表すと次のようになります。
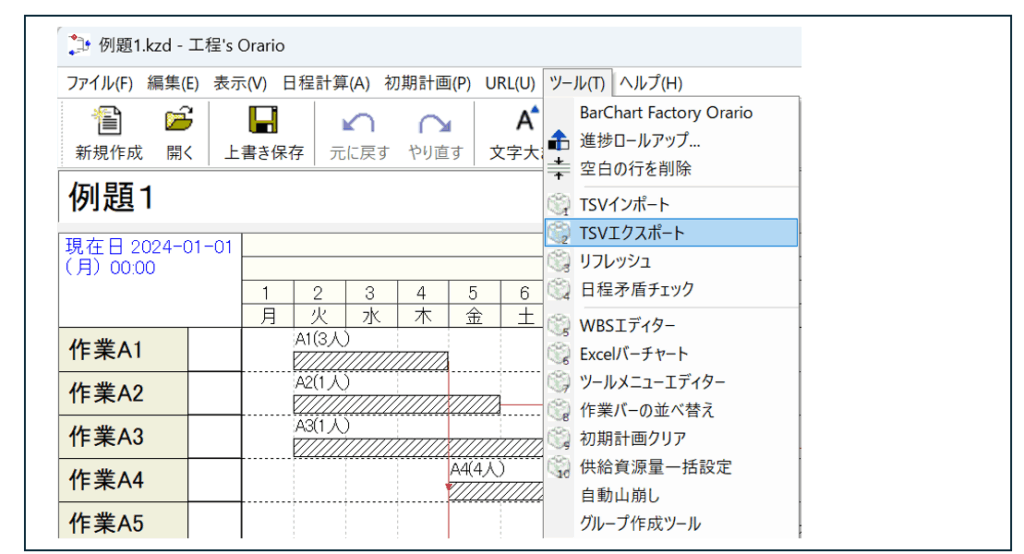
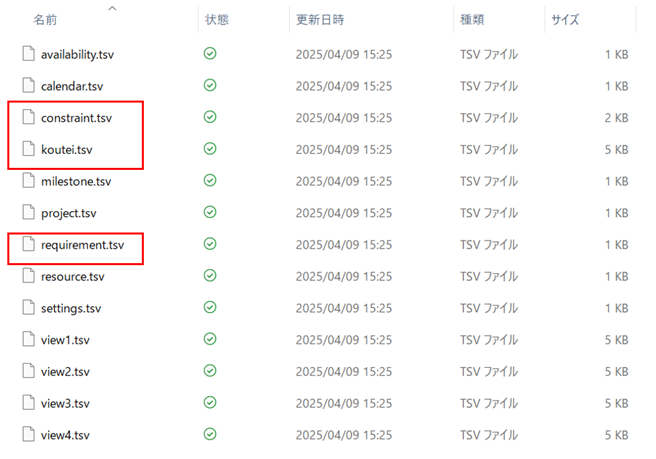
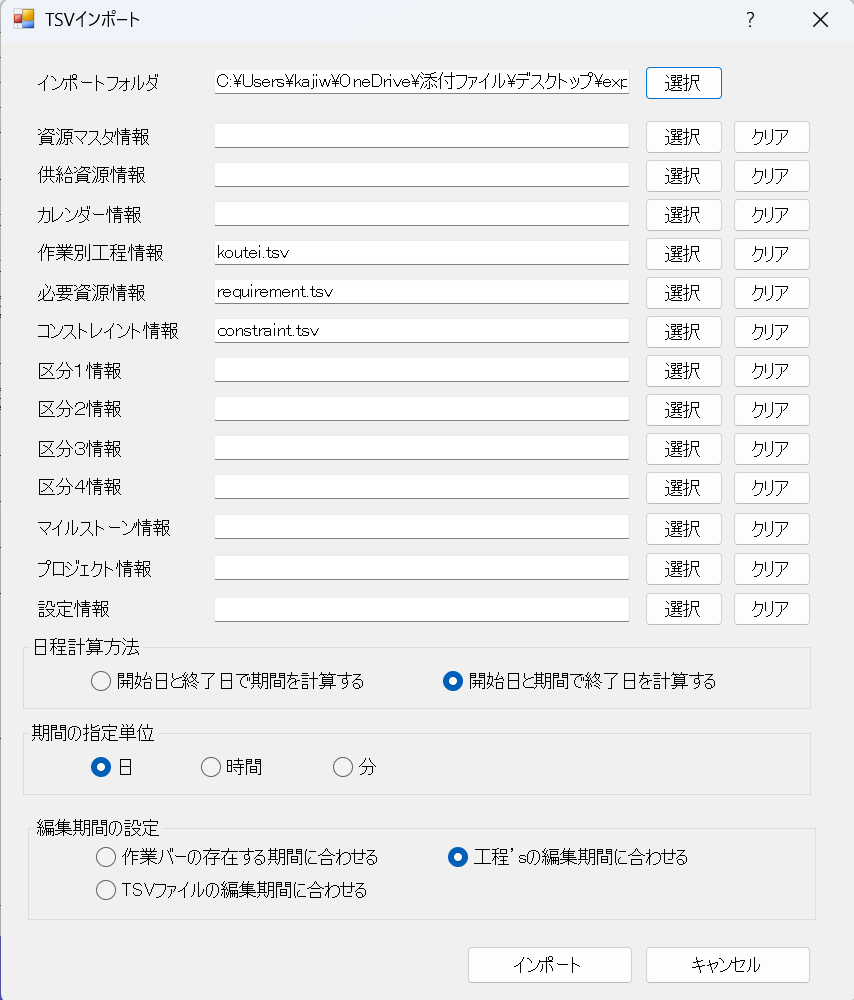
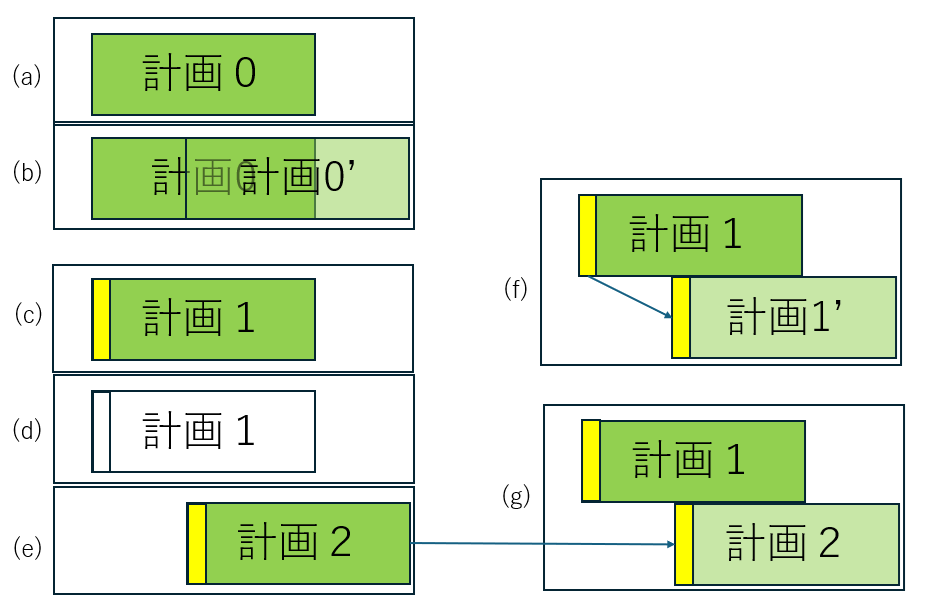
[1] エクスポート・インポート機能 「工程’s」にはオプションで、エクスポート・インポート機能があって、工程データを12種類のTSV(Tab Separated Values)ファイルに出力できます。 例題1.kzdに対してエクスポートをかけます。 この操作を行うと、指定したフォルダに次のように13種類のtsvファイルが作成されます。 ここで重要なのが赤枠で囲んだ3つのファイルで、koutes.tsv、constraint.tsv、requirement.tsvはそれぞれ日程計画、先行制約、資源制約に関する情報を含んでいます。 tsvファイルを、EXCELにdrag-dropすれば、簡単に中身をチェックできます。いま適当に編集してtsvファイルに戻したとします。これらを次のようにインポートすれば、例題1.kzdが変更されます。 [2] テンプレート 一つの計画を再利用したい場面はいろいろ考えられます。「工程’s」では通常の.kzdファイルのほかに、テンプレートファイル.kzt出力して、これを再利用することができます。 [3] 工程’sファイルの複製 計画期間が重なる2つの計画に対して山積み行って、リソースの不足がないかをチェックしたい場合があります。この目的のために次図を考えます。 まず、(a)は元ファイル(たとえば「例題1.kzd」)とします。同じ計画を一定期間おいて繰り返す場合は、(b)のように全部のアクティビティを選択してコピーすればOKです。これは「工程’s」の編集操作の範囲内で行うもので、おのずとアクティビティの数が限られます。 次に、(c)は(a)のすべてのアクティビティを一括して扱うために、最上位のグループ(黄色のバー)を設置した様子を表しています。具体的には次図となります。 これを一定期間ずらした計画との山積みの重複の様子を見るには、最上位のグループをコピーして、(f)のようにその下にペーストします。これは同一ファイル内の操作になります。 一方、(c)からテンプレートファイルを(d)のように作成し、これを一定期間ずらして読み込んで、もう一つの計画(e)を作成しておきます。一方のファイルの最上位のグループをコピーして、(g)のように他方のファイルの中でペーストします。これは2つの異なるファイル間の操作になります。ここで、2つのファイルは全く別の計画(別のテンプレートから作成された計画)でもよいことに注意してください。
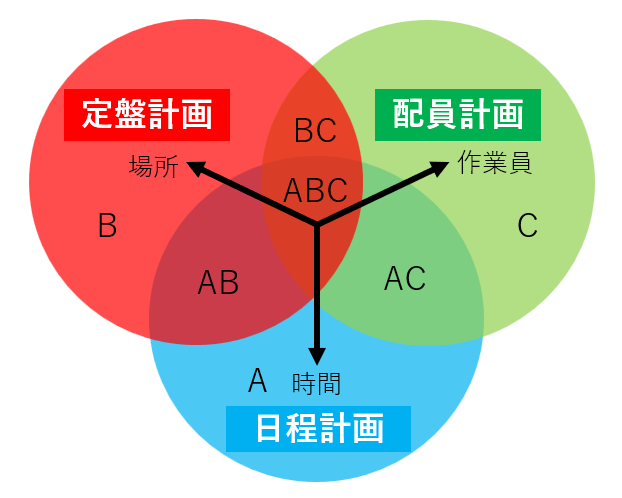
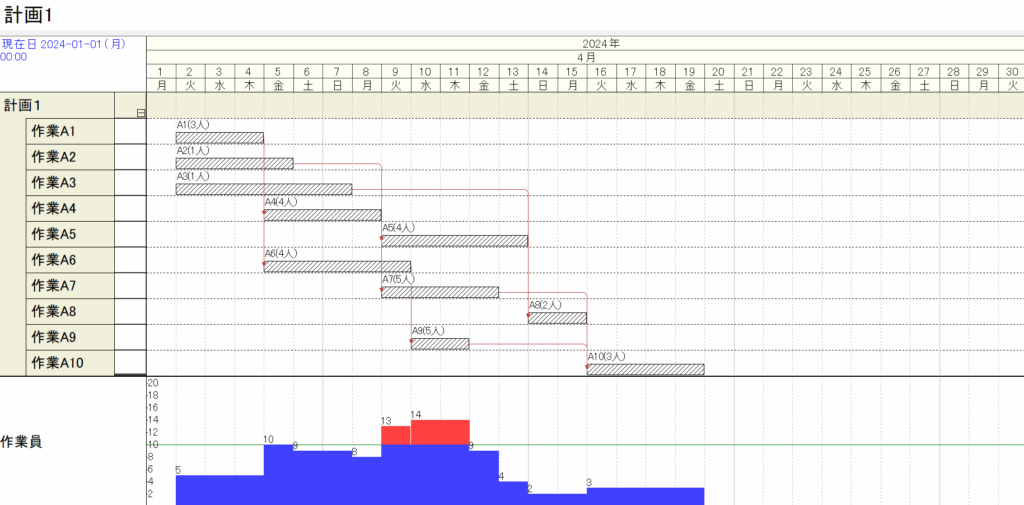
第1章の例題1を「工程’s」を用いてstep-by-stepで作成してみます。 [1]準備 [2]リソースの定義 [3]アクティビティの定義 アクティビティバーの設置 [4]先行制約の定義 – 山積みグラフの表示 造船工程計画 造船工程計画とは、ブロック製作のために2種類のリソース(場所、作業員)のタイムライン化(時間軸に並べること)と言えます。2つの計画AB,ACは比較的簡単に求まりますが、この2つを共通の日程で作成するのは簡単なことではありません。「二兎を追う者は一兎をも得ず」という諺がありますが、造船工程計画の困難性もそのような状況かもしれません。カレンダーと通し日
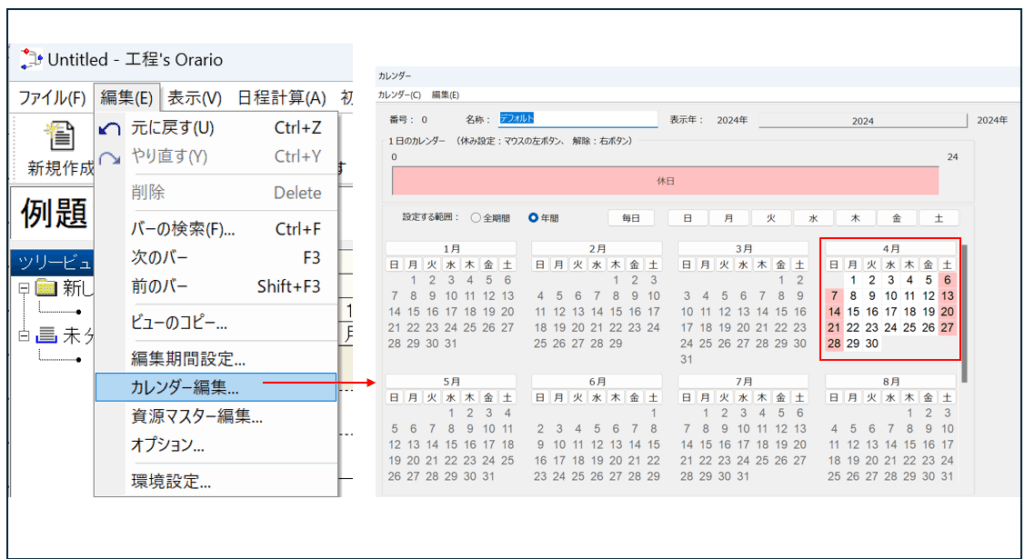
カレンダー編集
データセットの作成支援
「工程’s」の基礎
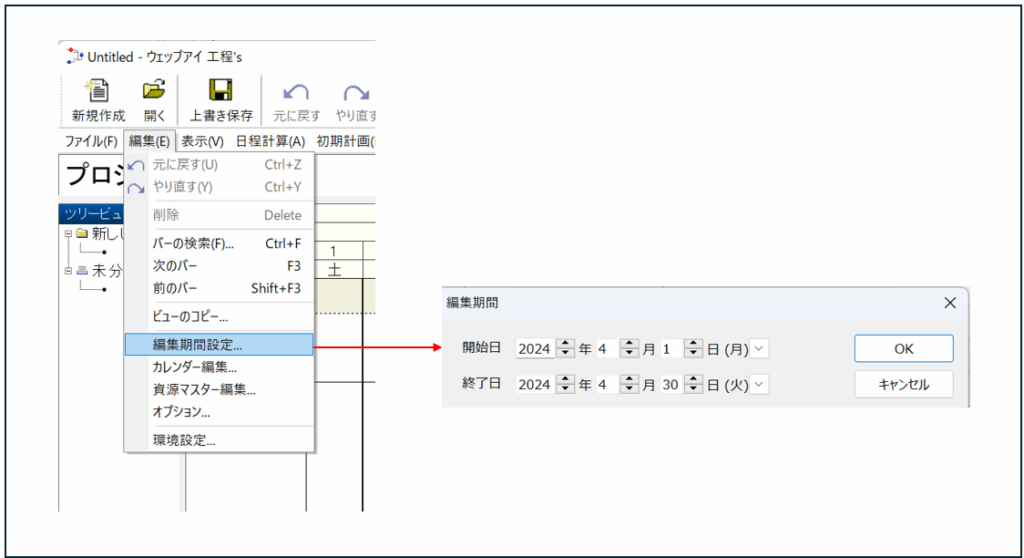
編集期間設定
現在日の設定
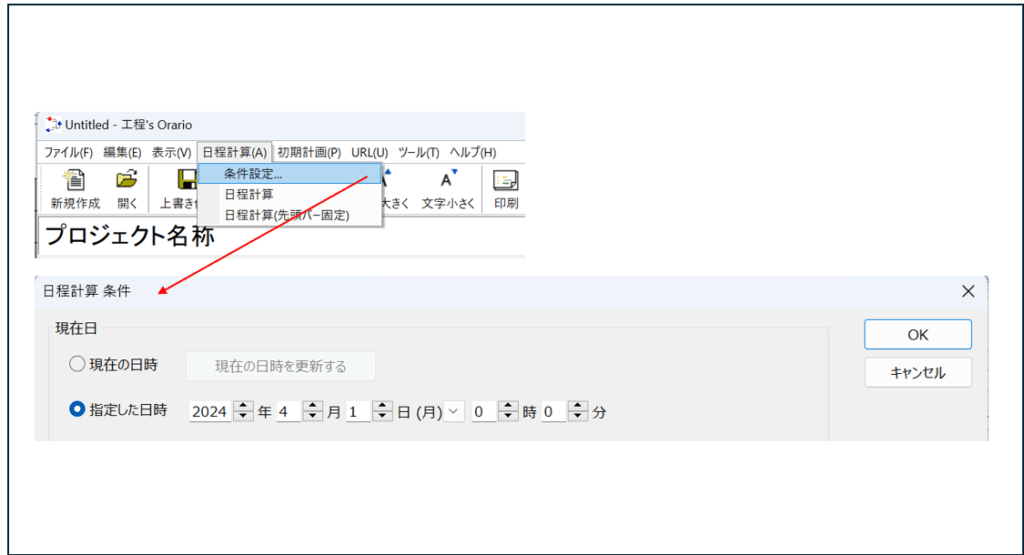
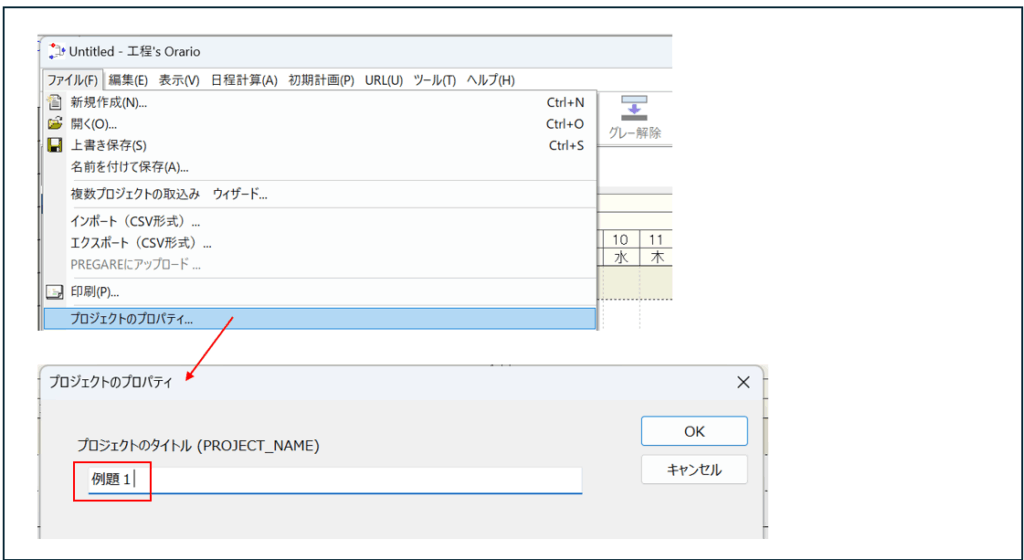
プロジェクト名称の設定
カレンダー編集(略)
通し日の設定(略)
資源マスター編集
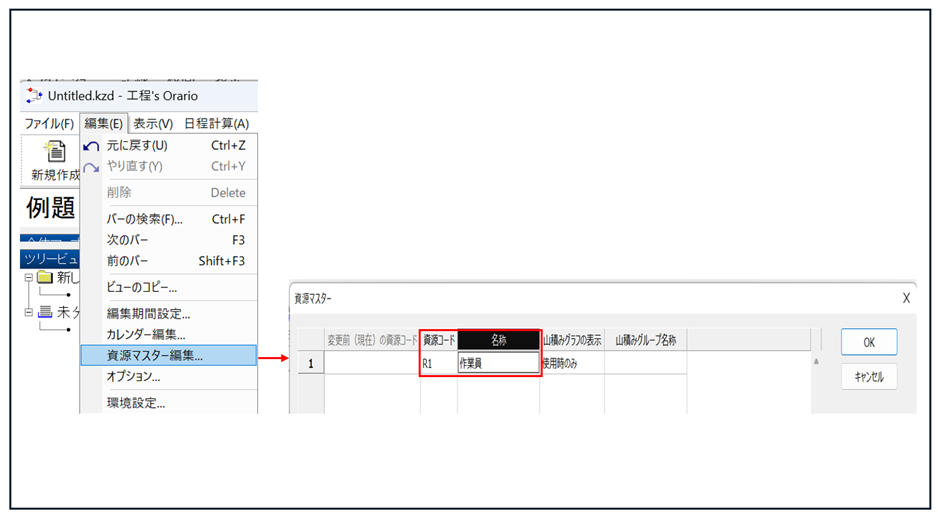
WBSの設定
– グループの挿入
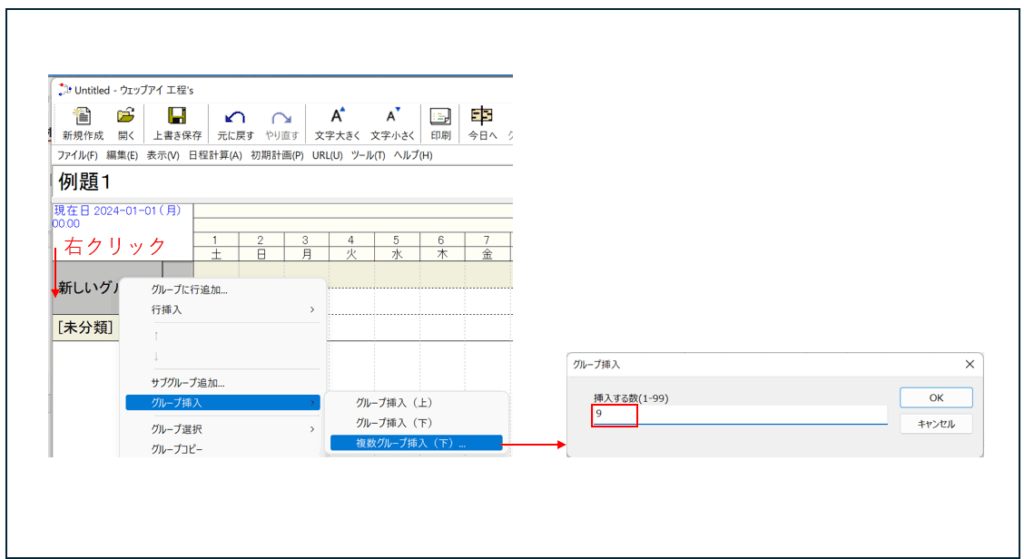
– グループプロパティの設定
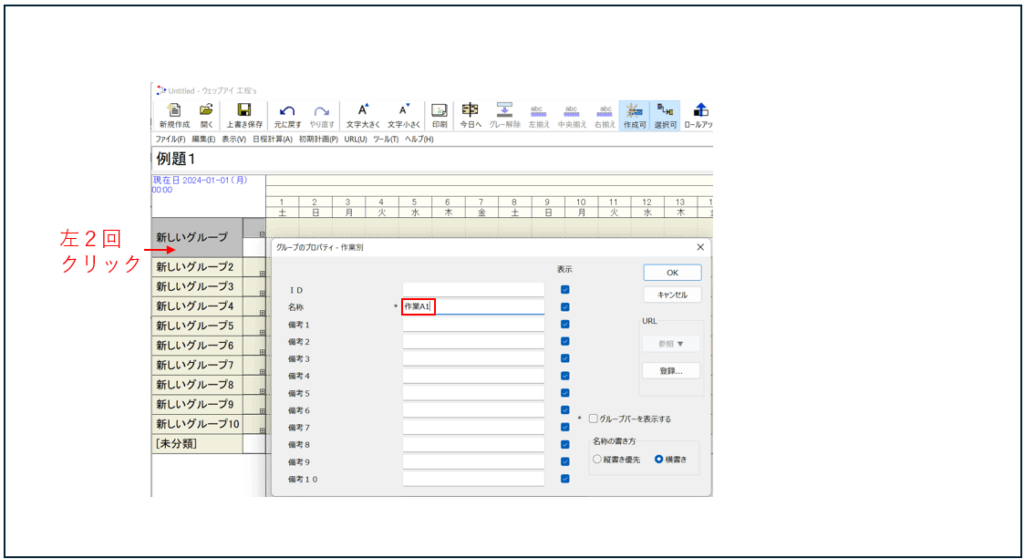
– グループバーの表示・非表示(略)
– ツリービューの表示・非表示
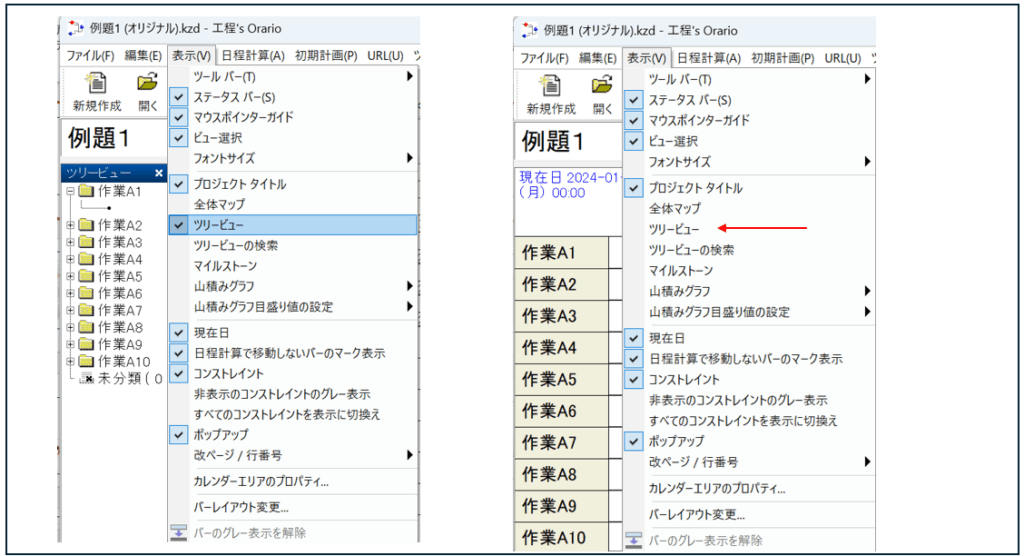
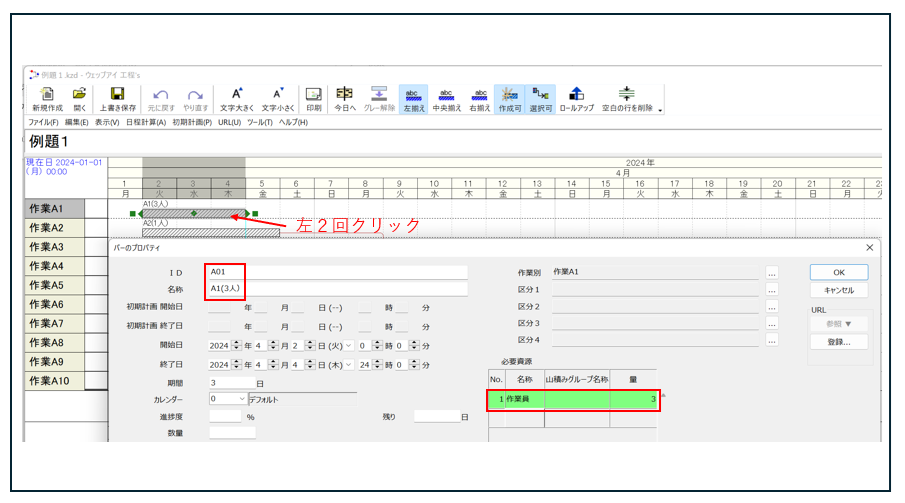
– IDの設定
– 名称の設定
– 必要資源の設定
– シンボル変更(略)
先行制約の定義
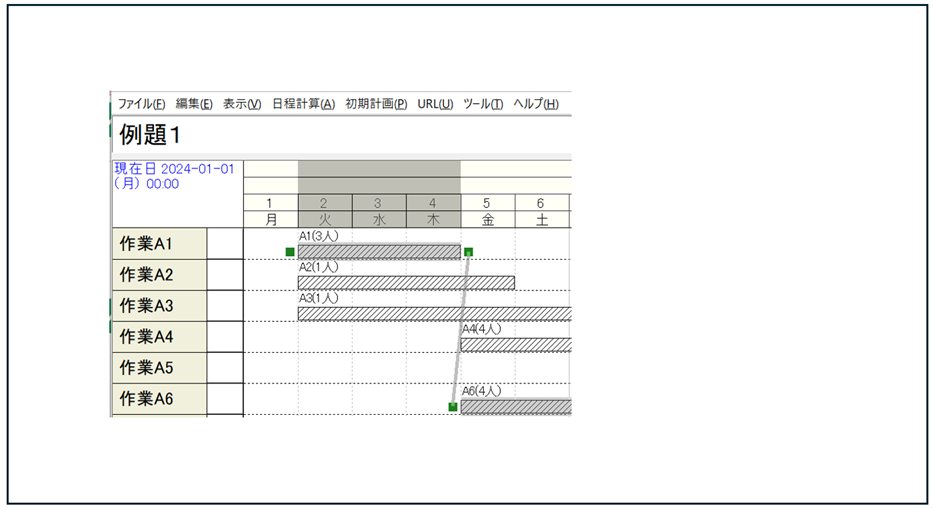 山積み
山積み
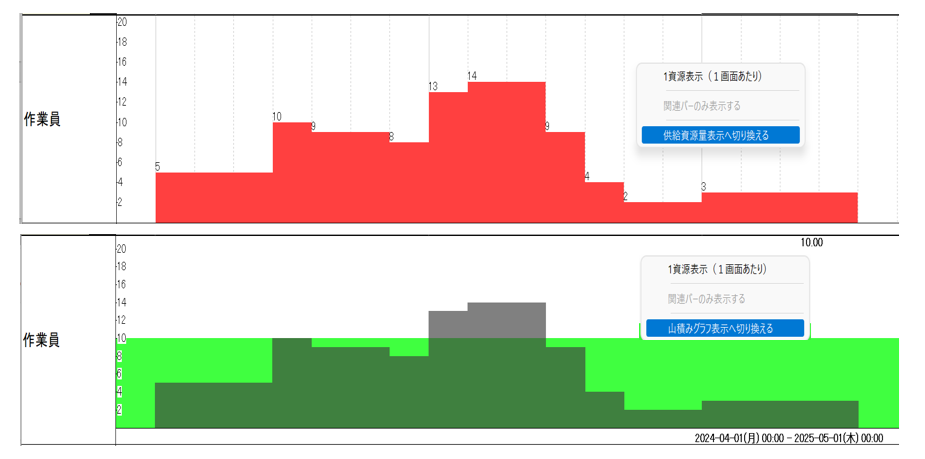
– 供給資源量表示・非表示
– 供給資源量設定補遺1