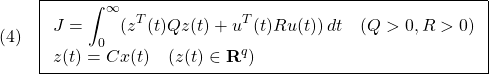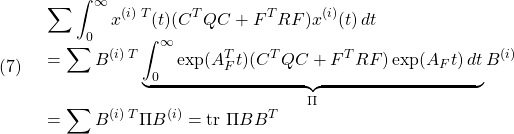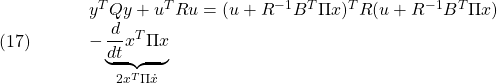2次安定性
[1] 非線形系
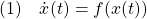
に対してリャプノフ関数
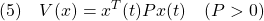
を考えます。これを微分して(1)を用いると((1)の解に沿って微分すると言います)
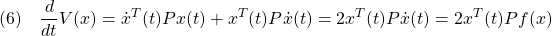
となります。このとき2次安定とは

が成り立つことを言います。これから次式を示すことができ、漸近安定性が成り立ちます。
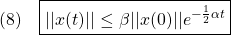
ただし
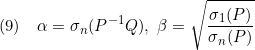
[2] 制御対象が平衡状態にあることは線形状態方程式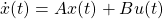 において、
において、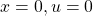 を意味します。そこで平衡状態が乱されて
を意味します。そこで平衡状態が乱されて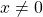 となる時刻を
となる時刻を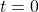 にとると、線形状態方程式は次式となります。
にとると、線形状態方程式は次式となります。
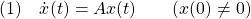
これに出力方程式
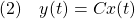
を考慮する場合も含めると、漸近安定性の判定法は次のようにまとめられます。
【漸近安定性の定義とその等価な条件】
定義DA: 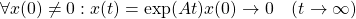
条件A0: 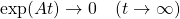
条件A1: 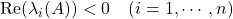
条件A2: 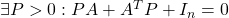
条件A3: 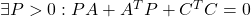 ただし、 ただし、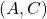 は可観測対 は可観測対
条件A4: 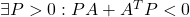
|
まず(1)が漸近安定とすると、条件A2のリャプノフ方程式から次式を得ます。
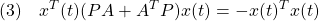
次に(1)に対してリャプノフ関数
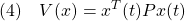
を考えるとき、(3)は2次安定性の条件
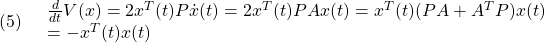
を意味します。これから漸近安定な線形系は2次安定であることが分かります。
●条件A2の両辺から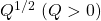 をかけて
をかけて
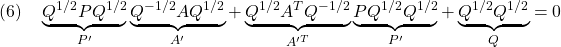
を得ます。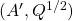 は可観測対なので条件A3を適用して(
は可観測対なので条件A3を適用して( をはずして)
をはずして)
条件A2′: 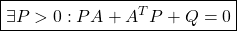 ただし、
ただし、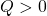
も漸近安定性の条件となることに注意します。
●たとえば、安定行列![Rendered by QuickLaTeX.com \displaystyle{ A= \left[\begin{array}{cc} 0 & 1 \\ -4 & -1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c6c1c66e1cf7b93bac3aad84f54e9744_l3.png)
が与えられるとき、リャプノフ方程式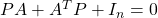 を満足する
を満足する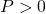 は
は
![Rendered by QuickLaTeX.com \displaystyle{ P=\left[\begin{array}{cc} 2.6250 & 0.1250\\ 0.1250 & 0.6250 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3885fe14c47a46dd2be67bc40c3c8e75_l3.png)
のように求まります。これはMATLABで次のコマンドを用いて計算できます。
ここで、P=lyap(A,Q) はリャプノフ方程式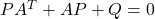 の解を求める関数であることに注意します。
の解を求める関数であることに注意します。
問題設定
[3] 制御対象の状態方程式として次式を考えます。
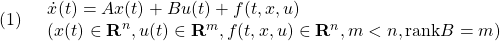
ここで、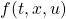 はモデル誤差、非線形要素、外乱などの影響を表し、有界かつ未知とします。これに対し、次のスイッチング関数を定義します。
はモデル誤差、非線形要素、外乱などの影響を表し、有界かつ未知とします。これに対し、次のスイッチング関数を定義します。
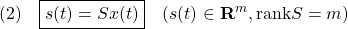
いま(1)の解が、ある時刻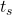 に対して
に対して
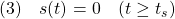
を満足するとき、スライディングモードが発生していると言います。
●以上の準備の下で、スライディングモード制御問題は次のように記述されます。
問題1: 動的システムの振る舞いが閉じ込められる超平面 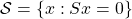 を定義するスイッチング関数を決定せよ。 を定義するスイッチング関数を決定せよ。
問題2: 有限時刻 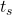 において状態を超平面内に拘束し、引き続き留まらせる( において状態を超平面内に拘束し、引き続き留まらせる(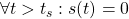 )ことのできるスライディングモード制御則(SM制御則)を設計せよ。 )ことのできるスライディングモード制御則(SM制御則)を設計せよ。 |
●いま、SM制御則を、2次安定性の条件
を、2次安定性
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad %\boxed{ \begin{array}{lll} V(\bar{x})= \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]^T }_{\bar{x}^T(t)} \underbrace{ \left[\begin{array}{cc} P_1 & 0\\ 0 & P_2 \end{array}\right] }_{P} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)}\\ \Rightarrow \dot{V}(\bar{x})\le - \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]^T }_{\bar{x}^T(t)} \underbrace{ \left[\begin{array}{cc} Q_1 & 0\\ 0 & I \end{array}\right] }_{Q} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} \end{array}}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a2747656c1f7d9559f971c1a26fd7023_l3.png)
すなわち
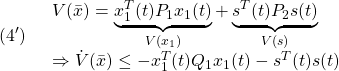
が成り立つように決定します(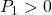 ,
, 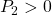 ,
, 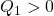 )。
)。
以下で示すように、このSM制御則は次式で表されます。

ここで、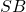 は正則行列であることを仮定しています。また設計パラメータは、スイッチング関数を決める行列
は正則行列であることを仮定しています。また設計パラメータは、スイッチング関数を決める行列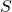 、安定行列
、安定行列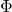 、スカラー
、スカラー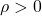 です。
です。
●2重積分器に対して、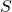 ,
,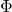 ,
,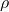 を適当に選んだときのSM制御則の計算は次のように行われます。
を適当に選んだときのSM制御則の計算は次のように行われます。
| MATLAB |
%cDINT_smc.m
%-----
clear all, close all
A=[0 1;
0 0];
B=[0;1];
C=eye(2);
D=zeros(2,1);
M=1;
S=[M 1];
Phi=-1;
P2=lyap(Phi,1);
P2S=P2*S;
Leq=inv(S*B)*S*A;
LPhi=-inv(S*B)*Phi*S;
L=Leq+LPhi;
rho=0.5;
Ln=inv(S*B)*rho;
x0=B;
sim('DINT_smc')
%-----
%eof
|
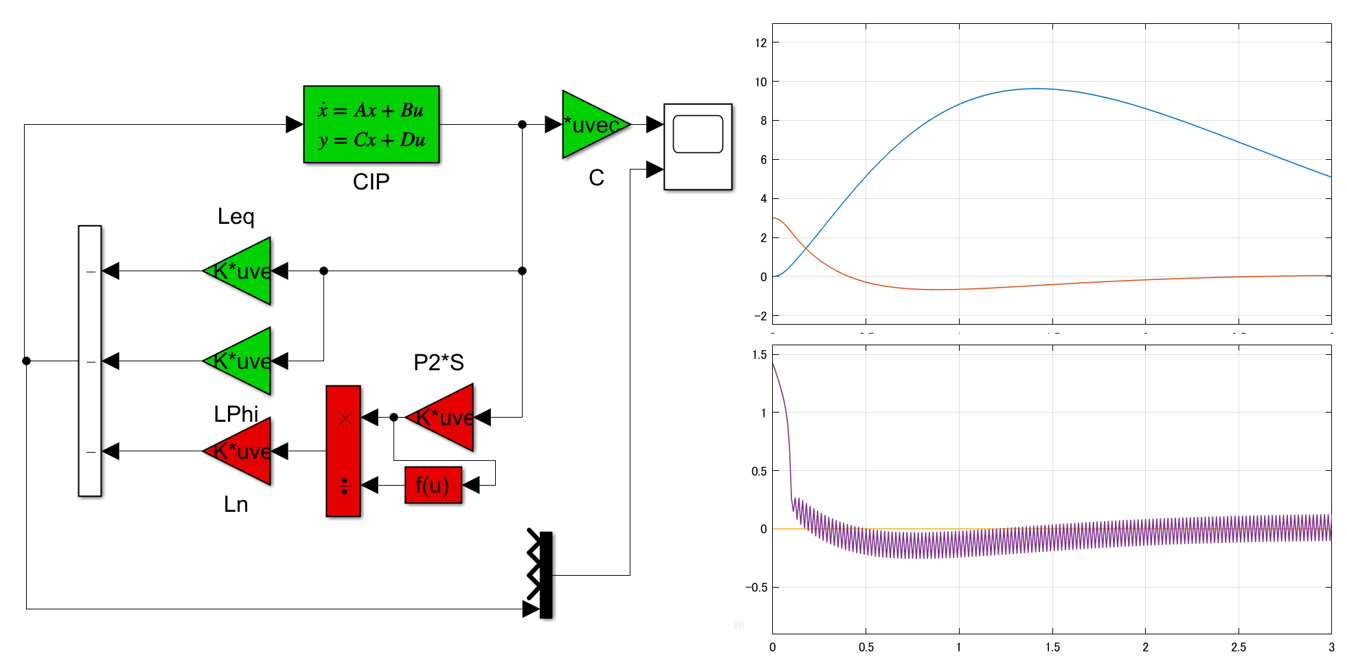
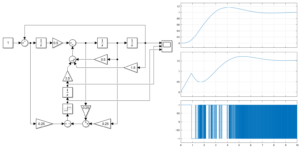
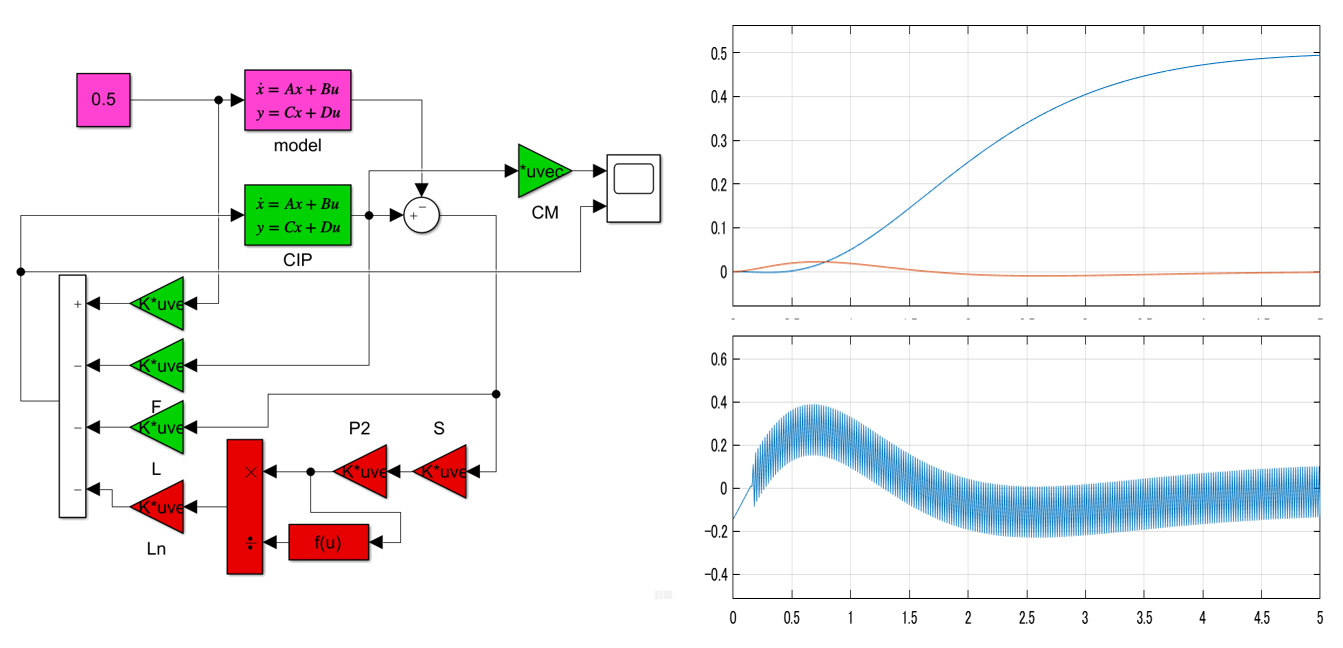
これを実行して、図1aのシミュレーション結果を得ます。

図1a 2重積分器のSM制御
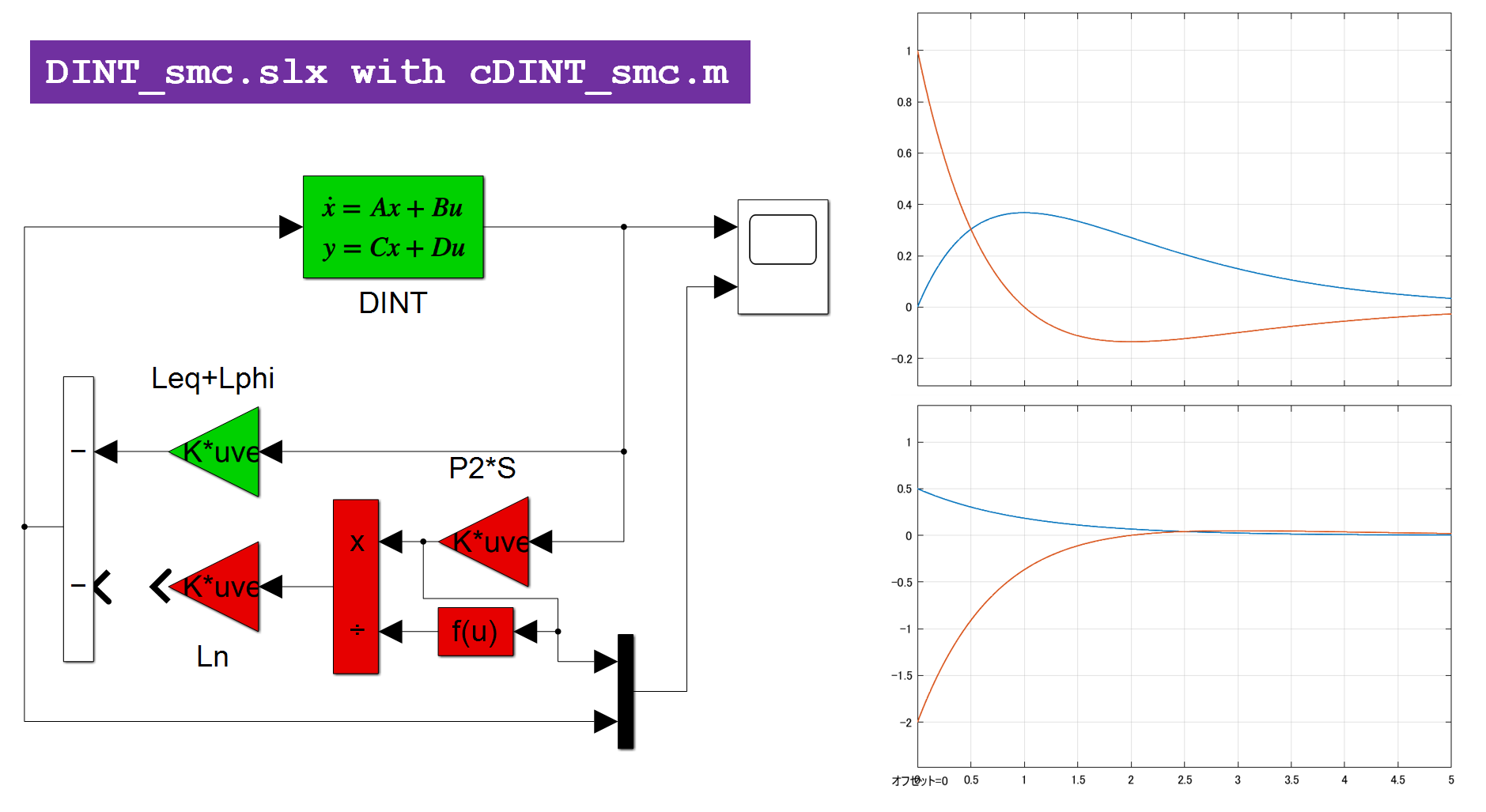
図1b 2重積分器の線形制御(SM制御のスイッチング項を外した場合)
図1bに、SM制御のスイッチング項を外した場合のシミュレーション結果を示します。これらからスイッチング項が速応性の改善に役立っていることが分かります。
●いま(1)において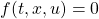 、すなわち
、すなわち
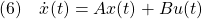
とし、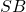 の正則性を仮定します。
の正則性を仮定します。 において、スライディングモード時の制御則は等価制御と呼ばれ、次式のように求められます。
において、スライディングモード時の制御則は等価制御と呼ばれ、次式のように求められます。
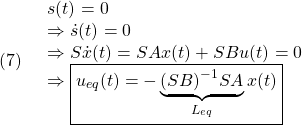
これによる閉ループ系は次式となります。
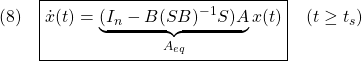
●いま(1)において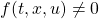 の場合、適合サイズをもつ行列
の場合、適合サイズをもつ行列 を用いて
を用いて
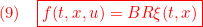
のように表されると仮定します。このとき、等価制御は
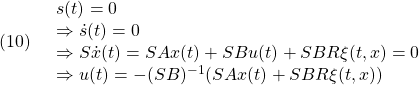
となります。これによる閉ループ系は次式となります。
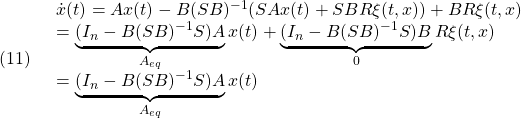
すなわちマッチング条件とよばれる(9)が成り立つとき、スライディングモード時は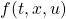 の影響を受けないことが分かります。
の影響を受けないことが分かります。
●剛体振子の運動方程式は次式で与えられました。
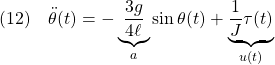
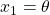 ,
, 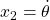 とおいて、次の非線形状態方程式を得ます。
とおいて、次の非線形状態方程式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right]= \left[\begin{array}{cc} x_2(t)\\ -a\sin x_1(t)+u(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-aa83e9dac52ad382b47bbc497cef2e6e_l3.png)
これは、次式のように、2重積分器に非線形項が加えられたものとみなすことができます。
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right]= \left[\begin{array}{cc} 0 & 1\\ 0 & 0 \end{array}\right] \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right]+ \left[\begin{array}{c} 0\\ 1 \end{array}\right] u(t)+ \left[\begin{array}{c} 0\\ -a\sin x_1(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fb895b4100fa03d5604bf0d34248d203_l3.png)
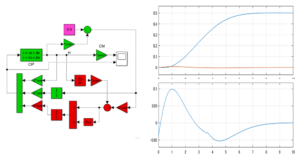
そこで、図1のSM制御則をそのまま用いたときの様子を調べてみます。図2は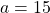 とした場合(
とした場合(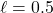 )のシミュレーション結果です。
)のシミュレーション結果です。
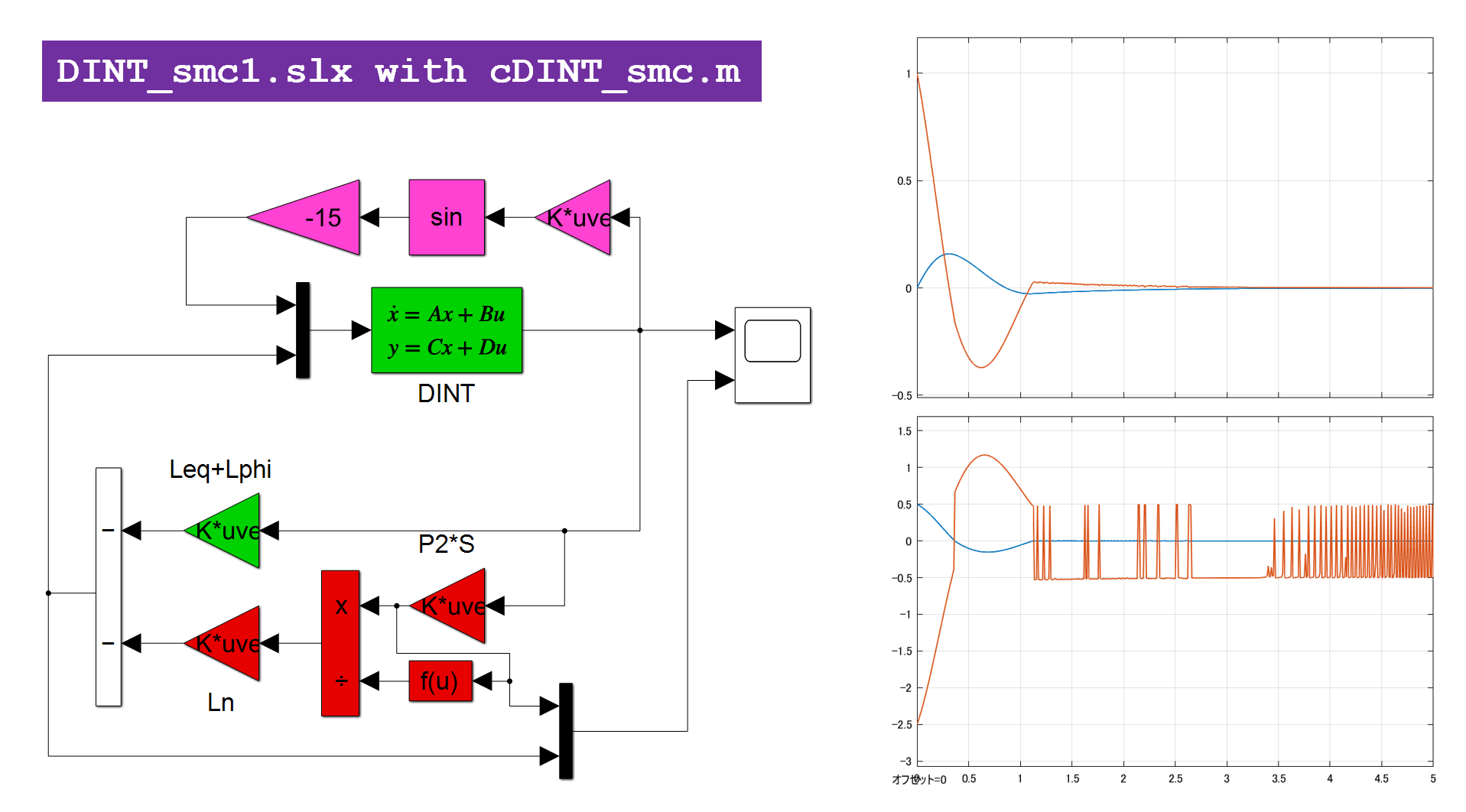
図2a 非線形項を考慮した場合のSM制御
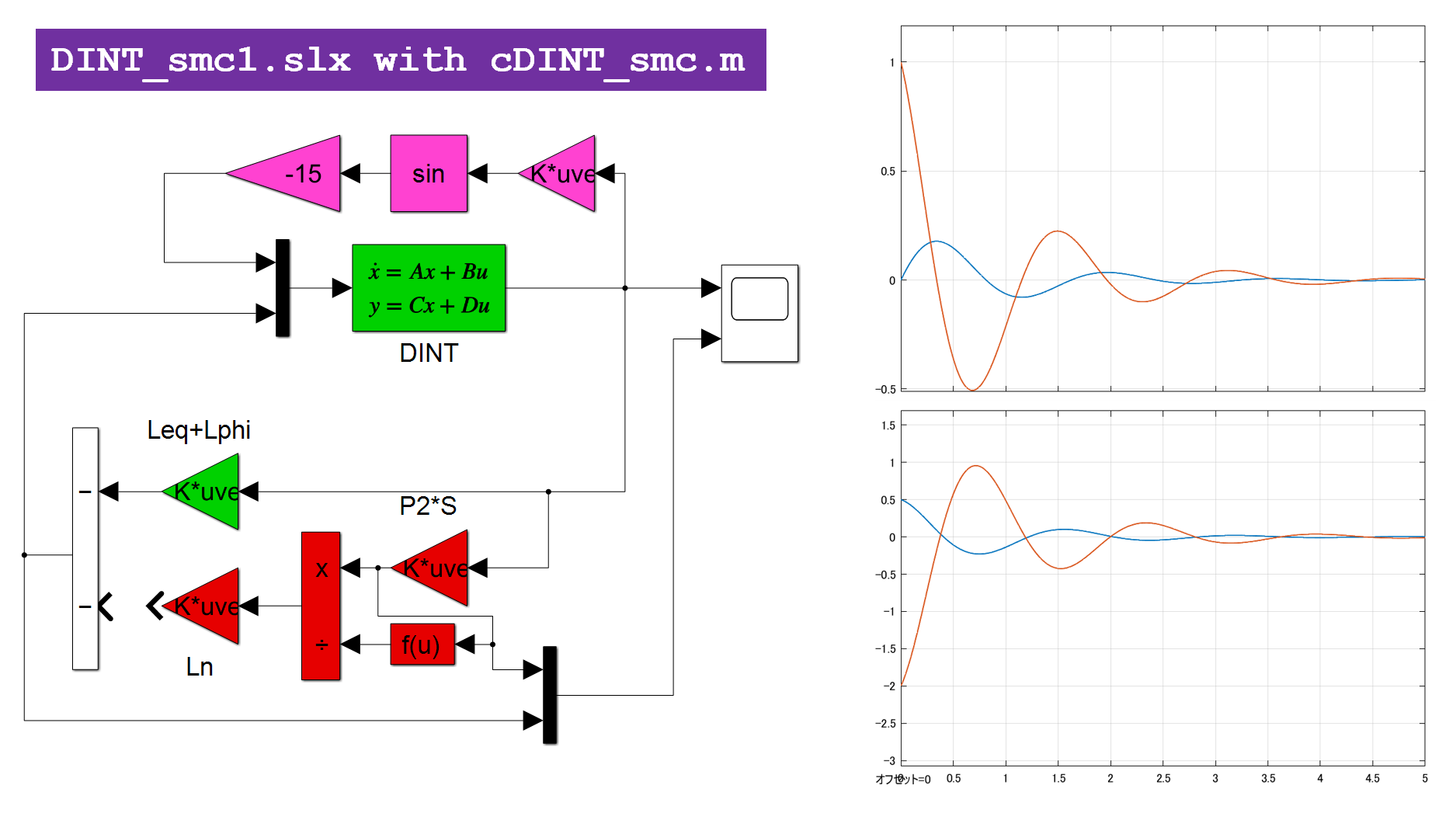
図2b 非線形項を考慮した場合の線形制御(SM制御のスイッチング項を外した場合)
図1のSM制御則は非線形項を考慮していないのですが、マッチング条件が満たされているので、非線形項の影響を抑制していることが分かります。これは図2bのスイッチング項がない場合と比べると明らかです。
SM制御則
[4] 制御対象の状態方程式として次式を考えます。
以下では、状態方程式とスイッチング関数は次のSMC標準形(regular form)をとるように座標変換されていると仮定します(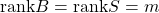 )。
)。
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \boxed{\underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u(t) + \underbrace{ \left[\begin{array}{l} f_u(t,x)\\ f_m(t,x,u) \end{array}\right] }_{f(t,x,u)}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-492c810b2764797d15e8da449fa86719_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \boxed{s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} \ (M=S_2^{-1}S_1)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f362cf2f2a84558f6ce3b7cbfd623471_l3.png)
これに対して、座標変換
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ -S_2^{-1}S_1 & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-aa3c209c1893a28b597ab444a59fa480_l3.png)
を行って、次式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \boxed{ \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{\bar{x}}(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ \bar{A}_{21} & \bar{A}_{22}\\ \end{array}\right] }_{\bar{A}=T_s A T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} + \underbrace{ \left[\begin{array}{c} 0\\ \bar{B}_2 \end{array}\right] }_{\bar{B}=T_sB} u(t)\\ + \underbrace{ \left[\begin{array}{c} f_u(t,x)\\ S_1f_u(t,x)+S_2f_m(t,x,u) \end{array}\right] }_{T_sf(t,x,u)} \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8d94be87e2ee3e86130661d37570a682_l3.png)
ただし
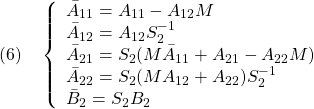
以下では、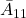 が安定行列となるようにスイッチング関数が選ばれていると仮定します。
が安定行列となるようにスイッチング関数が選ばれていると仮定します。
●SMC標準形に対する等価制御は、 として
として
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{cl} & s(t)=0\ \Rightarrow\ \dot{s}(t)=0\\ \Downarrow & by\ (5)\\ &\bar{A}_{21}x_1(t)+\bar{A}_{22}s(t)+\bar{B}_{2}u(t)=0\\ \Downarrow & \\ (7) & u_{eq}(t)=-\underbrace{\bar{B}_{2}^{-1}}_{([0\ I_m]T_sB)^{-1}} \underbrace{\left[\begin{array}{cc} \bar{A}_{21} & \bar{A}_{22} \\ \end{array}\right]}_{[0\ I_m]T_sAT_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)}\\ \Downarrow & by\ S=[0\ I_m]T_s, x=T_s^{-1}\bar{x}\\ (8) & \boxed{u_{eq}(t)=-\underbrace{(SB)^{-1}SA}_{L_\ell}x(t)}} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2c000a36a1eddd1e979735e5c504c61b_l3.png)
のように得られます。線形制御則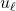 は、この等価制御をベースして
は、この等価制御をベースして
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{cl} (9) & u_{eq}(t)=-\underbrace{\bar{B}_{2}^{-1}}_{([0\ I_m]T_sB)^{-1}} (\underbrace{\left[\begin{array}{cc} \bar{A}_{21} & \bar{A}_{22} \\ \end{array}\right]}_{[0\ I_m]T_sAT_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)}-\Phi s(t))\\ \Downarrow & by\ S=[0\ I_m]T_s, x=T_s^{-1}\bar{x}\\ (10) & \boxed{u_\ell(t)=-\underbrace{(SB)^{-1}(SA-\Phi S)}_{L=L_{eq}+L_{phi}}x(t)}} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f3c7ee69a5490d0416e346e8d6a29a04_l3.png)
のように構成します。ここで、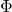 は適当に設定された安定行列です。
は適当に設定された安定行列です。
●このとき閉ループ系は次式で与えられます。
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{s}(t) \end{array}\right] = \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ 0 & \Phi \\ \end{array}\right] \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]\\ + \left[\begin{array}{c} f_u(t,x)\\ \bar{B}_{2}u_n(t)+S_2(Mf_u(t,x)+f_m(t,x,u)) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-08b0fd62ceefdfc7673e603a95165c27_l3.png)
これからスライディングモード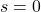 を達成するために
を達成するために の影響を与えることが分かります。簡単な例で確かめると
の影響を与えることが分かります。簡単な例で確かめると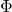 はダンピングを与え、速くスライディングモードを達成するためのパラメータであることが分かります。
はダンピングを与え、速くスライディングモードを達成するためのパラメータであることが分かります。
さて、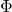 は安定行列なので
は安定行列なので
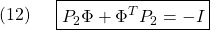
を満たす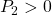 を選ぶことができます。これを用いて、スイッチング制御則
を選ぶことができます。これを用いて、スイッチング制御則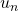 を
を
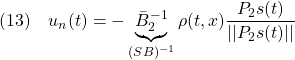
すなわち
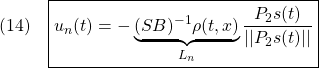
と定めます。線形制御則(10)とスイッチング制御則(14)を用いて、2次安定性を示すことができます。
スイッチング関数(1)
[5] スライディングモードの場合、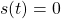 なので
なので
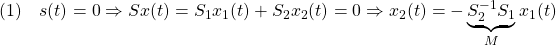
となって、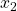 の振る舞いは
の振る舞いは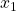 によって決まります。一方、
によって決まります。一方、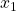 の振る舞いは
の振る舞いは
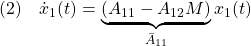
によって決まります。これは
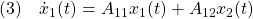
に対する安定化状態フィードバック
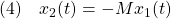
による閉ループ系とみなすことができます。
したがって、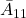 が安定行列となるようにスイッチング関数が選ぶためには、(3)に対する状態フィードバックによる安定化問題を解けばよいことが分かります。
が安定行列となるようにスイッチング関数が選ぶためには、(3)に対する状態フィードバックによる安定化問題を解けばよいことが分かります。
●そこで、次の2次形式評価関数を最小にするように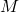 を決定する方法が提案されています。
を決定する方法が提案されています。
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \boxed{J=\int_0^\infty \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right]^T }_{x^T(t)} \underbrace{ \left[\begin{array}{cc} Q_{11} & Q_{12} \\ Q_{21} & Q_{22} \end{array}\right] }_{Q} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} dt} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-13ff85a64857f296223fc5fc4db3a6fc_l3.png)
これは
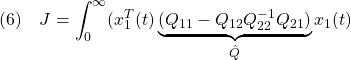
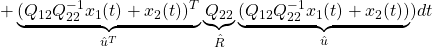
と書けます。ここで、(3)と(4)をそれぞれ
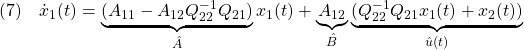
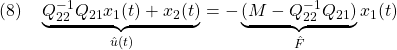
と書き直すと、次のような最適化制御問題の定式化ができていることがわかります。すなわち
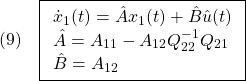
を2次系式評価関数
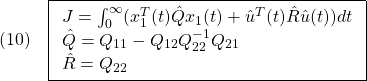
を最小にするように
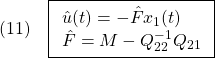
を求める問題です。この解は、リッカチ方程式
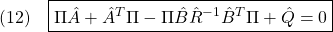
を解いて
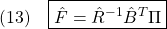
を求め、次式から を決めればよいことがわかります。
を決めればよいことがわかります。
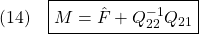
●2重積分器に対して、関数swflqrによるスイッチング関数Sの決定は次のように行われます。
| MATLAB |
%cDINT_smc1.m
%-----
clear all, close all
A=[0 1;
0 0];
B=[0;1];
C=eye(2);
D=zeros(2,1);
Mx=0.5; Tx=0.5;
Q=diag([1/Mx,Tx/Mx].^2);
S=swflqr(A,B,Q)
Phi=-1;
P2=lyap(Phi,1);
P2S=P2*S;
Leq=inv(S*B)*S*A;
LPhi=-inv(S*B)*Phi*S;
L=Leq+LPhi;
rho=0.5;
Ln=inv(S*B)*rho;
x0=B;
sim('DINT_smc')
%-----
%eof
|
これを実行して図3のシミュレーション結果を得ます。
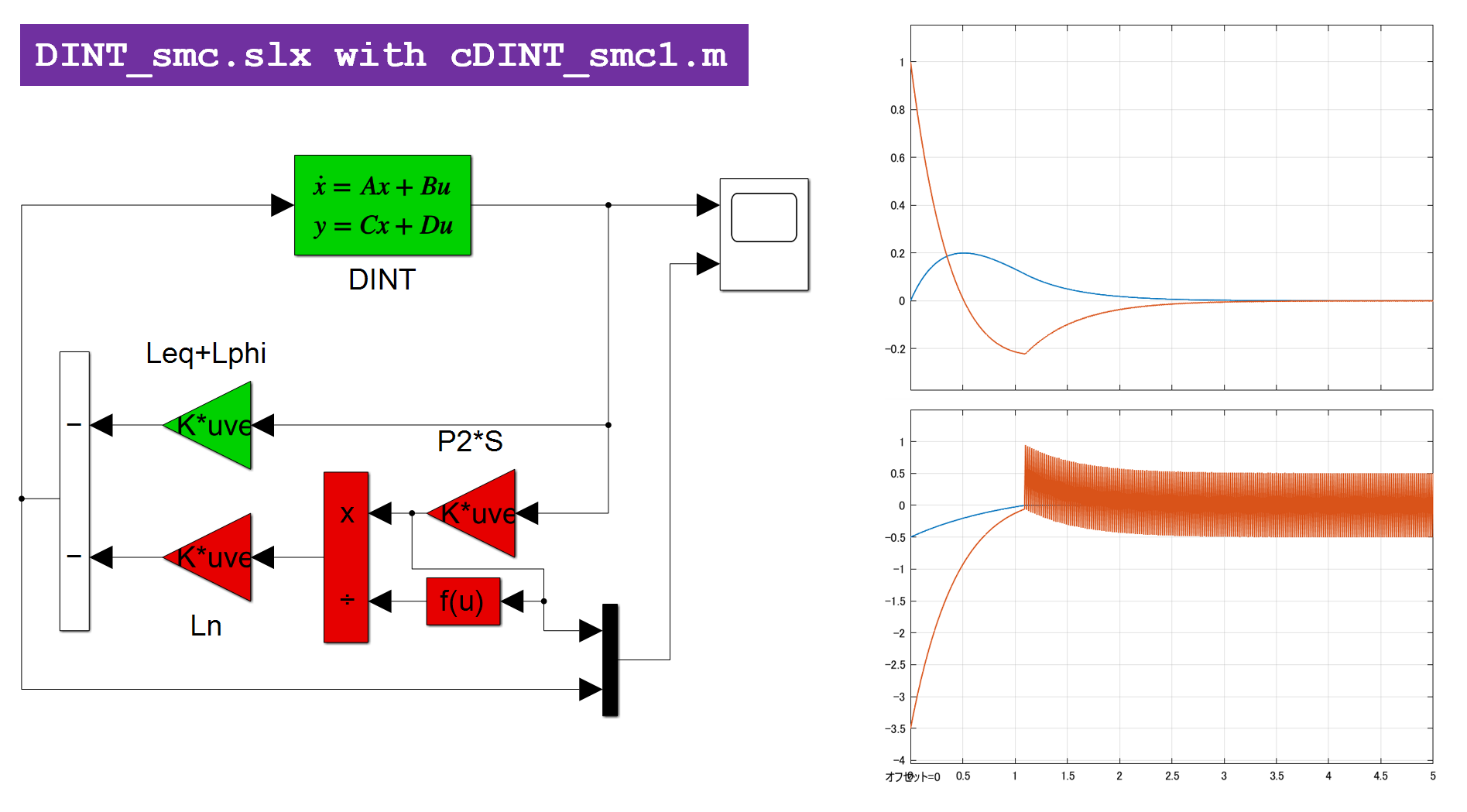
図3 関数swflqrによるスイッチング関数Sの決定
ここで、関数swflqrは、Edwards and Spurgeon によるものです。
スイッチング関数(2)
[6] 等価制御
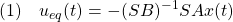
による閉ループ系は次式で表されました。
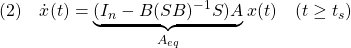
ここで
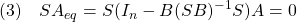
また、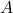 、
、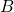 、
、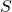 は、SMC標準形で与えられるとすると
は、SMC標準形で与えられるとすると
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} A_{eq}= \underbrace{ \left[\begin{array}{cc} I & 0 \\ -M & 0 \\ \end{array}\right] }_{I_n-B(SB)^{-1}S} \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right]= \left[\begin{array}{cc} A_{11} & A_{12} \\ -MA_{11} & -MA_{12} \\ \end{array}\right]\\ = \left[\begin{array}{cc} I & 0 \\ -M & I \\ \end{array}\right] \left[\begin{array}{cc} \bar{A}_{11} & A_{12} \\ 0 & 0 \\ \end{array}\right] \left[\begin{array}{cc} I & 0 \\ -M & I \\ \end{array}\right]^{-1} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2474825aa676243c02182b9e5a87f0f1_l3.png)
となって、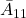 が安定行列なので、
が安定行列なので、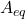 は
は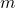 個の零固有値を持ちます。一方、
個の零固有値を持ちます。一方、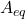 の非零固有値
の非零固有値 に対応する固有ベクトルを
に対応する固有ベクトルを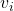 とすると、
とすると、
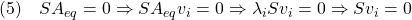
すなわち
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad { \boxed{S[v_1\cdots v_{n-m}]=0 % \Rightarrow [v_1\cdots v_{n-m}]^TS^T=0}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-33964edd7a6349891872237b63b937ec_l3.png)
が成り立ちます。したがって、まず等価制御による閉ループ系の が望ましい固有値・固有ベクトルをもつように設計して、(5)から
が望ましい固有値・固有ベクトルをもつように設計して、(5)から を決定することが考えられます。
を決定することが考えられます。
●2重積分器に対して、関数swfvplによるスイッチング関数Sの決定は次のように行われます。
| MATLAB |
%cDINT_smc2.m
%-----
clear all, close all
A=[0 1;
0 0];
B=[0;1];
C=eye(2);
D=zeros(2,1);
lambda=-1;
nocomp=0;
specpos=rand(2,1)
specent=rand(2,1)
S=swfvpl(A,B,lambda,nocomp,specpos,specent)
Phi=-1;
P2=lyap(Phi,1);
P2S=P2*S;
Leq=inv(S*B)*S*A;
LPhi=-inv(S*B)*Phi*S;
L=Leq+LPhi;
rho=0.5;
Ln=inv(S*B)*rho;
x0=B;
sim('DINT_smc')
%-----
%eof
|
これを実行して図4のシミュレーション結果を得ます。
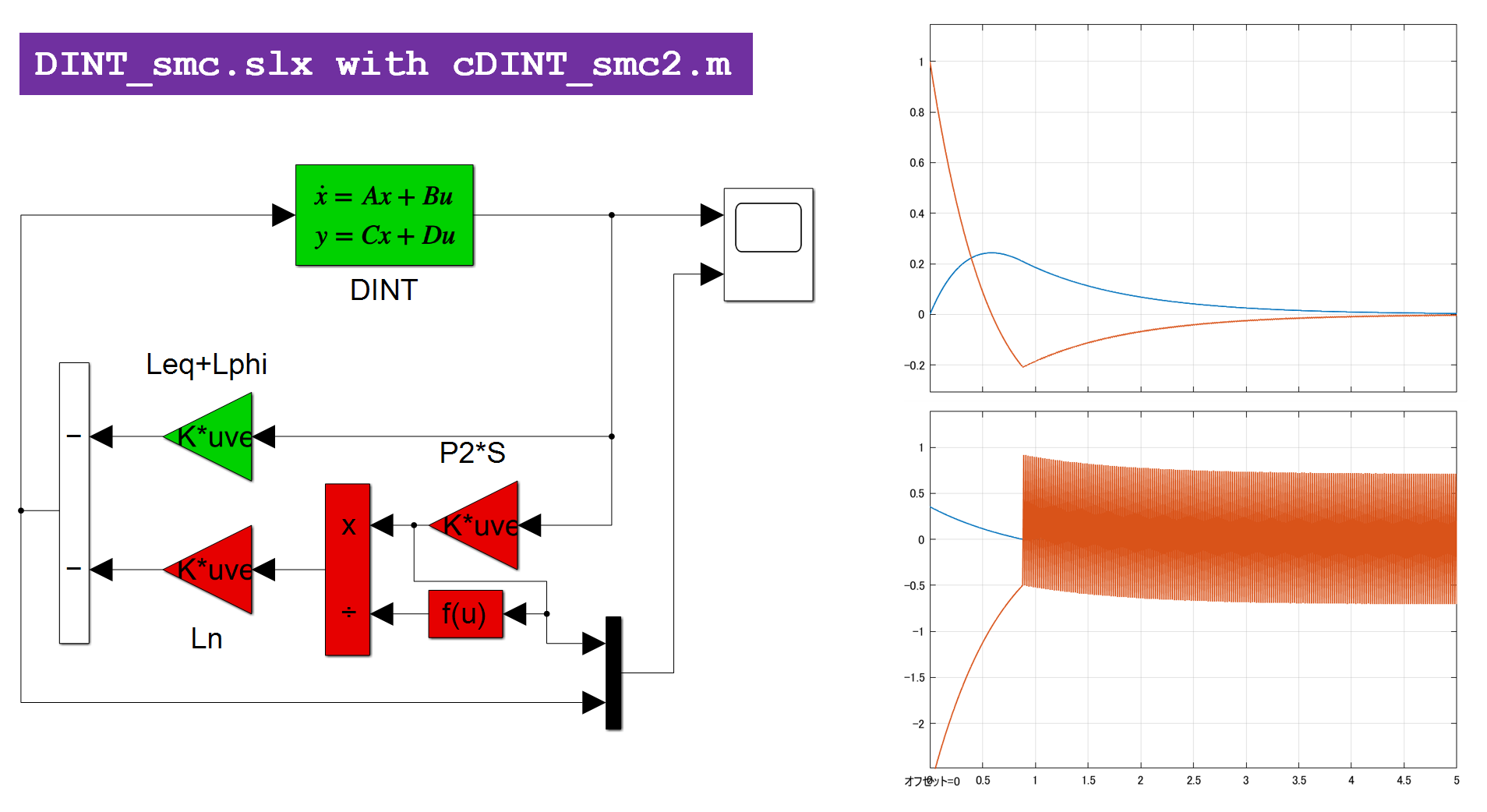
図4 関数swfvplによるスイッチング関数Sの決定
ここで、関数swfvplは、Edwards and Spurgeon によるものです。
積分動作の導入
[6] 定値外乱を受ける制御対象
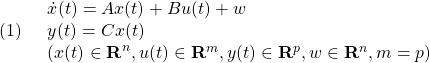
の出力を、次のコマンド(定値目標)
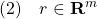
に追従させることを考えます。そのために、積分動作
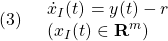
を考え、次の拡大系を構成します。
偏差系E3:
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{\dot{x}_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} \underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3c19e131ef7f7e62fb75b0b722359667_l3.png)
を得ます。この偏差系E3が標準形となっていることに注意して、SMCを設計します。
(4)を、改めて次のように書きます。
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot{x}_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} + \underbrace{ \left[\begin{array}{c} 0\\ I_m \end{array}\right] }_{B_{E3}} {\dot u}(t)\\ (x_1(t)=x(t)-x_\infty, x_2(t)=u(t)-u_\infty) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3651de7cb254ab2cb45e5409ae9cd171_l3.png)
スイッチング関数として、次式を考えます。
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} \ (M=S_2^{-1}S_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-841f3fca38a28aec9d1c570b17f6f7ec_l3.png)
(15)に対して、座標変換
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ -S_2^{-1}S_1 & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-94c9c19111e524fb6b7adf025beef334_l3.png)
を行って、次式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{x}'_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ \bar{A}_{21} & \bar{A}_{22} \\ \end{array}\right] }_{T_sA_{E3}T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} + \underbrace{ \left[\begin{array}{cc} 0\\ S_2 \end{array}\right] }_{T_sB_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-922fcb090845e1f769269f768e72eda3_l3.png)
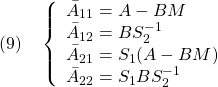
以下では、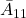 が安定行列となるようにスイッチング関数が選ばれていると仮定します。
が安定行列となるようにスイッチング関数が選ばれていると仮定します。
このとき、SM制御則を、2次安定性
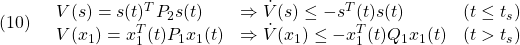
が成り立つように決定します(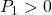 ,
, 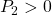 ,
, 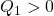 )。
)。
偏差系E3に対するSMCは次式で与えられます。
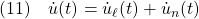
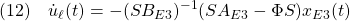
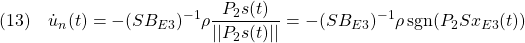
これらを積分して、制御対象(1)に対する積分動作をもつSMCを導出します。
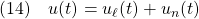
まず(12)は次式のように書けます。
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad {\dot u}_\ell(t)=- \boxed{\underbrace{ (SB_{E3})^{-1}(SA_{E3}-\Phi S)S_E^{-1} }_{\left[\begin{array}{cc} F & F_I \end{array}\right]}} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-09bdbdbd69d8bc1d816020ba9b4ba6d8_l3.png)
これを積分して
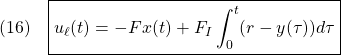
次に(13)は次式のように書けます。
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad {\dot u}_n(t) =-(SB_{E3})^{-1}\rho\, {\rm sgn}( \boxed{\underbrace{ P_2SS_E^{-1} }_{\left[\begin{array}{cc} G & G_I \end{array}\right]}} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)}) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-88922723347229f2a9ac74335912e98d_l3.png)
これを積分すれば
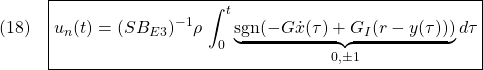
●2重積分器に対して、次のように行われます。
| MATLAB |
%cDINT_smci.m
%-----
clear all, close all
A=[0 1;
0 0];
B=[0;1];
C=[1 0];
D=0;
n=size(A,1); m=size(B,2); p=size(C,1);
AE=[A B;zeros(m,n+m)];
BE=[zeros(n,m);eye(m)];
SE=[A B;C D];
QE=eye(n+m);
S=-swflqr(AE,BE,QE)
Phi=-0.5;
Leq=inv(S*BE)*S*AE;
LPhi=-inv(S*BE)*Phi*S;
L=(Leq+LPhi)/SE;
F=L(1:2)
FI=L(3)
P2=lyap(Phi,1)
P2S=P2*S/SE;
G=P2S(1:2)
GI=P2S(3)
rho=1;
Ln=inv(S*BE)*rho
x0=zeros(2,1);
sim('DINT_smci')
%-----
%eof
|
これを実行して図5のシミュレーション結果を得ます。
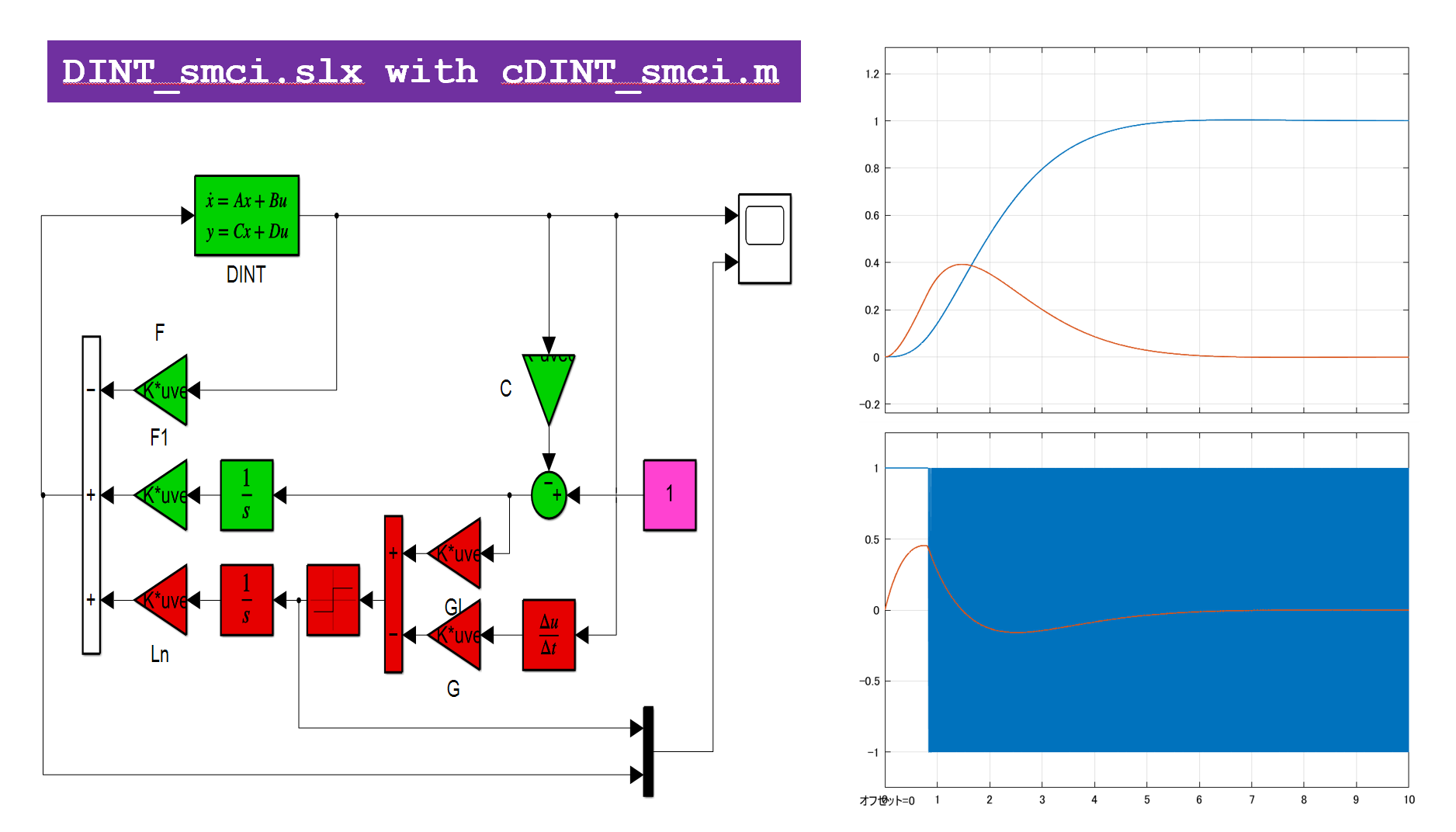
図5 積分動作を導入したSM制御
補遺:2次安定系のロバスト性…Homework
いま漸近安定な線形系
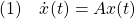
において次のようなモデルの不確かさがあるとします。
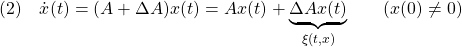
条件A2’より、適当な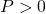 と
と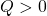 に対して
に対して
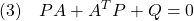
が成り立ちます。このとき
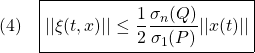
ならば、リャプノフ関数
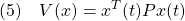
に対して
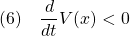
となって、リャプノフ安定となります。
●実際、
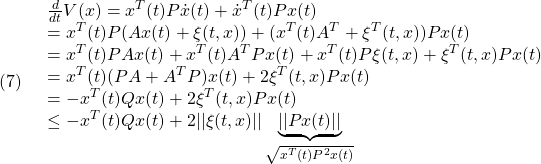
ここで、
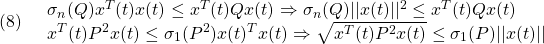
に注意して、(4)の下では
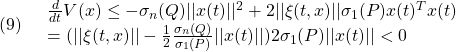
となります。
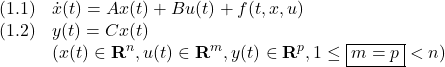
![]() はモデル誤差、非線形要素、外乱などの影響を表し、次のマッチング条件を満たすとします。
はモデル誤差、非線形要素、外乱などの影響を表し、次のマッチング条件を満たすとします。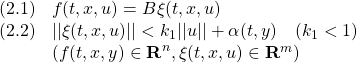
![]()
![Rendered by QuickLaTeX.com \displaystyle{(4.1)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} \underbrace{(u(t)+\xi(t,x,u))}_{u'(t)}\\ (x_1(t)\in{\rm\bf R}^{n-m}, x_2(t)\in{\rm\bf R}^m, B_2\in{\rm\bf R}^{m\times m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9d9eabcd36c3ce62bf09a0d32ce9ea07_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4.2)\quad y(t)= \underbrace{ \left[\begin{array}{cc} C_{1} & C_{2} \\ \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)}\quad (y(t)\in{\rm\bf R}^m, C_2\in{\rm\bf R}^{m\times m}) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6b6bf798fce1fca1e7b12540a2a4e9a3_l3.png)
![]() は(4.1)と(4.2)のような分割をもつとします。
は(4.1)と(4.2)のような分割をもつとします。![Rendered by QuickLaTeX.com \displaystyle{(5)\quad s(t)=Fy(t)=F \underbrace{ \left[\begin{array}{cc} C_{1} & C_{2} \\ \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} =\underbrace{ \left[\begin{array}{cc} FC_{1} & FC_{2} \\ \end{array}\right] }_{S=FC} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a3e37089e535379edc227db046808e5a_l3.png)
![]() は
は![]()
![]() を仮定します。このとき、正方行列
を仮定します。このとき、正方行列![]() はすべて正則となります。
はすべて正則となります。![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{\bar{x}(t)} = \underbrace{ \left[\begin{array}{cc} I_{n-m}& 0 \\ C_1 & C_2 \\ \end{array}\right] }_{T_y} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} = \underbrace{ \left[\begin{array}{cc} I_{n-m}& 0 \\ -C_2^{-1}C_1 & C_2^{-1} \end{array}\right] }_{T_y^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{\bar{x}(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-36294dfd18793309878ccd0d8385bbb5_l3.png)
![]() )
)![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc} I_{n-m} & 0 \\ -M & C_2^{-1} \\ \end{array}\right] }_{T_y^{-1}} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot y(t) \end{array}\right] }_{\dot{\bar{x}}(t)}\\ = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{cc} I_{n-m} & 0 \\ -M & C_2^{-1} \\ \end{array}\right] }_{T_y^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{\bar{x}(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u'(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-09b99785d09eb2ea3c9cda05273c87f9_l3.png)
![]() をかけて
をかけて![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot y(t) \end{array}\right] }_{\dot{\bar{x}}(t)} = \underbrace{ \left[\begin{array}{cc} I_{n-m} & 0 \\ C_1 & C_2 \\ \end{array}\right] }_{T_y} \underbrace{ \left[\begin{array}{cc} A_{11}-A_{12}M & A_{12}C_2^{-1} \\ A_{21}-A_{22}M & A_{22}C_2^{-1} \\ \end{array}\right] }_{AT_y^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{\bar{x}(t)}\\ + \underbrace{ \left[\begin{array}{cc} I_{n-m} & 0 \\ C_1 & C_2 \\ \end{array}\right] }_{T_y} \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u'(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-576672e3c0ab015015806803be5be6e0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \boxed{ %\begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot y(t) \end{array}\right] }_{\dot{\bar{x}}(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ \bar{A}_{21} & \bar{A}_{22}\\ \end{array}\right] }_{\bar{A}=T_y A T_y^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{\bar{x}(t)} + \underbrace{ \left[\begin{array}{c} 0\\ \bar{B}_2 \end{array}\right] }_{\bar{B}=T_yB} u'(t) %\end{array} }}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-551b974cb60f73d29035528b00414fb6_l3.png)
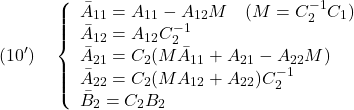
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \boxed{y(t)= \underbrace{ \left[\begin{array}{cc} 0 & I_{m} \\ \end{array}\right] }_{\bar{C}=CT_y^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{\bar{x}(t)}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6d572a784a0d5d01341f3c1a7bf72075_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \boxed{s(t)=Fy(t)= \underbrace{ \left[\begin{array}{cc} 0 & F \\ \end{array}\right] }_{F\bar{C}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{\bar{x}(t)}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5b3fac9c95c90b06d76da8172b3c27ba_l3.png)
![]() の固有値が
の固有値が ![]() の不変零点に等しく、スライディングモードの振舞いを決めます。しかし、
の不変零点に等しく、スライディングモードの振舞いを決めます。しかし、![]() ですから、
ですから、![]() には選択の自由度がないことに注意します。
には選択の自由度がないことに注意します。![]() 、
、![]() 、
、![]() 、
、![]() のバーをとって記述します。
のバーをとって記述します。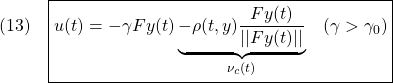
![]() と
と![]() は設計パラメータ、
は設計パラメータ、![]() は後で示す定数です。
は後で示す定数です。![]()
![]()
![]() ,
, ![]() )。ただし、次式を仮定します。
)。ただし、次式を仮定します。![]()
![]()
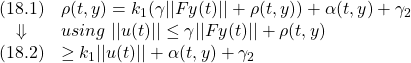
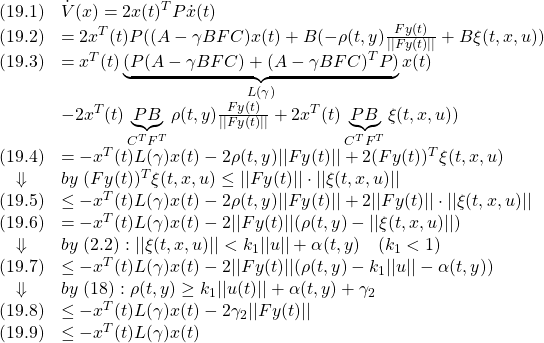
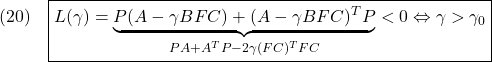
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{cl} (21.1) & L(\gamma)=PA+A^TP-2\gamma (FC)^TFC\\ (21.2) & =\underbrace{\left[ \begin{array}{cc} P_1 & 0 \\ 0 & P_2 \\ \end{array}\right]}_{P} \underbrace{\left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right]}_{A} + \underbrace{\left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right]^T}_{A^T} \underbrace{\left[\begin{array}{cc} P_1 & 0 \\ 0 & P_2 \\ \end{array}\right]}_{P}\\ &-2\gamma \underbrace{\left[\begin{array}{cc} 0 & F \\ \end{array}\right]^T}_{(FC)^T} \underbrace{\left[\begin{array}{cc} 0 & F \\ \end{array}\right]}_{FC}\\ (21.3) & =\left[ \begin{array}{cc} P_1A_{11}+A_{11}^TP_1 & P_1A_{12}+A_{21}^TP_2 \\ (P_1A_{12}+A_{21}^TP_2)^T & P_2A_{22}+A_{22}^TP_2 \\ \end{array}\right] -2\gamma \left[\begin{array}{cc} 0 & 0 \\ 0 & F^TF \\ \end{array}\right]\\ (21.4) & =\left[\begin{array}{cc} P_1A_{11}+A_{11}^TP_1 & P_1A_{12}+A_{21}^TP_2 \\ (P_1A_{12}+A_{21}^TP_2)^T & P_2A_{22}+A_{22}^TP_2-2\gamma F^TF \\ \end{array}\right]<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d90e2269d72fb880ea00c58c13b87908_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(22)\quad \begin{array}{l} \left[\begin{array}{cc} X & Z \\ Z^T & Y \end{array}\right]<0\\ \ \Leftrightarrow\ X-ZY^{-1}Z^T<0,\ Y<0 \\ \ \Leftrightarrow\ X<0,\ Y-Z^TX^{-1}Z<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5ad5723e74a49a0f86149626e8834da7_l3.png)
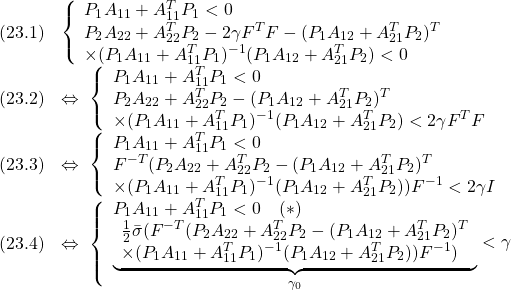
![]() が
が![]() となるための条件となることが分かります。
となるための条件となることが分かります。
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad %\boxed{ \begin{array}{lll} V(\bar{x})= \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]^T }_{\bar{x}^T(t)} \underbrace{ \left[\begin{array}{cc} P_1 & 0\\ 0 & P_2 \end{array}\right] }_{P} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)}\\ \Rightarrow \dot{V}(\bar{x})\le - \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]^T }_{\bar{x}^T(t)} \underbrace{ \left[\begin{array}{cc} Q_1 & 0\\ 0 & I \end{array}\right] }_{Q} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} \end{array}}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a2747656c1f7d9559f971c1a26fd7023_l3.png)
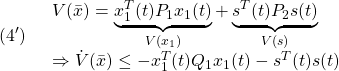



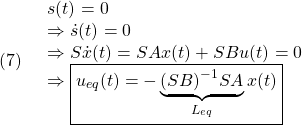
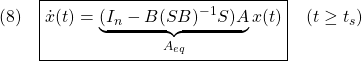
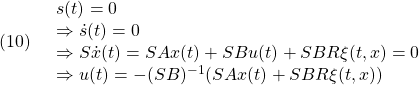
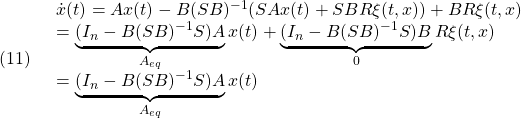
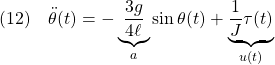


![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \boxed{\underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u(t) + \underbrace{ \left[\begin{array}{l} f_u(t,x)\\ f_m(t,x,u) \end{array}\right] }_{f(t,x,u)}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-492c810b2764797d15e8da449fa86719_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \boxed{s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} \ (M=S_2^{-1}S_1)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f362cf2f2a84558f6ce3b7cbfd623471_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ -S_2^{-1}S_1 & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-aa3c209c1893a28b597ab444a59fa480_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \boxed{ \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{\bar{x}}(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ \bar{A}_{21} & \bar{A}_{22}\\ \end{array}\right] }_{\bar{A}=T_s A T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} + \underbrace{ \left[\begin{array}{c} 0\\ \bar{B}_2 \end{array}\right] }_{\bar{B}=T_sB} u(t)\\ + \underbrace{ \left[\begin{array}{c} f_u(t,x)\\ S_1f_u(t,x)+S_2f_m(t,x,u) \end{array}\right] }_{T_sf(t,x,u)} \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8d94be87e2ee3e86130661d37570a682_l3.png)
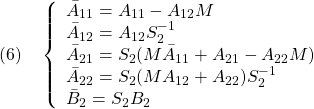
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{cl} & s(t)=0\ \Rightarrow\ \dot{s}(t)=0\\ \Downarrow & by\ (5)\\ &\bar{A}_{21}x_1(t)+\bar{A}_{22}s(t)+\bar{B}_{2}u(t)=0\\ \Downarrow & \\ (7) & u_{eq}(t)=-\underbrace{\bar{B}_{2}^{-1}}_{([0\ I_m]T_sB)^{-1}} \underbrace{\left[\begin{array}{cc} \bar{A}_{21} & \bar{A}_{22} \\ \end{array}\right]}_{[0\ I_m]T_sAT_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)}\\ \Downarrow & by\ S=[0\ I_m]T_s, x=T_s^{-1}\bar{x}\\ (8) & \boxed{u_{eq}(t)=-\underbrace{(SB)^{-1}SA}_{L_\ell}x(t)}} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2c000a36a1eddd1e979735e5c504c61b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{cl} (9) & u_{eq}(t)=-\underbrace{\bar{B}_{2}^{-1}}_{([0\ I_m]T_sB)^{-1}} (\underbrace{\left[\begin{array}{cc} \bar{A}_{21} & \bar{A}_{22} \\ \end{array}\right]}_{[0\ I_m]T_sAT_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)}-\Phi s(t))\\ \Downarrow & by\ S=[0\ I_m]T_s, x=T_s^{-1}\bar{x}\\ (10) & \boxed{u_\ell(t)=-\underbrace{(SB)^{-1}(SA-\Phi S)}_{L=L_{eq}+L_{phi}}x(t)}} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f3c7ee69a5490d0416e346e8d6a29a04_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{s}(t) \end{array}\right] = \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ 0 & \Phi \\ \end{array}\right] \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]\\ + \left[\begin{array}{c} f_u(t,x)\\ \bar{B}_{2}u_n(t)+S_2(Mf_u(t,x)+f_m(t,x,u)) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-08b0fd62ceefdfc7673e603a95165c27_l3.png)
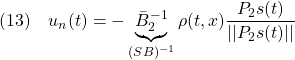
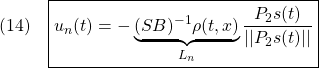
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \boxed{J=\int_0^\infty \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right]^T }_{x^T(t)} \underbrace{ \left[\begin{array}{cc} Q_{11} & Q_{12} \\ Q_{21} & Q_{22} \end{array}\right] }_{Q} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} dt} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-13ff85a64857f296223fc5fc4db3a6fc_l3.png)
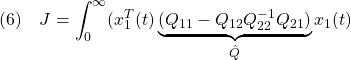
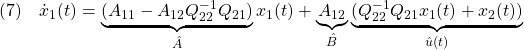
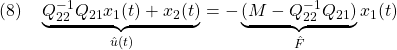
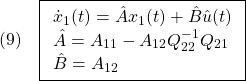
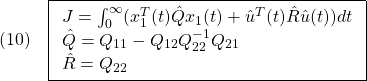
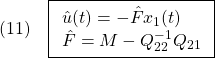

![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} A_{eq}= \underbrace{ \left[\begin{array}{cc} I & 0 \\ -M & 0 \\ \end{array}\right] }_{I_n-B(SB)^{-1}S} \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right]= \left[\begin{array}{cc} A_{11} & A_{12} \\ -MA_{11} & -MA_{12} \\ \end{array}\right]\\ = \left[\begin{array}{cc} I & 0 \\ -M & I \\ \end{array}\right] \left[\begin{array}{cc} \bar{A}_{11} & A_{12} \\ 0 & 0 \\ \end{array}\right] \left[\begin{array}{cc} I & 0 \\ -M & I \\ \end{array}\right]^{-1} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2474825aa676243c02182b9e5a87f0f1_l3.png)

![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{\dot{x}_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} \underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3c19e131ef7f7e62fb75b0b722359667_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot{x}_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} + \underbrace{ \left[\begin{array}{c} 0\\ I_m \end{array}\right] }_{B_{E3}} {\dot u}(t)\\ (x_1(t)=x(t)-x_\infty, x_2(t)=u(t)-u_\infty) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3651de7cb254ab2cb45e5409ae9cd171_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} \ (M=S_2^{-1}S_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-841f3fca38a28aec9d1c570b17f6f7ec_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ -S_2^{-1}S_1 & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-94c9c19111e524fb6b7adf025beef334_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{x}'_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ \bar{A}_{21} & \bar{A}_{22} \\ \end{array}\right] }_{T_sA_{E3}T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} + \underbrace{ \left[\begin{array}{cc} 0\\ S_2 \end{array}\right] }_{T_sB_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-922fcb090845e1f769269f768e72eda3_l3.png)
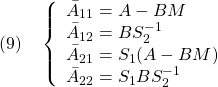
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad {\dot u}_\ell(t)=- \boxed{\underbrace{ (SB_{E3})^{-1}(SA_{E3}-\Phi S)S_E^{-1} }_{\left[\begin{array}{cc} F & F_I \end{array}\right]}} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-09bdbdbd69d8bc1d816020ba9b4ba6d8_l3.png)
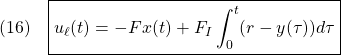
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad {\dot u}_n(t) =-(SB_{E3})^{-1}\rho\, {\rm sgn}( \boxed{\underbrace{ P_2SS_E^{-1} }_{\left[\begin{array}{cc} G & G_I \end{array}\right]}} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)}) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-88922723347229f2a9ac74335912e98d_l3.png)
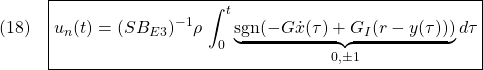

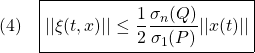
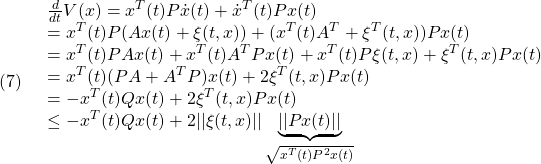
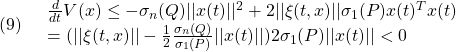
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{c} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] }_{\dot{x}_{E1}(t)} = \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E1}} \underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] }_{x_{E1}(t)} + \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E1}} (u(t)-u_\infty) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-31c37a9934e5cdea3c7a11d0c5575b8d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{\dot{x}_{E2}(t)} = \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E2}} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)} + \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E2}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3876d07fd5a0b32e63fa8f91e20b8ad7_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \left[\begin{array}{c} {\dot x}(t)-w \\ y(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S_E} \left[\begin{array}{c} x(t) \\ u(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-28a64d5f6becf5dc458bf65746e1d706_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \left[\begin{array}{c} -w \\ r \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S_E} \left[\begin{array}{c} x_\infty \\ u_\infty \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-70b5e47d55a371255ff67868bd470bbe_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S_E} \underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d19845bc6a9ba5e6b6ffcc474aa170e5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{\dot{x}_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} \underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e12324e6656148ca4b9a647055b6df5a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E2}} \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S_E} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S_E} \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-790b5d3825c0777b3d3285e5fd6b1394_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E2}} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S_E} \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E3}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c15c3050bb3a9a40764927acc7268c81_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \underbrace{ \left[\begin{array}{cc} 0 & I_m \end{array}\right] }_{C_{E2}} \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S_E} = \underbrace{ \left[\begin{array}{cc} C & 0 \end{array}\right] }_{C_{E3}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fa6e5db5cb4e863339f8797520d1a2b2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot{x}_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} + \underbrace{ \left[\begin{array}{c} 0\\ I_m \end{array}\right] }_{B_{E3}} {\dot u}(t)\\ (x_1(t)=x(t)-x_\infty, x_2(t)=u(t)-u_\infty) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-245a3ce1c7bbd57f344bac4b6ccdca9c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} \ (M=S_2^{-1}S_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cdba45c2f46a4ded8109c4031c43eef8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ -S_2^{-1}S_1 & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-272d89e0452752b99489c956de386a73_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{x}'_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ \bar{A}_{21} & \bar{A}_{22} \\ \end{array}\right] }_{T_sA_{E3}T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} + \underbrace{ \left[\begin{array}{cc} 0\\ S_2 \end{array}\right] }_{T_sB_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5ab2f4f17de6fee9605aa2556d7f248c_l3.png)
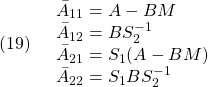
![Rendered by QuickLaTeX.com \displaystyle{(21)\quad \begin{array}{lll} V(\bar{x})= \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]^T }_{\bar{x}^T(t)} \underbrace{ \left[\begin{array}{cc} P_1 & 0\\ 0 & P_2 \end{array}\right] }_{P} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)}\\ \Rightarrow \dot{V}(\bar{x})\le - \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]^T }_{\bar{x}^T(t)} \underbrace{ \left[\begin{array}{cc} Q_1 & 0\\ 0 & I \end{array}\right] }_{Q} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7c77aa3ff56d9793c30ad999001a2185_l3.png)
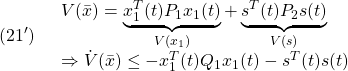
![Rendered by QuickLaTeX.com \displaystyle{(22)\quad \begin{array}{l} s(t)=0\Rightarrow\dot{s}(t)=0 \Rightarrow 0=\bar{A}_{21}x_1(t)+\bar{A}_{22}s(t)+S_2{\dot u}(t)\\ \Rightarrow {\dot u}_{eq}(t)=-\underbrace{S_2^{-1}}_{(SB_{E3})^{-1}} \underbrace{\left[\begin{array}{cc} \bar{A}_{21} & \bar{A}_{22} \\ \end{array}\right]x'_{E3}(t)}_{SA_{E3}x_{E3}(t)}} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3ad4a24162e39c9dd7341a0db806bc67_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(23)\quad \begin{array}{l} {\dot u}_\ell(t)=-\underbrace{S_2^{-1}}_{(SB_{E3})^{-1}} \underbrace{(\left[\begin{array}{cc} \bar{A}_{21} & \bar{A}_{22} \\ \end{array}\right]x'_{E3}(t)-\Phi s(t))}_{(SA_{E3}-\Phi S)x_{E3}(t)}} \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4da62d9774c6809e24338ce1ff05a030_l3.png)
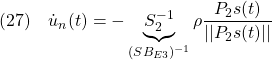
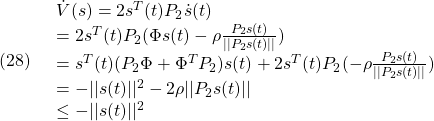
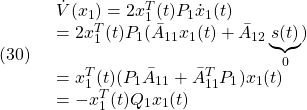
![Rendered by QuickLaTeX.com \displaystyle{(35)\quad {\dot u}_\ell(t)=- \underbrace{ (SB_{E3})^{-1}(SA_{E3}-\Phi S)S_E^{-1} }_{\left[\begin{array}{cc} F & F_I \end{array}\right]} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-edb851ab679593bf698b480644ba82ce_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(37)\quad {\dot u}_n(t) =-S_2^{-1}\rho\, {\rm sgn}( \underbrace{ P_2SS_E^{-1} }_{\left[\begin{array}{cc} G & G_I \end{array}\right]} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)}) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-913747aecf41d0c7b9c2a72e8ab5d520_l3.png)
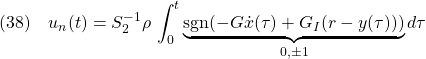
![Rendered by QuickLaTeX.com \displaystyle{(39)\quad \begin{array}{l} \underbrace{\dot{x}_1(t)}_{\dot{x}(t)}=\underbrace{(A-BM)}_{\bar{A}_{11}}x_1(t)+\underbrace{BS_2^{-1}}_{\bar{A}_{12}}\underbrace{(S_1x_1(t)+S_2x_2(t))}_{s(t)}\\ =(A-BM)x_1(t)+BS_2^{-1}S_2(Mx_1(t)+x_2(t))\\ =Ax_1(t)+Bx_2(t)\\ =Ax(t)+Bu(t)-\left[\begin{array}{cc} A & B \end{array}\right] \left[\begin{array}{c} x_\infty \\ u_\infty \end{array}\right]\\ =Ax(t)+Bu(t)-\left[\begin{array}{cc} A & B \end{array}\right]S_E^{-1} \left[\begin{array}{c} -w \\ r \end{array}\right]\\ =Ax(t)+Bu(t)-\left[\begin{array}{cc} I & 0 \end{array}\right] \left[\begin{array}{c} -w \\ r \end{array}\right]\\ =Ax(t)+Bu(t)+w \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2ba4e67edf54d3b4672c514eba81c975_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(109)\quad \left[\begin{array}{c} -w \\ r \end{array}\right] = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right] }_{S_E} \left[\begin{array}{c} x_\infty \\ u_\infty \end{array}\right] \Rightarrow \left[\begin{array}{c} x_\infty \\ u_\infty \end{array}\right]= \left[\begin{array}{c} r \\ -w \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b6f19bc137b345cd02f056ded5359628_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(111)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{\dot{x}_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right] }_{A_{E3}} \underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-39ef4e33ccbbc6089ea56a80794721bd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(116)\quad s(t)= \underbrace{ \left[\begin{array}{cc} s_1 & s_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{s_2 \left[\begin{array}{cc} m & 1 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} \ (m=s_2^{-1}s_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0f6d44c1de2bf58be8fa0712e50791dd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(117)\quad \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} 1 & 0 \\ s_1 & s_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} 1 & 0 \\ -s_2^{-1}s_1 & s_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ae2c14797a0013427aaf5c62507328fe_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(118)\quad \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{x}'_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} -m & s_2^{-1} \\ -s_1m & m \\ \end{array}\right] }_{T_sA_{E3}T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} + \underbrace{ \left[\begin{array}{cc} 0\\ s_2 \end{array}\right] }_{T_sB_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-09497ea1301736f936b51225906c697c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(123)\quad \begin{array}{l} {\dot u}_\ell(t)= -\underbrace{s_2^{-1}}_{(SB_{E3})^{-1}} \underbrace{(\left[\begin{array}{cc} -s_1m & m \\ \end{array}\right]x'_{E3}(t)-\Phi s(t))}_{(SA_{E3}-\Phi S)x_{E3}(t)}}\\ =-s_2^{-1}(\left[\begin{array}{cc} 0 & ms_2 \\ \end{array}\right]- \left[\begin{array}{cc} \Phi s_1 & \Phi s_2 \\ \end{array}\right])x_{E3}(t)\\ =-s_2^{-1}\left[\begin{array}{cc} -\Phi s_1 & ms_2-\Phi s_2 \\ \end{array}\right]x_{E3}(t)\\ =-\left[\begin{array}{cc} -\Phi m & m-\Phi \\ \end{array}\right] \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right] }_{S_E^{-1}} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)}\\ =-\underbrace{(m-\Phi)}_{f}{\dot x}(t)+\underbrace{m(-\Phi)}_{f_I}(r-y(t))\\ \Rightarrow u_\ell(t)=-fx(t)+f_I\int_0^t (r-y(\tau))d\tau \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6aa7495d1adfe2e01b76d9d8229028e7_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(127)\quad \begin{array}{l} {\dot u}_n(t) =-s_2^{-1}\rho\, {\rm sgn}(\underbrace{-\frac{1}{2}\Phi^{-1}}_{p_2} \underbrace{ \left[\begin{array}{cc} s_1 & s_2 \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right] }_{S_E^{-1}} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)})\\ =\rho\, {\rm sgn}(\frac{1}{2}\Phi^{-1} \left[\begin{array}{cc} 1 & m \end{array}\right] \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right])\\ =\rho\, {\rm sgn}(-\underbrace{\frac{1}{2}(-\Phi^{-1})}_{g}{\dot x}(t)+\underbrace{\frac{1}{2}m(-\Phi^{-1})}_{g_I} (r-y(t)))\\ \Rightarrow u_n(t)=\rho\,\int_0^t\underbrace{{\rm sgn}(-g{\dot x}(\tau)+g_I(r-y(\tau)))}_{0,\pm 1}d\tau \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c70ad4d12c7dc10a4700d71c3c2e1719_l3.png)

![Rendered by QuickLaTeX.com \displaystyle{(201)\quad \begin{array}{l} \dot{x}(t)= \underbrace{\left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right]}_{A}x(t) +\underbrace{\left[\begin{array}{cc} 0 \\ 1 \end{array}\right]}_{B}u(t)+ \left[\begin{array}{cc} 0 \\ w \end{array}\right]\\ y(t)=\underbrace{\left[\begin{array}{cc} 1 & 0 \end{array}\right]}_{C}x(t)\\ \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ef113f64e22350dbc52f15182fe1a509_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(209)\quad \left[\begin{array}{c} 0 \\ -w \\ r \end{array}\right] = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{array}\right] }_{S_E} \left[\begin{array}{c} x_{1\infty} \\ x_{2\infty} \\ u_\infty \end{array}\right] \Rightarrow \left[\begin{array}{c} x_{1\infty} \\ x_{2\infty} \\ u_\infty \end{array}\right]= \left[\begin{array}{c} r \\ 0 \\ -w \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-69beeb3b2a284a9be405782120deebbd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(211)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{\dot{x}_{E3}(t)} = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{array}\right] }_{A_{E3}} \underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\right] }_{B_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8e4db6573d9c0866d2409fc3290742b8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(216)\quad \begin{array}{l} s(t)= \underbrace{ \left[\begin{array}{ccc} s_{11} & s_{12} & s_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{s_2 \left[\begin{array}{ccc} m_1 & m_2 & 1 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)}\\ (m_1=s_2^{-1}s_{11},m_2=s_2^{-1}s_{12}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-400eb3876781e6270ec0fdecd65c935f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(217)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} = \underbrace{ \left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ s_{11} & s_{12} & s_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)}\Leftrightarrow\\ \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{ \left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ -s_2^{-1}s_{11} & -s_2^{-1}s_{12} & s_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-967eb06bf641a92d51f2f5dc0823ae03_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(218)\quad \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{x}'_{E3}(t)} = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0\\ -m_1 & -m_2 & s_2^{-1} \\ -s_{12}m_1 & -s_{12}m_2 & m_2 \end{array}\right] }_{T_sA_{E3}T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} + \underbrace{ \left[\begin{array}{cc} 0\\ 0\\ s_2 \end{array}\right] }_{T_sB_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c09c2a528765c494ea49b0e4d526131e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(223)\quad \begin{array}{l} {\dot u}_\ell(t)= -\underbrace{s_2^{-1}}_{(SB_{E3})^{-1}} \underbrace{(\left[\begin{array}{ccc} -s_{12}m_1 & -s_{12}m_2 & m_2 \\ \end{array}\right]x'_{E3}(t)-\Phi s(t))}_{(SA_{E3}-\Phi S)x_{E3}(t)}}\\ =-s_2^{-1}(\left[\begin{array}{ccc} 0 & 0 & m_2s_2 \\ \end{array}\right]- \left[\begin{array}{ccc} \Phi s_{11} & \Phi s_{12} & \Phi s_2 \\ \end{array}\right])x_{E3}(t)\\ =-s_2^{-1}\left[\begin{array}{ccc} -\Phi s_{11} & -\Phi s_{12} & m_2s_2-\Phi s_2 \\ \end{array}\right]x_{E3}(t)\\ =-\left[\begin{array}{ccc} -\Phi m_1 & -\Phi m_2 & m_2-\Phi \\ \end{array}\right] \underbrace{ \left[\begin{array}{ccc} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{array}\right] }_{S_E^{-1}} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)}\\ =-\underbrace{ \left[\begin{array}{cc} -\Phi m_2 & m_2-\Phi \\ \end{array}\right] }_{F}{\dot x}(t)+\underbrace{m_1(-\Phi)}_{F_I}(r-y(t))\\ \Rightarrow u_\ell(t)=-Fx(t)+F_I\int_0^t (r-y(\tau))d\tau \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a5fdce03c67f7578c2ac49db1237f4df_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(237)\quad \begin{array}{l} {\dot u}_n(t) =-s_2^{-1}\rho\, {\rm sgn}(\underbrace{-\frac{1}{2}\Phi^{-1}}_{p_2} \underbrace{ \left[\begin{array}{ccc} s_{11} & s_{12} & s_2 \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{ccc} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{array}\right] }_{S_E^{-1}} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)})\\ =s_2^{-1}\rho\, {\rm sgn}(\frac{1}{2}\Phi^{-1} \left[\begin{array}{ccc} s_{12} & s_2 & s_{11} \end{array}\right] \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right])\\ =\rho\, {\rm sgn}(\frac{1}{2}\Phi^{-1} \left[\begin{array}{ccc} m_2 & 1 & m_1 \end{array}\right] \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right])\\ =\rho\, {\rm sgn}(-\underbrace{\frac{1}{2}(-\Phi^{-1}) \left[\begin{array}{cc} m_2 & 1 \end{array}\right] }_{G}{\dot x}(t)+\underbrace{\frac{1}{2}m_1(-\Phi^{-1})}_{G_I} (r-y(t)))\\ \Rightarrow u_n(t)=\rho\,\int_0^t\underbrace{{\rm sgn}(-G{\dot x}(\tau)+G_I(r-y(\tau)))}_{0,\pm 1}d\tau \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fb6f2c2d66db55b55c3690dbc77615f3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} \dot{x}(t)=Ax(t)+Bu(t)\\ x(t)= \left[\begin{array}{ll} \theta & pitch\ angle\\ q & pitch\ rate\\ \alpha & angle\ of\ atack\\ \eta & elevator\ deflection\\ \delta & flap\ deflection \end{array}\right],\quad u(t)= \left[\begin{array}{ll} \eta_c & elevator\ command\\ \delta_c& flap\ comannd \end{array}\right]\\ A=\left[\begin{array}{rrrrr} 0 & 1 & 0 & 0 & 0\\ 0 &-1.99 & -13.41 & -18.95 & -3.60\\ 0 & 1 & -1.74 & -0.08 & -0.59\\ 0 & 0 & 0 & -20 & 0\\ 0 & 0 & 0 & 0 & -20 \end{array}\right],\quad B=\left[\begin{array}{rr} 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 20 & 0\\ 0 & 20 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e8e30c3e5083c206da3951e3e40e9cfb_l3.png)

![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \begin{array}{l} \dot{x}(t)=Ax(t)+Bu(t)\\ x(t)= \left[\begin{array}{ll} \gamma=\theta-\alpha & fligt\ path\ angle\\ q & pitch\ rate\\ \alpha & angle\ of\ atack\\ \eta & elevator\ deflection\\ \delta & flap\ deflection \end{array}\right],\quad u(t)= \left[\begin{array}{ll} \eta_c & elevator\ command\\ \delta_c& flap\ comannd \end{array}\right]\\ A=\left[\begin{array}{rrrrr} 0 & 0 & 1.74 & 0.08 & 0.59\\ 0 &-1.99 & -13.41 & -18.95 & -3.60\\ 0 & 1 & -1.74 & -0.08 & -0.59\\ 0 & 0 & 0 & -20 & 0\\ 0 & 0 & 0 & 0 & -20 \end{array}\right],\quad B=\left[\begin{array}{rr} 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 20 & 0\\ 0 & 20 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b3ae110ebe0cc483c67a6db0b309e181_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} y(t)=Hx(t)\\ H= \left[\begin{array}{ccccc} 1 & 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c44cf07d269341a588b528f5aca4caf9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(20)\quad { \boxed{\begin{array}{l} u(t)=u_\ell(t)+u_n(t)\\ u_\ell(t)=-\underbrace{(SB_E)^{-1}(SA_E-\Phi S)}_{L=L_{eq}+L_\Phi}\left[\begin{array}{c} x_r(t)\\ x(t) \end{array}\right]\\ -\underbrace{(SB_E)^{-1}(\Phi S_r+S_1B_r)}_{L_r} r(t) +\underbrace{(SB_E)^{-1}S_r}_{L_{\dot r}} \dot{r}(t)\\ u_n(t)=-\underbrace{(SB_E)^{-1}\rho(t,x)}_{L_n}\frac{P_2(s(t)-S_rr(t))}{||P_2(s(t)-S_rr(t))||} \end{array}}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-adc6bfdf1b50ea9ed3b1152bc4ee1729_l3.png)
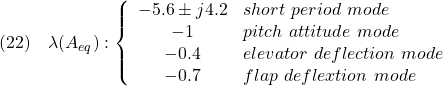
![Rendered by QuickLaTeX.com \displaystyle{(23)\quad {\tt specpos}= \left[\begin{array}{ccccc} 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\\hline 1 & 1 & 1 & 1 & 1\\ 1 & 0 & 1 & 1 & 1\\ 0 & 1 & 1 & 0 & 1\\\hline 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\ \end{array}\right],\quad {\tt specent}= \left[\begin{array}{rrrrr} -1 & -1 & -1 & -1 & -1\\ -1 & -1 & -1 & -1 & -1\\\hline 0 & 0 & 1 & 0 & 1\\ 1 & -1 & 0 & 1 & 0\\ -1 & 1 & 0 & -1 & 0\\\hline -1 & -1 & -1 & -1 & -1\\ -1 & -1 & -1 & -1 & -1\\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0c718bed933ebbd16e58b62392705e36_l3.png)
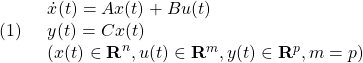
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \left[\begin{array}{c} \dot x_r(t)\\ \dot x(t) \end{array}\right] = \left[\begin{array}{c|cc} 0 & -C_1 & -C_2\\\hline 0 & A_{11} & A_{12} \\ 0 & A_{21} & A_{22} \end{array}\right] \left[\begin{array}{c} x_r(t)\\ x(t) \end{array}\right] + \left[\begin{array}{c} 0\\\hline 0\\ B_2 \end{array}\right] u(t) + \left[\begin{array}{c} I_m \\\hline 0 \\ 0 \end{array}\right] r(t)\\ (x_r(t)\in{\rm\bf R}^m, x(t)\in{\rm\bf R}^n) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1ab4b378422eddd1bff475a2408082e2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5a)\quad \begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc|c} 0 & -C_1 & -C_2\\ 0 & A_{11} & A_{12} \\\hline 0 & A_{21} & A_{22} \end{array}\right] }_{A_E} \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0\\ 0\\\hline B_2 \end{array}\right] }_{B_E} u(t) + \left[\begin{array}{c} I_m \\ 0 \\\hline 0 \end{array}\right] r(t)\\ (x_1(t)\in{\rm\bf R}^n, x_2(t)\in{\rm\bf R}^m) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-374491b693fbc08a0a4648abd3e610d2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} %\underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] %}_{x(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I_m \\ \end{array}\right] }_{S} %\underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] %}_{x(t)} \ (M=S_2^{-1}S_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-01bb686061b94fbab2a0ff90e7d23f64_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} I_n & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right]\\ \Leftrightarrow \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} I_n & 0 \\ -S_2^{-1}S_1 & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-19e5643bcb296d8a517aba35bc4fe14e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8a)\quad \begin{array}{l} %\underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] %}_{\dot{x}'(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ S_2\bar{A}_{21} & S_2\bar{A}_{22}S_2^{-1} \\ \end{array}\right] }_{T_sA_ET_s^{-1}} %\underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] %}_{x'(t)} + \underbrace{ \left[\begin{array}{cc} 0\\ S_2B_2 \end{array}\right] }_{T_sB_E} u(t)\\ + \left[\begin{array}{cc} B_r \\ S_1B_r \end{array}\right] r(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a23595fe93cd3fb99284c6e90f61bcf1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8b)\quad \left\{\begin{array}{l} \bar{A}_{11}= \left[\begin{array}{cc} 0 & -C_1 \\ 0 & A_{11} \end{array}\right] -\left[\begin{array}{c} -C_2\\ A_{12} \end{array}\right]M\\ \bar{A}_{12}= \left[\begin{array}{c} -C_2\\ A_{12} \end{array}\right]S_2^{-1}\\ \bar{A}_{21}=S_2(M\bar{A}_{11} + \left[\begin{array}{cc} 0 & A_{21} \end{array}\right] -A_{22}M)\\ \bar{A}_{22}=S_2(M \left[\begin{array}{c} -C_2\\ A_{12} \end{array}\right] +A_{22})S_2^{-1}\\ B_r=\left[\begin{array}{cc} I_m \\ 0 \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-24d62178408415d07b9cef2c8d0cfab3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \boxed{ \begin{array}{lll} V(\bar{x})= \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t)-S_rr(t) \end{array}\right]^T }_{\bar{x}^T(t)} \underbrace{ \left[\begin{array}{cc} P_1 & 0\\ 0 & P_2 \end{array}\right] }_{P} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t)-S_rr(t) \end{array}\right] }_{\bar{x}(t)}\\ \Rightarrow \dot{V}(\bar{x})\le - \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t)-S_rr(t) \end{array}\right]^T }_{\bar{x}^T(t)} \underbrace{ \left[\begin{array}{cc} Q_1 & 0\\ 0 & I \end{array}\right] }_{Q} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t)-S_rr(t) \end{array}\right] }_{\bar{x}(t)} \end{array}}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-174b6e0b351e183151b07a67d25fe6dc_l3.png)
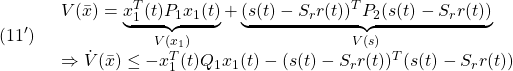
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{cl} (12.1) & s(t)=0\\ \Downarrow &\\ (12.2) & \dot{s}(t)=0\\ \Downarrow &\\ (12.3) & 0=S_2\bar{A}_{21}x_1(t)+S_2\bar{A}_{22}S_2^{-1}s(t)+S_2B_2u(t)\\ \Downarrow &\\ (12.4) & u_{eq}(t)=-\underbrace{(S_2B_2)^{-1}}_{([0\ I]T_sB_E)^{-1}} \underbrace{\left[\begin{array}{cc} S_2\bar{A}_{21} & S_2\bar{A}_{22}S_2^{-1} \\ \end{array}\right]}_{[0\ I]T_sA_ET_s^{-1}} \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]\\ \Downarrow & by\ S=[0\ I]T_s\\ (12.5) & u_{eq}(t)=-(SB_E)^{-1}SA_ET_s^{-1} \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]\\ \Downarrow & by\ (7),(8b)\\ (12.6) & u_{eq}(t)=-(SB_E)^{-1}SA_E \left[\begin{array}{c} x_r(t)\\ x(t) \end{array}\right]} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fc541c88c94f46e054237f8c4eb58974_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \begin{array}{l} u_\ell(t)=-(S_2B_2)^{-1} (\left[\begin{array}{cc} S_2\bar{A}_{21} & S_2\bar{A}_{22}S_2^{-1} \\ \end{array}\right]\left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]-\Phi s(t))\\ -(S_2B_2)^{-1}(\Phi S_r+S_1B_r)r(t)+(S_2B_2)^{-1}S_r\dot{r}(t)\\ \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-523e59ff1e3266a531c8f91b270e4fc0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(13')\quad { \boxed{\begin{array}{l} u_\ell(t) =-\underbrace{(SB_E)^{-1}(SA_E-\Phi S)}_{L=L_{eq}+L_\Phi}\left[\begin{array}{c} x_r(t)\\ x(t) \end{array}\right]\\ -\underbrace{(SB_E)^{-1}(\Phi S_r+S_1B_r)}_{L_r} r(t) +\underbrace{(SB_E)^{-1}S_r}_{L_{\dot r}} \dot{r}(t)\\ \end{array}}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2d8158c14705344b0d2033bddb8e59ac_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \begin{array}{l} \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] = \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ S_2\bar{A}_{21} & S_2\bar{A}_{22}S_2^{-1} \\ \end{array}\right] \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]\\ + \left[\begin{array}{cc} 0\\ S_2B_2 \end{array}\right] (-(S_2B_2)^{-1} (\left[\begin{array}{cc} S_2\bar{A}_{21} & S_2\bar{A}_{22}S_2^{-1} \\ \end{array}\right]\left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]-\Phi s(t))\\ -(S_2B_2)^{-1}(\Phi S_r+S_1B_r)r(t)+(S_2B_2)^{-1}S_r\dot{r}(t)+u_n(t)) + \left[\begin{array}{cc} B_r \\ S_1B_r \end{array}\right] r(t)\\ = \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ S_2\bar{A}_{21} & S_2\bar{A}_{22}S_2^{-1} \\ \end{array}\right] \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]\\ + \left[\begin{array}{cc} 0\\ I_m \end{array}\right] \left[\begin{array}{cc} -S_2\bar{A}_{21} & -S_2\bar{A}_{22}S_2^{-1}+\Phi \\ \end{array}\right] \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]\\ + \left[\begin{array}{cc} 0\\ -(\Phi S_r+S_1B_r)r(t)+S_r\dot{r}(t)+S_2B_2u_n(t) \end{array}\right] + \left[\begin{array}{cc} B_r \\ S_1B_r \end{array}\right] r(t)\\ = \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ 0 & \Phi \\ \end{array}\right] \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]+ \left[\begin{array}{cc} B_rr(t)\\ -\Phi S_rr(t)+S_r\dot{r}(t)+S_2B_2u_n(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7299445c3fbe65641193f7a4c068b664_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{s}(t)-S_r\dot{r}(t) \end{array}\right] = \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ 0 & \Phi \\ \end{array}\right] \left[\begin{array}{c} x_1(t)\\ s(t)-S_rr(t) \end{array}\right]\\ + \left[\begin{array}{cc} B_rr(t)\\ -\Phi S_rr(t)+S_r\dot{r}(t)+S_2B_2u_n(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2cbbaf4d3607cc033e3ec653af8d867e_l3.png)
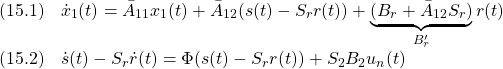
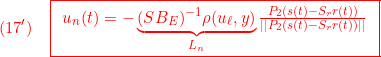
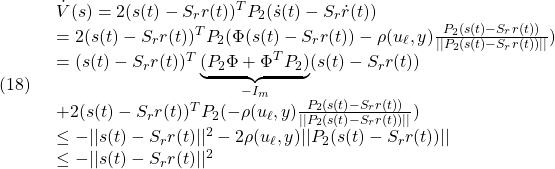
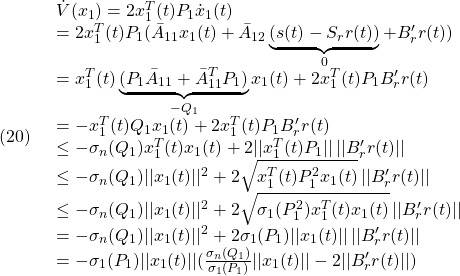


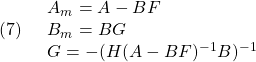
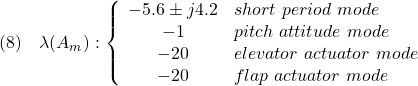
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad {\tt specpos}= \left[\begin{array}{ccc|cc} 1 & 1 & 1 & 0 & 0\\ 1 & 0 & 1 & 0 & 0\\ 0 & 1 & 1 & 0 & 0\\\hline 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\\ \end{array}\right],\quad {\tt specent}= \left[\begin{array}{rrr|rr} 0 & 0 & 1 & -1 & -1\\ 1 & -1 & 0 & -1 & -1\\ -1 & 1 & 0 & -1 & -1\\\hline -1 & -1 & -1 & 1 & -1\\ -1 & -1 & -1 & -1 & 1\\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9351aa1713d68cc420ab75e44c211a51_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{l} F=WV^{-1} =\left[\begin{array}{rrrrr} -1.9338 & -0.5744 & -2.1188 & 0.4750 & 0.1066\\ 1.9571 & 0.2253 & 3.1273 & -0.0694 & -0.0515 \end{array}\right]\\ W=\left[\begin{array}{rrrrr} 0.8445 & 1.9935 & -0.2742 & 0 & 0\\ -2.7055 & 1.2780 & 0.1767 & 0 & 0 \end{array}\right]\\ V=\left[\begin{array}{rrrrr} 0 & -0.0000 & 0.6667 & 0.0030 & -0.0313\\ 1.0000 & -9.5000 & -0.3333 & 0.9964 & 0.1493\\ -0.9286 & 1.0000 & -0.3333 & -0.0528 & 0.0238\\ -1.8252 & -2.2364 & 0.2886 & 1.0000 & -0.0649\\ 2.9860 & -2.6459 & -0.1860 & -0.0825 & 1.0000 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b86eb8a3dc0f557c2de880c6fc23d3ee_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad \underbrace{ \left[\begin{array}{rr} 0.025 & 0\\ 0 & 0.025 \end{array}\right] }_{P_2} \underbrace{ \left[\begin{array}{rr} 20 & 0\\ 0 & 20 \end{array}\right] }_{\Phi} +(*)^T=-I }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dc78c4ca1633a74198c3d266be410408_l3.png)
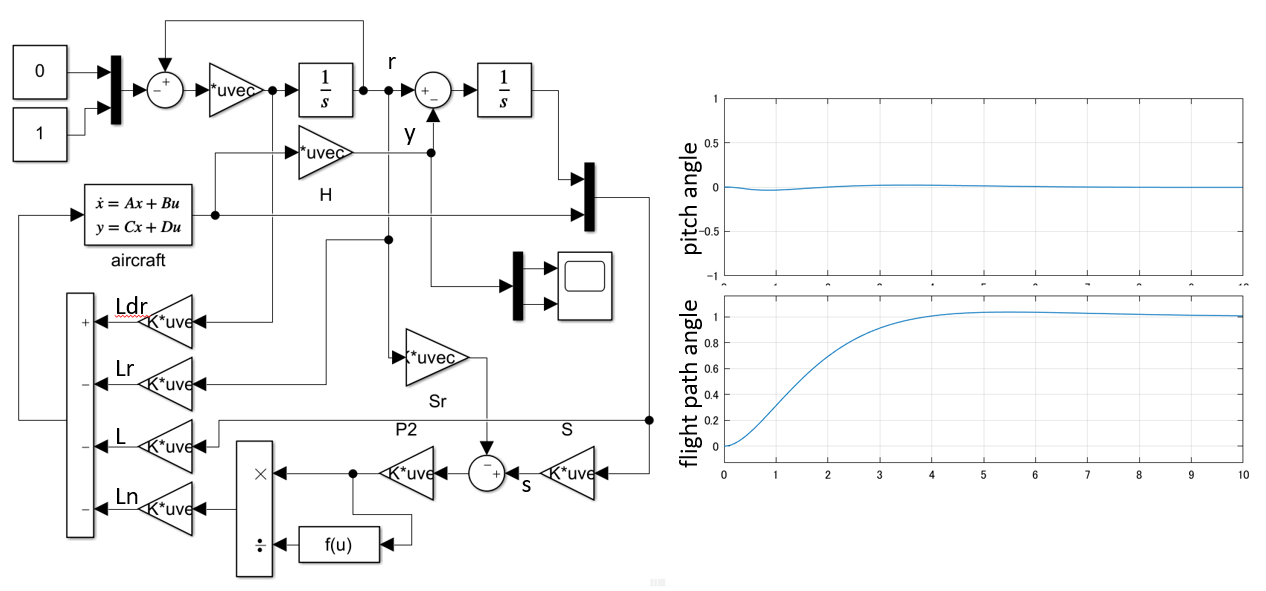
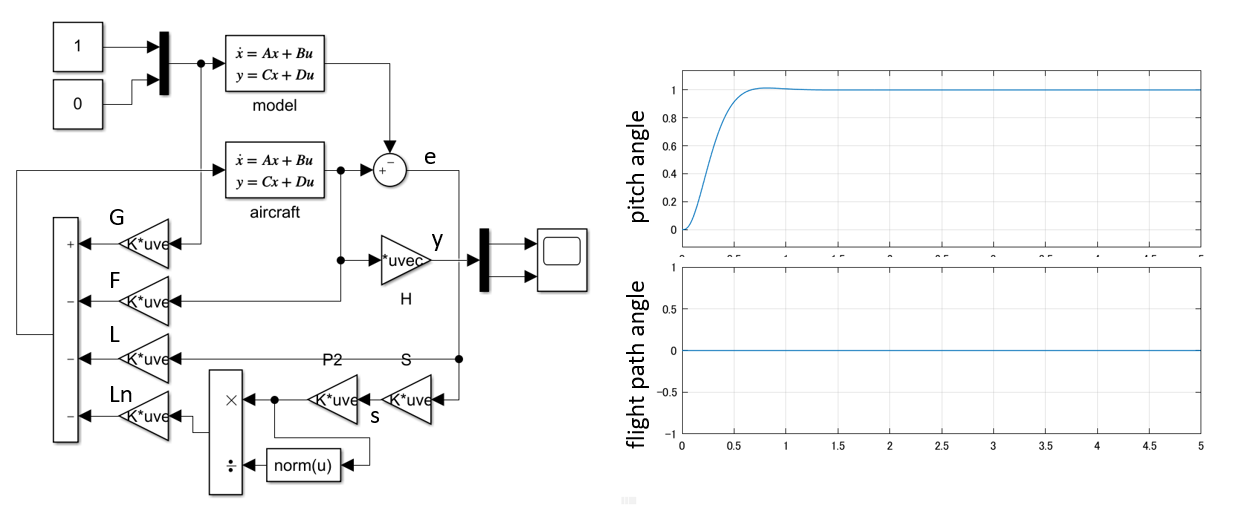 図2 モデル規範法によるSMC制御系応答
図2 モデル規範法によるSMC制御系応答
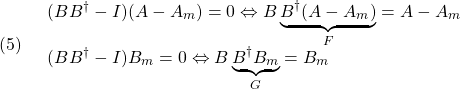
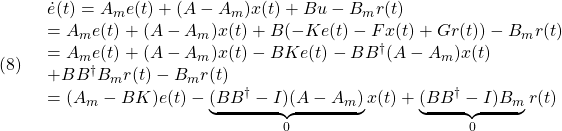
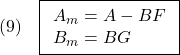
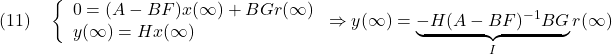
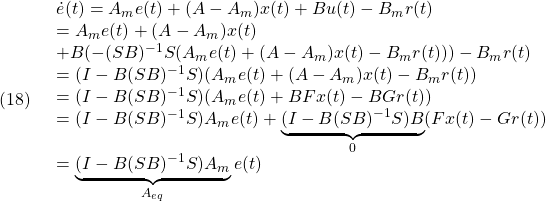
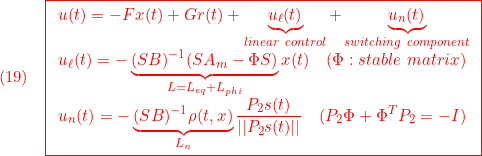
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \dot{x}= \underbrace{ \left[\begin{array}{cc} 0 & 0\\ 0 & -1 \end{array}\right] }_{A} x+ \underbrace{ \left[\begin{array}{cc} 1 & 1\\ 1 & -1 \end{array}\right] }_{B} u }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c745d4f5f1b3d7dfbb8161becd05cbbc_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad %\begin{array}{l} u=- \underbrace{ \left[\begin{array}{cc} 1 & 1\\ 1 & -1 \end{array}\right] }_{F_1} x,\quad u=- \underbrace{ \left[\begin{array}{cc} 1 & 0\\ 1 & 2 \end{array}\right] }_{F_2} x %\end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d49d42d887c347c0b3f6ee06df55f59c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \dot{x}= \underbrace{ \left[\begin{array}{cc} -2 & 0\\ 0 & -3 \end{array}\right] }_{A-BF_1} x,\quad \dot{x}= \underbrace{ \left[\begin{array}{cc} -2 & 2\\ 0 & -3 \end{array}\right] }_{A-BF_2} x }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-93545ea90d73386ffad49fb6770534d9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \dot{x}= \underbrace{ \left[\begin{array}{cc} e^{-2t} & 0\\ 0 & e^{-3t} \end{array}\right] }_{\exp((A-BF_1)t)=V_1\exp(\Lambda t)V_1^{-1}} x(0) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a848c79fb2043d68760134bb59a59432_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \dot{x}= \underbrace{ \left[\begin{array}{cc} 1 & 1\\ 0 & 1 \end{array}\right] \left[\begin{array}{cc} e^{-2t} & 0\\ 0 & e^{-3t} \end{array}\right] \left[\begin{array}{cc} 1 & -1\\ 0 & 1 \end{array}\right] }_{\exp((A-BF_2)t)=V_2\exp(\Lambda t)V_2^{-1}} x(0) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9cfbe60f5937bb40578221b8097e070e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad (A-BF)v=\lambda v \Rightarrow \underbrace{ \left[\begin{array}{cc} \lambda I-A & B \end{array}\right] }_{G(\lambda)} \left[\begin{array}{c} v\\ \xi \end{array}\right] =0 \quad(\xi=Fv) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-54bfb57a51b16a01489326657af0618c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc} 0-(-2) & 0\\ 0 & -1-(-2) \end{array}\right]^{-1} \left[\begin{array}{cc} 1 & 1\\ 1 & -1 \end{array}\right] }_{(A-\lambda I_n)^{-1}B} \xi_1 =\underbrace{ \left[\begin{array}{c} 1\\ 0 \end{array}\right]}_{V_1(:,1)}\\ \Rightarrow \xi_1= \left[\begin{array}{cc} 1/2 & 1/2\\ 1 & -1 \end{array}\right]^{-1} \left[\begin{array}{c} 1\\ 0 \end{array}\right] = \left[\begin{array}{cc} 1 & 1/2\\ 1 & -1/2 \end{array}\right] \left[\begin{array}{c} 1\\ 0 \end{array}\right] = \left[\begin{array}{cc} 1\\ 1 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1b41e93a5933617741e4f586e93e19f7_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc} 0-(-3) & 0\\ 0 & -1-(-3) \end{array}\right]^{-1} \left[\begin{array}{cc} 1 & 1\\ 1 & -1 \end{array}\right] }_{(A-\lambda I_n)^{-1}B} \xi_2 =\underbrace{ \left[\begin{array}{c} 0\\ 1 \end{array}\right]}_{V_1(:,2)}\\ \Rightarrow \xi_2= \left[\begin{array}{cc} 1/3 & 1/3\\ 1/2 & -1/2 \end{array}\right]^{-1} \left[\begin{array}{c} 0\\ 1 \end{array}\right] = \left[\begin{array}{cc} 3/2 & 1\\ 3/2 & -1 \end{array}\right] \left[\begin{array}{c} 0\\ 1 \end{array}\right] = \left[\begin{array}{cc} 1\\ -1 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-acb8eeda9b274090e7fd1446eb642dc3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad \begin{array}{l} (A-BF)(v_R\pm jv_I)=(\lambda_R\pm j\lambda_I)(v_R\pm jv_I)\\ \Rightarrow (A-BF)v_R=\lambda_Rv_R-\lambda_Iv_I,\ (A-BF)v_I =\lambda_Rv_I+\lambda_Iv_R \\ \Rightarrow \underbrace{ \left[\begin{array}{ccc} \lambda_R I-A & \lambda_I I & B \end{array}\right] }_{G(\lambda)} \left[\begin{array}{cc} v_R & v_I\\ -v_I & v_R\\ \xi_R & \xi_I \end{array}\right] =0 \quad(\xi_R=Fv_R,\xi_I=Fv_I) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6d47009b53c361504d7e6bc98f9e71b8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad G(\lambda) \left[\begin{array}{c} N(\lambda)\\ P(\lambda)\\ M(\lambda) \end{array}\right] =0 \Rightarrow \left[\begin{array}{cc} v_R & v_I\\ -v_I & v_R\\ \xi_R & \xi_I \end{array}\right]= \left[\begin{array}{c} N(\lambda)\\ P(\lambda)\\ M(\lambda) \end{array}\right] \left[\begin{array}{cc} \delta_R & \delta_I \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d676d8a341ec09736514abf70264ec37_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(19)\quad \left[\begin{array}{c} v_R \\ v_I \end{array}\right]= \underbrace{ \left[\begin{array}{cc} N(\lambda) \\ -P(\lambda) \end{array}\right] }_{\alpha} \delta_R= \underbrace{ \left[\begin{array}{cc} P(\lambda)\\ N(\lambda) \end{array}\right] }_{\beta} \delta_I }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-abf82ddd7131d916fdee953a63a0709d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(20)\quad \underbrace{ \left[\begin{array}{c} K_\alpha^T\\ K_\beta^T \end{array}\right] }_{\gamma^T} K_\gamma=0 \Rightarrow {\cal R}(K_\gamma)\subset {\cal N}(K_\alpha^T)\cap {\cal N}(K_\beta^T)={\cal R}(\alpha)\cap {\cal R}(\beta) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-70b8648bf35dd1f338dadef1f1f30f76_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(22)\quad \tilde{R}K_\gamma\delta=\tilde{R}v =\left[\begin{array}{c} \tilde{v}_R^s\\ \tilde{v}_I^s\\ \tilde{v}_R^u\\ \tilde{v}_I^u\\ \end{array}\right] \Rightarrow \left[\begin{array}{cc} I_{2q} & 0 \end{array}\right] \tilde{R}K_\gamma\times\delta= \left[\begin{array}{c} \tilde{v}_R^s\\ \tilde{v}_I^s\\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ca6f1cde64789122929ed05b745bf916_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(25)\quad \begin{array}{l} (A-BF)(v_R\pm jv_I)=(\lambda_R\pm j\lambda_I)(v_R\pm jv_I)\\ \Rightarrow (A-BF)v_R=\lambda_Rv_R-\lambda_Iv_I,\ (A-BF)v_I =\lambda_Rv_I+\lambda_Iv_R \\ \Rightarrow %\underbrace{ \left[\begin{array}{cccc} \lambda_R I-A & -\lambda_I I & B & 0\\ \lambda_I I & \lambda_R I-A & 0 & B\\ \end{array}\right] %}_{G(\lambda)} \left[\begin{array}{cc} v_R \\ v_I \\ \xi_R \\ \xi_I \end{array}\right] =0 \quad(\xi_R=Fv_R,\xi_I=Fv_I) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5c3395554ec680982602827ec93699f2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(26)\quad \begin{array}{l} G(\lambda)\leftarrow \left[\begin{array}{cccc} \lambda_R I-A & -\lambda_I I & B & 0\\ \lambda_I I & \lambda_R I-A & 0 & B \end{array}\right]\\ v\leftarrow\left[\begin{array}{c} v_R\\ v_I \end{array}\right],\ \xi\leftarrow\left[\begin{array}{c} \xi_R\\ \xi_I \end{array}\right],\ \delta\leftarrow\left[\begin{array}{c} \delta_R\\ \delta_I \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3836feba6912b5d294cc1fc1bb8ed8ff_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(27)\quad \begin{array}{l} \left[\begin{array}{cc} M_{11} & M_{12} \\ M_{21} & M_{22} \end{array}\right]^{-1} = \left[\begin{array}{cc} \Phi^{-1} & -\Phi^{-1}M_{12}M_{22}^{-1} \\ -M_{22}^{-1}M_{21}\Phi^{-1} & M_{22}^{-1}+M_{22}^{-1}M_{21}\Phi^{-1}M_{12}M_{22}^{-1} \end{array}\right]\\ \Phi\stackrel{\rm def}{=}M_{11}-M_{12}M_{22}^{-1}M_{21}\ (M_{22}\ {\rm nonsingular}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bcdb0550e930a915276eb65efa6b45a9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(29)\quad \begin{array}{l} \left[\begin{array}{cc} \lambda_R I-A & -\lambda_I I\\ \lambda_I I & \lambda_R I-A \end{array}\right] \underbrace{ \left[\begin{array}{cc} \lambda_R I-A & -\lambda_I I\\ \lambda_I I & \lambda_R I-A \end{array}\right]^{-1} \left[\begin{array}{cc} B & 0\\ 0 & B \end{array}\right] }_{N(\lambda)}\\ + \left[\begin{array}{cc} B & 0\\ 0 & B \end{array}\right] \underbrace{(-I_{2m})}_{M(\lambda)}=0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d460a19e80907d9a0b852c5de467ac5e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(30)\quad \boxed{ \left[\begin{array}{c} v_R\\ v_I \end{array}\right] = \left[\begin{array}{cc} A-\lambda_R I & \lambda_I I\\ -\lambda_I I & A-\lambda_R I \end{array}\right]^{-1} \left[\begin{array}{cc} B & 0\\ 0 & B \end{array}\right] \left[\begin{array}{c} \xi_R\\ \xi_I \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-12c74d3d5e932ac7ad3709a3d3e04cd6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(31)\quad \underbrace{ \left[\begin{array}{c} 1\\ 0 \end{array}\right]}_{v_R} \pm j \underbrace{ \left[\begin{array}{c} 0\\ 1 \end{array}\right]}_{v_I} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cf417f6f422bf9420ff045018f997982_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(32)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cccc} 0-(-1) & 0 & 1 & 0\\ 0 & -1-(-1) & 0 & 1\\ -1 & 0 & 0-(-1) & 0\\ 0 & -1 & 0 & -1-(-1) \end{array}\right]^{-1} }_{\left[\begin{array}{cc} A-\lambda_R I & \lambda_I I\\ -\lambda_I I & A-\lambda_R I \end{array}\right]^{-1}}\\ \times\underbrace{ \left[\begin{array}{cccc} 1 & 1 & 0 & 0\\ 1 & -1& 0 & 0\\ 0 & 0 & 1 & 1\\ 0 & 0 & 1 & -1 \end{array}\right] }_{\left[\begin{array}{cc} B & 0\\ 0 & B \end{array}\right]} \left[\begin{array}{c} \xi_R\\ \xi_I \end{array}\right] =\underbrace{ \left[\begin{array}{c} 1\\ 0\\ 0\\ 1 \end{array}\right]}_{\left[\begin{array}{c} v_R\\ v_I \end{array}\right]}\\ \Rightarrow \left[\begin{array}{c} \xi_R\\ \xi_I \end{array}\right]= \left[\begin{array}{cccc} 1/2 & 1/2 & -1/2 & -1/2\\ 0 & 0 & -1 & 1\\ 1/2 & 1/2 & 1/2 & 1/2\\ 1 & -1& 0 & 0 \end{array}\right]^{-1} \left[\begin{array}{c} 1\\ 0\\ 0\\ 1 \end{array}\right]= \left[\begin{array}{c} 1\\ 0\\ -1/2\\ -1/2 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a8c14670356af07d6f9cd11e59a8f1f8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(33)\quad \begin{array}{l} \left[\begin{array}{cc} \xi_R & \xi_I \end{array}\right] =F \left[\begin{array}{cc} v_R & v_I \end{array}\right]\\ \Rightarrow F= \left[\begin{array}{cc} \xi_R & \xi_I \end{array}\right] \left[\begin{array}{cc} v_R & v_I \end{array}\right]^{-1} = \left[\begin{array}{cc} 1 & -1/2\\ 0 & -1/2 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a6a803556df89cc05beca9ed87858cec_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot x(t)} = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a4c8217b8c641b28c9d2c724fc2462cb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} \ (M=S_2^{-1}S_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0639c7053096db5f35e066d8fec1086a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} A_{eq}= \underbrace{ \left[\begin{array}{cc} I & 0 \\ -M & 0 \\ \end{array}\right] }_{I_n-B(SB)^{-1}S} \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right]= \left[\begin{array}{cc} A_{11} & A_{12} \\ -MA_{11} & -MA_{12} \\ \end{array}\right]\\ = \left[\begin{array}{cc} I & 0 \\ -M & I \\ \end{array}\right] \left[\begin{array}{cc} \bar{A}_{11} & A_{12} \\ 0 & 0 \\ \end{array}\right] \left[\begin{array}{cc} I & 0 \\ -M & I \\ \end{array}\right]^{-1} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e3ecd7fa57b5a4b72c9f1811a79dd648_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{x}_{r1}(t)\\ \dot{x}_{r2}(t) \end{array}\right] }_{\dot{x}_r(t)} = \underbrace{ \left[\begin{array}{cc} A_{r11} & A_{r12} \\ A_{r21} & A_{r22} \\ \end{array}\right] }_{A_r=T_rAT_r^T} \underbrace{ \left[\begin{array}{c} x_{r1}(t)\\ x_{r2}(t) \end{array}\right] }_{x_r(t)} + \underbrace{ \left[\begin{array}{c} 0\\ \Sigma_1V^T \end{array}\right] }_{B_r=T_rB} u(t)\\ + \underbrace{ \left[\begin{array}{l} f_{ru}(t,x)\\ f_{rm}(t,x,u) \end{array}\right] }_{f_r(t,x,u)=T_rf(t,x,u)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ffa705d6b2bd55a3734da676f36934df_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_{r1} & S_{r2} \\ \end{array}\right] }_{S_r=ST_r^T} \underbrace{ \left[\begin{array}{c} x_{r1}(t)\\ x_{r2}(t) \end{array}\right] }_{x_r(t)=T_rx(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5f1e30d6fccc2ee648cf30ffd07ad4c3_l3.png)
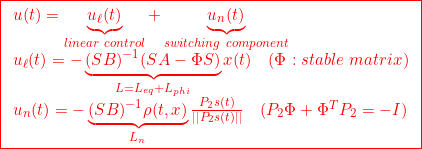
 図1 台車駆動型倒立振子
図1 台車駆動型倒立振子