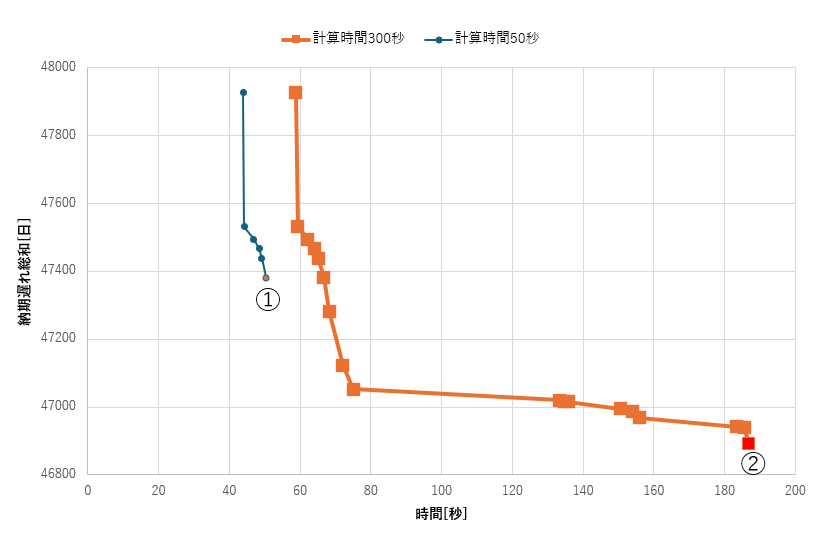
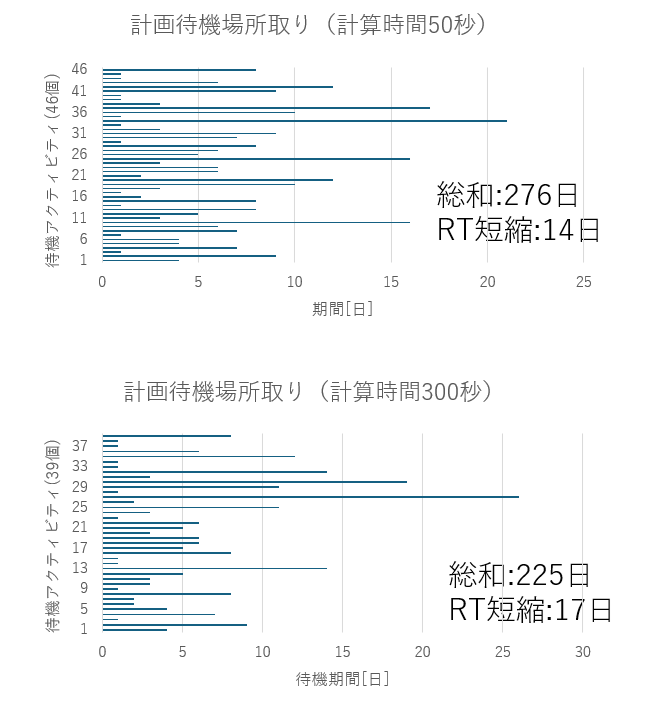
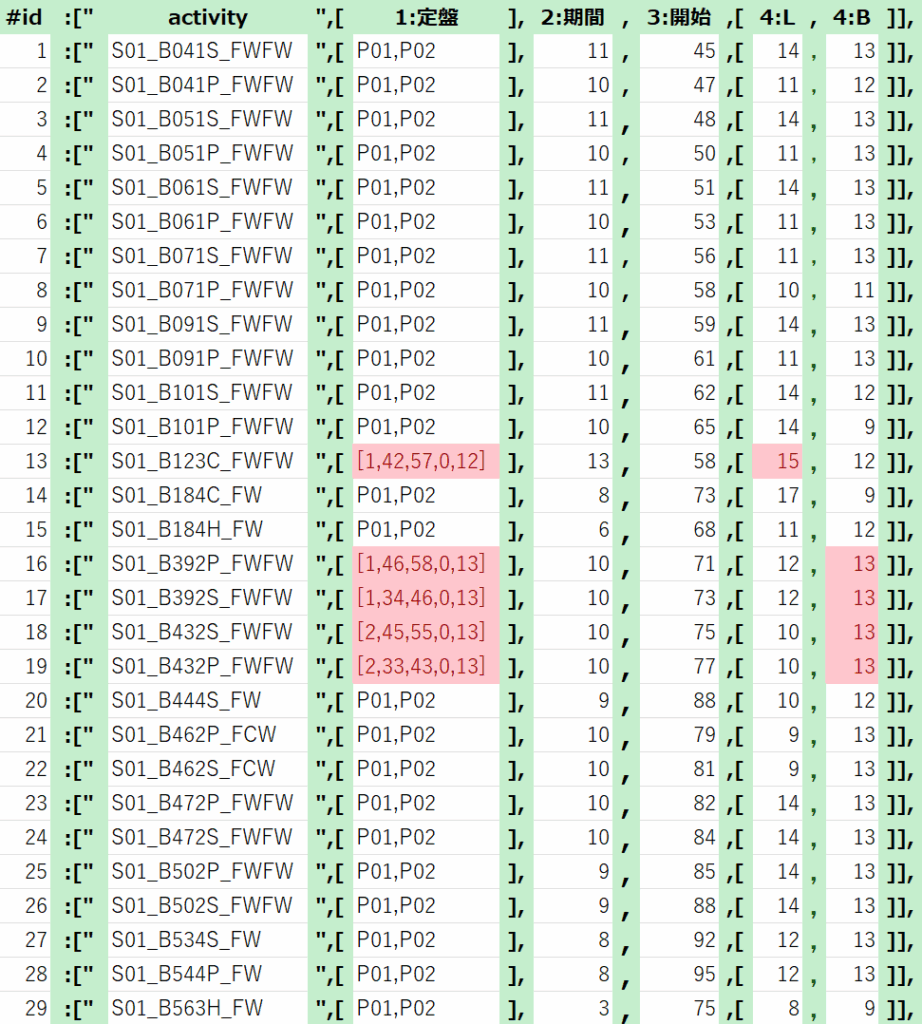
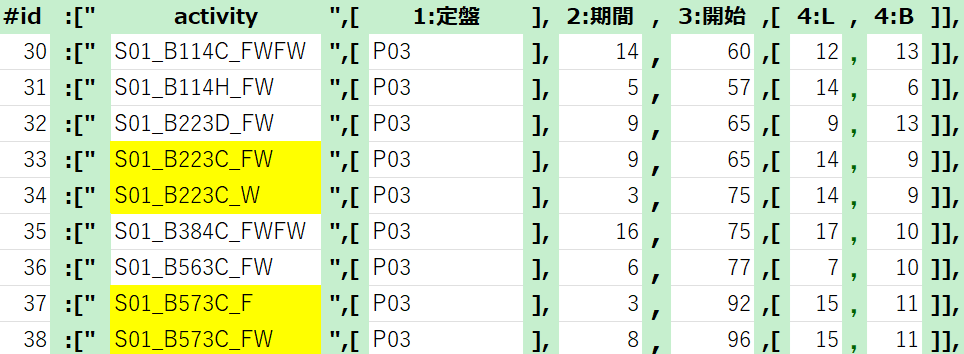
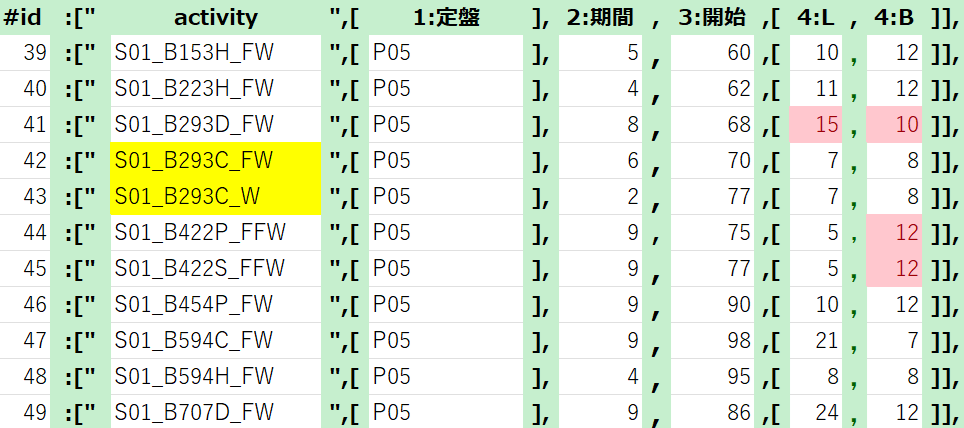
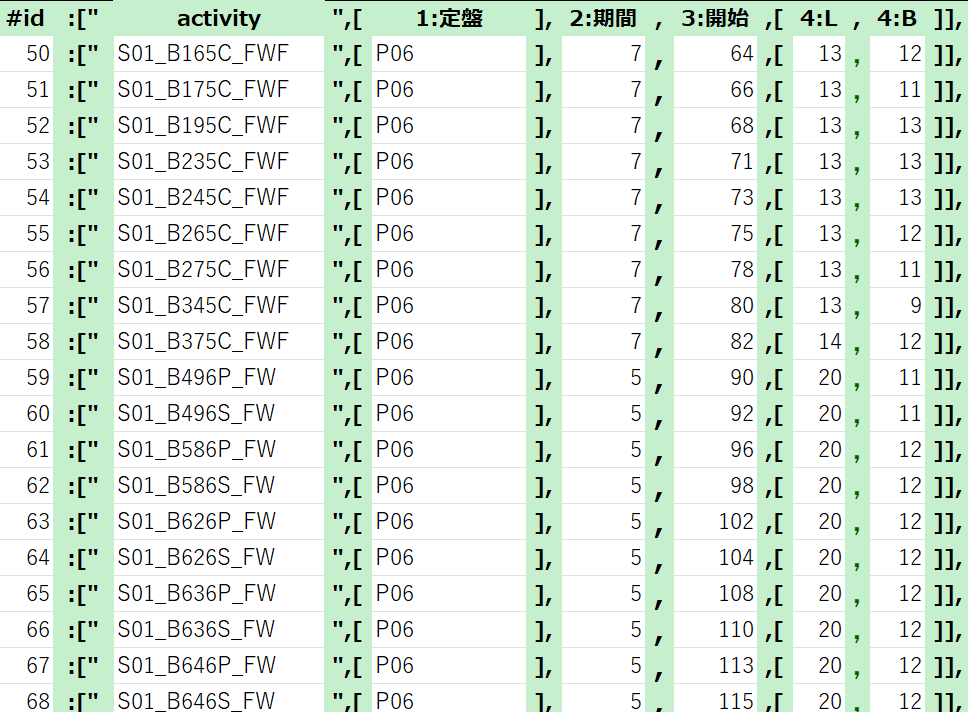
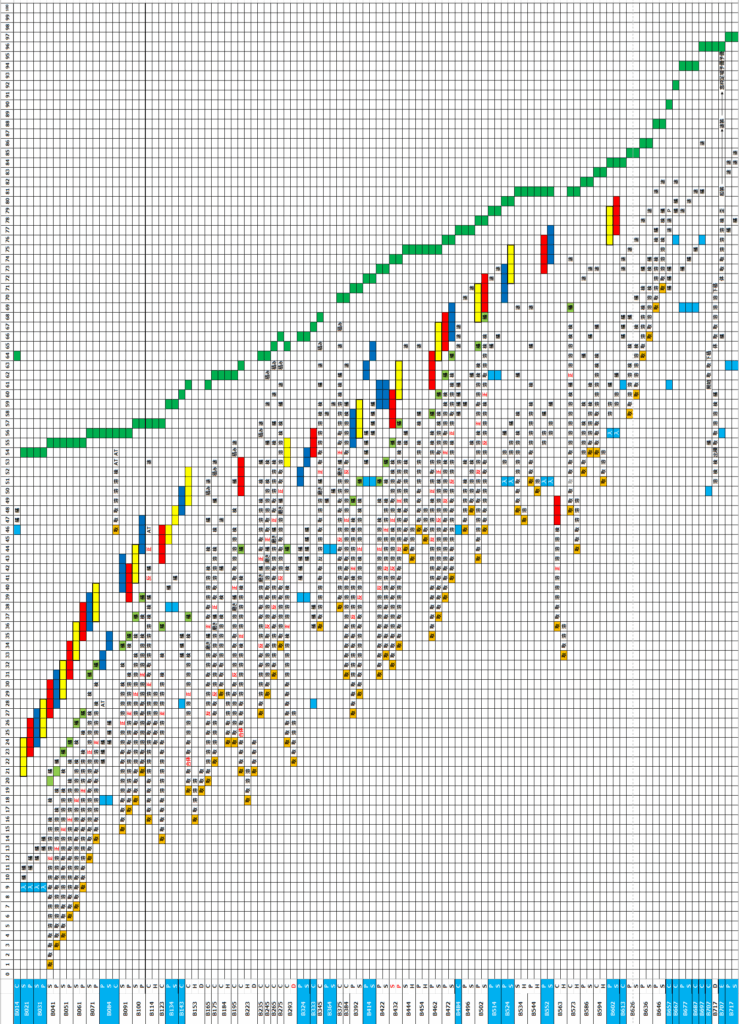
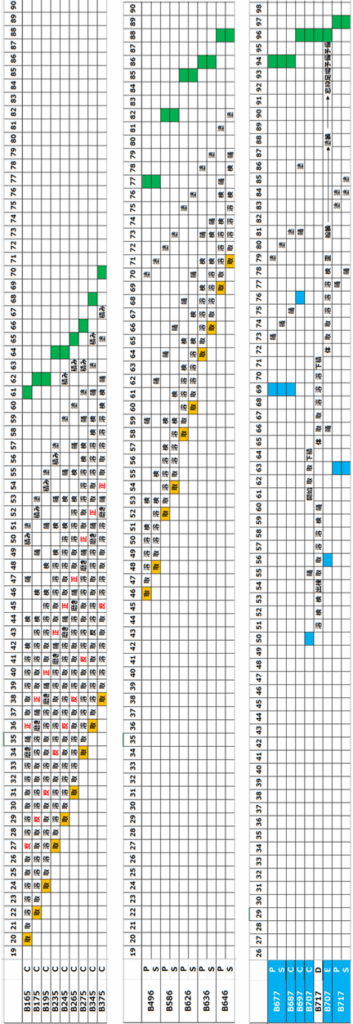
data_BC2={
#-----S01_B522P
"S01_B522P_01":["S01_B522P_01__14Lx13B_Q01",-1,17,99-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[11,15,28,1,15]],0,[13,14,0],182],
"S01_B522P_11":["S01_B522P_11__14Lx13B_B02",-1,4,116-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[9,3,16,2,16]],0,[13,14,0],182],
"S01_B522P_21":["S01_B522P_21__14Lx13B_Q01",-1,2,120-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[11,28,41,1,15]],0,[13,14,0],182],
"S01_B522P_29":["S01_B522P_29__14Lx13B_Q02",-2,2,122-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[12,34,47,1,15]],0,[13,14,0],182],
#
"S01_B522P_00":["S01_B522P_00__14Lx13B_入荷",2,1,99-44,["S01_B522P_01","S01_B522P_02","S01_B522P_03","S01_B522P_04","0"],[[0,-1],[0,-1],[0,-1],[0,-1],[0,0]],[[11,15,28,1,15]],0,[13,14,0],182],
"S01_B522P_10":["S01_B522P_10__14Lx13B_入ブ",6,1,116-44,["S01_B522P_11","S01_B522P_42","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[9,3,16,2,16]],0,[13,14,0],182],
"S01_B522P_20":["S01_B522P_20__14Lx13B_出ブ",7,1,120-44,["S01_B522P_21","S01_B522P_52","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[11,28,41,1,15]],0,[13,14,0],182],
"S01_B522P_99":["S01_B522P_99__14Lx13B_搭載",0,1,124-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,0],
#
"S01_B522P_02":["S01_B522P_02__14Lx13B_溶接",11,0,0,["S01_B522P_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,72],
"S01_B522P_03":["S01_B522P_03__14Lx13B_鉄艤",15,0,0,["S01_B522P_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,7],
"S01_B522P_04":["S01_B522P_04__14Lx13B_甲配",16,0,0,["S01_B522P_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,16],
"S01_B522P_42":["S01_B522P_42__14Lx13B_塗装",18,0,0,["S01_B522P_20","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,90],
"S01_B522P_52":["S01_B522P_52__14Lx13B_鉄艤",15,0,0,["S01_B522P_99","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,3],
#-----S01_B522S
"S01_B522S_01":["S01_B522S_01__14Lx13B_Q01",-1,20,99-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[11,28,41,2,16]],0,[13,14,0],182],
"S01_B522S_11":["S01_B522S_11__14Lx13B_B03",-1,4,119-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[10,3,16,3,17]],0,[13,14,0],182],
"S01_B522S_21":["S01_B522S_21__14Lx13B_R03",-1,1,123-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[27,3,16,4,18]],0,[13,14,0],182],
#
"S01_B522S_00":["S01_B522S_00__14Lx13B_入荷",2,1,99-44,["S01_B522S_01","S01_B522S_02","S01_B522S_03","S01_B522S_04","0"],[[0,-1],[0,-1],[0,-1],[0,-1],[0,0]],[[11,28,41,2,16]],0,[13,14,0],182],
"S01_B522S_10":["S01_B522S_10__14Lx13B_入ブ",6,1,119-44,["S01_B522S_11","S01_B522S_42","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[10,3,16,3,17]],0,[13,14,0],182],
"S01_B522S_20":["S01_B522S_20__14Lx13B_出ブ",7,1,123-44,["S01_B522S_21","S01_B522S_52","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[27,3,16,4,18]],0,[13,14,0],182],
"S01_B522S_99":["S01_B522S_99__14Lx13B_搭載",0,1,124-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,0],
#
"S01_B522S_02":["S01_B522S_02__14Lx13B_溶接",11,1,1,["S01_B522S_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,72],
"S01_B522S_03":["S01_B522S_03__14Lx13B_鉄艤",15,0,0,["S01_B522S_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,7],
"S01_B522S_04":["S01_B522S_04__14Lx13B_甲配",16,0,0,["S01_B522S_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,16],
"S01_B522S_42":["S01_B522S_42__14Lx13B_塗装",18,0,0,["S01_B522S_20","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,90],
"S01_B522S_52":["S01_B522S_52__14Lx13B_鉄艤",15,0,0,["S01_B522S_99","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,3],
#-----U1793_091_4S6P
"S01_B552P_09":["S01_B552P_09__14Lx13B_Q04",-2,4,111-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[14,28,41,1,15]],0,[13,14,0],182],
"S01_B552P_01":["S01_B552P_01__14Lx13B_Q06",-1,5,115-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[16,28,41,1,15]],0,[13,14,0],182],
"S01_B552P_11":["S01_B552P_11__14Lx13B_B02",-1,4,120-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[9,3,16,4,18]],0,[13,14,0],182],
"S01_B552P_21":["S01_B552P_21__14Lx13B_P04",-1,1,124-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[4,13,27,-2,11]],0,[14,13,0],182],
#
"S01_B552P_00":["S01_B552P_00__14Lx13B_入荷",2,1,111-44,["S01_B552P_01","S01_B552P_02","S01_B552P_03","S01_B552P_04","0"],[[0,-1],[0,-1],[0,-1],[0,-1],[0,0]],[[14,28,41,1,15]],0,[13,14,0],182],
"S01_B552P_10":["S01_B552P_10__14Lx13B_入ブ",6,1,120-44,["S01_B552P_11","S01_B552P_42","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[9,3,16,4,18]],0,[13,14,0],182],
"S01_B552P_20":["S01_B552P_20__14Lx13B_出ブ",7,1,124-44,["S01_B552P_21","S01_B552P_52","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[4,13,27,-2,11]],0,[14,13,0],182],
"S01_B552P_99":["S01_B552P_99__14Lx13B_搭載",0,1,125-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,0],
#
"S01_B552P_02":["S01_B552P_02__14Lx13B_溶接",11,0,0,["S01_B552P_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,72],
"S01_B552P_03":["S01_B552P_03__14Lx13B_鉄艤",15,0,0,["S01_B552P_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,10],
"S01_B552P_04":["S01_B552P_04__14Lx13B_甲配",16,0,0,["S01_B552P_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,13],
"S01_B552P_42":["S01_B552P_42__14Lx13B_塗装",18,0,0,["S01_B552P_20","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,90],
"S01_B552P_52":["S01_B552P_52__14Lx13B_鉄艤",15,0,0,["S01_B552P_99","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,5],
#-----S01_B552S
"S01_B552S_09":["S01_B552S_09__14Lx13B_Q04",-2,3,112-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[14,15,28,1,15]],0,[13,14,0],182],
"S01_B552S_01":["S01_B552S_01__14Lx13B_Q06",-1,6,115-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[16,15-1,28-1,1,15]],0,[13,14,0],182],
"S01_B552S_11":["S01_B552S_11__14Lx13B_B01",-1,4,121-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[8,3,16,4,18]],0,[13,14,0],182],
#
"S01_B552S_00":["S01_B552S_00__14Lx13B_入荷",2,1,112-44,["S01_B552S_01","S01_B552S_02","S01_B552S_03","S01_B552S_04","0"],[[0,-1],[0,-1],[0,-1],[0,-1],[0,0]],[[14,15,28,1,15]],0,[13,14,0],182],
"S01_B552S_10":["S01_B552S_10__14Lx13B_入ブ",6,1,121-44,["S01_B552S_11","S01_B552S_42","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[8,3,16,4,18]],0,[13,14,0],182],
#"S01_B552S_20":["S01_B552S_20__14Lx13B_出ブ",7,1,125-44,["S01_B552S_21","S01_B552S_52","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[22,0,13,0,14]],0,[13,14,0],182],
"S01_B552S_99":["S01_B552S_99__14Lx13B_搭載",0,1,125-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,0],
#
"S01_B552S_02":["S01_B552S_02__14Lx13B_溶接",11,0,0,["S01_B552S_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,72],
"S01_B552S_03":["S01_B552S_03__14Lx13B_鉄艤",15,0,0,["S01_B552S_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,10],
"S01_B552S_04":["S01_B552S_04__14Lx13B_甲配",16,0,0,["S01_B552S_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,13],
"S01_B552S_42":["S01_B552S_42__14Lx13B_塗装",18,0,0,["S01_B552S_52","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,90],
"S01_B552S_52":["S01_B552S_52__14Lx13B_鉄艤",16,0,0,["S01_B552S_99","0","0","0","0"],[[0,-1],[0,0],[0,0],[0,0],[0,0]],0,0,1,5],
#-----S01_B602P
"S01_B602P_09":["S01_B602P_09__14Lx13B_Q04",-2,3,112-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[14,1,14,1,15]],0,[13,14,0],182],
"S01_B602P_01":["S01_B602P_01__14Lx13B_Q06",-1,8,115-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[16,1,14,2,16]],0,[13,14,0],182],
"S01_B602P_11":["S01_B602P_11__14Lx13B_B03",-1,6,123-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[10,2,15,3,17]],0,[13,14,0],182],
#
"S01_B602P_00":["S01_B602P_00__14Lx13B_入荷",2,1,112-44,["S01_B602P_01","S01_B602P_02","S01_B602P_03","S01_B602P_04","0"],[[0,-1],[0,-1],[0,-1],[0,-1],[0,0]],[[14,1,14,1,15]],0,[13,14,0],182],
"S01_B602P_10":["S01_B602P_10__14Lx13B_入ブ",6,1,123-44,["S01_B602P_11","S01_B602P_42","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[10,2,15,3,17]],0,[13,14,0],182],
#"S01_B602P_20":["S01_B602P_20__14Lx13B_出ブ",7,1,129-44,["S01_B602P_21","S01_B602P_52","0","0","0"],[[0,-1],[0,0],[0,0],[0,0],[0,0]],[[10,2,15,3,17]],0,[13,14,0],182],
"S01_B602P_99":["S01_B602P_99__14Lx13B_搭載",0,1,129-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,0],
#
"S01_B602P_02":["S01_B602P_02__14Lx13B_溶接",11,0,0,["S01_B602P_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,72],
"S01_B602P_03":["S01_B602P_03__14Lx13B_鉄艤",15,0,0,["S01_B602P_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,13],
"S01_B602P_04":["S01_B602P_04__14Lx13B_甲配",16,0,0,["S01_B602P_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,13],
"S01_B602P_42":["S01_B602P_42__14Lx13B_塗装",18,0,0,["S01_B602P_52","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,90],
"S01_B602P_52":["S01_B602P_52__14Lx13B_鉄艤",15,0,0,["S01_B602P_99","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,5],
#-----S01_B602S: #"S01_B602S_21"
"S01_B602S_01":["S01_B602S_01__14Lx13B_Q01",-1,9,112-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[11,1,14,1,15]],0,[13,14,0],182],
"S01_B602S_09":["S01_B602S_09__14Lx13B_Q01",-2,3,121-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[11,2,15,1,15]],0,[13,14,0],182],
"S01_B602S_11":["S01_B602S_11__14Lx13B_B02",-1,3,124-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[9,3,16,3,17]],0,[13,14,0],182],
"S01_B602S_21":["S01_B602S_21__14Lx13B_Q02",-1,1,127-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[12,27,40,2,16]],0,[13,14,0],182],
#
"S01_B602S_00":["S01_B602S_00__14Lx13B_入荷",2,1,112-44,["S01_B602S_01","S01_B602S_02","S01_B602S_03","S01_B602S_04","0"],[[0,-1],[0,-1],[0,-1],[0,-1],[0,0]],[[11,1,14,1,15]],0,[13,14,0],182],
"S01_B602S_10":["S01_B602S_10__14Lx13B_入ブ",6,1,124-44,["S01_B602S_11","S01_B602S_42","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[9,3,16,3,17]],0,[13,14,0],182],
"S01_B602S_20":["S01_B602S_20__14Lx13B_出ブ",7,1,127-44,["S01_B602S_21","S01_B602S_52","0","0","0"],[[0,-1],[0,-1],[0,-1],[0,0],[0,0]],[[12,27,40,2,16]],0,[13,14,0],182],
"S01_B602S_99":["S01_B602S_99__14Lx13B_搭載",0,1,128-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,0],
#
"S01_B602S_02":["S01_B602S_02__14Lx13B_溶接",11,0,0,["S01_B602S_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,72],
"S01_B602S_03":["S01_B602S_03__14Lx13B_鉄艤",15,0,0,["S01_B602S_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,13],
"S01_B602S_04":["S01_B602S_04__14Lx13B_甲配",16,0,0,["S01_B602S_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,13],
"S01_B602S_42":["S01_B602S_42__14Lx13B_塗装",18,0,0,["S01_B602S_20","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,90],
"S01_B602S_52":["S01_B602S_52__14Lx13B_鉄艤",15,0,0,["S01_B602S_99","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,5],
#-----S01_B392P #"S01_B392P_31"
"S01_B392P_01":["S01_B392P_01__12Lx14B_P01",-1,14,75-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[1,47,59,-1,13]],0,[12,14,0],168],
"S01_B392P_11":["S01_B392P_11__12Lx14B_P04",-1,4,89-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[4,15,27,31,45]],0,[12,14,0],168],
"S01_B392P_21":["S01_B392P_21__12Lx14B_P04",-1,4,93-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[4,1,13,16,30]],0,[12,14,0],168],
"S01_B392P_31":["S01_B392P_31__12Lx14B_Q02",-1,3,97-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[12,39+1,51+1,1,15]],0,[12,14,0],168],
"S01_B392P_41":["S01_B392P_41__12Lx14B_B01",-1,4,100-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[8,3,15,4,18]],0,[12,14,0],168],
"S01_B392P_59":["S01_B392P_59__12Lx14B_R03",-2,1,104-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[27,2,14,4,18]],0,[12,14,0],168],
"S01_B392P_51":["S01_B392P_51__12Lx14B_P03",-1,9,105-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[3,3,15,2,16]],0,[12,14,0],168],
#
"S01_B392P_00":["S01_B392P_00__12Lx14B_開始",1,1,75-44,["S01_B392P_01","S01_B392P_02","S01_B392P_05","0","0"],[[0,-1],[0,-1],[0,-1],[0,0],[0,0]],[[1,47,59,-1,13]],0,[12,14,0],168],
"S01_B392P_10":["S01_B392P_10__12Lx14B_反転",4,1,89-44,["S01_B392P_11","S01_B392P_12","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[4,15,27,31,45]],0,[12,14,0],168],
"S01_B392P_20":["S01_B392P_20__12Lx14B_正転",3,1,93-44,["S01_B392P_21","S01_B392P_22","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[4,1,13,16,30]],0,[12,14,0],168],
"S01_B392P_30":["S01_B392P_30__12Lx14B_出棟",5,1,97-44,["S01_B392P_31","S01_B392P_32","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[12,39,51,1,15]],0,[12,14,0],168],
"S01_B392P_40":["S01_B392P_40__12Lx14B_入ブ",6,1,100-44,["S01_B392P_41","S01_B392P_42","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[8,3,15,4,18]],0,[12,14,0],168],
"S01_B392P_50":["S01_B392P_50__12Lx14B_出ブ",7,1,104-44,["S01_B392P_51","S01_B392P_52","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[3,3,15,2,16]],0,[12,14,0],168],
"S01_B392P_99":["S01_B392P_99__12Lx14B_搭載",0,1,114-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,0],
#
"S01_B392P_02":["S01_B392P_02__12Lx14B_取付",10,0,0,["S01_B392P_03","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38*4],
"S01_B392P_03":["S01_B392P_03__12Lx14B_溶接",11,0,0,["S01_B392P_04","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,64*3],
"S01_B392P_04":["S01_B392P_04__12Lx14B_取付",12,0,0,["S01_B392P_05","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38*2],
"S01_B392P_05":["S01_B392P_05__12Lx14B_溶接",13,0,0,["S01_B392P_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,38],
"S01_B392P_12":["S01_B392P_12__12Lx14B_溶接",11,0,0,["S01_B392P_13","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,64*3],
"S01_B392P_13":["S01_B392P_13__12Lx14B_検査",14,1,0,["S01_B392P_20","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,0],
"S01_B392P_22":["S01_B392P_22__12Lx14B_溶接",11,0,0,["S01_B392P_23","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,30*3],
"S01_B392P_23":["S01_B392P_23__12Lx14B_鉄艤",15,0,0,["S01_B392P_30","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,10],
"S01_B392P_32":["S01_B392P_32__12Lx14B_検査",14,2,0,["S01_B392P_33","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,0],
"S01_B392P_33":["S01_B392P_33__12Lx14B_甲配",16,0,0,["S01_B392P_40","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,4],
"S01_B392P_42":["S01_B392P_42__12Lx14B_塗装",18,0,0,["S01_B392P_50","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,90],
"S01_B392P_52":["S01_B392P_52__12Lx14B_鉄艤",15,0,0,["S01_B392P_99","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,5],
#-----S01_B392S
"S01_B392S_01":["S01_B392S_01__12Lx14B_P01",-1,12,78-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[1,35,47,1,15]],0,[12,14,0],168],
"S01_B392S_09":["S01_B392S_09__12Lx14B_R03",-2,2,90-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[27,4,16,4,18]],0,[12,14,0],168],
"S01_B392S_11":["S01_B392S_11__12Lx14B_P04",-1,3,92-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[4,1,15,33,45]],0,[14,12,0],168],
"S01_B392S_21":["S01_B392S_21__12Lx14B_P04",-1,6,95-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[4,-1,11,31,45]],0,[12,14,0],168],
"S01_B392S_31":["S01_B392S_31__12Lx14B_Q02",-1,3,101-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[12,40,52,1,15]],0,[12,14,0],168],
"S01_B392S_41":["S01_B392S_41__12Lx14B_B03",-1,4,104-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[10,3,15,3,17]],0,[12,14,0],168],
"S01_B392S_59":["S01_B392S_59__12Lx14B_R03",-2,1,108-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[27,4,16,3,17]],0,[12,14,0],168],
"S01_B392S_51":["S01_B392S_51__12Lx14B_P03",-1,5,109-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[3,14+1,26+1,2,16]],0,[12,14,0],168],
#
"S01_B392S_00":["S01_B392S_00__12Lx14B_開始",1,1,78-44,["S01_B392S_01","S01_B392S_02","S01_B392S_05","0","0"],[[0,-1],[0,-1],[0,-1],[0,0],[0,0]],[[1,35,47,1,15]],0,[12,14,0],168],
"S01_B392S_10":["S01_B392S_10__12Lx14B_反転",4,1,92-44,["S01_B392S_11","S01_B392S_12","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[4,1,15,33,45]],0,[14,12,0],168],
"S01_B392S_20":["S01_B392S_20__12Lx14B_正転",3,1,95-44,["S01_B392S_21","S01_B392S_22","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[4,-1,11,31,45]],0,[12,14,0],168],
"S01_B392S_30":["S01_B392S_30__12Lx14B_出棟",5,1,101-44,["S01_B392S_31","S01_B392S_32","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[12,40,52,1,15]],0,[12,14,0],168],
"S01_B392S_40":["S01_B392S_40__12Lx14B_入ブ",6,1,104-44,["S01_B392S_41","S01_B392S_42","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[10,3,15,3,17]],0,[12,14,0],168],
"S01_B392S_50":["S01_B392S_50__12Lx14B_出ブ",7,1,108-44,["S01_B392S_51","S01_B392S_52","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[3,14+1,26+1,2,16]],0,[12,14,0],168],
"S01_B392S_99":["S01_B392S_99__12Lx14B_搭載",0,1,114-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,0],
#
"S01_B392S_02":["S01_B392S_02__12Lx14B_取付",10,0,0,["S01_B392S_03","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38*4],
"S01_B392S_03":["S01_B392S_03__12Lx14B_溶接",11,0,0,["S01_B392S_04","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,64*3],
"S01_B392S_04":["S01_B392S_04__12Lx14B_取付",12,0,0,["S01_B392S_05","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38*1],
"S01_B392S_05":["S01_B392S_05__12Lx14B_溶接",13,0,0,["S01_B392S_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,38],
"S01_B392S_12":["S01_B392S_12__12Lx14B_溶接",11,0,0,["S01_B392S_13","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,64*3],
"S01_B392S_13":["S01_B392S_13__12Lx14B_検査",14,1,0,["S01_B392S_20","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,0],
"S01_B392S_22":["S01_B392S_22__12Lx14B_溶接",11,0,0,["S01_B392S_23","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,30*3],
"S01_B392S_23":["S01_B392S_23__12Lx14B_鉄艤",15,0,0,["S01_B392S_30","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,10],
"S01_B392S_32":["S01_B392S_32__12Lx14B_検査",14,2,0,["S01_B392S_33","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,0],
"S01_B392S_33":["S01_B392S_33__12Lx14B_甲配",16,0,0,["S01_B392S_40","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,4],
"S01_B392S_42":["S01_B392S_42__12Lx14B_塗装",18,0,0,["S01_B392S_50","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,90],
"S01_B392S_52":["S01_B392S_52__12Lx14B_鉄艤",15,0,0,["S01_B392S_99","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,5],
#-----S01_B422P
"S01_B422P_01":["S01_B422P_01__5Lx13B_P05",-1,11,79-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[5,38,51,1,6]],0,[13,5,0],65],
"S01_B422P_11":["S01_B422P_11__5Lx13B_P07",-1,4,90-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[7,2,15,9,14]],0,[13,5,0],65],
"S01_B422P_21":["S01_B422P_21__5Lx13B_P07",-1,14,94-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[7,52,57,17,30]],0,[5,13,0],65],
"S01_B422P_31":["S01_B422P_31__5Lx13B_Q05",-1,1,108-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[15,20,25,2,15]],0,[5,13,0],65],
"S01_B422P_41":["S01_B422P_41__5Lx13B_B02",-1,4,109-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[9,10,15,3,16]],0,[5,13,0],65],
"S01_B422P_51":["S01_B422P_51__5Lx13B_Q03",-1,2,113-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[13,1,14,13,18]],0,[13,5,0],65],
"S01_B422P_59":["S01_B422P_59__5Lx13B_Q05",-2,2,115-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[15,13,26,1,6]],0,[13,5,0],65],
#
"S01_B422P_00":["S01_B422P_00__5Lx13B_開始",1,1,79-44,["S01_B422P_01","S01_B422P_02","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[5,38,51,1,6]],0,[13,5,0],65],
"S01_B422P_10":["S01_B422P_10__5Lx13B_反転",4,1,90-44,["S01_B422P_11","S01_B422P_12","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[7,2,15,9,14]],0,[13,5,0],65],
"S01_B422P_20":["S01_B422P_20__5Lx13B_正転",3,1,94-44,["S01_B422P_21","S01_B422P_22","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[7,52,57,17,30]],0,[5,13,0],65],
"S01_B422P_30":["S01_B422P_30__5Lx13B_出棟",5,1,108-44,["S01_B422P_31","S01_B422P_32","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[15,20,25,2,15]],0,[5,13,0],65],
"S01_B422P_40":["S01_B422P_40__5Lx13B_入ブ",6,1,109-44,["S01_B422P_41","S01_B422P_42","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[9,10,15,3,16]],0,[5,13,0],65],
"S01_B422P_50":["S01_B422P_50__5Lx13B_出ブ",7,1,113-44,["S01_B422P_51","S01_B422P_52","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[13,1,14,13,18]],0,[13,5,0],65],
"S01_B422P_99":["S01_B422P_99__5Lx13B_搭載",0,1,117-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,0],
#
"S01_B422P_02":["S01_B422P_02__5Lx13B_取付",10,0,0,["S01_B422P_03","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,21*3],
"S01_B422P_03":["S01_B422P_03__5Lx13B_取付",12,0,0,["S01_B422P_04","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,21*2],
"S01_B422P_04":["S01_B422P_04__5Lx13B_溶接",11,0,0,["S01_B422P_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,29*3],
"S01_B422P_12":["S01_B422P_12__5Lx13B_溶接",11,0,0,["S01_B422P_20","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,29*3],
"S01_B422P_22":["S01_B422P_22__5Lx13B_溶接",11,0,0,["S01_B422P_23","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,21*2],
"S01_B422P_23":["S01_B422P_23__5Lx13B_検査",14,2,0,["S01_B422P_24","S01_B422P_25","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,0],
"S01_B422P_24":["S01_B422P_24__5Lx13B_甲配",16,0,0,["S01_B422P_30","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,4],
"S01_B422P_25":["S01_B422P_25__5Lx13B_鉄艤",15,0,0,["S01_B422P_30","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,3],
"S01_B422P_32":["S01_B422P_32__5Lx13B_予備",14,1,0,["S01_B422P_40","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,0],
"S01_B422P_42":["S01_B422P_42__5Lx13B_塗装",18,0,0,["S01_B422P_50","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,40],
"S01_B422P_52":["S01_B422P_52__5Lx13B_予備",14,1,0,["S01_B422P_99","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,0],
#-----S01_B422S "S01_B422S_21
"S01_B422S_01":["S01_B422S_01__5Lx13B_P05",-1,11,79-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[5,39,52,5+1,10+1]],0,[13,5,0],65],
"S01_B422S_11":["S01_B422S_11__5Lx13B_P07",-1,4,90-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[7,57,62,17,30]],0,[5,13,0],65],
"S01_B422S_21":["S01_B422S_21__5Lx13B_P07",-1,14,94-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[7,57,62,17,30]],0,[5,13,0],65],
"S01_B422S_31":["S01_B422S_31__5Lx13B_Q05",-1,1,108-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[15,15,20,2,15]],0,[5,13,0],65],
"S01_B422S_41":["S01_B422S_41__5Lx13B_B02",-1,4,109-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[9,5,10,3,16]],0,[5,13,0],65],
"S01_B422S_51":["S01_B422S_51__5Lx13B_Q03",-1,2,113-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[13,1,14,18,23]],0,[13,5,0],65],
"S01_B422S_59":["S01_B422S_59__5Lx13B_Q05",-2,2,115-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[15,-2,11,1,6]],0,[13,5,0],65],
#
"S01_B422S_00":["S01_B422S_00__5Lx13B_開始",1,1,79-44,["S01_B422S_01","S01_B422S_02","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[5,38,51,5+1,10+1]],0,[13,5,0],65],
"S01_B422S_10":["S01_B422S_10__5Lx13B_反転",4,1,90-44,["S01_B422S_11","S01_B422S_12","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[7,57,62,17,30]],0,[5,13,0],65],
"S01_B422S_20":["S01_B422S_20__5Lx13B_正転",3,1,94-44,["S01_B422S_21","S01_B422S_22","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[7,57,62,17,30]],0,[5,13,0],65],
"S01_B422S_30":["S01_B422S_30__5Lx13B_出棟",5,1,108-44,["S01_B422S_31","S01_B422S_32","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[15,15,20,2,15]],0,[5,13,0],65],
"S01_B422S_40":["S01_B422S_40__5Lx13B_入ブ",6,1,109-44,["S01_B422S_41","S01_B422S_42","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[9,5,10,3,16]],0,[5,13,0],65],
"S01_B422S_50":["S01_B422S_50__5Lx13B_出ブ",7,1,113-44,["S01_B422S_51","S01_B422S_52","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[13,1,14,18,23]],0,[13,5,0],65],
"S01_B422S_99":["S01_B422S_99__5Lx13B_搭載",0,1,117-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,0],
#
"S01_B422S_02":["S01_B422S_02__5Lx13B_取付",10,0,0,["S01_B422S_03","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,21*3],
"S01_B422S_03":["S01_B422S_03__5Lx13B_取付",12,0,0,["S01_B422S_04","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,21*2],
"S01_B422S_04":["S01_B422S_04__5Lx13B_溶接",11,0,0,["S01_B422S_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,29*3],
"S01_B422S_12":["S01_B422S_12__5Lx13B_溶接",11,0,0,["S01_B422S_20","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,29*3],
"S01_B422S_22":["S01_B422S_22__5Lx13B_溶接",11,0,0,["S01_B422S_23","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,21*2],
"S01_B422S_23":["S01_B422S_23__5Lx13B_検査",14,2,0,["S01_B422S_24","S01_B422S_25","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,0],
"S01_B422S_24":["S01_B422S_24__5Lx13B_甲配",16,0,0,["S01_B422S_30","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,4],
"S01_B422S_25":["S01_B422S_25__5Lx13B_鉄艤",15,0,0,["S01_B422S_30","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,3],
"S01_B422S_32":["S01_B422S_32__5Lx13B_予備",14,1,0,["S01_B422S_40","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,0],
"S01_B422S_42":["S01_B422S_42__5Lx13B_塗装",18,0,0,["S01_B422S_50","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,40],
"S01_B422S_52":["S01_B422S_52__5Lx13B_予備",14,1,0,["S01_B422S_99","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,0],
#-----S01_B432S
"S01_B432S_01":["S01_B432S_01__10Lx13B_P02",-1,10,83-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[2,46,56,1,14]],0,[10,13,0],130],
"S01_B432S_09":["S01_B432S_09__10Lx13B_R03",-2,1,93-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[27,6,16,4,17]],0,[10,13,0],130],
"S01_B432S_11":["S01_B432S_11__10Lx13B_P04",-1,5,94-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[4,14,27,16,26]],0,[13,10,0],130],
"S01_B432S_21":["S01_B432S_21__10Lx13B_P04",-1,4,99-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[4,14,27,16,26]],0,[13,10,0],130],
"S01_B432S_31":["S01_B432S_31__10Lx13B_Q02",-1,2,103-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[12,26,39,2,12]],0,[13,10,0],130],
"S01_B432S_41":["S01_B432S_41__10Lx13B_B02",-1,4,105-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[9,3,16,6,16]],0,[13,10,0],130],
"S01_B432S_51":["S01_B432S_51__10Lx13B_Q02",-1,7,109-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[12,40,50,2,15]],0,[10,13,0],130],
#
"S01_B432S_00":["S01_B432S_00__10Lx13B_開始",1,1,83-44,["S01_B432S_01","S01_B432S_02","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[2,46,56,1,14]],0,[10,13,0],130],
"S01_B432S_10":["S01_B432S_10__10Lx13B_反転",4,1,94-44,["S01_B432S_11","S01_B432S_12","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[4,14,27,16,26]],0,[13,10,0],130],
"S01_B432S_20":["S01_B432S_20__10Lx13B_正転",3,1,99-44,["S01_B432S_21","S01_B432S_22","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[4,14,27,16,26]],0,[13,10,0],130],
"S01_B432S_30":["S01_B432S_30__10Lx13B_出棟",5,1,103-44,["S01_B432S_31","S01_B432S_32","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[12,26,39,2,12]],0,[13,10,0],130],
"S01_B432S_40":["S01_B432S_40__10Lx13B_入ブ",6,1,105-44,["S01_B432S_41","S01_B432S_42","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[9,3,16,6,16]],0,[13,10,0],130],
"S01_B432S_50":["S01_B432S_50__10Lx13B_出ブ",7,1,109-44,["S01_B432S_51","S01_B432S_52","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[12,40,50,2,15]],0,[10,13,0],130],
"S01_B432S_99":["S01_B432S_99__10Lx13B_搭載",0,1,116-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,0],
#
"S01_B432S_02":["S01_B432S_02__10Lx13B_取付",10,0,0,["S01_B432S_03","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38*4],
"S01_B432S_03":["S01_B432S_03__10Lx13B_溶接",11,0,0,["S01_B432S_04","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,64*3],
"S01_B432S_04":["S01_B432S_04__10Lx13B_取付",12,0,0,["S01_B432S_05","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38*2],
"S01_B432S_05":["S01_B432S_05__10Lx13B_溶接",13,0,0,["S01_B432S_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,38],
"S01_B432S_12":["S01_B432S_12__10Lx13B_溶接",11,0,0,["S01_B432S_13","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,64*3],
"S01_B432S_13":["S01_B432S_13__10Lx13B_検査",14,1,0,["S01_B432S_20","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,0],
"S01_B432S_22":["S01_B432S_22__10Lx13B_溶接",11,0,0,["S01_B432S_23","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38],
"S01_B432S_23":["S01_B432S_23__10Lx13B_取付",10,0,0,["S01_B432S_24","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,29],
"S01_B432S_24":["S01_B432S_24__10Lx13B_溶接",11,0,0,["S01_B432S_25","S01_B432S_26","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38*2],
"S01_B432S_25":["S01_B432S_25__10Lx13B_甲配",16,0,0,["S01_B432S_30","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,9],
"S01_B432S_26":["S01_B432S_26__10Lx13B_鉄艤",15,0,0,["S01_B432S_30","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,13],
"S01_B432S_32":["S01_B432S_32__10Lx13B_検査",14,2,0,["S01_B432S_40","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,0],
"S01_B432S_42":["S01_B432S_42__10Lx13B_塗装",18,0,0,["S01_B432S_50","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,90],
"S01_B432S_52":["S01_B432S_52__10Lx13B_鉄艤",15,0,0,["S01_B432S_99","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,6],
#-----S01_B432P
"S01_B432P_01":["S01_B432P_01__10Lx13B_P02",-1,11,83-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[2,34,44,1,14]],0,[10,13,0],130],
"S01_B432P_08":["S01_B432P_09__10Lx13B_R02",-2,1,94-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[26,3,13,1,14]],0,[10,13,0],130],
"S01_B432P_09":["S01_B432P_11__10Lx13B_R03",-2,2,95-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[27,5,15,3,16]],0,[10,13,0],130],
"S01_B432P_11":["S01_B432P_11__10Lx13B_P04",-1,4,97-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[4,16,26,32,45]],0,[10,13,0],130],
"S01_B432P_21":["S01_B432P_21__10Lx13B_P04",-1,5,101-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[4,16,26,32,45]],0,[10,13,0],130],
"S01_B432P_31":["S01_B432P_31__10Lx13B_Q02",-1,2,106-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[12,32,42,1,14]],0,[10,13,0],130],
"S01_B432P_41":["S01_B432P_41__10Lx13B_B03",-1,4,108-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[10,5,15,4,17]],0,[10,13,0],130],
"S01_B432P_51":["S01_B432P_51__10Lx13B_Q02",-1,4,112-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[12,29,39,2,15]],0,[10,13,0],130],
#
"S01_B432P_00":["S01_B432P_00__10Lx13B_開始",1,1,83-44,["S01_B432P_01","S01_B432P_02","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[2,34,44,1,14]],0,[10,13,0],130],
"S01_B432P_10":["S01_B432P_10__10Lx13B_反転",4,1,97-44,["S01_B432P_11","S01_B432P_12","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[4,16,26,32,45]],0,[10,13,0],130],
"S01_B432P_20":["S01_B432P_20__10Lx13B_正転",3,1,101-44,["S01_B432P_21","S01_B432P_22","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[4,16,26,32,45]],0,[10,13,0],130],
"S01_B432P_30":["S01_B432P_30__10Lx13B_出棟",5,1,106-44,["S01_B432P_31","S01_B432P_32","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[12,32,42,1,14]],0,[10,13,0],130],
"S01_B432P_40":["S01_B432P_40__10Lx13B_入ブ",6,1,108-44,["S01_B432P_41","S01_B432P_42","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[10,5,15,4,17]],0,[10,13,0],130],
"S01_B432P_50":["S01_B432P_50__10Lx13B_出ブ",7,1,112-44,["S01_B432P_51","S01_B432P_52","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[12,29,39,2,15]],0,[10,13,0],130],
"S01_B432P_99":["S01_B432P_99__10Lx13B_搭載",0,1,116-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,130],
#
"S01_B432P_02":["S01_B432P_02__10Lx13B_取付",10,0,0,["S01_B432P_03","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38*4],
"S01_B432P_03":["S01_B432P_03__10Lx13B_溶接",11,0,0,["S01_B432P_04","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,64*3],
"S01_B432P_04":["S01_B432P_04__10Lx13B_取付",12,0,0,["S01_B432P_05","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38*2],
"S01_B432P_05":["S01_B432P_05__10Lx13B_溶接",13,0,0,["S01_B432P_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,38],
"S01_B432P_12":["S01_B432P_12__10Lx13B_溶接",11,0,0,["S01_B432P_13","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,64*3],
"S01_B432P_13":["S01_B432P_13__10Lx13B_検査",14,1,0,["S01_B432P_20","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,0],
"S01_B432P_22":["S01_B432P_22__10Lx13B_溶接",11,0,0,["S01_B432P_23","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38],
"S01_B432P_23":["S01_B432P_23__10Lx13B_取付",10,0,0,["S01_B432P_24","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,29],
"S01_B432P_24":["S01_B432P_24__10Lx13B_溶接",11,0,0,["S01_B432P_25","S01_B432P_26","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38*2],
"S01_B432P_25":["S01_B432P_25__10Lx13B_甲配",16,0,0,["S01_B432P_30","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,9],
"S01_B432P_26":["S01_B432P_26__10Lx13B_鉄艤",15,0,0,["S01_B432P_30","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,13],
"S01_B432P_32":["S01_B432P_32__10Lx13B_検査",14,2,0,["S01_B432P_40","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,0],
"S01_B432P_42":["S01_B432P_42__10Lx13B_塗装",18,0,0,["S01_B432P_50","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,90],
"S01_B432P_52":["S01_B432P_52__10Lx13B_鉄艤",15,0,0,["S01_B432P_99","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,6],
#-----S01_B462P
"S01_B462P_01":["S01_B462P_01__13Lx9B_P01",-1,14,81-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[1,25,34,0,13]],0,[9,13,0],117],
"S01_B462P_11":["S01_B462P_11__13Lx9B_P03",-1,3,95-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[3,2,15,5,14]],0,[13,9,0],117],
"S01_B462P_21":["S01_B462P_21__13Lx9B_P03",-1,4,98-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[3,1,10,3,16]],0,[9,13,0],117],
"S01_B462P_29":["S01_B462P_29__13Lx9B_R03",-2,1,102-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[26,5,14,4,17]],0,[9,13,0],117],
"S01_B462P_31":["S01_B462P_31__13Lx9B_Q07",-1,7,103-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[17,1,10,0,13]],0,[9,13,0],117],
"S01_B462P_41":["S01_B462P_41__13Lx9B_B01",-1,4,110-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[8,6,15,4,17]],0,[9,13,0],117],
"S01_B462P_51":["S01_B462P_51__13Lx9B_Q09",-1,4,114-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[19,17,26,1,14]],0,[9,13,0],117],
"S01_B462P_59":["S01_B462P_59__13Lx9B_P04",-2,1,118-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[4,17,26,-1,12]],0,[9,13,0],117],
#
"S01_B462P_00":["S01_B462P_00__13Lx9B_開始",1,1,81-44,["S01_B462P_01","S01_B462P_02","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[1,25,34,1,14]],0,[9,13,0],117],
"S01_B462P_10":["S01_B462P_10__13Lx9B_反転",4,1,95-44,["S01_B462P_11","S01_B462P_12","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[3,2,15,5,14]],0,[13,9,0],117],
"S01_B462P_20":["S01_B462P_20__13Lx9B_正転",3,1,98-44,["S01_B462P_21","S01_B462P_22","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[3,1,10,3,16]],0,[9,13,0],117],
"S01_B462P_30":["S01_B462P_30__13Lx9B_出棟",5,1,102-44,["S01_B462P_31","S01_B462P_32","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[17,1,10,-1,12]],0,[9,13,0],117],
"S01_B462P_40":["S01_B462P_40__13Lx9B_入ブ",6,1,110-44,["S01_B462P_41","S01_B462P_42","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[8,6,15,4,17]],0,[9,13,0],117],
"S01_B462P_50":["S01_B462P_50__13Lx9B_出ブ",7,1,114-44,["S01_B462P_51","S01_B462P_52","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[19,17,26,-2,11]],0,[9,13,0],117],
"S01_B462P_99":["S01_B462P_99__13Lx9B_搭載",0,1,119-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,117],
#
"S01_B462P_02":["S01_B462P_02__13Lx9B_取付",10,0,0,["S01_B462P_03","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,30*3],
"S01_B462P_03":["S01_B462P_03__13Lx9B_取付",12,0,0,["S01_B462P_04","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,30*3],
"S01_B462P_04":["S01_B462P_04__13Lx9B_溶接",11,0,0,["S01_B462P_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,39*4],
"S01_B462P_12":["S01_B462P_12__13Lx9B_溶接",11,0,0,["S01_B462P_13","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,39*3],
"S01_B462P_13":["S01_B462P_13__13Lx9B_検査",14,1,0,["S01_B462P_20","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,0],
"S01_B462P_22":["S01_B462P_22__13Lx9B_溶接",11,0,0,["S01_B462P_23","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38],
"S01_B462P_23":["S01_B462P_23__13Lx9B_取付",10,0,0,["S01_B462P_24","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,29],
"S01_B462P_24":["S01_B462P_24__13Lx9B_溶接",11,0,0,["S01_B462P_30","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,38*2],
"S01_B462P_32":["S01_B462P_32__13Lx9B_検査",14,2,0,["S01_B462P_33","S01_B462P_34","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,0],
"S01_B462P_33":["S01_B462P_33__13Lx9B_甲配",16,0,0,["S01_B462P_40","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,13],
"S01_B462P_34":["S01_B462P_34__13Lx9B_鉄艤",15,0,0,["S01_B462P_40","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,12],
"S01_B462P_42":["S01_B462P_42__13Lx9B_塗装",18,0,0,["S01_B462P_50","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,70],
"S01_B462P_52":["S01_B462P_52__13Lx9B_鉄艤",15,0,0,["S01_B462P_99","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,6],
#-----S01_B462S
"S01_B462S_01":["S01_B462S_01__13Lx9B_P01",-1,7,88-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[1,15,24,1,14]],0,[9,13,0],117],
"S01_B462S_09":["S01_B462S_09__13Lx9B_R01",-2,3,95-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[24,2,11,1,14]],0,[9,13,0],117],
"S01_B462S_11":["S01_B462S_11__13Lx9B_P03",-1,7,98-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[3,11,24,5,14]],0,[13,9,0],117],
"S01_B462S_21":["S01_B462S_21__13Lx9B_P03",-1,3,105-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[3,15,24,2,15]],0,[9,13,0],117],
"S01_B462S_29":["S01_B462S_29__13Lx9B_P04",-2,1,108-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[4,-1,12,35,44]],0,[13,9,0],117],
"S01_B462S_31":["S01_B462S_31__13Lx9B_Q05",-1,3,109-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[15,14,23,3,16]],0,[9,13,0],117],
"S01_B462S_41":["S01_B462S_41__13Lx9B_B03",-1,3,112-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[10,4,13,3,16]],0,[9,13,0],117],
"S01_B462S_51":["S01_B462S_51__13Lx9B_Q03",-1,4,115-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[13,38,51,1,10]],0,[13,9,0],117],
#
"S01_B462S_00":["S01_B462S_00__13Lx9B_開始",1,1,88-44,["S01_B462S_01","S01_B462S_02","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[1,15,24,1,14]],0,[9,13,0],117],
"S01_B462S_10":["S01_B462S_10__13Lx9B_反転",4,1,98-44,["S01_B462S_11","S01_B462S_12","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[3,11,24,5,14]],0,[13,9,0],117],
"S01_B462S_20":["S01_B462S_20__13Lx9B_正転",3,1,105-44,["S01_B462S_21","S01_B462S_22","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[3,15,24,3,16]],0,[9,13,0],117],
"S01_B462S_30":["S01_B462S_30__13Lx9B_出棟",5,1,109-44,["S01_B462S_31","S01_B462S_32","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[15,14,23,3,16]],0,[9,13,0],117],
"S01_B462S_40":["S01_B462S_40__13Lx9B_入ブ",6,1,112-44,["S01_B462S_41","S01_B462S_42","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[10,4,13,3,16]],0,[9,13,0],117],
"S01_B462S_50":["S01_B462S_50__13Lx9B_出ブ",7,1,115-44,["S01_B462S_51","S01_B462S_52","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[13,38,51,1,10]],0,[13,9,0],117],
"S01_B462S_99":["S01_B462S_99__13Lx9B_搭載",0,1,119-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,0],
#
"S01_B462S_02":["S01_B462S_02__13Lx9B_取付",10,0,0,["S01_B462S_03","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,30*3],
"S01_B462S_03":["S01_B462S_03__13Lx9B_取付",12,0,0,["S01_B462S_04","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,30*3],
"S01_B462S_04":["S01_B462S_04__13Lx9B_溶接",11,0,0,["S01_B462S_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,39*4],
"S01_B462S_12":["S01_B462S_12__13Lx9B_溶接",11,0,0,["S01_B462S_13","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,39*3],
"S01_B462S_13":["S01_B462S_13__13Lx9B_検査",14,1,0,["S01_B462S_20","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,0],
"S01_B462S_22":["S01_B462S_22__13Lx9B_溶接",11,0,0,["S01_B462S_23","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38],
"S01_B462S_23":["S01_B462S_23__13Lx9B_取付",10,0,0,["S01_B462S_24","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,29],
"S01_B462S_24":["S01_B462S_24__13Lx9B_溶接",11,0,0,["S01_B462S_30","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,38*2],
"S01_B462S_32":["S01_B462S_32__13Lx9B_検査",14,2,0,["S01_B462S_33","S01_B462S_34","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,0],
"S01_B462S_33":["S01_B462S_33__13Lx9B_甲配",16,0,0,["S01_B462S_40","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,13],
"S01_B462S_34":["S01_B462S_34__13Lx9B_鉄艤",15,0,0,["S01_B462S_40","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,12],
"S01_B462S_42":["S01_B462S_42__13Lx9B_塗装",18,0,0,["S01_B462S_50","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,70],
"S01_B462S_52":["S01_B462S_52__13Lx9B_鉄艤",15,0,0,["S01_B462S_99","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,6],
#-----S01_B472P
"S01_B472P_01":["S01_B472P_01__14Lx13B_P01",-1,13,90-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[1,-1,13,1,14]],0,[14,13,0],182],
"S01_B472P_11":["S01_B472P_11__14Lx13B_P04",-1,5,103-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[4,13,27,16,29]],0,[14,13,0],182],
"S01_B472P_21":["S01_B472P_21__14Lx13B_P04",-1,5,108-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[4,13,27,16,29]],0,[14,13,0],182],
"S01_B472P_29":["S01_B472P_29__14Lx13B_R03",-2,1,113-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[27,2,16,4,17]],0,[14,13,0],182],
"S01_B472P_41":["S01_B472P_41__14Lx13B_B01",-1,3,114-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[8,2,15,3,17]],0,[13,14,0],182],
"S01_B472P_51":["S01_B472P_51__14Lx13B_Q02",-1,3,117-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[12,36,49,2,16]],0,[13,14,0],182],
#
"S01_B472P_00":["S01_B472P_00__14Lx13B_開始",1,1,90-44,["S01_B472P_01","S01_B472P_02","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[1,-1,13,1,14]],0,[14,13,0],182],
"S01_B472P_10":["S01_B472P_10__14Lx13B_反転",4,1,103-44,["S01_B472P_11","S01_B472P_12","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[4,13,27,16,29]],0,[14,13,0],182],
"S01_B472P_20":["S01_B472P_20__14Lx13B_正転",3,1,108-44,["S01_B472P_21","S01_B472P_22","0","0","0"],[[0,-1],[0,-1],[0,-1],[0,0],[0,0]],[[4,13,27,16,29]],0,[14,13,0],0],
"S01_B472P_40":["S01_B472P_40__14Lx13B_入ブ",6,1,114-44,["S01_B472P_41","S01_B472P_42","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[8,2,15,3,17]],0,[13,14,0],182],
"S01_B472P_50":["S01_B472P_50__14Lx13B_出ブ",7,1,117-44,["S01_B472P_51","S01_B472P_52","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[12,36,49,2,16]],0,[13,14,0],182],
"S01_B472P_99":["S01_B472P_99__14Lx13B_搭載",0,1,120-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,0],
#
"S01_B472P_02":["S01_B472P_02__13Lx9B_取付",10,0,0,["S01_B472P_03","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38*4],
"S01_B472P_03":["S01_B472P_03__13Lx9B_溶接",11,0,0,["S01_B472P_04","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,64*3],
"S01_B472P_04":["S01_B472P_04__13Lx9B_取付",12,0,0,["S01_B472P_05","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38*2],
"S01_B472P_05":["S01_B472P_05__13Lx9B_溶接",13,0,0,["S01_B472P_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,38],
"S01_B472P_12":["S01_B472P_12__13Lx9B_溶接",11,0,0,["S01_B472P_13","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,64*3],
"S01_B472P_13":["S01_B472P_13__13Lx9B_検査",14,1,0,["S01_B472P_20","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,0],
"S01_B472P_22":["S01_B472P_22__13Lx9B_溶接",11,0,0,["S01_B472P_23","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38],
"S01_B472P_23":["S01_B472P_23__13Lx9B_取付",10,0,0,["S01_B472P_24","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,29],
"S01_B472P_24":["S01_B472P_24__13Lx9B_溶接",11,0,0,["S01_B472P_25","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38*2],
"S01_B472P_25":["S01_B472P_25__13Lx9B_検査",14,2,0,["S01_B472P_26","S01_B472P_27","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,0],
"S01_B472P_26":["S01_B472P_26__13Lx9B_甲配",16,0,0,["S01_B472P_40","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,16],
"S01_B472P_27":["S01_B472P_27__13Lx9B_鉄艤",15,0,0,["S01_B472P_40","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,10],
"S01_B472P_42":["S01_B472P_42__13Lx9B_塗装",18,0,0,["S01_B472P_50","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,90],
"S01_B472P_52":["S01_B472P_52__13Lx9B_鉄艤",15,0,0,["S01_B472P_99","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,5],
#-----S01_B472S
"S01_B472S_01":["S01_B472S_01__14Lx13B_P02",-1,10,90-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[2,15,29,1,14]],0,[14,13,0],182],
"S01_B472S_11":["S01_B472S_11__14Lx13B_P04",-1,5,100-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[4,12,26,-2,11]],0,[14,13,0],182],
"S01_B472S_21":["S01_B472S_21__14Lx13B_P04",-1,7,105-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[4,12,26,-2,11]],0,[14,13,0],182],
"S01_B472S_29":["S01_B472S_29__14Lx13B_Q05",-2,1,112-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[15,1,14,2,16]],0,[13,14,0],182],
"S01_B472S_41":["S01_B472S_41__14Lx13B_B02",-1,3,113-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[9,3,17,3,16]],0,[14,13,0],182],
"S01_B472S_51":["S01_B472S_51__14Lx13B_P04",-1,4,116-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[4,1,15,31,44]],0,[14,13,0],182],
#
"S01_B472S_00":["S01_B472S_00__14Lx13B_開始",1,1,90-44,["S01_B472S_01","S01_B472S_02","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[2,15,29,1,14]],0,[14,13,0],182],
"S01_B472S_10":["S01_B472S_10__14Lx13B_反転",4,1,100-44,["S01_B472S_11","S01_B472S_12","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[4,12,26,-2,11]],0,[14,13,0],182],
"S01_B472S_20":["S01_B472S_20__14Lx13B_正転",3,1,105-44,["S01_B472S_21","S01_B472S_22","0","0","0"],[[0,-1],[0,-1],[0,-1],[0,0],[0,0]],[[4,12,26,-2,11]],0,[14,13,0],182],
"S01_B472S_40":["S01_B472S_40__14Lx13B_入ブ",6,1,113-44,["S01_B472S_41","S01_B472S_42","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[9,3,16,3,17]],0,[13,14,0],182],
"S01_B472S_50":["S01_B472S_50__14Lx13B_出ブ",7,1,116-44,["S01_B472S_51","S01_B472S_52","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[4,1,15,31,44]],0,[14,13,0],182],
"S01_B472S_99":["S01_B472S_99__14Lx13B_搭載",0,1,120-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,0],
#
"S01_B472S_02":["S01_B472S_02__14Lx13B_取付",10,0,0,["S01_B472S_03","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38*4],
"S01_B472S_03":["S01_B472S_03__14Lx13B_溶接",11,0,0,["S01_B472S_04","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,64*3],
"S01_B472S_04":["S01_B472S_04__14Lx13B_取付",12,0,0,["S01_B472S_05","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38*2],
"S01_B472S_05":["S01_B472S_05__14Lx13B_溶接",13,0,0,["S01_B472S_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,38],
"S01_B472S_12":["S01_B472S_12__14Lx13B_溶接",11,0,0,["S01_B472S_13","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,64*3],
"S01_B472S_13":["S01_B472S_13__14Lx13B_検査",14,1,0,["S01_B472S_20","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,0],
"S01_B472S_22":["S01_B472S_22__14Lx13B_溶接",11,0,0,["S01_B472S_23","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38],
"S01_B472S_23":["S01_B472S_23__14Lx13B_取付",10,0,0,["S01_B472S_24","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,29],
"S01_B472S_24":["S01_B472S_24__14Lx13B_溶接",11,0,0,["S01_B472S_25","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38*2],
"S01_B472S_25":["S01_B472S_25__14Lx13B_検査",14,2,0,["S01_B472S_26","S01_B472S_27","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,0],
"S01_B472S_26":["S01_B472S_26__14Lx13B_甲配",16,0,0,["S01_B472S_40","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,16],
"S01_B472S_27":["S01_B472S_27__14Lx13B_鉄艤",15,0,0,["S01_B472S_40","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,10],
"S01_B472S_42":["S01_B472S_42__14Lx13B_塗装",18,0,0,["S01_B472S_50","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,90],
"S01_B472S_52":["S01_B472S_52__14Lx13B_塗装",19,0,0,["S01_B472S_99","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,5],
#-----S01_B502P
"S01_B502P_01":["S01_B502P_01__14Lx13B_P02",-1,11,95-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[2,45,59,1,14]],0,[14,13,0],182],
"S01_B502P_11":["S01_B502P_11__14Lx13B_P04",-1,4,106-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[4,13,27,32,45]],0,[14,13,0],182],
"S01_B502P_21":["S01_B502P_21__14Lx13B_P04",-1,5,110-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[4,13,27,32,45]],0,[14,13,0],182],
"S01_B502P_41":["S01_B502P_41__14Lx13B_B03",-1,4,115-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[10,2,15,3,17]],0,[13,14,0],182],
"S01_B502P_59":["S01_B502P_59__14Lx13B_Q01",-2,1,119-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[11,14,27,1,15]],0,[13,14,0],182],
"S01_B502P_51":["S01_B502P_51__14Lx13B_P04",-1,2,120-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[4,13,27,-2,10]],0,[14,13,0],182],
#
"S01_B502P_00":["S01_B502P_00__14Lx13B_開始",1,1,95-44,["S01_B502P_01","S01_B502P_02","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[2,45,59,1,14]],0,[14,13,0],182],
"S01_B502P_10":["S01_B502P_10__14Lx13B_反転",4,1,106-44,["S01_B502P_11","S01_B502P_12","0","0","0"],[[0,-1],[0,-1],[0,-1],[0,0],[0,0]],[[4,13,27,32,45]],0,[14,13,0],182],
"S01_B502P_20":["S01_B502P_20__14Lx13B_正転",3,1,110-44,["S01_B502P_21","S01_B502P_22","0","0","0"],[[0,-1],[0,-1],[0,-1],[0,0],[0,0]],[[4,13,27,32,45]],0,[14,13,0],182],
"S01_B502P_40":["S01_B502P_40__14Lx13B_入ブ",6,1,115-44,["S01_B502P_41","S01_B502P_42","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[10,2,15,3,17]],0,[13,14,0],182],
"S01_B502P_50":["S01_B502P_50__14Lx13B_出ブ",7,1,119-44,["S01_B502P_51","S01_B502P_52","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[4,13,27,-2,11]],0,[14,13,0],182],
"S01_B502P_99":["S01_B502P_99__14Lx13B_搭載",0,1,122-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,0],
#
"S01_B502P_02":["S01_B502P_02__14Lx13B_取付",10,0,0,["S01_B502P_03","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38*3],
"S01_B502P_03":["S01_B502P_03__14Lx13B_溶接",11,0,0,["S01_B502P_04","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,64*3],
"S01_B502P_04":["S01_B502P_04__14Lx13B_取付",12,0,0,["S01_B502P_05","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38*2],
"S01_B502P_05":["S01_B502P_05__14Lx13B_溶接",13,0,0,["S01_B502P_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,38],
"S01_B502P_12":["S01_B502P_12__14Lx13B_溶接",11,0,0,["S01_B502P_13","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,64*3],
"S01_B502P_13":["S01_B502P_13__14Lx13B_検査",14,1,0,["S01_B502P_20","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,0],
"S01_B502P_22":["S01_B502P_22__14Lx13B_溶接",11,0,0,["S01_B502P_23","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38],
"S01_B502P_23":["S01_B502P_23__14Lx13B_取付",10,0,0,["S01_B502P_24","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,29],
"S01_B502P_24":["S01_B502P_24__14Lx13B_溶接",11,0,0,["S01_B502P_25","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38*2],
"S01_B502P_25":["S01_B502P_25__14Lx13B_検査",14,1,0,["S01_B502P_26","S01_B502P_27","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,0],
"S01_B502P_26":["S01_B502P_26__14Lx13B_甲配",16,0,0,["S01_B502P_40","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,10],
"S01_B502P_27":["S01_B502P_27__14Lx13B_鉄艤",15,0,0,["S01_B502P_40","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,16],
"S01_B502P_42":["S01_B502P_42__14Lx13B_塗装",18,0,0,["S01_B502P_50","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,90],
"S01_B502P_52":["S01_B502P_52__14Lx13B_鉄艤",15,0,0,["S01_B502P_99","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,5],
#-----S01_B502S
"S01_B502S_01":["S01_B502S_01__14Lx13B_P02",-1,14,95-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[2,31,45,1,14]],0,[14,13,0],182],
"S01_B502S_11":["S01_B502S_11__14Lx13B_P04",-1,4,109-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[4,-2,12,32,45]],0,[14,13,0],182],
"S01_B502S_21":["S01_B502S_21__14Lx13B_P04",-1,4,113-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[4,14,27,15,29]],0,[13,14,0],182],
"S01_B502S_41":["S01_B502S_41__14Lx13B_B01",-1,4,117-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[8,2,16,3,16]],0,[14,13,0],182],
"S01_B502S_51":["S01_B502S_51__14Lx13B_R03",-1,1,121-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],[[27,2,16,5,18]],0,[14,13,0],182],
#
"S01_B502S_00":["S01_B502S_00__14Lx13B_開始",1,1,95-44,["S01_B502S_01","S01_B502S_02","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[2,31,45,1,14]],0,[14,13,0],182],
"S01_B502S_10":["S01_B502S_10__14Lx13B_反転",4,1,109-44,["S01_B502S_11","S01_B502S_12","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[4,-2,12,32,45]],0,[14,13,0],182],
"S01_B502S_20":["S01_B502S_20__14Lx13B_正転",3,1,112-44,["S01_B502S_21","S01_B502S_22","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[4,14,27,15,29]],0,[13,14,0],182],
"S01_B502S_40":["S01_B502S_40__14Lx13B_入ブ",6,1,117-44,["S01_B502S_41","S01_B502S_42","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[8,2,16,3,16]],0,[14,13,0],182],
"S01_B502S_50":["S01_B502S_50__14Lx13B_出ブ",7,1,121-44,["S01_B502S_51","S01_B502S_52","0","0","0"],[[0,-1],[0,-1],[0,0],[0,0],[0,0]],[[27,2,16,5,18]],0,[14,13,0],182],
"S01_B502S_99":["S01_B502S_99__14Lx13B_搭載",0,1,122-44,["0","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,0],
#
"S01_B502S_02":["S01_B502S_02__14Lx13B_取付",10,0,0,["S01_B502S_03","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38*3],
"S01_B502S_03":["S01_B502S_03__14Lx13B_溶接",11,0,0,["S01_B502S_04","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,64*3],
"S01_B502S_04":["S01_B502S_04__14Lx13B_取付",12,0,0,["S01_B502S_05","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38*2],
"S01_B502S_05":["S01_B502S_05__14Lx13B_溶接",13,0,0,["S01_B502S_10","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,38],
"S01_B502S_12":["S01_B502S_12__14Lx13B_溶接",11,0,0,["S01_B502S_13","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,64*3],
"S01_B502S_13":["S01_B502S_13__14Lx13B_検査",14,1,0,["S01_B502S_20","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,0],
"S01_B502S_22":["S01_B502S_22__14Lx13B_溶接",11,0,0,["S01_B502S_23","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38],
"S01_B502S_23":["S01_B502S_23__14Lx13B_取付",10,0,0,["S01_B502S_24","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,29],
"S01_B502S_24":["S01_B502S_24__14Lx13B_溶接",11,0,0,["S01_B502S_25","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,38*2],
"S01_B502S_25":["S01_B502S_25__14Lx13B_検査",14,1,0,["S01_B502S_26","S01_B502S_27","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,0,0],
"S01_B502S_26":["S01_B502S_26__14Lx13B_甲配",16,0,0,["S01_B502S_40","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,10],
"S01_B502S_27":["S01_B502S_27__14Lx13B_鉄艤",15,0,0,["S01_B502S_40","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,16],
"S01_B502S_42":["S01_B502S_42__14Lx13B_塗装",18,0,0,["S01_B502S_50","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,90],
"S01_B502S_52":["S01_B502S_52__14Lx13B_鉄艤",15,0,0,["S01_B502S_99","0","0","0","0"],[[0,0],[0,0],[0,0],[0,0],[0,0]],0,0,1,5],
}
|