応用例…Homework
[1] ある航空機の線形状態方程式として、次を考えます。
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} \dot{x}(t)=Ax(t)+Bu(t)\\ x(t)= \left[\begin{array}{ll} \theta & pitch\ angle\\ q & pitch\ rate\\ \alpha & angle\ of\ atack\\ \eta & elevator\ deflection\\ \delta & flap\ deflection \end{array}\right],\quad u(t)= \left[\begin{array}{ll} \eta_c & elevator\ command\\ \delta_c& flap\ comannd \end{array}\right]\\ A=\left[\begin{array}{rrrrr} 0 & 1 & 0 & 0 & 0\\ 0 &-1.99 & -13.41 & -18.95 & -3.60\\ 0 & 1 & -1.74 & -0.08 & -0.59\\ 0 & 0 & 0 & -20 & 0\\ 0 & 0 & 0 & 0 & -20 \end{array}\right],\quad B=\left[\begin{array}{rr} 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 20 & 0\\ 0 & 20 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e8e30c3e5083c206da3951e3e40e9cfb_l3.png)
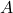 行列の固有値は次のように求められます。
行列の固有値は次のように求められます。

状態変数として、pitch angle 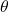 の代わりに、fligt path angle
の代わりに、fligt path angle 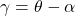 を用いると、次式となります。
を用いると、次式となります。
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \begin{array}{l} \dot{x}(t)=Ax(t)+Bu(t)\\ x(t)= \left[\begin{array}{ll} \gamma=\theta-\alpha & fligt\ path\ angle\\ q & pitch\ rate\\ \alpha & angle\ of\ atack\\ \eta & elevator\ deflection\\ \delta & flap\ deflection \end{array}\right],\quad u(t)= \left[\begin{array}{ll} \eta_c & elevator\ command\\ \delta_c& flap\ comannd \end{array}\right]\\ A=\left[\begin{array}{rrrrr} 0 & 0 & 1.74 & 0.08 & 0.59\\ 0 &-1.99 & -13.41 & -18.95 & -3.60\\ 0 & 1 & -1.74 & -0.08 & -0.59\\ 0 & 0 & 0 & -20 & 0\\ 0 & 0 & 0 & 0 & -20 \end{array}\right],\quad B=\left[\begin{array}{rr} 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 20 & 0\\ 0 & 20 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b3ae110ebe0cc483c67a6db0b309e181_l3.png)
また、評価変数として、pitch angle 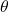 とfligt path angle
とfligt path angle 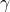 をとると、その出力方程式は次式のように与えられます。
をとると、その出力方程式は次式のように与えられます。
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} y(t)=Hx(t)\\ H= \left[\begin{array}{ccccc} 1 & 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c44cf07d269341a588b528f5aca4caf9_l3.png)
制御目的は、次図のように、pitch angle 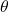 とfligt path angle
とfligt path angle 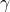 の間の非干渉化を達成し、独立して設定値に合せることです。
の間の非干渉化を達成し、独立して設定値に合せることです。
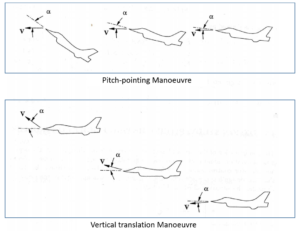
図1 航空機の操縦法
[2] モデル規範による追従制御
この場合の制御則は次のように構成されます。

●追従すべき規範モデルは
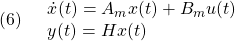
ただし
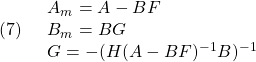
いまこの規範モデルにもたせるべき望ましい固有値を
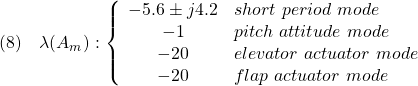
とし、また望ましいモード分布を次により指定します。
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad {\tt specpos}= \left[\begin{array}{ccc|cc} 1 & 1 & 1 & 0 & 0\\ 1 & 0 & 1 & 0 & 0\\ 0 & 1 & 1 & 0 & 0\\\hline 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\\ \end{array}\right],\quad {\tt specent}= \left[\begin{array}{rrr|rr} 0 & 0 & 1 & -1 & -1\\ 1 & -1 & 0 & -1 & -1\\ -1 & 1 & 0 & -1 & -1\\\hline -1 & -1 & -1 & 1 & -1\\ -1 & -1 & -1 & -1 & 1\\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9351aa1713d68cc420ab75e44c211a51_l3.png)
ここで、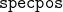 は望ましい固有ベクトルの要素を指定する場合1、指定しない場合0で表した行列、
は望ましい固有ベクトルの要素を指定する場合1、指定しない場合0で表した行列、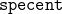 は望ましい固有ベクトルの要素が非零指定の場合1、零の場合0、非零任意の場合-1で表した行列です。
は望ましい固有ベクトルの要素が非零指定の場合1、零の場合0、非零任意の場合-1で表した行列です。
このとき以下に示すプログラムを使って、次が得られます。
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{l} F=WV^{-1} =\left[\begin{array}{rrrrr} -1.9338 & -0.5744 & -2.1188 & 0.4750 & 0.1066\\ 1.9571 & 0.2253 & 3.1273 & -0.0694 & -0.0515 \end{array}\right]\\ W=\left[\begin{array}{rrrrr} 0.8445 & 1.9935 & -0.2742 & 0 & 0\\ -2.7055 & 1.2780 & 0.1767 & 0 & 0 \end{array}\right]\\ V=\left[\begin{array}{rrrrr} 0 & -0.0000 & 0.6667 & 0.0030 & -0.0313\\ 1.0000 & -9.5000 & -0.3333 & 0.9964 & 0.1493\\ -0.9286 & 1.0000 & -0.3333 & -0.0528 & 0.0238\\ -1.8252 & -2.2364 & 0.2886 & 1.0000 & -0.0649\\ 2.9860 & -2.6459 & -0.1860 & -0.0825 & 1.0000 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b86eb8a3dc0f557c2de880c6fc23d3ee_l3.png)
●ここでは、スイッチング関数
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad s(t)= \underbrace{ \left[\begin{array}{cc} M & I \end{array}\right] }_{S} x(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-56614033be22d4d00a72ea0df7a59756_l3.png)
を構成するために
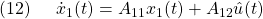
を2次形式評価関数
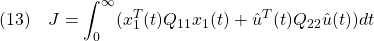
を最小にする
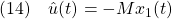
を求めます。
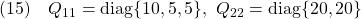
と選ぶとき、スイッチング関数を決める行列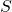 が、次のように得られます。
が、次のように得られます。
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad S=\left[\begin{array}{rrr|rr} 0.7025 & 0.4209 & 0.1894 & -1 & 0\\ -0.0810 & 0.0635 & 0.0267 & 0 & -1\\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1a54c401f08a53756e3cdbf9bd5fb79c_l3.png)
●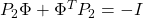 を満たす
を満たす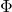 と
と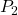 は、たとえば次のように定めます。
は、たとえば次のように定めます。
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad \underbrace{ \left[\begin{array}{rr} 0.025 & 0\\ 0 & 0.025 \end{array}\right] }_{P_2} \underbrace{ \left[\begin{array}{rr} 20 & 0\\ 0 & 20 \end{array}\right] }_{\Phi} +(*)^T=-I }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dc78c4ca1633a74198c3d266be410408_l3.png)
このときSMC則における行列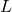 は次のように計算されます。
は次のように計算されます。
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad L=\left[\begin{array}{rrrrr} -1.2285 & -0.1858 & -2.1624 & 0.0782 & 0.0460\\ 1.8631 & 0.2827 & 3.0804 & -0.1299 & -0.0060 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fdc8370cdd16784063df9e022afba091_l3.png)
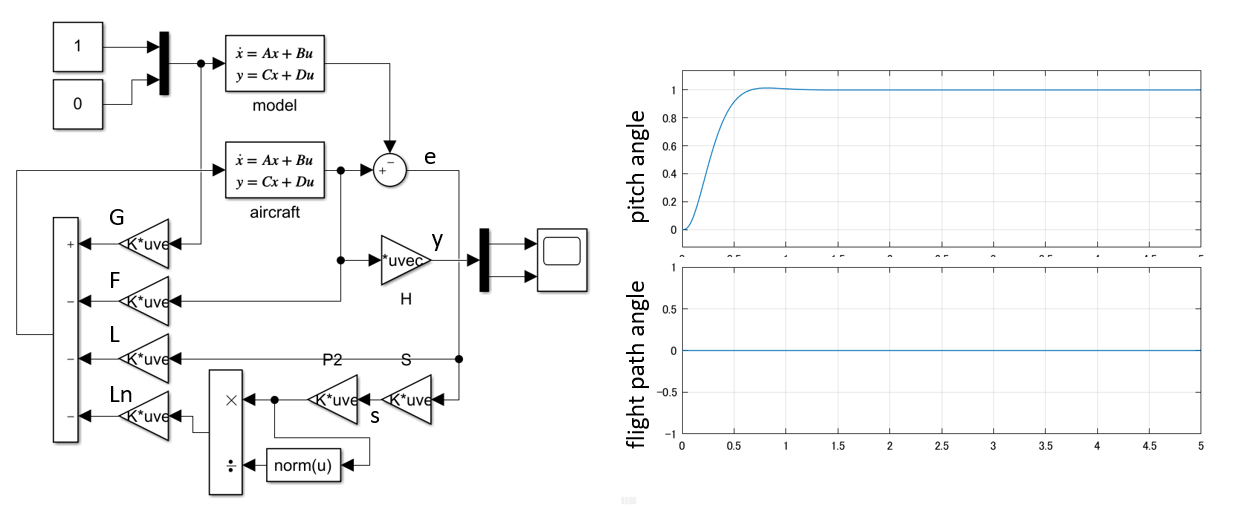 図2 モデル規範法によるSMC制御系応答
図2 モデル規範法によるSMC制御系応答

| MATLAB |
%cAIRCRAFT_smcm.m
%-----
clear all, close all
A= [0 0 1.74 0.08 0.59;
0 -1.99 -13.41 -18.95 -3.6;
0 1 -1.74 -0.08 -0.59;
0 0 0 -20 0;
0 0 0 0 -20];
B=[0 0;0 0;0 0;20 0;0 20];
%-----
lambda=[-5.6 4.2 -1 -20 -20];
nocomp=1;
%固有ベクトルの非零要素の位置 (1:指定、0:指定せず)
specpos=[ 1 1 1 0 0;
1 0 1 0 0;
0 1 1 0 0;
0 0 0 1 0;
0 0 0 0 1]
%固有ベクトルの要素の値 (0:零、1:非零指定、-1:非零任意)
specent=[ 0 0 1 -1 -1;
1 -1 0 -1 -1;
-1 1 0 -1 -1;
-1 -1 -1 1 -1;
-1 -1 -1 -1 1]
F=vplace2(A,B,lambda,nocomp,specpos,specent)
pl=eig(A-B*F)
%-----
H=[1 0 1 0 0;1 0 0 0 0];
Am=A-B*F;
G=-inv(H*(Am\B));
Bm=B*G;
%-----
Q=diag([10,5,5,20,20]);
S=swflqr(A,B,Q)
%-----
P2=diag([0.025,0.025]);
Phi=-20/0.025*P2;
Check=P2*Phi+Phi*P2
L=inv(S*B)*(S*Am-Phi*S)
Ln=inv(S*B)
%-----
sim('AIRCRAFT_smcm_2015a.mdl')
%-----
%eof
|
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} \dot{x}(t)=Ax(t)+Bu(t)\\ x(t)= \left[\begin{array}{ll} \theta & pitch\ angle\\ q & pitch\ rate\\ \alpha & angle\ of\ atack\\ \eta & elevator\ deflection\\ \delta & flap\ deflection \end{array}\right],\quad u(t)= \left[\begin{array}{ll} \eta_c & elevator\ command\\ \delta_c& flap\ comannd \end{array}\right]\\ A=\left[\begin{array}{rrrrr} 0 & 1 & 0 & 0 & 0\\ 0 &-1.99 & -13.41 & -18.95 & -3.60\\ 0 & 1 & -1.74 & -0.08 & -0.59\\ 0 & 0 & 0 & -20 & 0\\ 0 & 0 & 0 & 0 & -20 \end{array}\right],\quad B=\left[\begin{array}{rr} 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 20 & 0\\ 0 & 20 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e8e30c3e5083c206da3951e3e40e9cfb_l3.png)
![]() 行列の固有値は次のように求められます。
行列の固有値は次のように求められます。
![]() の代わりに、fligt path angle
の代わりに、fligt path angle ![]() を用いると、次式となります。
を用いると、次式となります。![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \begin{array}{l} \dot{x}(t)=Ax(t)+Bu(t)\\ x(t)= \left[\begin{array}{ll} \gamma=\theta-\alpha & fligt\ path\ angle\\ q & pitch\ rate\\ \alpha & angle\ of\ atack\\ \eta & elevator\ deflection\\ \delta & flap\ deflection \end{array}\right],\quad u(t)= \left[\begin{array}{ll} \eta_c & elevator\ command\\ \delta_c& flap\ comannd \end{array}\right]\\ A=\left[\begin{array}{rrrrr} 0 & 0 & 1.74 & 0.08 & 0.59\\ 0 &-1.99 & -13.41 & -18.95 & -3.60\\ 0 & 1 & -1.74 & -0.08 & -0.59\\ 0 & 0 & 0 & -20 & 0\\ 0 & 0 & 0 & 0 & -20 \end{array}\right],\quad B=\left[\begin{array}{rr} 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 20 & 0\\ 0 & 20 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b3ae110ebe0cc483c67a6db0b309e181_l3.png)
![]() とfligt path angle
とfligt path angle ![]() をとると、その出力方程式は次式のように与えられます。
をとると、その出力方程式は次式のように与えられます。![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} y(t)=Hx(t)\\ H= \left[\begin{array}{ccccc} 1 & 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c44cf07d269341a588b528f5aca4caf9_l3.png)
![]() とfligt path angle
とfligt path angle ![]() の間の非干渉化を達成し、独立して設定値に合せることです。
の間の非干渉化を達成し、独立して設定値に合せることです。

![]()
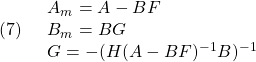
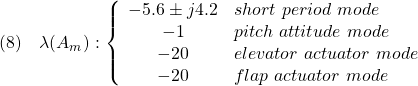
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad {\tt specpos}= \left[\begin{array}{ccc|cc} 1 & 1 & 1 & 0 & 0\\ 1 & 0 & 1 & 0 & 0\\ 0 & 1 & 1 & 0 & 0\\\hline 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\\ \end{array}\right],\quad {\tt specent}= \left[\begin{array}{rrr|rr} 0 & 0 & 1 & -1 & -1\\ 1 & -1 & 0 & -1 & -1\\ -1 & 1 & 0 & -1 & -1\\\hline -1 & -1 & -1 & 1 & -1\\ -1 & -1 & -1 & -1 & 1\\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9351aa1713d68cc420ab75e44c211a51_l3.png)
![]() は望ましい固有ベクトルの要素を指定する場合1、指定しない場合0で表した行列、
は望ましい固有ベクトルの要素を指定する場合1、指定しない場合0で表した行列、![]() は望ましい固有ベクトルの要素が非零指定の場合1、零の場合0、非零任意の場合-1で表した行列です。
は望ましい固有ベクトルの要素が非零指定の場合1、零の場合0、非零任意の場合-1で表した行列です。![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{l} F=WV^{-1} =\left[\begin{array}{rrrrr} -1.9338 & -0.5744 & -2.1188 & 0.4750 & 0.1066\\ 1.9571 & 0.2253 & 3.1273 & -0.0694 & -0.0515 \end{array}\right]\\ W=\left[\begin{array}{rrrrr} 0.8445 & 1.9935 & -0.2742 & 0 & 0\\ -2.7055 & 1.2780 & 0.1767 & 0 & 0 \end{array}\right]\\ V=\left[\begin{array}{rrrrr} 0 & -0.0000 & 0.6667 & 0.0030 & -0.0313\\ 1.0000 & -9.5000 & -0.3333 & 0.9964 & 0.1493\\ -0.9286 & 1.0000 & -0.3333 & -0.0528 & 0.0238\\ -1.8252 & -2.2364 & 0.2886 & 1.0000 & -0.0649\\ 2.9860 & -2.6459 & -0.1860 & -0.0825 & 1.0000 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b86eb8a3dc0f557c2de880c6fc23d3ee_l3.png)
![]()
![]()
![]()
![]()
![]()
![]() が、次のように得られます。
が、次のように得られます。![]()
![]() を満たす
を満たす![]() と
と![]() は、たとえば次のように定めます。
は、たとえば次のように定めます。![Rendered by QuickLaTeX.com \displaystyle{(17)\quad \underbrace{ \left[\begin{array}{rr} 0.025 & 0\\ 0 & 0.025 \end{array}\right] }_{P_2} \underbrace{ \left[\begin{array}{rr} 20 & 0\\ 0 & 20 \end{array}\right] }_{\Phi} +(*)^T=-I }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dc78c4ca1633a74198c3d266be410408_l3.png)
![]() は次のように計算されます。
は次のように計算されます。![]()
 図2 モデル規範法によるSMC制御系応答
図2 モデル規範法によるSMC制御系応答