スイッチング関数(2)
[1] 状態方程式とスイッチング関数は次の標準形をとるように座標変換されていると仮定します。
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot x(t)} = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a4c8217b8c641b28c9d2c724fc2462cb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} \ (M=S_2^{-1}S_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0639c7053096db5f35e066d8fec1086a_l3.png)
このとき、等価制御
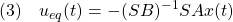
による閉ループ系は次式で表されました。
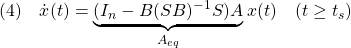
ここで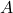 、
、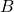 、
、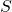 は、(1)と(2)で与えられるとすると
は、(1)と(2)で与えられるとすると
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} A_{eq}= \underbrace{ \left[\begin{array}{cc} I & 0 \\ -M & 0 \\ \end{array}\right] }_{I_n-B(SB)^{-1}S} \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right]= \left[\begin{array}{cc} A_{11} & A_{12} \\ -MA_{11} & -MA_{12} \\ \end{array}\right]\\ = \left[\begin{array}{cc} I & 0 \\ -M & I \\ \end{array}\right] \left[\begin{array}{cc} \bar{A}_{11} & A_{12} \\ 0 & 0 \\ \end{array}\right] \left[\begin{array}{cc} I & 0 \\ -M & I \\ \end{array}\right]^{-1} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e3ecd7fa57b5a4b72c9f1811a79dd648_l3.png)
となって、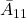 が安定行列なので、
が安定行列なので、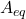 は
は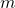 個の零固有値を持ちます。一方、
個の零固有値を持ちます。一方、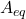 の非零固有値
の非零固有値 に対応する固有ベクトルを
に対応する固有ベクトルを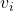 とすると、
とすると、
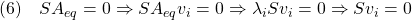
すなわち
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad { \boxed{S[v_1\cdots v_{n-m}]=0 % \Rightarrow [v_1\cdots v_{n-m}]^TS^T=0}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2f0ecfa9ddb2fff39d1fc2e0a565febb_l3.png)
が成り立ちます。したがって、まず等価制御による閉ループ系の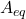 が望ましい固有値・固有ベクトルをもつように設計して、(7)から
が望ましい固有値・固有ベクトルをもつように設計して、(7)から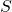 を決定することが考えられます。
を決定することが考えられます。
● 1入力系の場合は固有ベクトル設定の自由度はありませんが、多入力系の場合は固有ベクトルの向きを設定する必要があり、これは元の状態方程式(状態変数の並び)に対して与えます。そこで(7)が元の状態方程式ではどう変わるかを調べておきます。
元の状態方程式
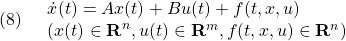
に対する標準形(1)は、適当な直交行列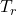 座標による座標変換
座標による座標変換
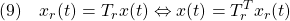
を行って(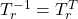 に注意)
に注意)
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{x}_{r1}(t)\\ \dot{x}_{r2}(t) \end{array}\right] }_{\dot{x}_r(t)} = \underbrace{ \left[\begin{array}{cc} A_{r11} & A_{r12} \\ A_{r21} & A_{r22} \\ \end{array}\right] }_{A_r=T_rAT_r^T} \underbrace{ \left[\begin{array}{c} x_{r1}(t)\\ x_{r2}(t) \end{array}\right] }_{x_r(t)} + \underbrace{ \left[\begin{array}{c} 0\\ \Sigma_1V^T \end{array}\right] }_{B_r=T_rB} u(t)\\ + \underbrace{ \left[\begin{array}{l} f_{ru}(t,x)\\ f_{rm}(t,x,u) \end{array}\right] }_{f_r(t,x,u)=T_rf(t,x,u)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ffa705d6b2bd55a3734da676f36934df_l3.png)
のように得られたものでした。また(2)は次式に
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_{r1} & S_{r2} \\ \end{array}\right] }_{S_r=ST_r^T} \underbrace{ \left[\begin{array}{c} x_{r1}(t)\\ x_{r2}(t) \end{array}\right] }_{x_r(t)=T_rx(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5f1e30d6fccc2ee648cf30ffd07ad4c3_l3.png)
に、(7)は次式に相当します。
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad S_r[v_{r1}\cdots v_{r,n-m}]=0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-00ced896c207abf2504b2aad521de145_l3.png)
いま、元の状態空間での固有ベクトル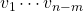 は、座標変換後には
は、座標変換後には
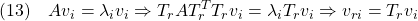
に変わることに注意します。(12)から
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad S_rT_rT_r^T[v_{r1}\cdots v_{r,n-m}]=S[v_1\cdots v_{n-m}]=0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2d7528d17c173cabfc7fabb1a6a954ea_l3.png)
を得ます。これから元の状態方程式に対するスイッチング関数と固有ベクトルについても、(12)と同様の関係が成り立つと言えます。すなわち固有ベクトル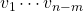 は元の状態空間で与えておいて、(14)から
は元の状態空間で与えておいて、(14)から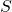 を決定してよいことがわかります。
を決定してよいことがわかります。
演習C41…Flipped Classroom
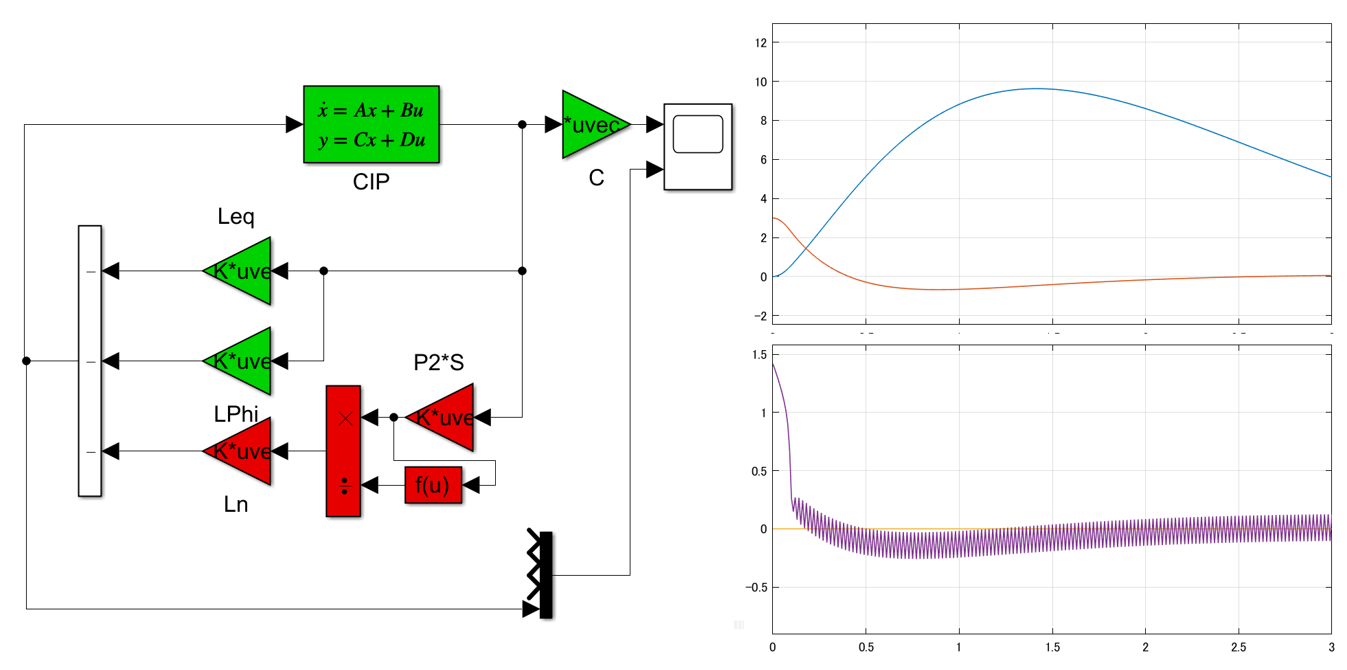
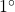 スイッチング関数決定プログラムswfvplを用いて、図1の台車駆動型倒立振子を安定化する次のSMC則を求めよ。
スイッチング関数決定プログラムswfvplを用いて、図1の台車駆動型倒立振子を安定化する次のSMC則を求めよ。
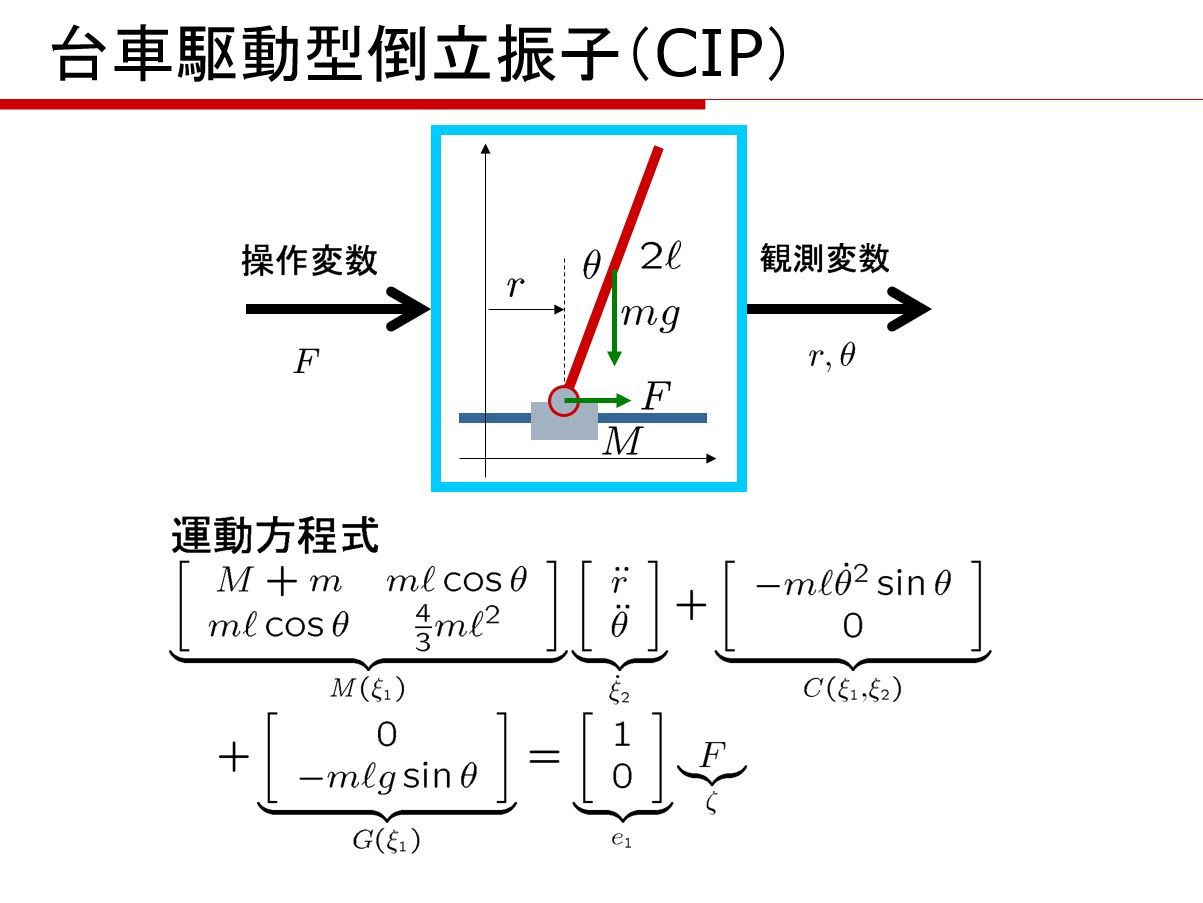 図1 台車駆動型倒立振子
図1 台車駆動型倒立振子
| MATLAB |
%cCIP_smc2.m
%-----
clear all, close all
global mc m ell g th0
mc=1; m=0.1; ell=0.2; g=9.8;
ths=0; %input('ths = <0,180> ')/180*pi;
th0=3/180*pi; %input('th(0) = <0,180> ')/180*pi;
%-----
A=[zeros(2,2) eye(2);zeros(2,4)];
A(3,1)=0;
A(3,2)=-3*m*g/(m+4*mc);
A(4,1)=0;
A(4,2)=3*(m+mc)*g/((m+4*mc)*ell);
B=zeros(4,1);
B(3)=4/(m+4*mc);
B(4)=-3/((m+4*mc)*ell);
C=diag([100 180/pi])*eye(2,4);
%-----
lambda=[-0.8 0.5 -3];
nocomp=1;
specpos=rand(4,3)
specent=rand(4,3)
S=swfvpl(A,B,lambda,nocomp,specpos,specent)
%-----
Phi=-0.1;
P2=0.5*inv(-Phi);
Check=P2*Phi+Phi*P2
P2S=P2*S;
Leq=inv(S*B)*S*A;
LPhi=-inv(S*B)*Phi*S;
L=Leq+LPhi;
rho=0.6;
Ln=inv(S*B)*rho;
%-----
x0=[0;th0;0;0];
sim('CIP_smc_2015a.mdl')
%-----
%eof
|
Note C41 スイッチング関数決定プログラム2
Edwards and Spurgeon によって、(26)から、スイッチング関数の行列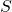 を求めるプログラムswfvplが開発されています。
を求めるプログラムswfvplが開発されています。
| MATLAB |
%test_swfvpl.m
%-----
clear all, close all
A=[0 1 0;
0 0 1;
0 0 0];
B=[0;
0;
1];
%-----
lambda=[-2 -3];
nocomp=0;
%固有ベクトルの要素の指定の有無 (1:指定、0:任意)
specpos=rand(3,3)
%固有ベクトルの要素の値 (0:零指定、1:非零指定、-1:非零任意)
specent=rand(3,3)
S=swfvpl(A,B,lambda,nocomp,specpos,specent)
Leq=inv(S*B)*S*A;
[V,pl]=eig(A-B*Leq)
%-----
lambda=[-1 1];
nocomp=1;
%固有ベクトルの要素の指定の有無 (1:指定、0:任意)
specpos=rand(3,3)
%固有ベクトルの要素の値 (0:零指定、1:非零指定、-1:非零任意)
specent=rand(3,3)
S=swfvpl(A,B,lambda,nocomp,specpos,specent)
Leq=inv(S*B)*S*A;
[V,pl]=eig(A-B*Leq)
%-----
%eof
|
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot x(t)} = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a4c8217b8c641b28c9d2c724fc2462cb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} \ (M=S_2^{-1}S_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0639c7053096db5f35e066d8fec1086a_l3.png)
![]()
![]()
![]() 、
、![]() 、
、![]() は、(1)と(2)で与えられるとすると
は、(1)と(2)で与えられるとすると![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} A_{eq}= \underbrace{ \left[\begin{array}{cc} I & 0 \\ -M & 0 \\ \end{array}\right] }_{I_n-B(SB)^{-1}S} \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right]= \left[\begin{array}{cc} A_{11} & A_{12} \\ -MA_{11} & -MA_{12} \\ \end{array}\right]\\ = \left[\begin{array}{cc} I & 0 \\ -M & I \\ \end{array}\right] \left[\begin{array}{cc} \bar{A}_{11} & A_{12} \\ 0 & 0 \\ \end{array}\right] \left[\begin{array}{cc} I & 0 \\ -M & I \\ \end{array}\right]^{-1} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e3ecd7fa57b5a4b72c9f1811a79dd648_l3.png)
![]() が安定行列なので、
が安定行列なので、![]() は
は![]() 個の零固有値を持ちます。一方、
個の零固有値を持ちます。一方、![]() の非零固有値
の非零固有値![]() に対応する固有ベクトルを
に対応する固有ベクトルを![]() とすると、
とすると、![]()
![]()
![]() が望ましい固有値・固有ベクトルをもつように設計して、(7)から
が望ましい固有値・固有ベクトルをもつように設計して、(7)から![]() を決定することが考えられます。
を決定することが考えられます。![]()
![]() 座標による座標変換
座標による座標変換![]()
![]() に注意)
に注意)![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{x}_{r1}(t)\\ \dot{x}_{r2}(t) \end{array}\right] }_{\dot{x}_r(t)} = \underbrace{ \left[\begin{array}{cc} A_{r11} & A_{r12} \\ A_{r21} & A_{r22} \\ \end{array}\right] }_{A_r=T_rAT_r^T} \underbrace{ \left[\begin{array}{c} x_{r1}(t)\\ x_{r2}(t) \end{array}\right] }_{x_r(t)} + \underbrace{ \left[\begin{array}{c} 0\\ \Sigma_1V^T \end{array}\right] }_{B_r=T_rB} u(t)\\ + \underbrace{ \left[\begin{array}{l} f_{ru}(t,x)\\ f_{rm}(t,x,u) \end{array}\right] }_{f_r(t,x,u)=T_rf(t,x,u)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ffa705d6b2bd55a3734da676f36934df_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_{r1} & S_{r2} \\ \end{array}\right] }_{S_r=ST_r^T} \underbrace{ \left[\begin{array}{c} x_{r1}(t)\\ x_{r2}(t) \end{array}\right] }_{x_r(t)=T_rx(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5f1e30d6fccc2ee648cf30ffd07ad4c3_l3.png)
![]()
![]() は、座標変換後には
は、座標変換後には![]()
![]()
![]() は元の状態空間で与えておいて、(14)から
は元の状態空間で与えておいて、(14)から![]() を決定してよいことがわかります。
を決定してよいことがわかります。![]() スイッチング関数決定プログラムswfvplを用いて、図1の台車駆動型倒立振子を安定化する次のSMC則を求めよ。
スイッチング関数決定プログラムswfvplを用いて、図1の台車駆動型倒立振子を安定化する次のSMC則を求めよ。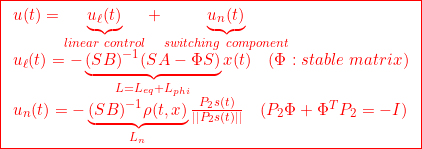
 図1 台車駆動型倒立振子
図1 台車駆動型倒立振子
![]() を求めるプログラムswfvplが開発されています。
を求めるプログラムswfvplが開発されています。