補償器によるSM制御…Homework
[1] 制御対象
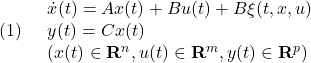
に対するSM制御則の線形制御部を、補償器
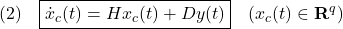
を用いて実現することを考えます。このときのスイッチング関数を
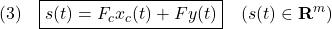
とします。
●出力FB型SM制御(p>m)の議論により、次のSM標準形を得ているものとします。
![Rendered by QuickLaTeX.com \displaystyle{(18.1^*)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x'''_1(t)\\ \dot x'''_2(t) \end{array}\right] }_{\dot{x}'''(t)} = \underbrace{ \left[\begin{array}{ccc|c} A_{11}^o & A_{12}^o & A_{121}^m & A_{121}\\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m & A_{1221}\\ 0_{p-m\times r} & A_{21}^o & A_{22}^m & A_{1222}\\\hline A_{2120} & A_{2121} & A_{2122} & A_{22} \end{array}\right] }_{(T_aT_bT_c)A(T_aT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] }_{x'''(t)}\\ + \underbrace{ \left[\begin{array}{c} 0_{r\times m} \\ 0_{n-p-r\times m} \\ 0_{p-m\times m} \\\hline B_2 \end{array}\right] }_ {(T_aT_bT_c)B} \underbrace{(u(t)+\xi(t,x,u))}_{u'(t)}\\ (A_{11}^o\in{\rm\bf R}^{r\times r},A_{22}^o\in{\rm\bf R}^{n-p-r\times n-p-r},A_{22}^m\in{\rm\bf R}^{p-m\times p-m},A_{22}\in{\rm\bf R}^{m\times m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-712c9ee206bbfdfc0320ee7fb2c01281_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(18.2^*)\quad \begin{array}{l} y(t) = \underbrace{ \left[\begin{array}{cc} 0_{p\times n-p} & T \\ \end{array}\right] }_{C(T_aT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] }_{x'''(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c2d502c3e8c7b30de092731cc5418e3d_l3.png)
このとき、![Rendered by QuickLaTeX.com C_1=\left[\begin{array}{cc} 0_{p-m\times n-p} & I_{p-m} \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4494ac3aaaaae00e15a3621e40125c51_l3.png) とおくと
とおくと
![Rendered by QuickLaTeX.com \displaystyle{(2')\quad \begin{array}{l} \dot{x}_c(t)=Hx_c(t)+Dy(t)\\ =Hx_c(t)+ \left[\begin{array}{cc} 0_{p\times n-p} & DT \\ \end{array}\right] %\underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] %}_{x'''(t)} \\ =Hx_c(t)+ \left[\begin{array}{cc} D_1C_1 & D_2 \\ \end{array}\right] %\underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] %}_{x'''(t)} \\ =Hx_c(t)+D_1C_1x'''_1(t)+D_2x'''_2(t)\\ (DT=\left[\begin{array}{cc} D_1 & D_2 \end{array}\right], D_1\in{\rm\bf R}^{m\times p-m}, D_2\in{\rm\bf R}^{m\times m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9c519f23b2642a1398b44d297648888d_l3.png)
および
![Rendered by QuickLaTeX.com \displaystyle{(3')\quad \begin{array}{l} s(t)=F_cx_c(t)+Fy(t)\\ =Hx_c(t)+ \left[\begin{array}{cc} 0_{p\times n-p} & FT \\ \end{array}\right] %\underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] %}_{x'''(t)} \\ =Hx_c(t)+ \left[\begin{array}{cc} F_1C_1 & F_2 \\ \end{array}\right] %\underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] %}_{x'''(t)} \\ =Hx_c(t)+F_1C_1x'''_1(t)+F_2x'''_2(t)\\ (FT=\left[\begin{array}{cc} F_1 & F_2 \end{array}\right], F_1\in{\rm\bf R}^{m\times p-m}, F_2\in{\rm\bf R}^{m\times m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c3a63f48d662d8ce45ee20bfb786b893_l3.png)
●(18.1 )と(2′)を結合し、
)と(2′)を結合し、![Rendered by QuickLaTeX.com \tilde{C}_1=\left[\begin{array}{cc} 0_{p-m\times n-p-r} & I_{p-m} \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4883704e3b2d46fc1e351ef0e4b239ce_l3.png) を用いて、次式を得ます。
を用いて、次式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x'''_1(t)\\\hline \dot x'''_2(t)\\\hline\hline \dot x_c(t) \end{array}\right] }_{\dot{x}'''(t)} = \left[\begin{array}{c|c||c} \left.\begin{array}{ccc} A_{11}^o & A_{12}^o & A_{121}^m \\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m \\ 0_{p-m\times r} & A_{21}^o & A_{22}^m \\ \end{array}\right.& \left.\begin{array}{cc} A_{121}\\ A_{1221}\\ A_{1222} \end{array}\right.& \left.\begin{array}{cc} 0_{r\times q} \\ 0_{n-p-r\times q} \\ 0_{p-m\times q} \end{array}\right. \\\hline \left.\begin{array}{ccc} A_{211} & A_{2121} &A_{2122} \end{array}\right.& \left.\begin{array}{cc} A_{22} \end{array}\right.& 0_{m\times q} \\\hline\hline %D_1C_1 \left.\begin{array}{cc} 0_{q\times r} & D_1\tilde{C}_1 \end{array}\right. & D_2 & H \end{array}\right]\\ \times \underbrace{ \left[\begin{array}{c} x'''_1(t)\\\hline x'''_2(t)\\\hline\hline x_c(t) \end{array}\right] }_{x'''(t)} + \left[\begin{array}{c} 0_{r\times m} \\ 0_{n-p-r\times m} \\ 0_{p-m\times m} \\\hline B_2\\\hline\hline 0_{q\times m} \end{array}\right] u'(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1968121e3a5d1a000f172ea9ce55a016_l3.png)
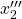 と
と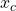 を入れ替えて
を入れ替えて
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x'''_1(t)\\\hline \dot x_c(t)\\\hline\hline \dot x'''_2(t) \end{array}\right] }_{\dot{x}'''(t)} = \left[\begin{array}{c|c||c} \left.\begin{array}{ccc} A_{11}^o & A_{12}^o & A_{121}^m \\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m \\ 0_{p-m\times r} & A_{21}^o & A_{22}^m \\ \end{array}\right.& \left.\begin{array}{cc} 0_{r\times q} \\ 0_{n-p-r\times q} \\ 0_{p-m\times q} \end{array}\right. & \left.\begin{array}{cc} A_{121}\\ A_{1221}\\ A_{1222} \end{array}\right. \\\hline %D_1C_1 \left.\begin{array}{ccc} 0_{q\times r} & D_1\tilde{C}_1 \end{array}\right. & \left.\begin{array}{cc} H \end{array}\right. & D_2 \\\hline\hline \left.\begin{array}{ccc} A_{211} & A_{2121} &A_{2122} \end{array}\right. & 0_{m\times q} & A_{22} \end{array}\right]\\ \times \underbrace{ \left[\begin{array}{c} x'''_1(t)\\\hline x_c(t)\\\hline\hline x'''_2(t) \end{array}\right] }_{x'''(t)} + \left[\begin{array}{c} 0_{r\times m} \\ 0_{n-p-r\times m} \\ 0_{p-m\times m} \\\hline 0_{q\times m}\\\hline\hline B_2\\ \end{array}\right] u'(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-954b2e74e37e5828afcfbe39a920d5cb_l3.png)
ここで、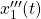 を
を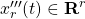 、
、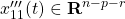 、
、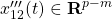 に分割し、座標変換
に分割し、座標変換
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} x'''_r(t)\\ x'''_{11}(t)\\ x'''_{12}(t)\\\hline x_c(t)\\\hline\hline x''''_2(t)\\ \end{array}\right] }_{x''''(t)} = \underbrace{ \left[\begin{array}{ccc|c||c} I_{r} & 0 & 0 & 0& 0 \\ 0 & I_{n-p-r} & 0 & 0& 0 \\ 0 & 0 & I_{p-m} & 0 & 0\\\hline 0 & 0 & 0 & I_q &0 \\\hline\hline 0 & 0 & K & K_c & I_m \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x'''_r(t)\\ x'''_{11}(t)\\ x'''_{12}(t)\\\hline x_c(t)\\\hline\hline x'''_2(t)\\ \end{array}\right] }_{x'''(t)}\\ (K=F_2^{-1}F_1, K_c=F_2^{-1}F_c) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bb2718c0970f9bbdf8747a901f89c9ab_l3.png)
を行って、次式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x'''_r(t)\\ \dot x'''_{11}(t)\\ \dot x'''_{12}(t)\\\hline \dot x_c(t)\\\hline \dot x''''_2(t) \end{array}\right] }_{\dot{x}''''(t)} = \left[\begin{array}{c|c} \left[\begin{array}{c|c} \left.\begin{array}{ccc} A_{11}^o & A_{12}^o & A_{121}^m \\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m \\ 0_{p-m\times r} & A_{21}^o & A_{22}^m \\ \end{array}\right. & \left.\begin{array}{cc} 0_{r\times q} \\ 0_{n-p-r\times q} \\ 0_{p-m\times q} \end{array}\right. \\\hline %D_1C_1 \left.\begin{array}{cc} 0_{q\times r} & D_1\tilde{C}_1 \end{array}\right. & H \end{array}\right]\\ - \left[\begin{array}{cc} A_{121}\\ A_{1221}\\ A_{1222}\\\hline D_2 \end{array}\right] \left[\begin{array}{ccccc} 0_{m\times r} & K\tilde{C}_1 & K_c \end{array}\right] & \left.\begin{array}{cc} A_{121}\\ A_{1221}\\ A_{1222}\\\hline D_2 \end{array}\right. \\\hline \left.\begin{array}{ccc|c} A_{211} & A_{2121} &A_{2122} & 0_{m\times q} \end{array}\right. & A_{22} \end{array}\right]\\ \times \underbrace{ \left[\begin{array}{c} x'''_r(t)\\ x'''_{11}(t)\\ x'''_{12}(t)\\\hline x_c(t)\\\hline x''''_2(t)\\ \end{array}\right] }_{x''''(t)} + \left[\begin{array}{c} 0_{r\times m} \\ 0_{n-p-r\times m} \\ 0_{p-m\times m} \\\hline 0_{q\times m}\\\hline B_2 \end{array}\right] u'(t)\\ = \underbrace{ \left[\begin{array}{c|c} \left.\begin{array}{c|c} \left.\begin{array}{ccc} A_{11}^o & A_{12}^o & A_{121}^m-A_{121}K \\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m-A_{1221}K \\ 0_{p-m\times r} & A_{21}^o & A_{22}^m-A_{1222}K \end{array}\right. & \left.\begin{array}{cc} -A_{121}K_c\\ -A_{1221}K_c\\ -A_{1222}K_c\\ \end{array}\right. \\\hline %(D_1-D_2K)C_1 \left.\begin{array}{cc} 0_{q\times r} & D(D_1-D_2K)\tilde{C}_1 \end{array}\right. & H-D_2K_c \end{array}\right. & \left.\begin{array}{cc} A_{121}\\ A_{1221}\\ A_{1222}\\\hline D_2 \end{array}\right.\\\hline \left.\begin{array}{ccc|c} A_{211} & A_{2121} &A_{2122} & 0_{m\times q} \end{array}\right. & A_{22} \end{array}\right] }_{ \left[\begin{array}{cc} \tilde{\cal A}_{11} & \tilde{\cal A}_{12} \\ \tilde{\cal A}_{21} & \tilde{\cal A}_{22} \end{array}\right]} \\ \times \underbrace{ \left[\begin{array}{c} x'''_r(t)\\ x'''_{11}(t)\\ x'''_{12}(t)\\\hline x_c(t)\\\hline x''''_2(t)\\ \end{array}\right] }_{x''''(t)} + \left[\begin{array}{c} 0_{r\times m} \\ 0_{n-p-r\times m} \\ 0_{p-m\times m} \\\hline 0_{q\times m}\\\hline B_2 \end{array}\right] u'(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1a787fcbba242095e1c00febe98dcfe6_l3.png)
以前の議論と同様に、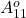 が安定行列であることを前提として、
が安定行列であることを前提として、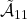 を安定行列とする
を安定行列とする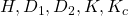 を求めます。
を求めます。
[2] 一つのアプローチとして
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \left[\begin{array}{c} \dot x'''_{11}(t)\\ \dot x'''_{12}(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} A_{22}^o & A_{122}^m \\ A_{21}^o & A_{22}^m \\ \end{array}\right] }_{\tilde{A}_{11}} \left[\begin{array}{c} x'''_{11}(t)\\ x'''_{12}(t) \end{array}\right] + \underbrace{ \left[\begin{array}{cc} A_{1221} \\ A_{1222} \\ \end{array}\right] }_{A_{122}} \underbrace{x'''_{2}(t)}_{\tilde u(t)} \\ \underbrace{x'''_{12}(t)}_{\tilde y(t)} = \underbrace{ \left[\begin{array}{cc} 0_{p-m\times n-p-r} & I_{p-m} \end{array}\right] }_{\tilde{C}_1}} \left[\begin{array}{c} x'''_{11}(t)\\ x'''_{12}(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0a20a7d2962db1ada4badc2bf0778a94_l3.png)
に対する安定化状態フィードバック則を
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \tilde u(t)= \left[\begin{array}{cc} K_1 & K_2 \end{array}\right] \left[\begin{array}{c} x'''_{11}(t)\\ x'''_{12}(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1d4056e4bd9f566bc077ce78090defe8_l3.png)
とします。ここで、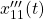 のすべての要素は観測できないので、関数オブザーバ
のすべての要素は観測できないので、関数オブザーバ
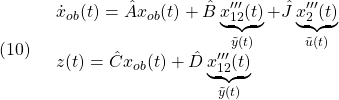
を考え、この出力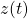 に安定化状態フィードバック則
に安定化状態フィードバック則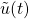 を推定させます。すなわち
を推定させます。すなわち
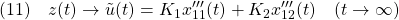
そのためには、関数オブザーバの状態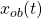 も適当な状態の線形関数を推定する必要があり、これを次のように表します。
も適当な状態の線形関数を推定する必要があり、これを次のように表します。
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad x_{ob}(t)\rightarrow \underbrace{ \left[\begin{array}{cc} I_{n-p-r} & -L^o \end{array}\right] }_{U} \left[\begin{array}{c} x'''_{11}(t)\\ x'''_{12}(t) \end{array}\right]= x'''_{11}(t)-L^ox'''_{12}(t) \quad(t\rightarrow\infty) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7c76952731eb4799d0b3b24379431e11_l3.png)
いま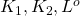 を適当に与えたとき、関数オブザーバのパラメータは
を適当に与えたとき、関数オブザーバのパラメータは
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \left[\begin{array}{c} U\tilde{A}_{11}\\ \left[\begin{array}{cc} {K}_1 & {K}_2 \end{array}\right] \end{array}\right] = \left[\begin{array}{cc} \hat{A} & \hat{B}\\ \hat{C} & \hat{D} \end{array}\right] \left[\begin{array}{c} U\\ \tilde{C}_1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6b6bde88116790420c82bd8842dae055_l3.png)
を解いて
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \begin{array}{l} \left[\begin{array}{cc} \hat{A} & \hat{B}\\ \hat{C} & \hat{D} \end{array}\right] = \left[\begin{array}{c} U\tilde{A}_{11}\\ \left[\begin{array}{cc} {K}_1 & {K}_2 \end{array}\right] \end{array}\right] \left[\begin{array}{c} U\\ \tilde{C}_1 \end{array}\right]^{-1}\\ = \left[\begin{array}{c} \left[\begin{array}{cc} I_{n-p-r} & L^o \end{array}\right] \left[\begin{array}{cc} A_{22}^o & A_{122}^m \\ A_{21}^o & A_{22}^m \\ \end{array}\right]\\ \left[\begin{array}{cc} {K}_1 & {K}_2 \end{array}\right] \end{array}\right] \left[\begin{array}{cc} I_{n-p-r} & L^o\\ 0_{p-m\times n-p-r} & I_{p-m} \end{array}\right]^{-1}\\ = \left[\begin{array}{cc} A_{22}^o+L^oA_{21}^o & A_{122}^m+L^oA_{22}^m \\ {K}_1 & {K}_2 \end{array}\right] \left[\begin{array}{cc} I_{n-p-r} & -L^o\\ 0_{p-m\times n-p-r} & I_{p-m} \end{array}\right]\\ = \left[\begin{array}{cc} A_{22}^o+L^oA_{21}^o & A_{122}^m+L^oA_{22}^m-(A_{22}^o+L^oA_{21}^o)L^o \\ K_1 & K_2-K_1L^o \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0096b16ad8048d3787bdad7b1de35d39_l3.png)
ここで、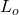 は
は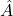 が安定行列となるように選んでおきます。また
が安定行列となるように選んでおきます。また
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \hat{J}=UA_{122}= \left[\begin{array}{cc} I_{n-p-r} & L^o \end{array}\right] \left[\begin{array}{cc} A_{1221} \\ A_{1222} \\ \end{array}\right] =A_{1221}+A_{1222}L^o }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ab3245bb625edb0bc7fb15b847f2cf26_l3.png)
以上を踏まえて、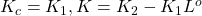 と選び、線形関数オブザーバを
と選び、線形関数オブザーバを
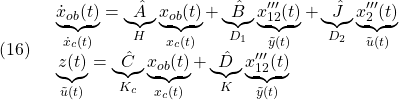
とみなせば、第2式を第1式に代入して
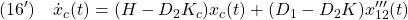
ただし
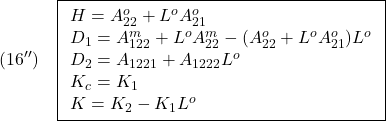
となって、補償器を得ていることになります。以下では、この補償器を用いたSM制御則の構成法について検討します。
[3] 制御対象の状態方程式と観測方程式は、それぞれ(18.1 )と(18.2
)と(18.2 )から次式で与えられます。
)から次式で与えられます。
![Rendered by QuickLaTeX.com \displaystyle{(17.1)\quad \begin{array}{l} \left[\begin{array}{c} \dot x'''_r(t)\\ \dot x'''_{11}(t)\\ \dot x'''_{12}(t)\\ \dot x'''_2(t) \end{array}\right]= \left[\begin{array}{ccccc} A_{11}^o & A_{12}^o & A_{121}^m & A_{121} \\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m & A_{1221} \\ 0_{p-m\times r} & A_{21}^o & A_{22}^m & A_{1222} \\ A_{211} & A_{212} & A_{213} & A_{22} \end{array}\right] \left[\begin{array}{c} x'''_r(t)\\ x'''_{11}(t)\\ x'''_{12}(t)\\ x'''_2(t) \end{array}\right]\\ + \left[\begin{array}{c} 0_{r\times m}\\ 0_{n-p-r\times m}\\ 0_{p-m\times m}\\ B_2\\ \end{array}\right] u(t)\\ (x'''_r(t)\in{\rm\bf R}^{r},x'''_{11}(t)\in{\rm\bf R}^{n-p-r},x'''_{12}(t)\in{\rm\bf R}^{p-m},x'''_{2}(t)\in{\rm\bf R}^{m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3e5a41c43ebb7a8d519dbce79ce8e0a3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(17.2)\quad \begin{array}{l} y(t) = \left[\begin{array}{cc} 0_{p\times n-p} & T \\ \end{array}\right] \left[\begin{array}{c} x'''_r(t)\\ x'''_{11}(t)\\ x'''_{12}(t)\\ x'''_2(t) \end{array}\right]=T \left[\begin{array}{c} x'''_{12}(t)\\ x'''_2(t) \end{array}\right] \quad(T\in{\rm\bf R}^{p\times p}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-354531fad73a9f4ed2fb9035460b7345_l3.png)
補償器は(16′)から次式で与えられます。
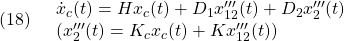
このとき補償器を合わせた制御対象のダイナミックスは次式のように表すことができます。
![Rendered by QuickLaTeX.com \displaystyle{(19.1)\quad \underbrace{ \left[\begin{array}{c} \dot z_r(t)\\ \dot x_c(t)\\ \dot x'''_{12}(t)\\ \dot x'''_2(t) \end{array}\right] }_{\hat x(t)} = \underbrace{ \left[\begin{array}{ccccc} A_{11}^o & A_{12}^o & A_{121}^m-A_{12}^oL^o & A_{121} \\ 0_{q\times r} & H & D_1 & D_2 \\ 0_{p-m\times r} & A_{21}^o & A_{22}^m-A_{21}^oL^o & A_{1222} \\ A_{211} & A_{212} & A_{213}-A_{212}L^o & A_{22} \end{array}\right] }_{\hat A} \underbrace{ \left[\begin{array}{c} z_r(t)\\ x_c(t)\\ x'''_{12}(t)\\ x'''_2(t) \end{array}\right] }_{\hat x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-661ada8558710f28b5c81d3d52ca8358_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ + \underbrace{ \left[\begin{array}{ccccc} 0_{r\times r} & 0_{r\times m} \\ 0_{q\times r} & 0_{q\times m} \\ 0_{p-m\times r} & A_{21}^o \\ A_{211} & A_{212} \end{array}\right] }_{\hat A_e} \underbrace{ \left[\begin{array}{c} e_r(t)\\ e_c(t) \end{array}\right] }_{\hat{e}(t)} + \underbrace{ \left[\begin{array}{c} 0_{r\times m}\\ 0_{q\times m}\\ 0_{p-m\times m}\\ B_2\\ \end{array}\right] }_{\hat B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-35bbf3c7686c6043f5322df182777814_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(19.2)\quad \underbrace{ \left[\begin{array}{c} \dot e_r(t)\\ \dot e_c(t) \end{array}\right] }_{\dot{\hat{e}}(t)} = \underbrace{ \left[\begin{array}{cc} A_{11}^o & A_{12}^o \\ 0 & H \end{array}\right] }_{\hat{H}} \underbrace{ \left[\begin{array}{c} e_r(t)\\ e_c(t) \end{array}\right] }_{\hat{e}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-eb43be95adf89038069e028493af823f_l3.png)
ここで、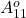 が安定行列であることは前提条件であり、また
が安定行列であることは前提条件であり、また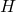 は安定行列となるようにオブザーバゲイン
は安定行列となるようにオブザーバゲイン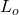 を決めます。
を決めます。
●(12)における推定誤差を
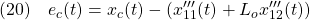
で定義します。補償器の状態方程式は
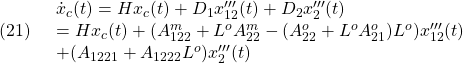
となることから、次式すなわち(19.2)の下段式を得ます。
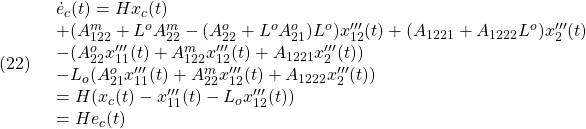
●(17.1)の第1式から
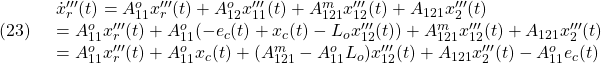
ここで、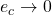 の場合の目標となるダイナミックスを次式で表します。
の場合の目標となるダイナミックスを次式で表します。
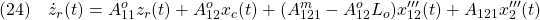
両者の状態の誤差を
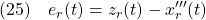
とすると、次式すなわち(19.2)の上段式を得ます。
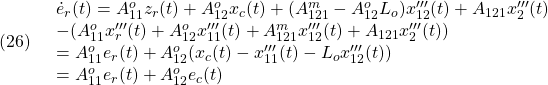
●(19.1)の第3式と第4式は、それぞれ(17.1)の第3式と第4式から次式のように得られます。
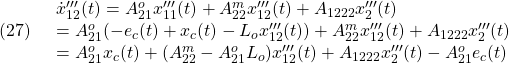
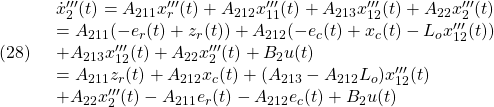
ちなみに(19.1)の第1式と第2式は、それぞれ(24)と(18)です。
●このときスイッチング関数(3′)は
![Rendered by QuickLaTeX.com \displaystyle{(3'')\quad \begin{array}{l} s(t)=Hx_c(t)+F_1C_1x'''_1(t)+F_2x'''_2(t)\\ =\boxed{\underbrace{F_2\left[\begin{array}{cccc} 0_{m\times r} & K_c & K & I_m \end{array}\right]}_{S}} \underbrace{ \left[\begin{array}{c} z_r(t)\\ x_c(t)\\ x'''_{12}(t)\\ x'''_2(t) \end{array}\right] }_{\hat x(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b40bb61a14d162099a8c5deefe1bb6ce_l3.png)
と表すことができます。
[4] 以上の準備のもとで、補償器によるSM制御則を次のように構築します。これは次のように線形制御部とスイッチング部からなります。
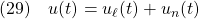
線形制御部を、SM標準形(19.1)に基づいて次式のように決めます。
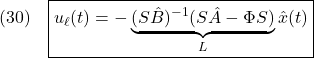
ここで、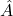 、
、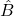 は(19.1)で定義されます。また
は(19.1)で定義されます。また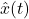 は、(17.2)より
は、(17.2)より
![Rendered by QuickLaTeX.com \displaystyle{(31)\quad \left[\begin{array}{c} x'''_{12}(t)\\ x'''_2(t) \end{array}\right] =T'y(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d42b58ac60227ff80d38187e30c6c7a1_l3.png)
と表せることに注意して、次の補償器の出力として得ます。
![Rendered by QuickLaTeX.com \displaystyle{(32)\quad \boxed{\begin{array}{l} \left[\begin{array}{c} \dot z_r(t)\\ \dot x_c(t) \end{array}\right] = \underbrace{ \left[\begin{array}{ccccc} A_{11}^o & A_{12}^o \\ 0_{q\times r} & H \end{array}\right] }_{\hat H} \left[\begin{array}{c} z_r(t)\\ x_c(t) \end{array}\right] + \underbrace{ \left[\begin{array}{ccccc} A_{121}^m-A_{12}^oL^o & A_{121} \\ D_1 & D_2 \end{array}\right]T' }_{\hat D} y(t)\\ \underbrace{ \left[\begin{array}{c} z_r(t)\\ x_c(t)\\ x'''_{12}(t)\\ x'''_2(t) \end{array}\right] }_{\hat x(t)}= \underbrace{ \left[\begin{array}{ccccc} I_r & 0_{r\times q}\\ 0_{q\times r} & I_q\\ 0_{p-m\times r} & 0_{p-m\times q} \\ 0_{m\times r} & 0_{m\times q} \\ \end{array}\right]}_{\widehat{\cal C}} \left[\begin{array}{c} z_r(t)\\ x_c(t) \end{array}\right] + \underbrace{\left[\begin{array}{ccccc} 0_{r\times p-m} & 0_{r\times m} \\ 0_{q\times p-m} & 0_{q\times m} \\ I_{p-m} & 0_{p-m\times m}\\ 0_{m\times p-m} & I_m \end{array}\right]T' }_{\widehat{\cal D}} y(t) \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-87e3ff7ce930f9ed16d07870318d8f43_l3.png)
スイッチング部を、次式のように決めます。
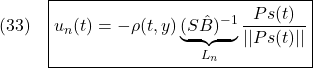
ここで、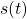 は(3”)で与えられます。また、
は(3”)で与えられます。また、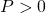 は適当な安定行列
は適当な安定行列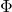 を与えて
を与えて
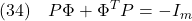
の解として求め、また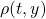 は
は
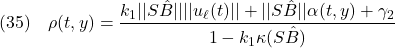
●以上に基づく設計手順を、数値例で示します。
| MATLAB |
%ex2_of_sm.m
%-----
clear all, close all
%(A,B,C)
A=[-2 1 0 0;
0 0 4 1;
0 1 0 0;
1 -6 -9 -2];
B=[0;0;0;1];
C=[0 0 1 0;
0 0 0 1];
[nn,mm]=size(B);
[pp,nn]=size(C);
%-----
[Af,Bf,Cf,r,Ta,Aa,Ba,Ca,Tb,T,Ac,Bc,Cc,Tc]=ca_form1(A,B,C)
%-----
%Assumes the triple (A,B,C) is in the canonical form of Lemma 5.3
%p1 is an nn-pp-r vector containing the desired poles of (A22o+Lo A21o)
%p2 is an nn-mm-r vector containing the desired poles of (A11tilde-A122 K)
%p3 is an mm vector representing the poles of the range space dynamics
A11o=Af(1:r,1:r);
A12o=Af(1:r,r+1:nn-pp);
A22o=Af(r+1:nn-pp,r+1:nn-pp);
A21o=Af(nn-pp+1:nn-mm,r+1:nn-pp);
A121m=Af(1:r,nn-pp+1:nn-mm);
A122m=Af(r+1:nn-pp,nn-pp+1:nn-mm);
A22m=Af(nn-pp+1:nn-mm,nn-pp+1:nn-mm);
A121=Af(1:r,nn-mm+1:nn);
A122=Af(r+1:nn-mm,nn-mm+1:nn);
A211=Af(nn-mm+1:nn,1:r);
A212=Af(nn-mm+1:nn,r+1:nn-pp);
A213=Af(nn-mm+1:nn,nn-pp+1:nn-mm);
A22=Af(nn-mm+1:nn,nn-mm+1:nn);
A11tilde=[A22o A122m;A21o A22m];
A1221=A122(1:nn-pp-r,:);
A1222=A122(nn-pp-r+1:nn-mm-r,:);
%-----
p1=-2.5
Lo=place(A22o',A21o',p1)
Lo=Lo';
%-----
p2=[-1,-1.5]
calK=place(A11tilde,A122,p2)
K1=calK(:,1:nn-pp-r)
K2=calK(:,nn-pp-r+1:nn-mm-r)
%-----
H=A22o+Lo*A21o
D1=A122m+Lo*A22m-H*Lo
D2=A1221+Lo*A1222
K=K2-K1*Lo
Kc=K1
Hhat=[A11o A12o;
zeros(nn-pp-r,r) H]
Dhat=[A121m-A12o*Lo A121;
D1 D2]*T'
%-----
S2=eye(mm);
S=S2*[zeros(mm,r) Kc K eye(mm)]
Ahat=[A11o A12o A121m-A12o*Lo A121;
zeros(nn-pp-r,r) H D1 D2;
zeros(pp-mm,r) A21o A22m-A21o*Lo A1222;
A211 A212 A213-A212*Lo A22]
p3=-5
Phi=diag(p3)
Lambda=S*Bf
L=-inv(Lambda)*S*Ahat+inv(Lambda)*Phi*S
P=lyap(Phi',eye(mm))
%-----
%eof
|

図1 補償器によるSM制御のシミュレーション例
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{(18.1^*)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x'''_1(t)\\ \dot x'''_2(t) \end{array}\right] }_{\dot{x}'''(t)} = \underbrace{ \left[\begin{array}{ccc|c} A_{11}^o & A_{12}^o & A_{121}^m & A_{121}\\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m & A_{1221}\\ 0_{p-m\times r} & A_{21}^o & A_{22}^m & A_{1222}\\\hline A_{2120} & A_{2121} & A_{2122} & A_{22} \end{array}\right] }_{(T_aT_bT_c)A(T_aT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] }_{x'''(t)}\\ + \underbrace{ \left[\begin{array}{c} 0_{r\times m} \\ 0_{n-p-r\times m} \\ 0_{p-m\times m} \\\hline B_2 \end{array}\right] }_ {(T_aT_bT_c)B} \underbrace{(u(t)+\xi(t,x,u))}_{u'(t)}\\ (A_{11}^o\in{\rm\bf R}^{r\times r},A_{22}^o\in{\rm\bf R}^{n-p-r\times n-p-r},A_{22}^m\in{\rm\bf R}^{p-m\times p-m},A_{22}\in{\rm\bf R}^{m\times m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-712c9ee206bbfdfc0320ee7fb2c01281_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(18.2^*)\quad \begin{array}{l} y(t) = \underbrace{ \left[\begin{array}{cc} 0_{p\times n-p} & T \\ \end{array}\right] }_{C(T_aT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] }_{x'''(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c2d502c3e8c7b30de092731cc5418e3d_l3.png)
![]() とおくと
とおくと![Rendered by QuickLaTeX.com \displaystyle{(2')\quad \begin{array}{l} \dot{x}_c(t)=Hx_c(t)+Dy(t)\\ =Hx_c(t)+ \left[\begin{array}{cc} 0_{p\times n-p} & DT \\ \end{array}\right] %\underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] %}_{x'''(t)} \\ =Hx_c(t)+ \left[\begin{array}{cc} D_1C_1 & D_2 \\ \end{array}\right] %\underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] %}_{x'''(t)} \\ =Hx_c(t)+D_1C_1x'''_1(t)+D_2x'''_2(t)\\ (DT=\left[\begin{array}{cc} D_1 & D_2 \end{array}\right], D_1\in{\rm\bf R}^{m\times p-m}, D_2\in{\rm\bf R}^{m\times m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9c519f23b2642a1398b44d297648888d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3')\quad \begin{array}{l} s(t)=F_cx_c(t)+Fy(t)\\ =Hx_c(t)+ \left[\begin{array}{cc} 0_{p\times n-p} & FT \\ \end{array}\right] %\underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] %}_{x'''(t)} \\ =Hx_c(t)+ \left[\begin{array}{cc} F_1C_1 & F_2 \\ \end{array}\right] %\underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] %}_{x'''(t)} \\ =Hx_c(t)+F_1C_1x'''_1(t)+F_2x'''_2(t)\\ (FT=\left[\begin{array}{cc} F_1 & F_2 \end{array}\right], F_1\in{\rm\bf R}^{m\times p-m}, F_2\in{\rm\bf R}^{m\times m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c3a63f48d662d8ce45ee20bfb786b893_l3.png)
![]() )と(2′)を結合し、
)と(2′)を結合し、![]() を用いて、次式を得ます。
を用いて、次式を得ます。![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x'''_1(t)\\\hline \dot x'''_2(t)\\\hline\hline \dot x_c(t) \end{array}\right] }_{\dot{x}'''(t)} = \left[\begin{array}{c|c||c} \left.\begin{array}{ccc} A_{11}^o & A_{12}^o & A_{121}^m \\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m \\ 0_{p-m\times r} & A_{21}^o & A_{22}^m \\ \end{array}\right.& \left.\begin{array}{cc} A_{121}\\ A_{1221}\\ A_{1222} \end{array}\right.& \left.\begin{array}{cc} 0_{r\times q} \\ 0_{n-p-r\times q} \\ 0_{p-m\times q} \end{array}\right. \\\hline \left.\begin{array}{ccc} A_{211} & A_{2121} &A_{2122} \end{array}\right.& \left.\begin{array}{cc} A_{22} \end{array}\right.& 0_{m\times q} \\\hline\hline %D_1C_1 \left.\begin{array}{cc} 0_{q\times r} & D_1\tilde{C}_1 \end{array}\right. & D_2 & H \end{array}\right]\\ \times \underbrace{ \left[\begin{array}{c} x'''_1(t)\\\hline x'''_2(t)\\\hline\hline x_c(t) \end{array}\right] }_{x'''(t)} + \left[\begin{array}{c} 0_{r\times m} \\ 0_{n-p-r\times m} \\ 0_{p-m\times m} \\\hline B_2\\\hline\hline 0_{q\times m} \end{array}\right] u'(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1968121e3a5d1a000f172ea9ce55a016_l3.png)
![]() と
と![]() を入れ替えて
を入れ替えて![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x'''_1(t)\\\hline \dot x_c(t)\\\hline\hline \dot x'''_2(t) \end{array}\right] }_{\dot{x}'''(t)} = \left[\begin{array}{c|c||c} \left.\begin{array}{ccc} A_{11}^o & A_{12}^o & A_{121}^m \\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m \\ 0_{p-m\times r} & A_{21}^o & A_{22}^m \\ \end{array}\right.& \left.\begin{array}{cc} 0_{r\times q} \\ 0_{n-p-r\times q} \\ 0_{p-m\times q} \end{array}\right. & \left.\begin{array}{cc} A_{121}\\ A_{1221}\\ A_{1222} \end{array}\right. \\\hline %D_1C_1 \left.\begin{array}{ccc} 0_{q\times r} & D_1\tilde{C}_1 \end{array}\right. & \left.\begin{array}{cc} H \end{array}\right. & D_2 \\\hline\hline \left.\begin{array}{ccc} A_{211} & A_{2121} &A_{2122} \end{array}\right. & 0_{m\times q} & A_{22} \end{array}\right]\\ \times \underbrace{ \left[\begin{array}{c} x'''_1(t)\\\hline x_c(t)\\\hline\hline x'''_2(t) \end{array}\right] }_{x'''(t)} + \left[\begin{array}{c} 0_{r\times m} \\ 0_{n-p-r\times m} \\ 0_{p-m\times m} \\\hline 0_{q\times m}\\\hline\hline B_2\\ \end{array}\right] u'(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-954b2e74e37e5828afcfbe39a920d5cb_l3.png)
![]() を
を![]() 、
、![]() 、
、![]() に分割し、座標変換
に分割し、座標変換![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} x'''_r(t)\\ x'''_{11}(t)\\ x'''_{12}(t)\\\hline x_c(t)\\\hline\hline x''''_2(t)\\ \end{array}\right] }_{x''''(t)} = \underbrace{ \left[\begin{array}{ccc|c||c} I_{r} & 0 & 0 & 0& 0 \\ 0 & I_{n-p-r} & 0 & 0& 0 \\ 0 & 0 & I_{p-m} & 0 & 0\\\hline 0 & 0 & 0 & I_q &0 \\\hline\hline 0 & 0 & K & K_c & I_m \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x'''_r(t)\\ x'''_{11}(t)\\ x'''_{12}(t)\\\hline x_c(t)\\\hline\hline x'''_2(t)\\ \end{array}\right] }_{x'''(t)}\\ (K=F_2^{-1}F_1, K_c=F_2^{-1}F_c) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bb2718c0970f9bbdf8747a901f89c9ab_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x'''_r(t)\\ \dot x'''_{11}(t)\\ \dot x'''_{12}(t)\\\hline \dot x_c(t)\\\hline \dot x''''_2(t) \end{array}\right] }_{\dot{x}''''(t)} = \left[\begin{array}{c|c} \left[\begin{array}{c|c} \left.\begin{array}{ccc} A_{11}^o & A_{12}^o & A_{121}^m \\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m \\ 0_{p-m\times r} & A_{21}^o & A_{22}^m \\ \end{array}\right. & \left.\begin{array}{cc} 0_{r\times q} \\ 0_{n-p-r\times q} \\ 0_{p-m\times q} \end{array}\right. \\\hline %D_1C_1 \left.\begin{array}{cc} 0_{q\times r} & D_1\tilde{C}_1 \end{array}\right. & H \end{array}\right]\\ - \left[\begin{array}{cc} A_{121}\\ A_{1221}\\ A_{1222}\\\hline D_2 \end{array}\right] \left[\begin{array}{ccccc} 0_{m\times r} & K\tilde{C}_1 & K_c \end{array}\right] & \left.\begin{array}{cc} A_{121}\\ A_{1221}\\ A_{1222}\\\hline D_2 \end{array}\right. \\\hline \left.\begin{array}{ccc|c} A_{211} & A_{2121} &A_{2122} & 0_{m\times q} \end{array}\right. & A_{22} \end{array}\right]\\ \times \underbrace{ \left[\begin{array}{c} x'''_r(t)\\ x'''_{11}(t)\\ x'''_{12}(t)\\\hline x_c(t)\\\hline x''''_2(t)\\ \end{array}\right] }_{x''''(t)} + \left[\begin{array}{c} 0_{r\times m} \\ 0_{n-p-r\times m} \\ 0_{p-m\times m} \\\hline 0_{q\times m}\\\hline B_2 \end{array}\right] u'(t)\\ = \underbrace{ \left[\begin{array}{c|c} \left.\begin{array}{c|c} \left.\begin{array}{ccc} A_{11}^o & A_{12}^o & A_{121}^m-A_{121}K \\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m-A_{1221}K \\ 0_{p-m\times r} & A_{21}^o & A_{22}^m-A_{1222}K \end{array}\right. & \left.\begin{array}{cc} -A_{121}K_c\\ -A_{1221}K_c\\ -A_{1222}K_c\\ \end{array}\right. \\\hline %(D_1-D_2K)C_1 \left.\begin{array}{cc} 0_{q\times r} & D(D_1-D_2K)\tilde{C}_1 \end{array}\right. & H-D_2K_c \end{array}\right. & \left.\begin{array}{cc} A_{121}\\ A_{1221}\\ A_{1222}\\\hline D_2 \end{array}\right.\\\hline \left.\begin{array}{ccc|c} A_{211} & A_{2121} &A_{2122} & 0_{m\times q} \end{array}\right. & A_{22} \end{array}\right] }_{ \left[\begin{array}{cc} \tilde{\cal A}_{11} & \tilde{\cal A}_{12} \\ \tilde{\cal A}_{21} & \tilde{\cal A}_{22} \end{array}\right]} \\ \times \underbrace{ \left[\begin{array}{c} x'''_r(t)\\ x'''_{11}(t)\\ x'''_{12}(t)\\\hline x_c(t)\\\hline x''''_2(t)\\ \end{array}\right] }_{x''''(t)} + \left[\begin{array}{c} 0_{r\times m} \\ 0_{n-p-r\times m} \\ 0_{p-m\times m} \\\hline 0_{q\times m}\\\hline B_2 \end{array}\right] u'(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1a787fcbba242095e1c00febe98dcfe6_l3.png)
![]() が安定行列であることを前提として、
が安定行列であることを前提として、![]() を安定行列とする
を安定行列とする![]() を求めます。
を求めます。![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \left[\begin{array}{c} \dot x'''_{11}(t)\\ \dot x'''_{12}(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} A_{22}^o & A_{122}^m \\ A_{21}^o & A_{22}^m \\ \end{array}\right] }_{\tilde{A}_{11}} \left[\begin{array}{c} x'''_{11}(t)\\ x'''_{12}(t) \end{array}\right] + \underbrace{ \left[\begin{array}{cc} A_{1221} \\ A_{1222} \\ \end{array}\right] }_{A_{122}} \underbrace{x'''_{2}(t)}_{\tilde u(t)} \\ \underbrace{x'''_{12}(t)}_{\tilde y(t)} = \underbrace{ \left[\begin{array}{cc} 0_{p-m\times n-p-r} & I_{p-m} \end{array}\right] }_{\tilde{C}_1}} \left[\begin{array}{c} x'''_{11}(t)\\ x'''_{12}(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0a20a7d2962db1ada4badc2bf0778a94_l3.png)
![]()
![]() のすべての要素は観測できないので、関数オブザーバ
のすべての要素は観測できないので、関数オブザーバ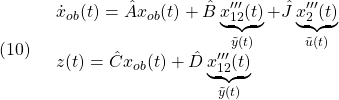
![]() に安定化状態フィードバック則
に安定化状態フィードバック則![]() を推定させます。すなわち
を推定させます。すなわち![]()
![]() も適当な状態の線形関数を推定する必要があり、これを次のように表します。
も適当な状態の線形関数を推定する必要があり、これを次のように表します。![Rendered by QuickLaTeX.com \displaystyle{(12)\quad x_{ob}(t)\rightarrow \underbrace{ \left[\begin{array}{cc} I_{n-p-r} & -L^o \end{array}\right] }_{U} \left[\begin{array}{c} x'''_{11}(t)\\ x'''_{12}(t) \end{array}\right]= x'''_{11}(t)-L^ox'''_{12}(t) \quad(t\rightarrow\infty) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7c76952731eb4799d0b3b24379431e11_l3.png)
![]() を適当に与えたとき、関数オブザーバのパラメータは
を適当に与えたとき、関数オブザーバのパラメータは![]()
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \begin{array}{l} \left[\begin{array}{cc} \hat{A} & \hat{B}\\ \hat{C} & \hat{D} \end{array}\right] = \left[\begin{array}{c} U\tilde{A}_{11}\\ \left[\begin{array}{cc} {K}_1 & {K}_2 \end{array}\right] \end{array}\right] \left[\begin{array}{c} U\\ \tilde{C}_1 \end{array}\right]^{-1}\\ = \left[\begin{array}{c} \left[\begin{array}{cc} I_{n-p-r} & L^o \end{array}\right] \left[\begin{array}{cc} A_{22}^o & A_{122}^m \\ A_{21}^o & A_{22}^m \\ \end{array}\right]\\ \left[\begin{array}{cc} {K}_1 & {K}_2 \end{array}\right] \end{array}\right] \left[\begin{array}{cc} I_{n-p-r} & L^o\\ 0_{p-m\times n-p-r} & I_{p-m} \end{array}\right]^{-1}\\ = \left[\begin{array}{cc} A_{22}^o+L^oA_{21}^o & A_{122}^m+L^oA_{22}^m \\ {K}_1 & {K}_2 \end{array}\right] \left[\begin{array}{cc} I_{n-p-r} & -L^o\\ 0_{p-m\times n-p-r} & I_{p-m} \end{array}\right]\\ = \left[\begin{array}{cc} A_{22}^o+L^oA_{21}^o & A_{122}^m+L^oA_{22}^m-(A_{22}^o+L^oA_{21}^o)L^o \\ K_1 & K_2-K_1L^o \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0096b16ad8048d3787bdad7b1de35d39_l3.png)
![]() は
は![]() が安定行列となるように選んでおきます。また
が安定行列となるように選んでおきます。また![]()
![]() と選び、線形関数オブザーバを
と選び、線形関数オブザーバを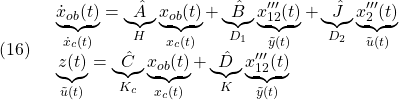
![]()
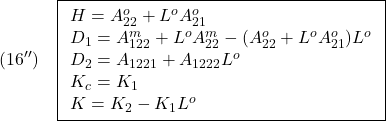
![]() )と(18.2
)と(18.2![]() )から次式で与えられます。
)から次式で与えられます。![Rendered by QuickLaTeX.com \displaystyle{(17.1)\quad \begin{array}{l} \left[\begin{array}{c} \dot x'''_r(t)\\ \dot x'''_{11}(t)\\ \dot x'''_{12}(t)\\ \dot x'''_2(t) \end{array}\right]= \left[\begin{array}{ccccc} A_{11}^o & A_{12}^o & A_{121}^m & A_{121} \\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m & A_{1221} \\ 0_{p-m\times r} & A_{21}^o & A_{22}^m & A_{1222} \\ A_{211} & A_{212} & A_{213} & A_{22} \end{array}\right] \left[\begin{array}{c} x'''_r(t)\\ x'''_{11}(t)\\ x'''_{12}(t)\\ x'''_2(t) \end{array}\right]\\ + \left[\begin{array}{c} 0_{r\times m}\\ 0_{n-p-r\times m}\\ 0_{p-m\times m}\\ B_2\\ \end{array}\right] u(t)\\ (x'''_r(t)\in{\rm\bf R}^{r},x'''_{11}(t)\in{\rm\bf R}^{n-p-r},x'''_{12}(t)\in{\rm\bf R}^{p-m},x'''_{2}(t)\in{\rm\bf R}^{m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3e5a41c43ebb7a8d519dbce79ce8e0a3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(17.2)\quad \begin{array}{l} y(t) = \left[\begin{array}{cc} 0_{p\times n-p} & T \\ \end{array}\right] \left[\begin{array}{c} x'''_r(t)\\ x'''_{11}(t)\\ x'''_{12}(t)\\ x'''_2(t) \end{array}\right]=T \left[\begin{array}{c} x'''_{12}(t)\\ x'''_2(t) \end{array}\right] \quad(T\in{\rm\bf R}^{p\times p}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-354531fad73a9f4ed2fb9035460b7345_l3.png)
![]()
![Rendered by QuickLaTeX.com \displaystyle{(19.1)\quad \underbrace{ \left[\begin{array}{c} \dot z_r(t)\\ \dot x_c(t)\\ \dot x'''_{12}(t)\\ \dot x'''_2(t) \end{array}\right] }_{\hat x(t)} = \underbrace{ \left[\begin{array}{ccccc} A_{11}^o & A_{12}^o & A_{121}^m-A_{12}^oL^o & A_{121} \\ 0_{q\times r} & H & D_1 & D_2 \\ 0_{p-m\times r} & A_{21}^o & A_{22}^m-A_{21}^oL^o & A_{1222} \\ A_{211} & A_{212} & A_{213}-A_{212}L^o & A_{22} \end{array}\right] }_{\hat A} \underbrace{ \left[\begin{array}{c} z_r(t)\\ x_c(t)\\ x'''_{12}(t)\\ x'''_2(t) \end{array}\right] }_{\hat x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-661ada8558710f28b5c81d3d52ca8358_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ + \underbrace{ \left[\begin{array}{ccccc} 0_{r\times r} & 0_{r\times m} \\ 0_{q\times r} & 0_{q\times m} \\ 0_{p-m\times r} & A_{21}^o \\ A_{211} & A_{212} \end{array}\right] }_{\hat A_e} \underbrace{ \left[\begin{array}{c} e_r(t)\\ e_c(t) \end{array}\right] }_{\hat{e}(t)} + \underbrace{ \left[\begin{array}{c} 0_{r\times m}\\ 0_{q\times m}\\ 0_{p-m\times m}\\ B_2\\ \end{array}\right] }_{\hat B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-35bbf3c7686c6043f5322df182777814_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(19.2)\quad \underbrace{ \left[\begin{array}{c} \dot e_r(t)\\ \dot e_c(t) \end{array}\right] }_{\dot{\hat{e}}(t)} = \underbrace{ \left[\begin{array}{cc} A_{11}^o & A_{12}^o \\ 0 & H \end{array}\right] }_{\hat{H}} \underbrace{ \left[\begin{array}{c} e_r(t)\\ e_c(t) \end{array}\right] }_{\hat{e}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-eb43be95adf89038069e028493af823f_l3.png)
![]() が安定行列であることは前提条件であり、また
が安定行列であることは前提条件であり、また![]() は安定行列となるようにオブザーバゲイン
は安定行列となるようにオブザーバゲイン![]() を決めます。
を決めます。![]()
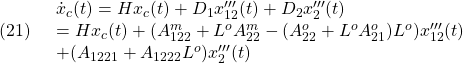
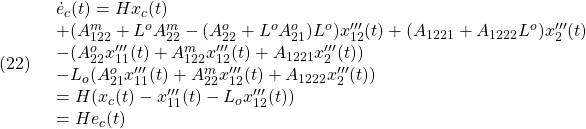
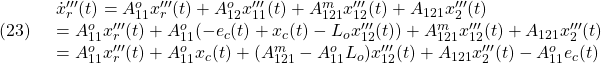
![]() の場合の目標となるダイナミックスを次式で表します。
の場合の目標となるダイナミックスを次式で表します。![]()
![]()
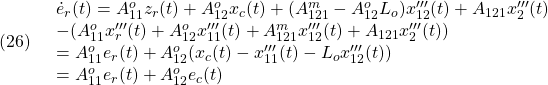
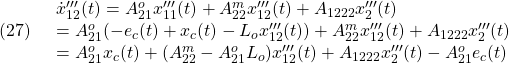
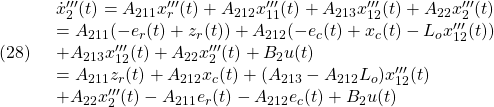
![Rendered by QuickLaTeX.com \displaystyle{(3'')\quad \begin{array}{l} s(t)=Hx_c(t)+F_1C_1x'''_1(t)+F_2x'''_2(t)\\ =\boxed{\underbrace{F_2\left[\begin{array}{cccc} 0_{m\times r} & K_c & K & I_m \end{array}\right]}_{S}} \underbrace{ \left[\begin{array}{c} z_r(t)\\ x_c(t)\\ x'''_{12}(t)\\ x'''_2(t) \end{array}\right] }_{\hat x(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b40bb61a14d162099a8c5deefe1bb6ce_l3.png)
![]()
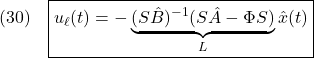
![]() 、
、![]() は(19.1)で定義されます。また
は(19.1)で定義されます。また![]() は、(17.2)より
は、(17.2)より![]()
![Rendered by QuickLaTeX.com \displaystyle{(32)\quad \boxed{\begin{array}{l} \left[\begin{array}{c} \dot z_r(t)\\ \dot x_c(t) \end{array}\right] = \underbrace{ \left[\begin{array}{ccccc} A_{11}^o & A_{12}^o \\ 0_{q\times r} & H \end{array}\right] }_{\hat H} \left[\begin{array}{c} z_r(t)\\ x_c(t) \end{array}\right] + \underbrace{ \left[\begin{array}{ccccc} A_{121}^m-A_{12}^oL^o & A_{121} \\ D_1 & D_2 \end{array}\right]T' }_{\hat D} y(t)\\ \underbrace{ \left[\begin{array}{c} z_r(t)\\ x_c(t)\\ x'''_{12}(t)\\ x'''_2(t) \end{array}\right] }_{\hat x(t)}= \underbrace{ \left[\begin{array}{ccccc} I_r & 0_{r\times q}\\ 0_{q\times r} & I_q\\ 0_{p-m\times r} & 0_{p-m\times q} \\ 0_{m\times r} & 0_{m\times q} \\ \end{array}\right]}_{\widehat{\cal C}} \left[\begin{array}{c} z_r(t)\\ x_c(t) \end{array}\right] + \underbrace{\left[\begin{array}{ccccc} 0_{r\times p-m} & 0_{r\times m} \\ 0_{q\times p-m} & 0_{q\times m} \\ I_{p-m} & 0_{p-m\times m}\\ 0_{m\times p-m} & I_m \end{array}\right]T' }_{\widehat{\cal D}} y(t) \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-87e3ff7ce930f9ed16d07870318d8f43_l3.png)
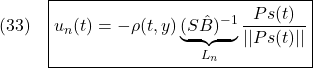
![]() は(3”)で与えられます。また、
は(3”)で与えられます。また、![]() は適当な安定行列
は適当な安定行列![]() を与えて
を与えて![]()
![]() は
は![]()
