| MATLAB |
%cACCBP_of_gs.m
%-----
clear all, close all
m1=1; m2=1; kmin=0.5; kmax=2;
A1=[0 0 1 0;0 0 0 1;-kmin/m1 kmin/m1 0 0;kmin/m2 -kmin/m2 0 0];
A2=[0 0 1 0;0 0 0 1;-kmax/m1 kmax/m1 0 0;kmax/m2 -kmax/m2 0 0];
BG=[0 0 0;0 0 0;1/m1 0 1/m1;0 1/m2 0];
B1=BG(:,2); B2=BG(:,3);
C1=[-1 1 0 0;1 0 0 0;0 0 0 0]; D11=zeros(3,1); D12=[0;0;2];
C2=[1 0 0 0]; D21=0; D22=0;
%-----
alpha=0.05; r=5; th=0.5*pi;
LMIs=of_synlmi7(A1,A2,B1,B2,C1,C2,D11,D12,D21,D22,alpha,r,th);
cobj=zeros(1,decnbr(LMIs));
cobj(1)=1;
[cost,xopt]=mincx(LMIs,cobj);
gopt=dec2mat(LMIs,xopt,1)
R=dec2mat(LMIs,xopt,2);
S=dec2mat(LMIs,xopt,3);
%-----
ak1=dec2mat(LMIs,xopt,4);
bk1=dec2mat(LMIs,xopt,5);
ck1=dec2mat(LMIs,xopt,6);
dk1=dec2mat(LMIs,xopt,7);
[u,sd,v]=svd(eye(size(A1,1))-R*S);
sd=diag(sqrt(1./diag(sd)));
Ni=sd*v'; Mti=u*sd;
AK1=Ni*(ak1-S*(A1-B2*dk1*C2)*R-bk1*C2*R-S*B2*ck1)*Mti;
BK1=Ni*(bk1-S*B2*dk1);
CK1=(ck1-dk1*C2*R)*Mti;
DK1=dk1;
K1=[AK1 BK1;CK1 DK1];
%-----
ak2=dec2mat(LMIs,xopt,8);
bk2=dec2mat(LMIs,xopt,9);
ck2=dec2mat(LMIs,xopt,10);
dk2=dec2mat(LMIs,xopt,11);
[u,sd,v]=svd(eye(size(A2,1))-R*S);
sd=diag(sqrt(1./diag(sd)));
Ni=sd*v'; Mti=u*sd;
AK2=Ni*(ak2-S*(A2-B2*dk2*C2)*R-bk2*C2*R-S*B2*ck2)*Mti;
BK2=Ni*(bk2-S*B2*dk2);
CK2=(ck2-dk2*C2*R)*Mti;
DK2=dk2;
K2=[AK2 BK2;CK2 DK2];
%-----
A0=[0 0 1 0;0 0 0 1;0 0 0 0;0 0 0 0];
A1=[0 0 0 0;0 0 0 0;-1/m1 1/m1 0 0;1/m2 -1/m2 0 0];
prange=kmax-kmin; pmax=kmax; pmin=kmin;
t0=0; t1=20; t=t0:(t1-t0)/100:t1;
for i=1:100
k=rand*(kmax-kmin)+kmin;
A=A0+k*A1;
p1=(pmax-k)/prange; p2=(k-pmin)/prange;
AK=p1*AK1+p2*AK2;
BK=p1*BK1+p2*BK2;
CK=p1*CK1+p2*CK2;
DK=p1*DK1+p2*DK2;
ACL=[A+B2*DK*C2 B2*CK;BK*C2 AK];
BCL=[B1+B2*DK*D21;BK*D21];
CCL=[1 0 0]*[C1+D12*DK*C2 D12*CK];
DCL=[1 0 0]*(D11+D12*DK*D21);
sys=ss(ACL,BCL,CCL,DCL);
[y,t]=initial(sys,[B1;zeros(4,1)],t);
figure(1),plot(t,y),hold on
end
axis([t0 t1 -2 2]),grid
%-----
function LMIs=of_synlmi7(A1,A2,B1,B2,C1,C2,D11,D12,D21,D22,alpha,r,th)
[n,m]=size(B2); [p,n]=size(C2);
setlmis([]);
gam=lmivar(1,[1 0]);
[R,xxx,Rdec]=lmivar(1,[n 1]);
[S,xxx,Sdec]=lmivar(1,[n 1]);
Ak1=lmivar(2,[n n]);
Bk1=lmivar(2,[n p]);
Ck1=lmivar(2,[m n]);
Dk1=lmivar(2,[m p]);
Ak2=lmivar(2,[n n]);
Bk2=lmivar(2,[n p]);
Ck2=lmivar(2,[m n]);
Dk2=lmivar(2,[m p]);
%=====
lmiRS1=newlmi;
lmiterm([lmiRS1 1 1 R],A1,1,'s'); %#1:R*A'+AR
lmiterm([lmiRS1 1 1 Ck1],B2,1,'s'); %#1:Ck'*B2'+B2*Ck
lmiterm([lmiRS1 2 1 0],A1'); %#1:A'
lmiterm([lmiRS1 2 1 Ak1],1,1); %#1:Ak
lmiterm([lmiRS1 2 1 -Dk1],C2',B2'); %#1:C2'*Dk'*B2'
lmiterm([lmiRS1 2 2 S],1,A1,'s'); %#1:A'*S+S*A
lmiterm([lmiRS1 2 2 Bk1],1,C2,'s'); %#1:C2'*Bk'+Bk*C2
lmiterm([lmiRS1 1 3 0],B1); %#1:B1
lmiterm([lmiRS1 1 3 Dk1],B2,D21); %#1:B2*Dk*D21
lmiterm([lmiRS1 2 3 S],1,B1); %#1:S*B1
lmiterm([lmiRS1 2 3 Bk1],1,D21); %#1:Bk*D21
lmiterm([lmiRS1 3 3 gam],-1,1); %#1:-gam
lmiterm([lmiRS1 4 1 R],C1,1); %#1:C1*R
lmiterm([lmiRS1 4 1 Ck1],D12,1); %#1:D12*Ck
lmiterm([lmiRS1 4 2 0],C1); %#1:C1
lmiterm([lmiRS1 4 2 Dk1],D12,C2); %#1:D12*Dk*C2
lmiterm([lmiRS1 4 3 0],D11); %#1:D11
lmiterm([lmiRS1 4 3 Dk1],D12,D21); %#1:D12*Dk*D21
lmiterm([lmiRS1 4 4 gam],-1,1); %#1:-gam
%-----
lmiPL11=newlmi;
lmiterm([lmiPL11 1 1 R],A1,1,'s'); %#2:R*A'+A*R
lmiterm([lmiPL11 1 1 Ck1],B2,1,'s'); %#2:Ck'*B2'+B2*Ck
lmiterm([lmiPL11 2 1 Ak1],1,1); %#2:Ak
lmiterm([lmiPL11 1 2 0],A1); %#2:A
lmiterm([lmiPL11 1 2 Dk1],B2,C2); %#2:B2*Dk*C2
lmiterm([lmiPL11 2 2 S],1,A1,'s'); %#2:A'*S+S*A
lmiterm([lmiPL11 2 2 Bk1],1,C2,'s'); %#2:C2'*Bk'+Bk*C2
%
lmiterm([lmiPL11 1 1 R],2*alpha,1); %#2:2*alpha*R
lmiterm([lmiPL11 2 1 0],2*alpha); %#2:2*alpha*I
lmiterm([lmiPL11 2 2 S],2*alpha,1); %#2:2*alpha*S
%-----
lmiPL21=newlmi;
lmiterm([lmiPL21 1 1 R],-r,1); %#3:-r*R
lmiterm([lmiPL21 2 1 0],-r); %#3:-r*I
lmiterm([lmiPL21 2 2 S],-r,1); %#3:-r*S
%
lmiterm([lmiPL21 1 3 R],A1,1); %#3:A*R
lmiterm([lmiPL21 1 3 Ck1],B2,1); %#3:B2*Ck
lmiterm([lmiPL21 2 3 Ak1],1,1); %#3:Ak
lmiterm([lmiPL21 1 4 0],A1); %#3:A
lmiterm([lmiPL21 1 4 Dk1],B2,C2); %#3:B2*Dk*C2
lmiterm([lmiPL21 2 4 S],1,A1); %#3:S*A
lmiterm([lmiPL21 2 4 Bk1],1,C2); %#3:Bk*C2
%
lmiterm([lmiPL21 3 3 R],-r,1); %#3:-r*R
lmiterm([lmiPL21 4 3 0],-r); %#3:-r*I
lmiterm([lmiPL21 4 4 S],-r,1); %#3:-r*S
%-----
sth=sin(th); cth=cos(th);
lmiPL31=newlmi;
lmiterm([lmiPL31 1 1 R],sth*A1,1,'s'); %#4:sth*(R*A'+A*R)
lmiterm([lmiPL31 1 1 Ck1],sth*B2,1,'s');%#4:sth*(Ck'*B2'+B2*Ck)
lmiterm([lmiPL31 2 1 Ak1],sth,1); %#4:sth*(Ak)
lmiterm([lmiPL31 1 2 0],sth*A1); %#4:sth*(A)
lmiterm([lmiPL31 1 2 Dk1],sth*B2,C2); %#4:sth*(B2*Dk*C2)
lmiterm([lmiPL31 2 2 S],1,sth*A1,'s'); %#4:sth*(A'*S+S*A)
lmiterm([lmiPL31 2 2 Bk1],1,sth*C2,'s');%#4:sth*(C2'*Bk'+Bk*C2)
%
lmiterm([lmiPL31 1 3 R],cth*A1,1); %#1:cth*(A*R)
lmiterm([lmiPL31 1 3 R],1,-cth*A1'); %#1:cth*(-R*A')
lmiterm([lmiPL31 1 3 Ck1],cth*B2,1); %#1:cth*(B*Ck)
lmiterm([lmiPL31 1 3 -Ck1],-cth*B2',1); %#1:cth*(-Ck'*B')
lmiterm([lmiPL31 2 3 Ak1],cth,1); %#4:cth*(Ak)
lmiterm([lmiPL31 1 4 -Ak1],-cth,1); %#4:cth*(-Ak')
lmiterm([lmiPL31 1 4 0],A1); %#4:cth*(A)
lmiterm([lmiPL31 2 3 0],-A1'); %#4:cth*(-A')
lmiterm([lmiPL31 1 4 Dk1],cth*B2,C2); %#4:cth*(B2*Dk*C2)
lmiterm([lmiPL31 2 3 -Dk1],-cth*C2',B2');%#4:cth*(-C2'*Dk'*B2')
lmiterm([lmiPL31 2 4 S],1,cth*A1); %#4:cth*(S*A)
lmiterm([lmiPL31 2 4 S],-cth*A1',1); %#4:cth*(-A'*S)
lmiterm([lmiPL31 2 4 Bk1],1,cth*C2); %#4:cth*(Bk*C2)
lmiterm([lmiPL31 2 4 -Bk1],-cth*C2',1); %#4:cth*(-C2'*Bk')
%
lmiterm([lmiPL31 3 3 R],sth*A1,1,'s'); %#4:sth*(R*A'+A*R)
lmiterm([lmiPL31 3 3 Ck1],sth*B2,1,'s');%#4:sth*(Ck'*B2'+B2*Ck)
lmiterm([lmiPL31 4 3 Ak1],sth,1); %#4:sth*(Ak)
lmiterm([lmiPL31 3 4 0],sth*A1); %#4:sth*(A)
lmiterm([lmiPL31 3 4 Dk1],sth*B2,C2); %#4:sth*(B2*Dk*C2)
lmiterm([lmiPL31 4 4 S],1,sth*A1,'s'); %#4:sth*(A'*S+S*A)
lmiterm([lmiPL31 4 4 Bk1],1,sth*C2,'s');%#4:sth*(C2'*Bk'+Bk*C2)
%=====
lmiRS2=newlmi;
lmiterm([lmiRS2 1 1 R],A2,1,'s'); %#1:R*A'+AR
lmiterm([lmiRS2 1 1 Ck2],B2,1,'s'); %#1:Ck'*B2'+B2*Ck
lmiterm([lmiRS2 2 1 0],A2'); %#1:A'
lmiterm([lmiRS2 2 1 Ak2],1,1); %#1:Ak
lmiterm([lmiRS2 2 1 -Dk2],C2',B2'); %#1:C2'*Dk'*B2'
lmiterm([lmiRS2 2 2 S],1,A2,'s'); %#1:A'*S+S*A
lmiterm([lmiRS2 2 2 Bk2],1,C2,'s'); %#1:C2'*Bk'+Bk*C2
lmiterm([lmiRS2 1 3 0],B1); %#1:B1
lmiterm([lmiRS2 1 3 Dk2],B2,D21); %#1:B2*Dk*D21
lmiterm([lmiRS2 2 3 S],1,B1); %#1:S*B1
lmiterm([lmiRS2 2 3 Bk2],1,D21); %#1:Bk*D21
lmiterm([lmiRS2 3 3 gam],-1,1); %#1:-gam
lmiterm([lmiRS2 4 1 R],C1,1); %#1:C1*R
lmiterm([lmiRS2 4 1 Ck2],D12,1); %#1:D12*Ck
lmiterm([lmiRS2 4 2 0],C1); %#1:C1
lmiterm([lmiRS2 4 2 Dk2],D12,C2); %#1:D12*Dk*C2
lmiterm([lmiRS2 4 3 0],D11); %#1:D11
lmiterm([lmiRS2 4 3 Dk2],D12,D21); %#1:D12*Dk*D21
lmiterm([lmiRS2 4 4 gam],-1,1); %#1:-gam
%-----
lmiPL12=newlmi;
lmiterm([lmiPL12 1 1 R],A2,1,'s'); %#2:R*A'+A*R
lmiterm([lmiPL12 1 1 Ck2],B2,1,'s'); %#2:Ck'*B2'+B2*Ck
lmiterm([lmiPL12 2 1 Ak2],1,1); %#2:Ak
lmiterm([lmiPL12 1 2 0],A2); %#2:A
lmiterm([lmiPL12 1 2 Dk2],B2,C2); %#2:B2*Dk*C2
lmiterm([lmiPL12 2 2 S],1,A2,'s'); %#2:A'*S+S*A
lmiterm([lmiPL12 2 2 Bk2],1,C2,'s'); %#2:C2'*Bk'+Bk*C2
%
lmiterm([lmiPL12 1 1 R],2*alpha,1); %#2:2*alpha*R
lmiterm([lmiPL12 2 1 0],2*alpha); %#2:2*alpha*I
lmiterm([lmiPL12 2 2 S],2*alpha,1); %#2:2*alpha*S
%-----
lmiPL22=newlmi;
lmiterm([lmiPL22 1 1 R],-r,1); %#3:-r*R
lmiterm([lmiPL22 2 1 0],-r); %#3:-r*I
lmiterm([lmiPL22 2 2 S],-r,1); %#3:-r*S
%
lmiterm([lmiPL22 1 3 R],A2,1); %#3:A*R
lmiterm([lmiPL22 1 3 Ck2],B2,1); %#3:B2*Ck
lmiterm([lmiPL22 2 3 Ak2],1,1); %#3:Ak
lmiterm([lmiPL22 1 4 0],A2); %#3:A
lmiterm([lmiPL22 1 4 Dk2],B2,C2); %#3:B2*Dk*C2
lmiterm([lmiPL22 2 4 S],1,A2); %#3:S*A
lmiterm([lmiPL22 2 4 Bk2],1,C2); %#3:Bk*C2
%
lmiterm([lmiPL22 3 3 R],-r,1); %#3:-r*R
lmiterm([lmiPL22 4 3 0],-r); %#3:-r*I
lmiterm([lmiPL22 4 4 S],-r,1); %#3:-r*S
%-----
sth=sin(th); cth=cos(th);
lmiPL32=newlmi;
lmiterm([lmiPL32 1 1 R],sth*A2,1,'s'); %#4:sth*(R*A'+A*R)
lmiterm([lmiPL32 1 1 Ck2],sth*B2,1,'s');%#4:sth*(Ck'*B2'+B2*Ck)
lmiterm([lmiPL32 2 1 Ak2],sth,1); %#4:sth*(Ak)
lmiterm([lmiPL32 1 2 0],sth*A2); %#4:sth*(A)
lmiterm([lmiPL32 1 2 Dk2],sth*B2,C2); %#4:sth*(B2*Dk*C2)
lmiterm([lmiPL32 2 2 S],1,sth*A2,'s'); %#4:sth*(A'*S+S*A)
lmiterm([lmiPL32 2 2 Bk2],1,sth*C2,'s');%#4:sth*(C2'*Bk'+Bk*C2)
%
lmiterm([lmiPL32 1 3 R],cth*A2,1); %#1:cth*(A*R)
lmiterm([lmiPL32 1 3 R],1,-cth*A2'); %#1:cth*(-R*A')
lmiterm([lmiPL32 1 3 Ck2],cth*B2,1); %#1:cth*(B*Ck)
lmiterm([lmiPL32 1 3 -Ck2],-cth*B2',1); %#1:cth*(-Ck'*B')
lmiterm([lmiPL32 2 3 Ak2],cth,1); %#4:cth*(Ak)
lmiterm([lmiPL32 1 4 -Ak2],-cth,1); %#4:cth*(-Ak')
lmiterm([lmiPL32 1 4 0],A2); %#4:cth*(A)
lmiterm([lmiPL32 2 3 0],-A2'); %#4:cth*(-A')
lmiterm([lmiPL32 1 4 Dk2],cth*B2,C2); %#4:cth*(B2*Dk*C2)
lmiterm([lmiPL32 2 3 -Dk2],-cth*C2',B2');%#4:cth*(-C2'*Dk'*B2')
lmiterm([lmiPL32 2 4 S],1,cth*A2); %#4:cth*(S*A)
lmiterm([lmiPL32 2 4 S],-cth*A2',1); %#4:cth*(-A'*S)
lmiterm([lmiPL32 2 4 Bk2],1,cth*C2); %#4:cth*(Bk*C2)
lmiterm([lmiPL32 2 4 -Bk2],-cth*C2',1); %#4:cth*(-C2'*Bk')
%
lmiterm([lmiPL32 3 3 R],sth*A2,1,'s'); %#4:sth*(R*A'+A*R)
lmiterm([lmiPL32 3 3 Ck2],sth*B2,1,'s');%#4:sth*(Ck'*B2'+B2*Ck)
lmiterm([lmiPL32 4 3 Ak2],sth,1); %#4:sth*(Ak)
lmiterm([lmiPL32 3 4 0],sth*A2); %#4:sth*(A)
lmiterm([lmiPL32 3 4 Dk2],sth*B2,C2); %#4:sth*(B2*Dk*C2)
lmiterm([lmiPL32 4 4 S],1,sth*A2,'s'); %#4:sth*(A'*S+S*A)
lmiterm([lmiPL32 4 4 Bk2],1,sth*C2,'s');%#4:sth*(C2'*Bk'+Bk*C2)
%=====
posX=-newlmi;
lmiterm([posX 1 1 R],1,1); %#5:R
lmiterm([posX 2 1 0],1); %#5:I
lmiterm([posX 2 2 S],1,1); %#5:S
%-----
lmiDk1=-newlmi;
lmiterm([lmiDk1 1 1 0],1e2); %#6:1e2
lmiterm([lmiDk1 2 2 0],1e2); %#6:1e2
lmiterm([lmiDk1 2 1 Dk1],1,1); %#6:Dk
%-----
lmiDk2=-newlmi;
lmiterm([lmiDk2 1 1 0],1e2); %#6:1e2
lmiterm([lmiDk2 2 2 0],1e2); %#6:1e2
lmiterm([lmiDk2 2 1 Dk2],1,1); %#6:Dk
%-----
lmig=newlmi;
lmiterm([lmig,1,1,gam],1,1); %#7:gam
lmiterm([lmig,1,1,0],-1e3); %#7:1e3
LMIs=getlmis;
end
%-----
%eof
|
![]()
![]()
![]() を乱数を100個発生させて所定の範囲内で変化させるとき、台車2に対してインパルス外乱が加わるときの
を乱数を100個発生させて所定の範囲内で変化させるとき、台車2に対してインパルス外乱が加わるときの![]() の振舞いのシミュレーションを行ってみます。
の振舞いのシミュレーションを行ってみます。
![]() の振舞い
の振舞い![]()
![]() とします。
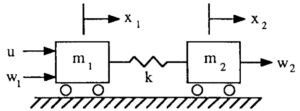
とします。![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc} m_1 & 0 \\ 0 & m_2 \end{array}\right] }_{M} \underbrace{ \left[\begin{array}{c} \ddot{x}_1(t)\\ \ddot{x}_2(t) \end{array}\right] }_{\ddot{x}(t)} +\underbrace{ \left[\begin{array}{cc} k & -k \\ -k & -k \end{array}\right] }_{K(k)} \underbrace{ \left[\begin{array}{ccc} {x}_1(t)\\ {x}_2(t) \end{array}\right] }_{{\xi}(t)} =\underbrace{ \left[\begin{array}{ccc} 1\\ 0 \end{array}\right] }_{E_{2\times1}}u(t) +\underbrace{ \left[\begin{array}{ccc} w_{1}\\ w_{2} \end{array}\right] }_{w_{d}} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c378c02aa9343c10a7c74dacb7a82030_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} \left[\begin{array}{c} \dot{\xi}(t)\\ \ddot{\xi}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cccc} 0_{2\times2} & I_2\\ -M^{-1}K & -M^{-1}D \end{array}\right] }_{A(k)} \left[\begin{array}{c} {\xi}(t)\\ \dot{\xi}(t) \end{array}\right]\\ + \left[\begin{array}{c} 0_{2\times1}\\ M^{-1}E_{2\times1} \end{array}\right]u(t) + \left[\begin{array}{c} 0_{2\times2}\\ M^{-1} \end{array}\right]w_d \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b16d7bf6b82863e883f1235ec5f0459f_l3.png)
![]() に対する次の内分式に注目します。
に対する次の内分式に注目します。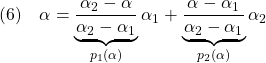
![]()
![]() のとき、上の状態方程式は、端点モデル
のとき、上の状態方程式は、端点モデル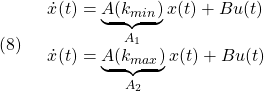
![]() によって重み付けして、LPVモデル
によって重み付けして、LPVモデル![]()
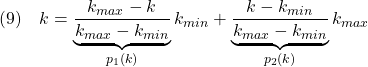

![Rendered by QuickLaTeX.com \displaystyle{(11) P: \left\{\begin{array}{l} \left[\begin{array}{c} \dot{\xi}\\ \ddot{\xi} \end{array}\right] = \underbrace{ \left[\begin{array}{cccc} 0_{2\times2} & I_2\\ -M^{-1}K & -M^{-1}D \end{array}\right] }_{A(k)=p_1(k)A_1+p_2(k)A_2} \left[\begin{array}{c} {\xi}\\ \dot{\xi} \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0_{2\times2}\\ M^{-1} \end{array}\right] }_{B_1} w_d + \underbrace{ \left[\begin{array}{c} 0_{2\times1}\\ M^{-1}E_{2\times1} \end{array}\right] }_{B_2} u\\ \underbrace{ \left[\begin{array}{c} x_2-x_1 \\ x_1\\ 2u \end{array}\right] }_{y_1} = \underbrace{ \left[\begin{array}{cc|cc} -1 & 1 & 0 & 0\\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ \end{array}\right] }_{C_1} \left[\begin{array}{c} {\xi}\\ \dot{\xi} \end{array}\right] + \underbrace{ 0_{3\times2} }_{D_{11}} w_d + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ 2 \end{array}\right] }_{D_{12}} u \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fd10d68cfea1b96cad0cc36a09499c1f_l3.png)
![]() を乱数を100個発生させて所定の範囲内で変化させるとき、台車2に対してインパルス外乱が加わるときの台車1の変位
を乱数を100個発生させて所定の範囲内で変化させるとき、台車2に対してインパルス外乱が加わるときの台車1の変位![]() と操作入力
と操作入力![]() の振舞いのシミュレーションを次に示します。
の振舞いのシミュレーションを次に示します。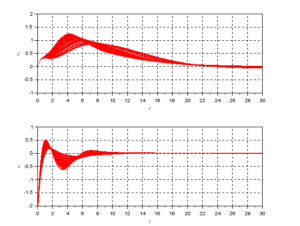
![Rendered by QuickLaTeX.com \displaystyle{(12) P: \left\{\begin{array}{l} \left[\begin{array}{c} \dot{\xi}\\ \ddot{\xi} \end{array}\right] = \underbrace{ \left[\begin{array}{cccc} 0_{2\times2} & I_2\\ -M^{-1}K & -M^{-1}D \end{array}\right] }_{A(k)=p_1(k)A_1+p_2(k)A_2} \left[\begin{array}{c} {\xi}\\ \dot{\xi} \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0_{2\times2}\\ M^{-1} \end{array}\right] }_{B_1} w_d + \underbrace{ \left[\begin{array}{c} 0_{2\times1}\\ M^{-1}E_{2\times1} \end{array}\right] }_{B_2} u\\ \underbrace{ \left[\begin{array}{c} x_2-x_1 \\ x_1\\ 2u \end{array}\right] }_{y_1} = \underbrace{ \left[\begin{array}{cc|cc} -1 & 1 & 0 & 0\\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ \end{array}\right] }_{C_1} \left[\begin{array}{c} {\xi}\\ \dot{\xi} \end{array}\right] + \underbrace{ 0_{3\times2} }_{D_{11}} w_d + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ 2 \end{array}\right] }_{D_{12}} u\\ \underbrace{ x_1 }_{y_2} = \underbrace{ \left[\begin{array}{cc|cc} 1 & 0 & 0 & 0 \end{array}\right] }_{C_2} \left[\begin{array}{c} {\xi}(t)\\ \dot{\xi}(t) \end{array}\right] + \underbrace{ 0_{1\times2} }_{D_{21}} w_d + \underbrace{ 0 }_{D_{22}} u \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b47f09bca2397aecd1d9f8e133a5ca01_l3.png)
![]() を乱数を100個発生させて所定の範囲内で変化させるとき、台車2に対してインパルス外乱が加わるときの台車1の変位
を乱数を100個発生させて所定の範囲内で変化させるとき、台車2に対してインパルス外乱が加わるときの台車1の変位![]() と操作入力
と操作入力![]() の振舞いのシミュレーションを次に示します。
の振舞いのシミュレーションを次に示します。
![]() 図2のグラフを描く、次のコードを説明せよ
図2のグラフを描く、次のコードを説明せよ![]() 図3のグラフを描く、次のコードを説明せよ。
図3のグラフを描く、次のコードを説明せよ。