円制約LMI | 制御系CAD

円制約LMI…Homework

[1] 次の領域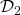 ${\cal D}_2$ を考えます。

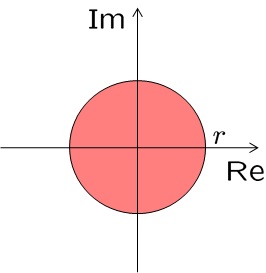
図1 領域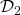 ${\cal D}_2$

このとき、次の命題が成り立ちます。

$\displaystyle{(8)\quad \begin{array}{lll} &&\lambda(A)\subset {\cal D}_2=\{s=x+jy\in{\rm\bf C}: \left[\begin{array}{cc} -r & s \\ s^* & -r \end{array}\right] <0 \}\nonumber\\ &\Leftrightarrow& \exists X>0:\ \left[\begin{array}{cc} -rX & XA \\ A^TX & -rX \end{array}\right]<0 \nonumber\\ &\Leftrightarrow& \exists Y>0:\ \left[\begin{array}{cc} -rY & AY \\ YA^T & -rY \end{array}\right]<0\nonumber \end{array} }$

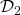●実際、まず領域 ${\cal D}_2$ が上図を表すことは、次のように確かめられます。

$\displaystyle{(9)\quad \begin{array}{lll} && \left[\begin{array}{cc} -r & s \\ s^* & -r \end{array}\right]<0\\ &\Leftrightarrow& (-r)-s\frac{1}{(-r)}s^*<0,\ -r<0 \nonumber\\ &\Leftrightarrow& r^2-(x+jy)(x-jy)>0 \nonumber\\ &\Leftrightarrow& x^2+y^2<r^2 \nonumber\end{array}}$

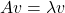●次に、十分性は、 $Av=\lambda v$ とすると、次のように確かめられます。

$\displaystyle{(10)\quad \begin{array}{lll} &&\left[\begin{array}{cc}v^{*T}&0^{T}\\0^{T}&v^{*T}\end{array}\right] \left[\begin{array}{cc}-rX&XA\\A^TX&-rX\end{array}\right] \left[\begin{array}{cc}v&0\\0&v\end{array}\right]\nonumber\\ &=& \left[\begin{array}{cc} -rv^{*T}Xv&v^{*T}X(\lambda v)\\ (\lambda^*v^{*T})Xv&-rv^{*T}Xv& \end{array}\right]\nonumber\\ &=& \underbrace{ \left[\begin{array}{cc} -r&\lambda\\\lambda^*&-r \end{array}\right] }_{<0} \underbrace{v^{*T}xv}_{>0}<0 \nonumber \end{array} }$

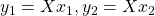さらに、 $y_1=Xx_1,y_2=Xx_2$ とおくと、次が成り立ちます。

$\displaystyle{(11)\quad \begin{array}{lll} && \left[\begin{array}{cc} x_1^T & x_2^T \end{array}\right] \left[\begin{array}{cc} -rX & XA \\ A^TX & -rX \end{array}\right] \left[\begin{array}{c} x_1\\ x_2 \end{array}\right] <0 \quad (\forall x_1,x_2\ne0)\nonumber\\ &\Leftrightarrow& \left[\begin{array}{cc} x_1^TX & x_2^TX \end{array}\right] \left[\begin{array}{cc} -rX^{-1} & AX^{-1} \\ X^{-1}A^T & -rX^{-1} \end{array}\right] \left[\begin{array}{c} Xx_1\\ Xx_2 \end{array}\right] <0 \nonumber\\ &\Leftrightarrow& \left[\begin{array}{cc} y_1^T & y_2^T \end{array}\right] \left[\begin{array}{cc} -rY & AY \\ YA^T & -rY \end{array}\right] \left[\begin{array}{c} y_1\\ y_2 \end{array}\right] <0 \quad (\forall y_1,y_2\ne0)\nonumber \end{array} }$

必要性については、あとで述べます。

演習B12…Flipped Classroom
$1^\circ$ 円制約を調べる次のコードを説明せよ。

MATLAB

%ana_lmi2.m
%-----
 A=[0 1;-2 -3]; n=2;
%-----
 setlmis([]);  
 X=lmivar(1,[n 1]);  
%-----
 q=0; r=1.5;
 lmi1=newlmi; 
 lmiterm([lmi1 1 1 X],-r,1);     %#1:   
 lmiterm([lmi1 1 2 X],1,A);      %#1:2*alpha*X  
 lmiterm([lmi1 2 2 X],-r,1);     %#1: 
%
 lmi2=newlmi;  
 lmiterm([-lmi2 1 1 X],1,1);     %#2:X  
%-----
 LMIs=getlmis;  
 [tmin,xfeas]=feasp(LMIs);  
 X=dec2mat(LMIs,xfeas,X)
%-----
%eof

$2^\circ$ 次の領域を表す ${\rm\bf LMI}$ を導出し、これをチェックするプログラムを作成せよ。

$\displaystyle{(17)\quad \lambda(A)\subset{\cal D}_4=\{s=x+jy\in{\rm\bf C}: \frac{x^2}{a^2}+\frac{y^2}{b^2}<1\} }$

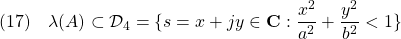
$\displaystyle{(18)\quad \begin{array}{lll} &&\frac{x^2}{a^2}+\frac{y^2}{b^2}<1\Leftrightarrow\frac{(\frac{s+s^*}{2})^2}{a^2}+\frac{(\frac{s-s^*}{2j})^2}{b^2}<1 \\ &&\Leftrightarrow\ b^2(s+s^*)^2-a^2(s-s^*)^2<4a^2b^2\\ &&\Leftrightarrow\ (b(s+s^*)+a(s-s^*))(b(s+s^*)-a(s-s^*))<4a^2b^2 \\ &&\Leftrightarrow\ -4a^2b^2+((b+a)s+(b-a)s^*))((b-a)s+(b+a)s^*))<0 \\ &&\Leftrightarrow\ \left[\begin{array}{cc} -4a^2b^2 & (b+a)s+(b-a)s^* \\ (b-a)s+(b+a)s^* & -1 \end{array}\right]<0 \end{array} }$

MATLAB

%ana_lmi2a.m
%-----
 A=[0 1;-1 -2]; n=2;
%-----
 setlmis([]);  
 X=lmivar(1,[n 1]);  
%-----
 a=2; b=1;
%  LMI1=-[-4*a^2*b^2*X (b+a)*X*A+(b-a)*A'*X;
%         (b-a)*X*A+(b+a)*A'*X -X];   
 lmi1=newlmi; 
 lmiterm([lmi1 1 1 X],-4*a^2*b^2,1);  %#1:-4*a^2*b^2*X  
 lmiterm([lmi1 1 2 X],b+a,A);         %#1:(b+a)*X*A
 lmiterm([lmi1 1 2 X],(b-a)*A',1);    %#1:(b-a)*A'*X
 lmiterm([lmi1 2 2 X],-1,1);          %#1:-X
%
 lmi2=newlmi;  
 lmiterm([-lmi2 1 1 X],1,1);     %#2:X  
%-----
 LMIs=getlmis;  
 [tmin,xfeas]=feasp(LMIs);  
 X=dec2mat(LMIs,xfeas,X)
%-----
%eof

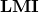$3^\circ$ 　次の領域を表す ${\rm\bf LMI}$ を導出し、これをチェックするプログラムを作成せよ。

$\displaystyle{(19)\quad \lambda(A)\subset{\cal D}_5=\{s=x+jy\in{\rm\bf C}: \frac{x^2}{a^2}-\frac{y^2}{b^2}>1, x<-a\} }$

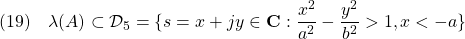
$\displaystyle{(20)\quad \begin{array}{lll} &&\frac{x^2}{a^2}-\frac{y^2}{b^2}>1,\ x<-a\ \Leftrightarrow\ \frac{(\frac{s+s^*}{2})^2}{a^2}-\frac{(\frac{s-s^*}{2j})^2}{b^2}>1,\ \frac{s+s^*}{2}<-a}\\ &&\Leftrightarrow\ b^2(s+s^*)^2+a^2(s-s^*)^2>4a^2b^2,\ s+s^*+2a<0\\ &&\Leftrightarrow\ b^2(s+s^*+2a)(s+s^*-2a)+a^2(s-s^*)^2>0,\ s+s^*+2a<0\\ &&\Leftrightarrow\ b(s+s^*-2a)-\frac{-a^2(s-s^*)^2}{b(s+s^*+2a)}<0,b(s+s^*+2a)<0\\ &&\Leftrightarrow\ \left[\begin{array}{cc} b(s+s^*+2a) & a(s-s^*) \\ -a(s-s^*) & b(s+s^*-2a) \end{array}\right]<0 \end{array} }$

MATLAB

%ana_lmi2b.m
%-----
 A=[0 1;-1 -2]; n=2;
%-----
 setlmis([]);  
 X=lmivar(1,[n 1]);  
%-----
 a=2; b=sqrt(2); f=sqrt(a^2+b^2);
%  LMI1=-[b*(X*A+A'*X+2a*X) a*(X*A-A'*X);
%        -a*(X*A-A'*X) b*(X*A+A'*X-2a*X)];
 lmi1=newlmi; 
 lmiterm([lmi1 1 1 X],b,A,'s');       %#1:b*(X*A+A'*X)
 lmiterm([lmi1 1 1 X],2*a*b,1);       %#1:2*a*b*X
 lmiterm([lmi1 1 2 X],a,A);           %#1:a*X*A
 lmiterm([lmi1 1 2 X],-a*A',1);       %#1:-a*A'*X
 lmiterm([lmi1 2 2 X],b,A,'s');       %#1:b*(X*A+A'*X)
 lmiterm([lmi1 2 2 X],-2*a*b,1);      %#1:-2*a*b*X
%
 lmi2=newlmi;  
 lmiterm([-lmi2 1 1 X],1,1);     %#2:X  
%-----
 LMIs=getlmis;  
 [tmin,xfeas]=feasp(LMIs);  
 X=dec2mat(LMIs,xfeas,X)
%-----
%eof