出力数=入力数の場合…Homework
これまでは、SM制御則の線形制御部を状態フィードバックの形で求めていましたが、以下では出力フィードバックに置き換えることを検討していきます。
[1] 制御対象の状態空間表現として次式を考えます。
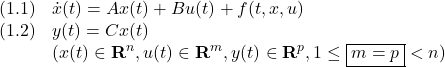
ただし、![]() はモデル誤差、非線形要素、外乱などの影響を表し、次のマッチング条件を満たすとします。
はモデル誤差、非線形要素、外乱などの影響を表し、次のマッチング条件を満たすとします。
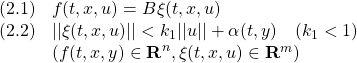
これに対し、次のスイッチング関数を定義します。
![]()
●状態方程式(1.1)は次のSM標準形をとるように座標変換されているとします(Note C22-1参照)。
![Rendered by QuickLaTeX.com \displaystyle{(4.1)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} \underbrace{(u(t)+\xi(t,x,u))}_{u'(t)}\\ (x_1(t)\in{\rm\bf R}^{n-m}, x_2(t)\in{\rm\bf R}^m, B_2\in{\rm\bf R}^{m\times m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9d9eabcd36c3ce62bf09a0d32ce9ea07_l3.png)
これに対応して、観測方程式(1.2)も次のように表しておきます。
![Rendered by QuickLaTeX.com \displaystyle{(4.2)\quad y(t)= \underbrace{ \left[\begin{array}{cc} C_{1} & C_{2} \\ \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)}\quad (y(t)\in{\rm\bf R}^m, C_2\in{\rm\bf R}^{m\times m}) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6b6bf798fce1fca1e7b12540a2a4e9a3_l3.png)
すなわち、以下では行列![]() は(4.1)と(4.2)のような分割をもつとします。
は(4.1)と(4.2)のような分割をもつとします。
●スイッチング関数(3)を
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad s(t)=Fy(t)=F \underbrace{ \left[\begin{array}{cc} C_{1} & C_{2} \\ \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} =\underbrace{ \left[\begin{array}{cc} FC_{1} & FC_{2} \\ \end{array}\right] }_{S=FC} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a3e37089e535379edc227db046808e5a_l3.png)
と表すと、等価制御が存在する前提条件![]() は
は
![]()
となります。以下では![]() を仮定します。このとき、正方行列
を仮定します。このとき、正方行列![]() はすべて正則となります。
はすべて正則となります。
[2] (4.1)に対して、座標変換
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{\bar{x}(t)} = \underbrace{ \left[\begin{array}{cc} I_{n-m}& 0 \\ C_1 & C_2 \\ \end{array}\right] }_{T_y} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} = \underbrace{ \left[\begin{array}{cc} I_{n-m}& 0 \\ -C_2^{-1}C_1 & C_2^{-1} \end{array}\right] }_{T_y^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{\bar{x}(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-36294dfd18793309878ccd0d8385bbb5_l3.png)
を行うために、まず(7)を(4.1)に代入して(![]() )
)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc} I_{n-m} & 0 \\ -M & C_2^{-1} \\ \end{array}\right] }_{T_y^{-1}} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot y(t) \end{array}\right] }_{\dot{\bar{x}}(t)}\\ = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{cc} I_{n-m} & 0 \\ -M & C_2^{-1} \\ \end{array}\right] }_{T_y^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{\bar{x}(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u'(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-09b99785d09eb2ea3c9cda05273c87f9_l3.png)
を得て、左から![]() をかけて
をかけて
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot y(t) \end{array}\right] }_{\dot{\bar{x}}(t)} = \underbrace{ \left[\begin{array}{cc} I_{n-m} & 0 \\ C_1 & C_2 \\ \end{array}\right] }_{T_y} \underbrace{ \left[\begin{array}{cc} A_{11}-A_{12}M & A_{12}C_2^{-1} \\ A_{21}-A_{22}M & A_{22}C_2^{-1} \\ \end{array}\right] }_{AT_y^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{\bar{x}(t)}\\ + \underbrace{ \left[\begin{array}{cc} I_{n-m} & 0 \\ C_1 & C_2 \\ \end{array}\right] }_{T_y} \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u'(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-576672e3c0ab015015806803be5be6e0_l3.png)
すなわち、次式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \boxed{ %\begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot y(t) \end{array}\right] }_{\dot{\bar{x}}(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ \bar{A}_{21} & \bar{A}_{22}\\ \end{array}\right] }_{\bar{A}=T_y A T_y^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{\bar{x}(t)} + \underbrace{ \left[\begin{array}{c} 0\\ \bar{B}_2 \end{array}\right] }_{\bar{B}=T_yB} u'(t) %\end{array} }}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-551b974cb60f73d29035528b00414fb6_l3.png)
ただし
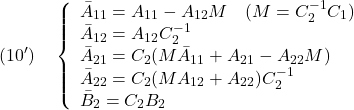
また、(4.2)と(3)は、次式のように表せます。
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \boxed{y(t)= \underbrace{ \left[\begin{array}{cc} 0 & I_{m} \\ \end{array}\right] }_{\bar{C}=CT_y^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{\bar{x}(t)}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6d572a784a0d5d01341f3c1a7bf72075_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \boxed{s(t)=Fy(t)= \underbrace{ \left[\begin{array}{cc} 0 & F \\ \end{array}\right] }_{F\bar{C}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{\bar{x}(t)}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5b3fac9c95c90b06d76da8172b3c27ba_l3.png)
ここで、![]() の固有値が
の固有値が ![]() の不変零点に等しく、スライディングモードの振舞いを決めます。しかし、
の不変零点に等しく、スライディングモードの振舞いを決めます。しかし、![]() ですから、
ですから、![]() には選択の自由度がないことに注意します。
には選択の自由度がないことに注意します。
[3] 以下では、(10),(11),(12)を考えますが、煩雑さを避けるために![]() 、
、![]() 、
、![]() 、
、![]() のバーをとって記述します。
のバーをとって記述します。
●さて、出力FB型のSM制御則として次式を考えます。
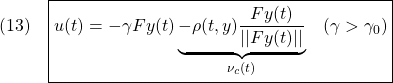
ここで、![]() と
と![]() は設計パラメータ、
は設計パラメータ、![]() は後で示す定数です。
は後で示す定数です。
これによる閉ループ系は、(13)を(4.1)に代入して、次式となります。
![]()
●このとき、SM制御則(13)を、2次安定性
![]()
が成り立つように決定します(![]() ,
, ![]() )。ただし、次式を仮定します。
)。ただし、次式を仮定します。
![]()
![]()
また、(17)と(13)から次式が得られることに注意します。
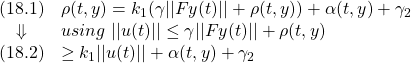
●これらの準備の下で、(15)が次のように示されます。
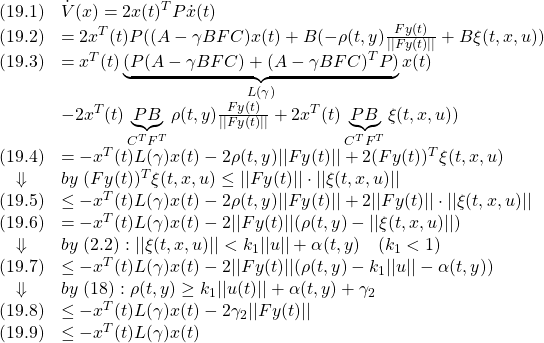
●ここで、次式を示すことができします。
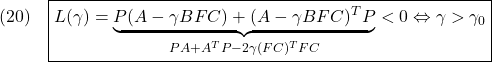
実際、左辺は
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{cl} (21.1) & L(\gamma)=PA+A^TP-2\gamma (FC)^TFC\\ (21.2) & =\underbrace{\left[ \begin{array}{cc} P_1 & 0 \\ 0 & P_2 \\ \end{array}\right]}_{P} \underbrace{\left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right]}_{A} + \underbrace{\left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right]^T}_{A^T} \underbrace{\left[\begin{array}{cc} P_1 & 0 \\ 0 & P_2 \\ \end{array}\right]}_{P}\\ &-2\gamma \underbrace{\left[\begin{array}{cc} 0 & F \\ \end{array}\right]^T}_{(FC)^T} \underbrace{\left[\begin{array}{cc} 0 & F \\ \end{array}\right]}_{FC}\\ (21.3) & =\left[ \begin{array}{cc} P_1A_{11}+A_{11}^TP_1 & P_1A_{12}+A_{21}^TP_2 \\ (P_1A_{12}+A_{21}^TP_2)^T & P_2A_{22}+A_{22}^TP_2 \\ \end{array}\right] -2\gamma \left[\begin{array}{cc} 0 & 0 \\ 0 & F^TF \\ \end{array}\right]\\ (21.4) & =\left[\begin{array}{cc} P_1A_{11}+A_{11}^TP_1 & P_1A_{12}+A_{21}^TP_2 \\ (P_1A_{12}+A_{21}^TP_2)^T & P_2A_{22}+A_{22}^TP_2-2\gamma F^TF \\ \end{array}\right]<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d90e2269d72fb880ea00c58c13b87908_l3.png)
となり、これは公式
![Rendered by QuickLaTeX.com \displaystyle{(22)\quad \begin{array}{l} \left[\begin{array}{cc} X & Z \\ Z^T & Y \end{array}\right]<0\\ \ \Leftrightarrow\ X-ZY^{-1}Z^T<0,\ Y<0 \\ \ \Leftrightarrow\ X<0,\ Y-Z^TX^{-1}Z<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5ad5723e74a49a0f86149626e8834da7_l3.png)
を用いて、以下と等価になります。
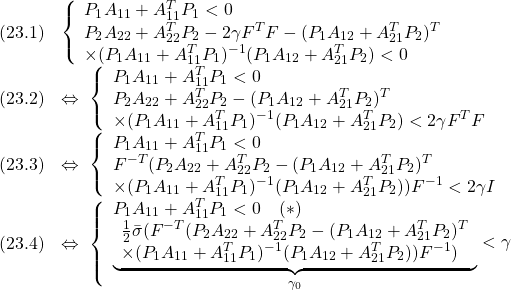
ここで、(*)は仮定より満足されるので、![]() が
が![]() となるための条件となることが分かります。
となるための条件となることが分かります。