特異値分解(Singular-Value Decomposition)
●![]() をサイズ
をサイズ![]() の行列(
の行列(![]() )とします。このとき、サイズ
)とします。このとき、サイズ![]() の直交行列
の直交行列![]() とサイズ
とサイズ![]() の直交行列
の直交行列![]() が存在して
が存在して
![]()
が成り立ちます。ここで、サイズ![]() の行列
の行列![]() は次を満たします。
は次を満たします。
![]()
![]()
●![]() だから、仮定
だから、仮定![]() より、
より、![]() は
は![]() 個の正固有値と
個の正固有値と![]() 個の零固有値をもち、互いに直交する固有ベクトルをもちます。そこで、
個の零固有値をもち、互いに直交する固有ベクトルをもちます。そこで、![]() の固有値の正の平方根を、大きい順に、
の固有値の正の平方根を、大きい順に、![]() のように表し、対応する固有ベクトル
のように表し、対応する固有ベクトル![]() を
を![]() を満足するようにとることができます。いま、
を満足するようにとることができます。いま、![]() を上のように、また
を上のように、また
![]()
とおくと、![]() は直交行列となり、つぎが成り立ちます。
は直交行列となり、つぎが成り立ちます。
![]()
第2式の左から、![]() をかけて
をかけて
![]()
また、![]() とおくと、第1式から
とおくと、第1式から![]() を得ます。そこで、
を得ます。そこで、![]() を
を![]() が直交行列となるように選ぶと
が直交行列となるように選ぶと
![]()
が成り立ちます。
●行列![]() の特異値分解は
の特異値分解は
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad A= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right] }_{U} \underbrace{ \left[\begin{array}{ccc} \sqrt{2} & 0 & 0 \\ 0 & 1 & 0 \end{array}\right] }_{\Sigma} \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0 \\ \frac{1}{\sqrt{2}} & 0 & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \end{array}\right]^T }_{V^T} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2af72a50a4707c3528e66ecddb5d79d3_l3.png)
のように与えられることを確かめます。
●![]() のサイズは
のサイズは![]() ですが、
ですが、![]() のサイズは
のサイズは![]() であるので、
であるので、![]() を計算すると
を計算すると![]() となります(サイズ
となります(サイズ![]() の行列
の行列![]() の特異値を手計算で求めるには、
の特異値を手計算で求めるには、![]() と
と![]() のが同じ非零固有値をもつことから、サイズの小さいほうの固有値計算を行えばよい)。これから、
のが同じ非零固有値をもつことから、サイズの小さいほうの固有値計算を行えばよい)。これから、![]() の固有値は
の固有値は![]() で、その正の平方根
で、その正の平方根![]() が特異値で、上の
が特異値で、上の![]() の対角成分の特異値は大きい順に並べる約束ですから
の対角成分の特異値は大きい順に並べる約束ですから
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \underbrace{ \left[\begin{array}{cc} 1 & 0 \\ 0 & 2 \end{array}\right] }_{AA^T} \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right] }_{U} = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right] }_{U} \underbrace{ \left[\begin{array}{cc} 2 & 0 \\ 0 & 1 \end{array}\right] }_{\Sigma_1^2} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6f51f7ede73c92e99db76c7c0af734a4_l3.png)
のように、![]() と
と![]() が決まります。つぎに、
が決まります。つぎに、![]() については、視察によって
については、視察によって
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \underbrace{ \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 1 & 1 \end{array}\right] }_{A^TA} \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0 \\ x & 0 & -y \\ y & 0 & x \end{array}\right] }_{V} = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0 \\ x & 0 & -y \\ y & 0 & x \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{ccc} 2 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{array}\right] }_{{\rm diag}\{\Sigma_1^2,0\}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-80803b0ba51318c2e2c0a244cacf7e45_l3.png)
とします。ここで、![]() と
と![]() が直交しており、
が直交しており、![]() の制約があります。上式から
の制約があります。上式から![]() が出て、
が出て、![]() と定まります。
と定まります。
行列のノルム
● ![]() から
から![]() への写像
への写像![]() の「伝達特性」をどう測るかを考えます。これはスカラの場合は正比例の関係
の「伝達特性」をどう測るかを考えます。これはスカラの場合は正比例の関係![]() ですから、比例定数
ですから、比例定数![]() に相当する量を求める話になります。
に相当する量を求める話になります。
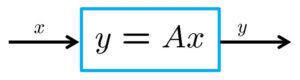
サイズ![]() の行列
の行列![]() の次の特異値分解を考えます。
の次の特異値分解を考えます。
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} A= \underbrace{ \left[\begin{array}{cc} U_1 & U_2 \end{array}\right] }_{U(m\times m)} \underbrace{ \left[\begin{array}{cc} {\rm diag}\{\sigma_1,\cdots,\sigma_k\} & 0_{k\times (n-k)} \\ 0_{(m-k)\times k} & 0_{(m-k)\times (n-k)} \end{array}\right] }_{\Sigma= \left[\begin{array}{cc} \Sigma_1 & 0 \\ 0 & 0 \end{array}\right] \quad(\sigma_1\ge\cdots\ge\sigma_k) } \underbrace{ \left[\begin{array}{cc} V_1^T \\ V_2^T \end{array}\right] }_{V(n\times n)^T}\\ =U_1(m\times k)\Sigma_1(k\times k)V_1(n\times k)^T \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dc89eab35a6815c659415bf9a11570b9_l3.png)
ここで、![]() で、
で、![]() と
と![]() は直交行列です。
は直交行列です。
![]()
したがって、次のような3つの線形写像に分解されます。
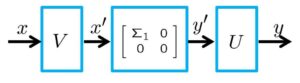
●![]() 次元ベクトル
次元ベクトル![]() のノルムとして、次の3通りが知られています。
のノルムとして、次の3通りが知られています。
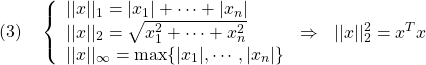
以下では、ベクトルのノルムとして、2番目の2ノルムを考えます。
このとき、次が成り立ちます。
![]()
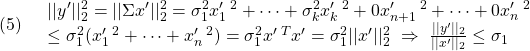
![]()
すなわち
![]()
したがって、線形写像![]() の伝達特性は、行列
の伝達特性は、行列![]() の2ノルム
の2ノルム
![]()
すなわち行列![]() の最大特異値
の最大特異値![]() (行列
(行列![]() または
または![]() の最大固有値の正の平方根)によって表されます。
の最大固有値の正の平方根)によって表されます。
●行列のノルムについて次式が成り立ちます。
![]()
(8)より
![]()
に注意して
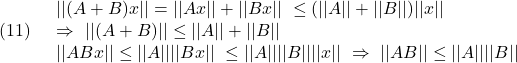
●一方、ベクトルの2ノルムについて次式が成り立ちます。
![]()
これらは(9)の特別な場合と考えられますが、ここでは直接導出してみます。
いま、![]() に関する2次方程式
に関する2次方程式
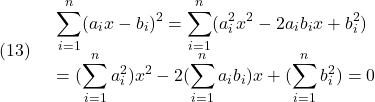
を考えると、この実数解は1個または0個となることから、この判別式は零または負でなければならないので

より
![]()
すなわち(12)の第2式が得られます。また、第1式は、次式から得られます。
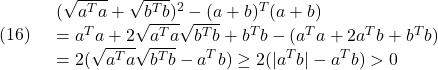
●ちなみに、行列のフロベニウスノルムは

で定義されます。これは
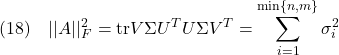
と表せるので、次式が成り立ちます。
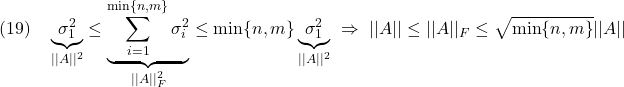
行列積のフロベニウスノルムについても

が成り立ちます。
連立1次方程式
次の線形方程式(連立1次方程式)を考えます。
![]()
ここで、![]() はフルランク(
はフルランク(![]() )とします。
)とします。
![]()
![]() の場合(未知数の数が方程式の数より大きい場合)、(1)はunder-determined(劣決定)と呼ばれ、
の場合(未知数の数が方程式の数より大きい場合)、(1)はunder-determined(劣決定)と呼ばれ、![]() の特異値分解を代入して次のように書けます。
の特異値分解を代入して次のように書けます。
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \begin{array}{l} \underbrace{U\left[\begin{array}{cc} \Sigma_1 & 0_{n\times m-n} \end{array}\right] \left[\begin{array}{c} V_1^H\\ V_2^H \end{array}\right]}_{A}x =U\Sigma_1V_1^Hx=b\\ \Sigma_1={\rm diag}\{\sigma_1,\cdots,\sigma_n\} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2633ba4a0b1a6e8db6ae07669f36a2f2_l3.png)
(2)の解候補として
![]()
を考えます。![]() より第1項と第2項は直交することから
より第1項と第2項は直交することから
![]()
(3)において![]() として得られる
として得られる![]() は、
は、![]() を最小化する最小ノルム解と呼ばれます。
を最小化する最小ノルム解と呼ばれます。
![]()
![]() の場合(未知数の数が方程式の数より小さい場合)、(1)はover-determined(過決定)と呼ばれ、
の場合(未知数の数が方程式の数より小さい場合)、(1)はover-determined(過決定)と呼ばれ、![]() の特異値分解を代入して次のように書けます。
の特異値分解を代入して次のように書けます。
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} \underbrace{\left[\begin{array}{cc} U_1 & U_2 \end{array}\right] \left[\begin{array}{cc} \Sigma_1 \\ 0_{n-m\times m} \end{array}\right]V^H}_{A}x =U_1\Sigma_1V^Hx=b\\ \Sigma_1={\rm diag}\{\sigma_1,\cdots,\sigma_m\} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-89dad140495fae168ea6b37fa797cbe0_l3.png)
(5)の解候補として
![]()
を考えます。![]() において、
において、
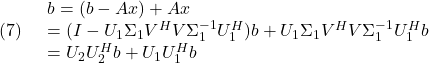
ここで、![]() より第1項と第2項は直交することから
より第1項と第2項は直交することから
![]()
(6)は![]() を最小化する最小2乗解と呼ばれます。
を最小化する最小2乗解と呼ばれます。