2慣性系の制御について、次の論文をフォローします。
2慣性系…Homework
[0] 次図のような2慣性系を考えます。
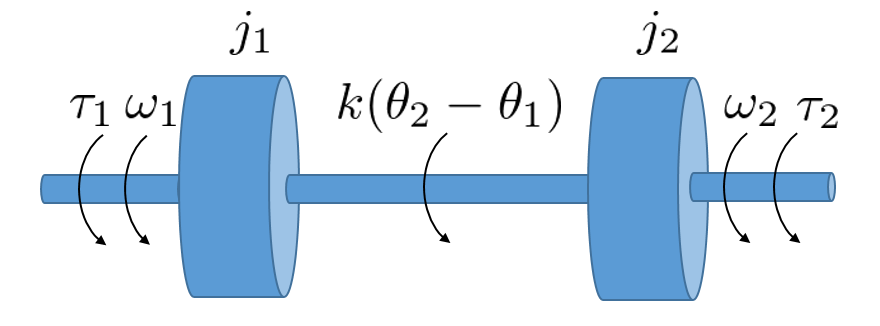
これは次の運動方程式で表されます。
![]()
ここで、![]() を操作トルク、
を操作トルク、![]() を外乱トルクとみなし、また
を外乱トルクとみなし、また
![]()
は軸トルクと呼ばれ、計測可能とします。これを用いると(1)は次式となります。
![]()
以下では、一定の角速度での回転時に、大きさ1の定値外乱トルクが発生しても、望ましい角速度![]() での回転させる速度制御問題を検討します。回転体1の速度制御ですから基本はPI制御ですが、回転体2からの外乱トルクの影響を除くために、軸トルク(両軸のトルク差)のFBも考慮します(回転体2の角速度はFBしません)。両回転体の慣性モーメントの大小によって制御ゲインは変わることになります。
での回転させる速度制御問題を検討します。回転体1の速度制御ですから基本はPI制御ですが、回転体2からの外乱トルクの影響を除くために、軸トルク(両軸のトルク差)のFBも考慮します(回転体2の角速度はFBしません)。両回転体の慣性モーメントの大小によって制御ゲインは変わることになります。
[1] 軸トルクFBを加えたPI制御
![]()
に注意して、次の状態方程式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \boxed{ \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{\tau}_s(t)\\ \dot{\omega}_1(t)\\ \dot{\omega}_2(t) \end{array}\right] }_{\dot{\xi}(t)} = \underbrace{ \left[\begin{array}{cccc} 0 & k & -k\\ -1/j_1 & 0 & 0\\ 1/j_2 & 0 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \tau_s(t)\\ \omega_1(t)\\ \omega_2(t) \end{array}\right] }_{\xi(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ 1/j_1 \\ 0 \end{array}\right] }_{B} \tau_1(t) + \underbrace{ \left[\begin{array}{c} 0\\ 0\\ 1/j_2 \end{array}\right] }_{w} \\ \omega_1(t)= \underbrace{ \left[\begin{array}{cccc} 0 & 1 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} \tau_s(t)\\ \omega_1(t)\\ \omega_2(t) \end{array}\right] }_{\xi(t)}\\ \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c25f6b237c7c2e6cd097ce7e72e81495_l3.png)
ここで、![]() から
から![]() までの伝達関数
までの伝達関数
![]()
から、次の共振角周波数![]() と反共振角周波数
と反共振角周波数![]() を定義しておきます。
を定義しておきます。
![]()
さて、制御目的が達成されているとすると
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \left[\begin{array}{c} 0\\ 0\\ -1/j_2\\ \omega^* \end{array}\right] = \underbrace{ \left[\begin{array}{cccc} 0 & k & -k & 0\\ -1/j_1 & 0 & 0 & 1/j_1\\ 1/j_2 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \end{array}\right] }_{S= \left[\begin{array}{cc} A & B\\ C & 0 \end{array}\right] } \left[\begin{array}{c} \tau_s(\infty)\\ \omega_1(\infty)\\ \omega_2(\infty)\\ \tau_1(\infty) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-200a8504b885306bfa297096ead9dcfa_l3.png)
より
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \underbrace{ \left[\begin{array}{c} \tau_s(\infty)\\ \omega_1(\infty)\\ \omega_2(\infty)\\ \tau_1(\infty) \end{array}\right] }_{\left[\begin{array}{c} \xi_\infty \\ \tau_{1,\infty} \end{array}\right]} = \underbrace{ \left[\begin{array}{cccc} 0 & 0 & j_2 & 0\\ 0 & 0 & 0 & 1\\ -1/k & 0 & 0 & 1\\ 0 & j_1 & j_2 &0\end{array}\right] }_{S^{-1}} \left[\begin{array}{c} 0\\ 0\\ -1/j_2\\ \omega^* \end{array}\right] = \left[\begin{array}{c} -1\\ \omega^*\\ \omega^*\\ -1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f0d4e810a55a6a882407932aaab00e86_l3.png)
を得ます。したがって
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \left[\begin{array}{c} \dot{\xi}(t) \\ \omega_1(t)-\omega^* \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ \tau_1(t)-\tau_{1,\infty} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-47d30f4e17805a9a2ebaefe39021995e_l3.png)
に注意して、偏差系
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \frac{d}{dt} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ \tau_1(t)-\tau_{1,\infty} \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ \tau_1(t)-\tau_{1,\infty} \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B_{E3}} \dot{\tau}_1(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a0ff98500da4e2f52af6872960bbcfc1_l3.png)
に対する安定化状態フィードバック
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \begin{array}{l} \dot{\tau}_1(t) = K_{E3} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ \tau_1(t)-\tau_{1,\infty} \end{array}\right] = \underbrace{ K_{E3}S^{-1} }_{ \left[\begin{array}{cccc} F_1 & F_2 & F_3 & F_4 \end{array}\right]} \left[\begin{array}{c} \dot{\xi}(t) \\ \omega_1(t)-\omega^* \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-20938eef1ea9c03b40aa65e259fc059d_l3.png)
すなわち
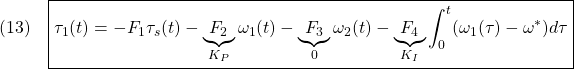
を求めます。
ここで本来は2次形式評価関数を設定したいところですが、ゲインに制約をつけるために、上記論文では閉ループ系の望ましい特性多項式を
![]()
と設定し、極配置問題を解いています。これは、たとえば
![]()
とすると
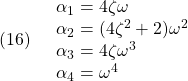
の形式になること、また減衰係数![]() と固有角周波数
と固有角周波数![]() を指定できるなどの理由によると思われます。
を指定できるなどの理由によると思われます。
上の望ましい特性多項式を達成する状態フィードバックゲインは、次式によって計算できます。
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad \begin{array}{l} K_{E3}= \left[\begin{array}{cccc} 0 & 0 & 0 & 1 \end{array}\right]\\ \times \left[\begin{array}{cccc} B_{E3} & A_{E3}B_{E3} & A_{E3}^2B_{E3} & A_{E3}^3B_{E3} \end{array}\right]^{-1}\\ \times (A_{E3}^4+\alpha_1 A_{E3}^3+\alpha_2 A_{E3}^2+\alpha_3 A_{E3}+\alpha_4 I_4) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-753bbdf4eade430b3af666ccdd104bc1_l3.png)
数式処理プログラムを用いて、
![]()
を代入して、次のように計算できます(![]() は論文中の記号)。
は論文中の記号)。
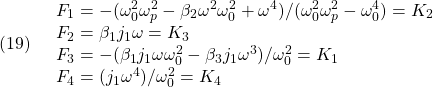
実際
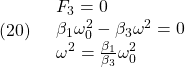
![]()
![]()
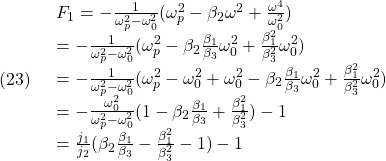
まず、負荷の角速度をFBしなくて済むためには、(20)が必要となり、![]() 自身には選択の余地はありません。興味深いのは、(23)から、軸トルクのFBゲインの符号が正にも負にもなることです。
自身には選択の余地はありません。興味深いのは、(23)から、軸トルクのFBゲインの符号が正にも負にもなることです。
| MAXIMA |
|
| MATLAB |
|
●数値微分による軸トルクを加えたPI制御
軸トルクは次式のように速度を1階微分して得ることができます。
![]()
これを用いると
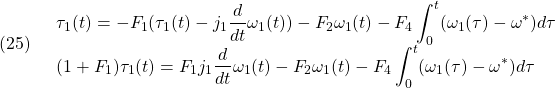
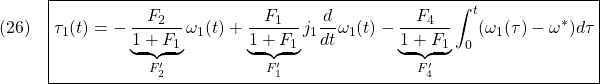
これはPID制御となっており、軸トルクのFBは不要となっています。
●外乱オブザーバによる軸トルクを加えたPI制御
外乱オブザーバの仕組みは、数値微分を用いた軸トルクを1次フィルタを通したものに等しいことが知られています。これは
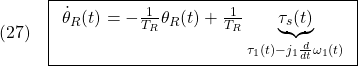
を用いて
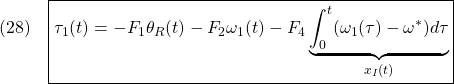
のように実施されます。以下では、これもPID制御であることを示します。
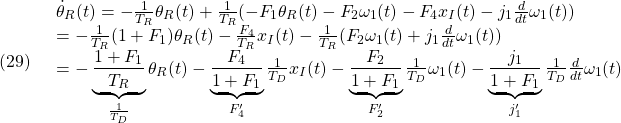
のように書けるので、コントローラの状態空間表現は次式となります(簡単のため![]() としています)。
としています)。
![Rendered by QuickLaTeX.com \displaystyle{(30)\quad \begin{array}{l} \left[\begin{array}{c} \dot{x}_I(t)\\ \dot{\theta}_R(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cccc} 0 & 0\\ -\frac{F'_4}{T_D} & -\frac{1}{T_D} \end{array}\right] }_{A_F} \left[\begin{array}{c} x_I(t)\\ \theta_R(t) \end{array}\right] + \underbrace{ \left[\begin{array}{cc} 1\\ -\frac{1}{T_D}(F'_2+j'_1\frac{d}{dt}) \end{array}\right] }_{B_F}\omega_1(t)\\ \tau_1(t)= \underbrace{ \left[\begin{array}{cccc} -F_4 & -F_1 \end{array}\right] }_{C_F} \left[\begin{array}{c} x_I(t)\\ \theta_R(t) \end{array}\right] +\underbrace{(-F_2)}_{D_F}\omega_1(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7e6311a39c4f39d2f6000e395385fed2_l3.png)
これからコントローラの伝達関数が次式のように計算できます。
![Rendered by QuickLaTeX.com \displaystyle{(31)\quad \begin{array}{l} K(s)=\underbrace{ \left[\begin{array}{cccc} -F_4 & -F_1 \end{array}\right] }_{C_F} \underbrace{ \left[\begin{array}{cccc} s & 0\\ \frac{F'_4}{T_D} & s+\frac{1}{T_D} \end{array}\right]^{-1} }_{(sI-A_F)^{-1}} \underbrace{ \left[\begin{array}{cc} 1\\ -\frac{1}{T_D}(F'_2+j'_1s) \end{array}\right] }_{B_F} + \underbrace{(-F_2)}_{D_F}\\ = \left[\begin{array}{cccc} -F_4 & -F_1 \end{array}\right] \underbrace{ \left[\begin{array}{cccc} s & 0\\ \frac{F'_4}{T_D} & s+\frac{1}{T_D} \end{array}\right]^{-1} }_{ \frac{1}{s(s+\frac{1}{T_D})} \left[\begin{array}{cccc} s+\frac{1}{T_D} & 0\\ -\frac{F'_4}{T_D} & s \end{array}\right] } \left[\begin{array}{cc} 1\\ -\frac{1}{T_D}(F'_2+j'_1s) \end{array}\right] -F_2\\ =-F_4\frac{1}{s}+F_1 \frac{F'_4}{T_D}\frac{1}{s(s+\frac{1}{T_D})} +F_1 \frac{1}{s+\frac{1}{T_D}}\frac{1}{T_D}(F'_2+j'_1s)-F_2\\ =-(1+F_1 )(F'_2+F'_4\frac{1}{s})+F_1 \frac{1}{T_Ds+1}(F'_4\frac{1}{s}+F'_2+j'_1s)\\ =(-1-F_1 +F_1 \frac{1}{T_Ds+1}})(F'_2+F'_4\frac{1}{s})+F_1'\frac{j_1s}{T_Ds+1}}\\ =(-1-F_1 \frac{T_Ds}{T_Ds+1}})(F'_2+F'_4\frac{1}{s})+F_1'\frac{j_1s}{T_Ds+1}}\\ =(-1-F'_1\frac{T_Rs}{T_Ds+1}})(F'_2+F'_4\frac{1}{s})+F_1'\frac{j_1s}{T_Ds+1}}\\ =-F'_2-F'_4\frac{1}{s}-\frac{T_Rs}{T_Ds+1}}F'_1F'_2-\frac{T_Ds+1-T_Ds}{T_Ds+1}}T_RF'_1F'_4+F_1'\frac{j_1s}{T_Ds+1}}\\ =-F'_2-T_RF'_1F'_2-F'_4\frac{1}{s}-\frac{T_Rs}{T_Ds+1}}F'_1F'_2+\frac{T_Ds}{T_Ds+1}}T_RF'_1F'_4+F_1'\frac{j_1s}{T_Ds+1}}\\ =-\underbrace{(F'_2+T_RF'_1F'_2)}_{K_P}-\underbrace{F'_4}_{K_I}\frac{1}{s}-\frac{s}{T_Ds+1}}\underbrace{(T_RF'_1F'_2-T_DT_RF'_1F'_4-F_1'j_1)}}_{K_D}\\ %=F_P+F_I\frac{1}{s}+\frac{F_Ds}{Ts+1} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4e1fa43bfe67aa01b18fdbf7cf206bd5_l3.png)
外乱オブザーバによる軸トルクを加えたPI制御は、1次フィルタ付微分動作をもつPID制御となっていることが分かります。
[2] 1次フィルタを通すPI制御
![]()
![Rendered by QuickLaTeX.com \displaystyle{(33)\quad \boxed{ \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{\tau}_s(t)\\ \dot{\omega}_1(t)\\ \dot{\omega}_2(t)\\ \dot{\tau}_1(t) \end{array}\right] }_{\dot{\xi}(t)} = \underbrace{ \left[\begin{array}{cccc} 0 & k & -k & 0\\ -1/j_1 & 0 & 0& 1/j_1\\ 1/j_2 & 0 & 0& 0\\ 0 & 0 & 0 & -1/T \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \tau_s(t)\\ \omega_1(t)\\ \omega_2(t)\\ \tau_1(t) \end{array}\right] }_{\xi(t)}\\ + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ 0 \\ 1/T \end{array}\right] }_{B} u(t) + \underbrace{ \left[\begin{array}{c} 0\\ 0\\ 1/j_2\\ 0 \end{array}\right] }_{w}\\ \dot{\theta}_1(t)= \underbrace{ \left[\begin{array}{cccc} 0 & 1 & 0& 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} \tau_s(t)\\ \omega_1(t)\\ \omega_2(t)\\ \tau_1(t) \end{array}\right] }_{\xi(t)}\\ \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0face941bc9b742fd8c1a39a6ab8905e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(34)\quad \left[\begin{array}{c} 0\\ 0\\ -1/j_2\\ 0\\ \omega^* \end{array}\right] = \underbrace{ \left[\begin{array}{ccccc} 0 & k & -k & 0& 0\\ -1/j_1 & 0 & 0 & 1/j_1& 0\\ 1/j_2 & 0 & 0 & 0& 0\\ 0 & 0 & 0 & -1/T& 1/T\\ 0 & 1 & 0 & 0& 0 \end{array}\right] }_{S} \left[\begin{array}{c} \tau_s(\infty)\\ \omega_1(\infty)\\ \omega_2(\infty)\\ \tau_1(\infty)\\ u(\infty) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3bb52aeb5920c21402cde26565f91792_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(35)\quad \underbrace{ \left[\begin{array}{c} \tau_s(\infty)\\ \omega_1(\infty)\\ \omega_2(\infty)\\ \tau_1(\infty)\\ u(\infty) \end{array}\right] }_{\left[\begin{array}{c} \xi_\infty \\ u_\infty \end{array}\right]} = \underbrace{ \left[\begin{array}{ccccc} 0 & 0 & j_2 & 0& 0\\ 0 & 0 & 0 & 0& 1\\ -1 & 0 & 0 & 0& 1\\ 0 & j_1 & j_2 &0& 0\\ 0 & j_1 & j_2 &T& 0 \end{array}\right] }_{S^{-1}} \left[\begin{array}{c} 0\\ 0\\ -1/j_2\\ 0\\ \omega^* \end{array}\right] = \left[\begin{array}{c} -1\\ \omega^*\\ \omega^*\\ -1\\ -1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-384becd060fafe8dca8773e3c0ab725e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(36)\quad \left[\begin{array}{c} \dot{\xi}(t) \\ \omega_1(t)-\omega^* \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ u(t)-u_\infty \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-428e35cc70942d6dbf93edd87c4e25db_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(37)\quad \frac{d}{dt} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ u(t)-u_\infty \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ u(t)-u_\infty \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B_{E3}} \dot{u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-06337a8f4ce7e3b2bf148980a4060511_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(38)\quad \dot{u}(t) = K_{E3} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ u(t)-u_\infty \end{array}\right] =\underbrace{ K_{E3}S^{-1} }_{ \left[\begin{array}{ccccc} K_2 & K_3 & K_1 & K_0& K_4 \end{array}\right]} \left[\begin{array}{c} \dot{\xi}(t) \\ \omega_1(t)-\omega^* \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c3735afe885bab43cef461836c34db22_l3.png)
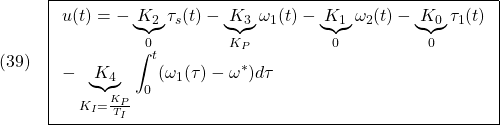
![]()
![]()
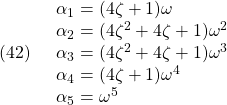
![Rendered by QuickLaTeX.com \displaystyle{(43)\quad \begin{array}{l} K_{E3}= \left[\begin{array}{ccccc} 0 & 0 & 0 & 0 &1 \end{array}\right]\\ \times \left[\begin{array}{ccccc} B_{E3} & A_{E3}B_{E3} & A_{E3}^2B_{E3} & A_{E3}^3B_{E3}& A_{E3}^4B_{E3} \end{array}\right]^{-1}\\ \times (A_{E3}^5+\alpha_1A_{E3}^4+\alpha_2A_{E3}^3+\alpha_3A_{E3}^2+\alpha_4A_{E3}+\alpha_5I_n) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c88f5d511bc275540dd02784c3de1ec1_l3.png)
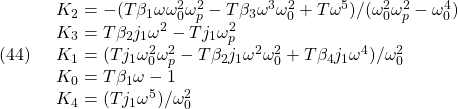
![]()
![]()
![]()
![]()
![]()
![]()
![]()
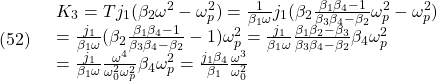
![]()
![]()
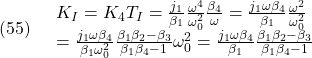
| MAXIMA |
|
| MATLAB |
|
[3] 1次フィルタ付微分動作をもつPID制御
![]()
![Rendered by QuickLaTeX.com \displaystyle{(57)\quad \boxed{ \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{\tau}_s(t)\\ \dot{\omega}_1(t)\\ \dot{\omega}_2(t)\\ \dot{x}_{D}(t)\\ \end{array}\right] }_{\dot{\xi}(t)} = \underbrace{ \left[\begin{array}{cccc} 0 & k & -k & 0\\ -1/j_1 & 0 & 0& 0\\ 1/j_2 & 0 & 0& 0\\ 0 & 1/T_D & 0 & -1/T_D \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \tau_s(t)\\ \omega_1(t)\\ \omega_2(t)\\ x_{D}(t)\\ \end{array}\right] }_{\xi(t)}\\ + \underbrace{ \left[\begin{array}{c} 0 \\ 1/j_1 \\ 0 \\ 0 \end{array}\right] }_{B} \tau_1(t) + \underbrace{ \left[\begin{array}{c} 0\\ 0\\ 1/j_2\\ 0 \end{array}\right] }_{w}\\ \omega_1(t)= \underbrace{ \left[\begin{array}{cccc} 0 & 1 & 0& 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} \tau_s(t)\\ \omega_1(t)\\ \omega_2(t)\\ x_{D}(t)\\ \end{array}\right] }_{\xi(t)}\\ \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-43c48213c969f1206fa859c02ec68ff6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(58)\quad \left[\begin{array}{c} 0\\ 0\\ -1/j_2\\ 0\\ \omega^* \end{array}\right] = \underbrace{ \left[\begin{array}{ccccc} 0 & k & -k & 0& 0\\ -1/j_1 & 0 & 0& 0& 1/j_1 \\ 1/j_2 & 0 & 0& 0& 0\\ 0 & 1/T_D & 0 & -1/T_D& 0\\ 0 & 1 & 0 & 0& 0 \end{array}\right] }_{S} \left[\begin{array}{c} \tau_s(\infty)\\ \omega_1(\infty)\\ \omega_2(\infty)\\ x_{D}(\infty)\\ \tau_1(\infty) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-32cb895bdb660d3f9a735af3dc6e1f03_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(59)\quad \underbrace{ \left[\begin{array}{c} \tau_s(\infty)\\ \omega_1(\infty)\\ \omega_2(\infty)\\ x_{D}(\infty)\\ \tau_1(\infty) \end{array}\right] }_{\left[\begin{array}{c} \xi_\infty \\ \tau_\infty \end{array}\right]} = \underbrace{ \left[\begin{array}{ccccc} 0 & 0 & j_2 & 0& 0\\ 0 & 0 & 0 & 0& 1\\ -1/k & 0 & 0 & 0& 1\\ 0 & 0 & 0 &-1/T_D& 0\\ 0 & j_1 & j_2 &0& 0 \end{array}\right] }_{S^{-1}} \left[\begin{array}{c} 0\\ 0\\ -1/j_2\\ 0\\ \omega^* \end{array}\right] = \left[\begin{array}{c} -1\\ \omega^*\\ \omega^*\\ \omega^*\\ -1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-42e9671105c1457bff74113d4e882b97_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(60)\quad \left[\begin{array}{c} \dot{\xi}(t) \\ \omega_1(t)-\omega^* \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ \tau_1(t)-\tau_\infty \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-451065a42216db1d57dd41f1a3b608e4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(61)\quad \frac{d}{dt} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ \tau_1(t)-\tau_\infty \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ \tau_1(t)-\tau_\infty \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B_{E3}} \dot{u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f08c8362eba9a30ffbce176f269d3428_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(62)\quad \begin{array}{l} \dot{\tau}_1(t)(t) = K_{E3} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ \tau_1(t)-\tau_\infty \end{array}\right]\\ =\underbrace{ K_{E3}S^{-1} }_{ \left[\begin{array}{ccccc} F_1(K_2) & F_2(K_3) & F_3(K_1) & F_4(K_0)& F_5(K_4) \end{array}\right]} \left[\begin{array}{c} \dot{\xi}(t) \\ \omega_1(t)-\omega^* \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-12a082ac3aaa6fa25b693f8371e7cdad_l3.png)
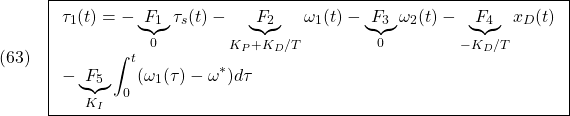
![]()
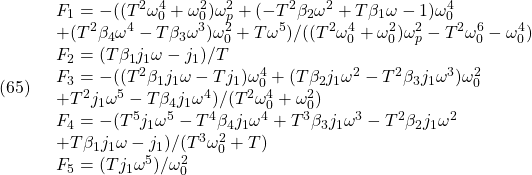
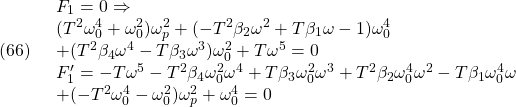
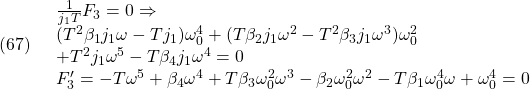
![]()
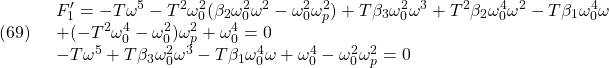
![]()
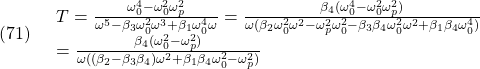
![]()
![]()
![]()
![]()
![]()
![]()
![]()
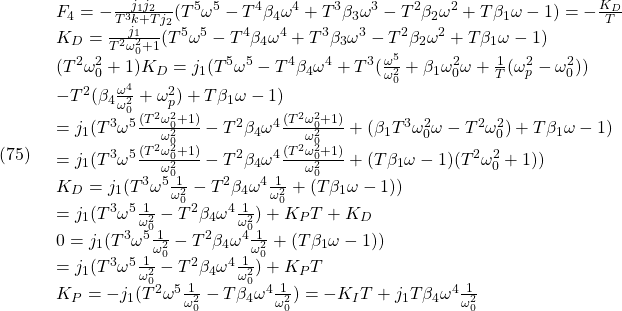
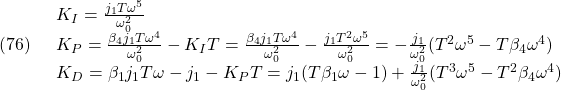
| MAXIMA |
|
| MATLAB |
|