LQ制御…Homework
[1] 可制御な制御対象
![]()
を安定化する状態フィードバック
![]()
の決定法を考えます。一つの方法は,閉ループ系
![]()
の時間応答に関する評価規範として,2次形式評価関数
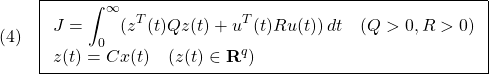
を設定し,これを最小化する問題を解くことです。ただし、![]() は可観測対とします。これによる状態フィードバックのゲイン行列
は可観測対とします。これによる状態フィードバックのゲイン行列![]() は,リッカチ方程式
は,リッカチ方程式
![]()
の解![]() を用いて,次式で与えられます。
を用いて,次式で与えられます。
![]()
この証明はNoteに示しています。
[2] 以下では、代表的な2次系に対して、評価関数を設定して、ゲイン行列![]() を求めてみます。その際、リッカチ方程式は4つの解候補を持ちますが、
を求めてみます。その際、リッカチ方程式は4つの解候補を持ちますが、![]() の条件、すなわち
の条件、すなわち
![]()
を用いて(![]() )、解を1つに絞ることに注意してください。
)、解を1つに絞ることに注意してください。
●いま2次系(2重積分器)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \boxed{\left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] = \left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] + \left[\begin{array}{c} 0 \\ 1 \end{array}\right] u(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4872e6ab89edfca755c552863cc2bd93_l3.png)
を安定化する状態フィードバック![]() を,評価関数
を,評価関数
![]()
を最小にするように求めると
![]()
となります。実際、リッカチ方程式
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right] + \left[\begin{array}{cc} 0 & 0 \\ 1 & 0 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]\\ - \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{c} 0 \\ 1 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] + \left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right]\\ = \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d28749ac5a43f35cf85d06d327748bb5_l3.png)
を要素ごとに整理して
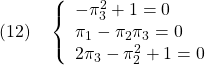
を得る。これは,まず第1式より![]() が2つ,つぎに第3式より
が2つ,つぎに第3式より![]() が2つ,さらに第2式より
が2つ,さらに第2式より![]() が1つ定まり,つぎのように4組の解をもつ。すなわち
が1つ定まり,つぎのように4組の解をもつ。すなわち
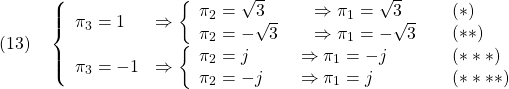
ここで,(*)だけが,![]() を満たします。したがって
を満たします。したがって
![]()
例題1 2次系(無定位系)
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \boxed{\left\{\begin{array}{l} %\underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] %}_{\dot{x}(t)} = %\underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & -2\zeta\omega_n \end{array}\right] %}_{A} %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] + %\underbrace{ \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] %}_{B} \\ y(t)= %\underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] %}_{C} %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] \end{array}\right.} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4804d9477777bd149c8abe1925ce71fe_l3.png)
を安定化する状態フィードバック![]() を,評価関数
を,評価関数
![]()
を最小にするように求めると
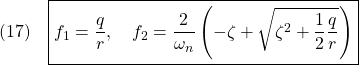
また
![]()
を最小にするように求めると
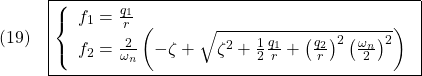
例題2 2次系
![Rendered by QuickLaTeX.com \displaystyle{(20)\quad \boxed{\left\{\begin{array}{l} %\underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] %}_{\dot x} = %\underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] %}_{A} %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] %}_{x} + %\underbrace{ \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] %}_{B} u(t) \\ y(t)= %\underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] %}_{C} %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] \end{array}\right.} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cff43f0c2dd25afe220d33c00beba1c3_l3.png)
を安定化する状態フィードバック![]() を,評価関数
を,評価関数
![]()
を最小にするように求めると
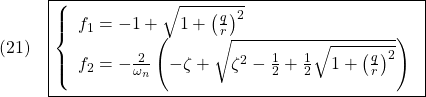
また
![]()
を最小にするように求めると
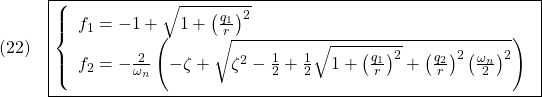
[3] 計算機でリッカチ方程式解くには、ハミルトン行列と呼ばれる
![Rendered by QuickLaTeX.com \displaystyle{(23)\quad \boxed{M=\left[\begin{array}{cc} A & -BR^{-1}B^T \\ C^TQC & -A^T \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7eb0ba79a865b0a2499ee0421c036a1b_l3.png)
を考えます。このハミルトン行列の固有値は、実軸に対称ばかりでなく、虚軸にも対称となるという性質を持っています。これらのうち安定な固有値と対応する固有ベクトルを、次のように求めます。
![Rendered by QuickLaTeX.com \displaystyle{(24)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc} A & -BR^{-1}B^T \\ -C^TQC & -A^T \end{array}\right]}_{M(2n\times 2n)} \underbrace{ \left[\begin{array}{c} V_1 \\ V_2 \end{array}\right]}_{V^-(2n\times n)}\\ = \underbrace{ \left[\begin{array}{c} V_1 \\ V_2 \end{array}\right]}_{V^-(2n\times n)} \underbrace{ {\rm diag}\{\lambda_1,\cdots,\lambda_n\} }_{\Lambda^-(n\times n)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f8a2558fcebdca5d42752fab2101867b_l3.png)
これから
![]()
のように求められます。
●ハミルトン行列を経由してリッカチ方程式解くためのコードは次のようになります。
| MATLAB |
|
| SCILAB |
|
MATLABでは、関数lqrがリッカチ方程式解くために準備されています。
演習A52…Flipped Classroom
![]()
![]()
Note A52-1 行列による微分
いま、任意の行列![]() の
の![]() 要素を
要素を![]() で表すとき、スカラ関数
で表すとき、スカラ関数![]() を行列変数
を行列変数![]() の各要素で微分して得られる行列を
の各要素で微分して得られる行列を![]() で定義します。このとき、行列のトレースについて、次が成り立ちます。
で定義します。このとき、行列のトレースについて、次が成り立ちます。
![]()
![]()
![]()
![]()
実際、
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Note A52-2 LQ制御問題の解法
可制御かつ可観測な![]() 次系
次系
![]()
に対する状態フィードバック
![]()
による閉ループ系
![]()
に対して、評価関数
![]()
を最小化するように![]() を決める問題を考えます。
を決める問題を考えます。
閉ループ系における状態の振る舞いは次式で与えられます。
![]()
ここで、1次系の場合は初期状態は![]() であればよかったのですが、一般の場合はインパルス応答となるように
であればよかったのですが、一般の場合はインパルス応答となるように![]() の列ベクトル
の列ベクトル![]() を考えます。各インパルス応答
を考えます。各インパルス応答
![]()
に対する評価関数![]() の総和は
の総和は
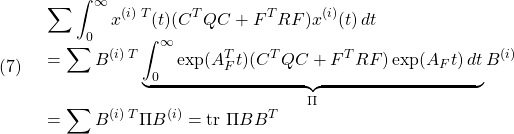
と書けます。いま![]() をラグランジュの未定定数として
をラグランジュの未定定数として
![]()
を最小化する問題を考えます。ここで、制約条件は、リャプノフ方程式と呼ばれる
![]()
ですが、![]() は
は![]() が安定行列を意味することに注意します。
が安定行列を意味することに注意します。
そこで、必要条件として次を得ます。
![]()
![]()
![]()
ここで、第2式から得られる![]() を第3式に代入して
を第3式に代入して
![]()
すなわち、リッカチ方程式と呼ばれる![]() の行列方程式
の行列方程式
![]()
を得ます。これから![]() を求めて、
を求めて、![]() は
は
![]()
のように得られます。このような制御方式をLQ制御と呼びます。
一方、十分性の議論は次のように行われます。まず、被積分項は次のように表すことができます。
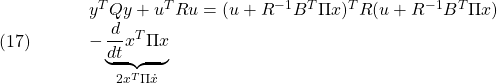
実際、右辺に![]() を代入し、リッカチ方程式を用いると
を代入し、リッカチ方程式を用いると
![]()
したがって、上記の両辺を積分して
![]()
を得ます。ここで、![]() を前提とするので
を前提とするので
![]()
を得ます。これから![]() が評価関数を最小化することが分かります。
が評価関数を最小化することが分かります。
Note A53-3a 例題1(17)の導出
リッカチ方程式
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \\ 0 & -2\zeta\omega_n \end{array}\right] + \left[\begin{array}{cc} 0 & 0 \\ 1 & -2\zeta\omega_n \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]\\ - \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] r^{-2} \left[\begin{array}{cc} 0 & \omega_n^2 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]\\ + \left[\begin{array}{c} 1 \\ 0 \end{array}\right] q^{2} \left[\begin{array}{cc} 1 & 0 \end{array}\right] % \left[\begin{array}{cc} % q_1^2 & 0 \\ % 0 & q_2^2 % \end{array}\right] = \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e43567c4046c4807bb16901e4c9095c1_l3.png)
を要素ごとに整理して
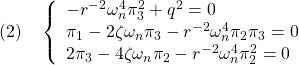
を得る。まず,第1式より![]() が
が
![]()
と求まる。つぎに,第3式より![]() は
は
![]()
となるが,![]() より
より
![]()
でなければならない。さらに,第2式より![]() は
は
![]()
となる(![]() )。すなわち(1)の解として
)。すなわち(1)の解として
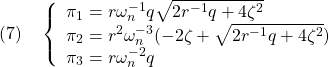
を得ます(このとき![]() も満足されます)。したがって
も満足されます)。したがって
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \left[\begin{array}{cc} f_1 & f_2 \end{array}\right]=r^{-2} \left[\begin{array}{cc} 0 & \omega_n^2 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]=r^{-2}\omega_n^2 \left[\begin{array}{cc} \pi_3 & \pi_2 \end{array}\right]\\ = \left[\begin{array}{cc} \frac{q}{r} & \frac{2}{\omega_n}\left(-\zeta+\sqrt{\zeta^2+\frac{1}{2}\frac{q}{r}}\right) \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ac9df3a510b53e5194c148972b29d62f_l3.png)
Note A53-3b 例題1(19)の導出
リッカチ方程式
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \\ 0 & -2\zeta\omega_n \end{array}\right] + \left[\begin{array}{cc} 0 & 0 \\ 1 & -2\zeta\omega_n \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]\\ - \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] r^{-2} \left[\begin{array}{cc} 0 & \omega_n^2 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]\\ + \left[\begin{array}{cc} q_1^2 & 0 \\ 0 & q_2^2 \end{array}\right] = \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ddd699d8aac23ef2a497f48ee1ecff2d_l3.png)
を要素ごとに整理して、上と同様にして導出されます。
Note A52-3c 例題2(21)の導出
リッカチ方程式
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{ll} \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] + \left[\begin{array}{cc} 0 & -\omega_n^2 \\ 1 & -2\zeta\omega_n \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]\\ - \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] r^{-2} \left[\begin{array}{cc} 0 & \omega_n^2 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]\\ + \left[\begin{array}{c} 1 \\ 0 \end{array}\right] q^2 \left[\begin{array}{cc} 1 & 0 \end{array}\right] = \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right] \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2773454b3e211d96ee83363fb88da2a2_l3.png)
を要素ごとに整理して
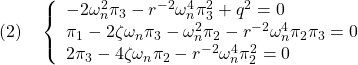
を得る。まず,第1式より![]() が
が
![]()
と求まる。つぎに,第3式より![]() は
は
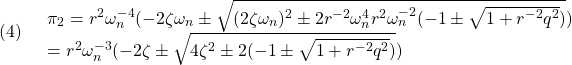
となるが,![]() より
より
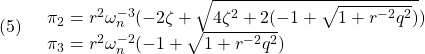
でなければならない。さらに,第2式より![]() は
は
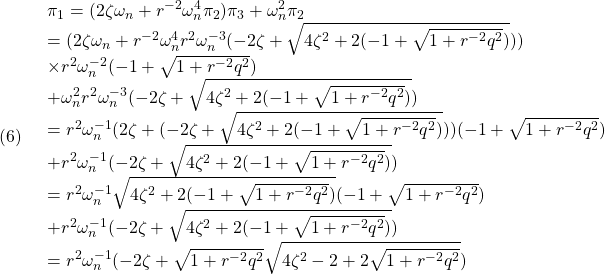
となる(![]() )。すなわち(1)の解として
)。すなわち(1)の解として
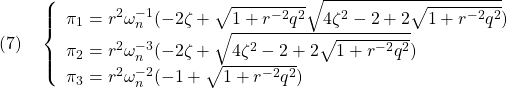
を得ます(このとき![]() も満足されます)。したがって
も満足されます)。したがって
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \left[\begin{array}{cc} f_1 & f_2 \end{array}\right]=r^{-2} \left[\begin{array}{cc} 0 & \omega_n^2 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]=r^{-2}\omega_n^2 \left[\begin{array}{cc} \pi_3 & \pi_2 \end{array}\right]\\ = \left[\begin{array}{cc} -1+\sqrt{1+\left(\frac{q}{r}\right)^2} & -\frac{2}{\omega_n}\left(-\zeta+\sqrt{\zeta^2-\frac{1}{2}+\frac{1}{2}\sqrt{1+\left(\frac{q}{r}\right)^2}}\right) \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b52bac7cab88d375a41fa037afb2d31a_l3.png)
Note A52-3d 例題2(22)の導出
リッカチ方程式
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] + \left[\begin{array}{cc} 0 & -\omega_n^2 \\ 1 & -2\zeta\omega_n \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]\\ - \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] r^{-2} \left[\begin{array}{cc} 0 & \omega_n^2 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]\\ + \left[\begin{array}{cc} q_1^2 & 0 \\ 0 & q_2^2 \end{array}\right] = \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e85a2fc5c10628fc6c41a4d64cd73e6c_l3.png)
を要素ごとに整理して、上と同様にして導出されます。
補遺 上述の議論では、次についての検討が必要です。
検討事項1 (9)の妥当性