CT12 速度制御 | 制御系CAD

Home Work 1.2

[M]　制御則が(1.5)に変わっているけど、(1.1)に代入すると

$\displaystyle{(1)\quad m\dot{v}(t)=k(v_c-v(t)) }$

左辺を右辺に移して

$\displaystyle{(2)\quad m\underbrace{\frac{d}{dt}(v_c-v(t))}_{\dot{e}(t)}+k\underbrace{(v_c-v(t))}_{e(t)}=0 }$

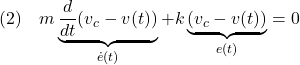
と書けるね。停止制御の場合の $m\dot{v}(t)+kv(t)=0$ において、 $v(t)$ が偏差 $e(t)$ に変わったとみなせま～す。

[P]　ここでも(1.5)をどうやって発生させるのかと思っていたら、どうもアクチュエータ（制御対象への働きかけを行う装置）の設置が前提になっているようだ。それならわかったよ。

[C]　センサ（制御対象の情報収集装置）の設置も前提となっているようだ。すなわち、図1.3のように、センサで検出した信号 $v(t)$ を、アクチュエータに戻す仕組みが考えられており、これをフィードバックと呼ぶらしい。特に偏差 $e(t)=v_c-v(t)$ を作るときに、検出した信号 $v(t)$ にマイナスをつけるので、これを強調して、ネガティブ・フィードバックと呼ぶのだそうだ。これを友達に話すと、「制御という魔法をかけるのだからポジティブなフィードバックじゃないの」と来たよ。確かにそうだけど「ポジティブなフィードバックはネガティブなフィードバックなのだ!?」。

Flipped Classroom 1.2
[1] 　微分方程式を解くにはどの関数を使うのか、また微分方程式をどのように定義するのかに注意してください。　

[2] 　 $v_c$ をいろいろ変えてみてください。将来的には、アニメーションを作成できるとよいですね。次を参考にしてください。

３Ｄアニメーション