|
【本章のねらい】 ・ 状態フィードバックを設計する。 ・ 可制御性と可安定性を判定する。 |
3.1 状態フィードバック
|
いま制御対象は平衡状態にあるとし,何らかの要因でこれが乱されたとき,適当な手段を用いて,速やかに元の平衡状態に戻したい。そのような手段の一つとして,
に対する状態フィードバック
を考える。このとき,(3.2)式を(3.1)式に代入して,閉ループ系
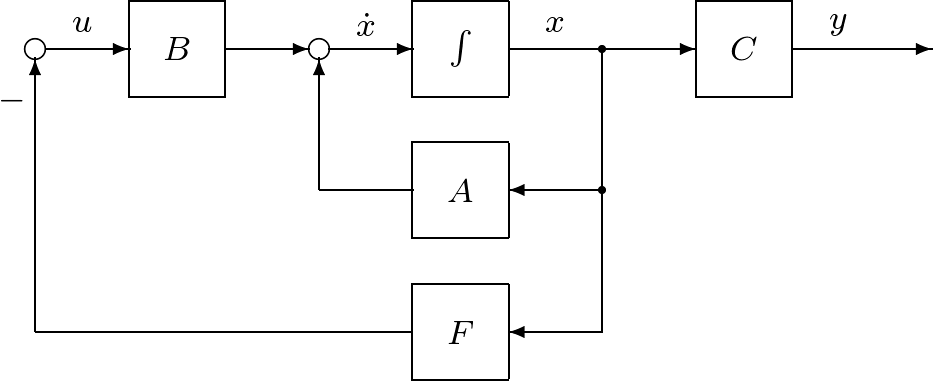
を得る。このブロック線図を次に示す。
上の制御目的が達成されるためには,閉ループ系の (3.4)「任意の が成り立ち,これは平衡状態 まず,1次系の状態フィードバックの例を考える。 例題3.1 時定数
に対して,新しい入力
を行うと閉ループ系の時定数は
となる。これは時定数 演習3.1 1次系 演習3.2 例題2.5で得た図上( つぎに,2次系の状態フィードバックの例を考える。 例題3.2 減衰係数
に対して,新しい入力
を行うと,閉ループ系の減衰係数は
これは減衰係数 演習3.3 例題2.6で得た図上( さて,
また,行列
このとき,閉ループ系の
または
で与えられる(テキスト「線形システム制御入門」の3.3節参照)。(3.8})式と(3.9})式を比較すると,前者は 例題3.3 2次系
に対する状態フィードバック
(1) 行列
したがって,ゲイン行列
(2) 行列
したがって,ゲイン行列
演習3.4 つぎの2次系に対する状態フィードバック (2) 最後に多入力をもつ
ここで
とおくと
これから,
ただし, 例題3.4 2入力2次系
に対するつぎの状態フィードバックによる閉ループ系おける行列 (1) (2)
この特性多項式は
したがって,行列 (2) 閉ループ系の
この特性多項式は
したがって,行列 演習3.5 例題3.4の2つの状態フィードバックは,公式(3.13})において (1) (2) と指定して得られることを,MATLABを用いて確かめよ。 |
3.2 可制御性と可安定性
|
どのような 【可安定性の定義とその等価な条件】 これらの条件の一つが成り立つとき 【可制御性の定義とその等価な条件】 これらの条件の一つが成り立つとき 例題3.5 つぎの (1) (2) (3) 解答 (2) 可制御性行列は, (3) 可制御性行列は, 演習3.6 つぎの (1) (2) MATLABを用いて可制御性を判定するには,たとえば例題3.5(3)の %controllability_check.m ここで,4行目の結果がすべて真であれば,可制御である。 演習3.7 上のコマンドを用いて演習3.6の 例題3.6 例題3.5の
したがって,この2次系は可安定である。 (2)
したがって,この2次系は可安定ではない。 (3)
したがって,この2次系は可安定である。 演習3.8 演習3.6の MATLABを用いて可安定性を判定するには,たとえば例題3.5(3)の %stabilizability_check.m 演習3.9 上のコマンドを用いて演習3.6の |
演習問題の解答
| 演習3.1 演習3.2 たとえば,つぎのMファイルを実行すればよい。 %sf1.m 演習3.3 たとえば,つぎのMファイルを実行すればよい。 %sf2.m 演習3.4 行列
(1) したがって,ゲイン行列
(2)
したがって,ゲイン行列
演習3.5 たとえば,つぎのMファイルを実行すればよい。 %sf_minputs.m 演習3.6 (1) 可制御性行列は, (2) 可制御性行列は, 演習3.7 Mファイル{\tt controllability\_check.m}のデータ{\tt A,B}の定義を次のように書き換える。 (1) A=[0 1 0;0 -1 1;0 0 -1]; B=[0;1;0]; 演習3.8
したがって,この3次系は可安定である。 (2)
したがって,この3次系は可安定である。 演習3.9 Mファイル{\tt stabilizability\_check.m}のデータ{\tt A,B}の定義を,次のように書き換える。 (1) A=[0 1 0;0 -1 1;0 0 -1]; B=[0;1;0]; |
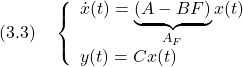
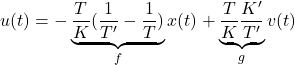
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] }_{\dot x} = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] }_{x} + \underbrace{ \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] }_{B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5932569bcea6f83e90d462d598332ff4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ u(t)=- \underbrace{ \left[\begin{array}{cc} \frac{1}{\omega_n^2}(\omega_n'\,^2-\omega_n^2) & \frac{2}{\omega_n^2}(\zeta'\omega_n'-\zeta\omega_n) \end{array}\right] }_{F} \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] +\underbrace{\frac{\omega_n'\,^2}{\omega_n^2}}_Gv(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-265415e99e8b4aed32c5f7a8ce5fbc90_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{lll} &&A-BF= \left[\begin{array}{cc} 0 & 1 \\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] - \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right]\\ && \times \left[\begin{array}{cc} \frac{1}{\omega_n^2}(\omega_n'\,^2-\omega_n^2) & \frac{2}{\omega_n^2}(\zeta'\omega_n'-\zeta\omega_n) \end{array}\right] =\left[\begin{array}{cc} 0 & 1 \\ -\omega_n'\,^2 & -2\zeta'\omega_n' \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f0d26f2790cc8788d788deb679fa2869_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3.8)\quad \begin{array}{lll} F&=&\left[\begin{array}{cccc} a_n'-a_n & \cdots & a_2'-a_2 & a_1'-a_1 \end{array}\right] \nonumber\\ &\times& \left[\begin{array}{ccccc} a_{n-1} & a_{n-2} & \cdots & a_1 & 1 \\ a_{n-2} & a_{n-3} & \cdots & 1 & 0 \\ \vdots & \vdots & \cdots & \vdots & \vdots \\ a_2 & a_1 & \cdots & 0 & 0 \\ a_1 & 1 & \cdots & 0 & 0 \\ 1 & 0 & \cdots & 0 & 0 \end{array}\right]^{-1} \nonumber\\ &\times& \left[\begin{array}{cccc} B & AB &\cdots & A^{n-1}B \end{array}\right]^{-1} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-76067715bdbc7d9b8029b271b91a27de_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \\ \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} {x}_1(t) \\ {x}_2(t) \\ \end{array}\right] }_{{x}(t)}+ \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f8bc98dd7c81e82779b6017dbc6cb85e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ {\rm det}(\lambda I_2-A)= {\rm det}\left[\begin{array}{cc} \lambda & -1 \\ 0 & \lambda \end{array}\right] =\lambda^2+\underbrace{0}_{a_1}\lambda+\underbrace{0}_{a_2} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4a8163de84bd0261dff1fa933592b34c_l3.png)
![Rendered by QuickLaTeX.com \underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \\ \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & -1 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} {x}_1(t) \\ {x}_2(t) \\ \end{array}\right] }_{{x}(t)}+ \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B} u(t)](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9040963fdd9acf7b39f1bf812fa99c88_l3.png)
![Rendered by QuickLaTeX.com \underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \\ \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -1 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} {x}_1(t) \\ {x}_2(t) \\ \end{array}\right] }_{{x}(t)}+ \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B} u(t)](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f5aff16fd9935d4b51dc9dea0f54e64b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \\ \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 0 \\ 0 & -1 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} {x}_1(t) \\ {x}_2(t) \\ \end{array}\right] }_{{x}(t)}+ \underbrace{ \left[\begin{array}{cc} 1 & 1 \\ 1 & -1 \end{array}\right] }_{B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5b7a0db163b44996055239c4cf8ec6aa_l3.png)
![Rendered by QuickLaTeX.com u(t)=- \underbrace{ \left[\begin{array}{cc} 1 & 1 \\ 1 & -1 \end{array}\right] }_{F} \underbrace{ \left[\begin{array}{c} {x}_1(t) \\ {x}_2(t) \\ \end{array}\right] }_{{x}(t)}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8a1880804ad575edaa4ce349005ec561_l3.png)
![Rendered by QuickLaTeX.com u(t)=- \underbrace{ \left[\begin{array}{cc} 1 & 0 \\ 1 & -2 \end{array}\right] }_{F} \underbrace{ \left[\begin{array}{c} {x}_1(t) \\ {x}_2(t) \\ \end{array}\right] }_{{x}(t)}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d7681a2997f575f972ebd16c2a6cf272_l3.png)
![Rendered by QuickLaTeX.com A= \left[\begin{array}{ccc} 0 & 1 & 0 \\ 0 & -1 & 1 \\ 0 & 0 & -1 \end{array}\right] ,\ B= \left[\begin{array}{c} 0 \\ 1 \\ 0 \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6cc304a4620ea5dad9c5361bc465956f_l3.png)
![Rendered by QuickLaTeX.com A= \left[\begin{array}{ccc} 0 & 1 & 0 \\ -1 & -1 & 0 \\ 0 & 0 & 2 \end{array}\right] ,\ B= \left[\begin{array}{cc} 0 & 0 \\ 1 & -1 \\ 0 & 1 \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f6830e3d13f543452788ce6893c98e2d_l3.png)
![Rendered by QuickLaTeX.com {\rm det}(\lambda I_2-A)= {\rm det}\left[\begin{array}{cc} \lambda & -1 \\ 0 & \lambda+1 \end{array}\right] =\lambda(\lambda+1) =\lambda^2+\underbrace{1}_{a_1}\lambda+\underbrace{0}_{a_2}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-65acea39d75710f02f1e7c20e6043964_l3.png)
![Rendered by QuickLaTeX.com {\rm det}(\lambda I_2-A)= {\rm det}\left[\begin{array}{cc} \lambda & -1 \\ 1 & \lambda \end{array}\right] =\lambda^2+1 =\lambda^2+\underbrace{0}_{a_1}\lambda+\underbrace{1}_{a_2}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3d9ad5dbdcf90b601c9c329ce2b16c08_l3.png)
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc} B & AB & A^2B \end{array}\right]= \left[\begin{array}{ccc} 0 & 1 & -1 \\ 1 & -1 & 1 \\ 0 & 0 & 0 \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-067a828760d4077d69d7af72f096c285_l3.png) 。この階数は2で,システムの次数3より小さい。したがって,この3次系は不可制御である。
。この階数は2で,システムの次数3より小さい。したがって,この3次系は不可制御である。![Rendered by QuickLaTeX.com \left[\begin{array}{ccc} B & AB & A^2B \end{array}\right]= \left[\begin{array}{cccccc} 0 & 0 & 1 &-1 &-1 & 1\\ 1 &-1 &-1 & 1 & 0 & 0\\ 0 & 1 & 0 & 2 & 0 & 4 \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b6489685f970d758a91f786a979180de_l3.png) 。この階数は3で,システムの次数3と等しい。
。この階数は3で,システムの次数3と等しい。![Rendered by QuickLaTeX.com {\rm rank} \left[\begin{array}{cc} B & A-\lambda_1 I_3 \end{array}\right]= {\rm rank} \left[\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 1 & 0 & -1 & 1 \\ 0 & 0 & 0 & -1 \end{array}\right]= 3](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8ac387d8c9e926e0876ad2511344ba70_l3.png)
![Rendered by QuickLaTeX.com {\rm rank} \left[\begin{array}{cc} B & A-\lambda_3 I_3 \end{array}\right]= {\rm rank} \left[\begin{array}{ccccc} 0 & 0 & -2 & 1 & 0 \\ 1 & -1 & 0 & -2 & 1 \\ 0 & 1 & 0 & 0 & -2 \end{array}\right]= 3](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-24936c92a1e90e689dc378bb582c938c_l3.png)