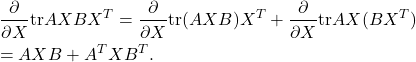1. Optimal Control for MIMO system
![]() Given an nth-order system (satisfying controllability and observability)
Given an nth-order system (satisfying controllability and observability)
(1) ![]()
and the stabilizing state feedback
(2) ![]()
the closed-loop system is represented by
(3) 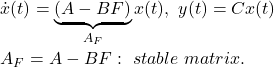
The behaviors of the state and the input are given by
(4) ![]()
and
(5) ![]()
respectively. Then consider a problem to determine ![]() to minimize the criterion function
to minimize the criterion function
(6) ![]()
![]() The criterion function can be written as
The criterion function can be written as
(7) 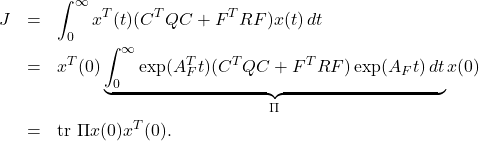
Note that we have the following constraint on ![]() :
:
(8) ![]()
It is known that ![]() holds because of the closed-loop stability. Taking account of all zero-input responses, instead of (7), we consider to minimize
holds because of the closed-loop stability. Taking account of all zero-input responses, instead of (7), we consider to minimize
(9) ![]()
Therefore, we will minimize
(10) ![]()
using undetermined multiplier ![]() and the stability constraint (8). As the necessary conditions, we have
and the stability constraint (8). As the necessary conditions, we have
(11) ![]()
(12) ![]()
(13) ![]()
Substituting ![]() into (13),
into (13),
(14) ![]()
That is, we have the Algebraic Riccati Equation (ARE) on ![]() :
:
(15) ![]()
By solving this, we can obtain ![]() and then
and then ![]() by
by
(16) ![]()
The control methodology is called as LQ Control.
![]() The sufficiency is discussed as follows. The following expression can be derived:
The sufficiency is discussed as follows. The following expression can be derived:
(17) 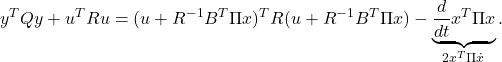
In fact, substituting ![]() into the right hand side and using the Riccati equation,
into the right hand side and using the Riccati equation,
(18) ![]()
Integrating the both side,
(19) ![]()
As ![]() ,
,
(20) ![]()
Therefore, it is shown that ![]() minimizes the criterion function.
minimizes the criterion function.
Exercise 1
Given ![]() , obtain the solution
, obtain the solution ![]() of the Riccati equation
of the Riccati equation ![]() and calculate
and calculate ![]() .
.
Expanding the Ricatti equation
(21) ![Rendered by QuickLaTeX.com \begin{eqnarray*} && \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right] + \left[\begin{array}{cc} 0 & 0 \\ 1 & 0 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \nonumber\\ &&-\left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{c} 0 \\ 1 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] + \left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right] = \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right] \nonumber , \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8451bf77f93103b4b977badfda8b557b_l3.png)
we have
(22) 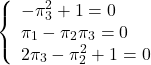
There are the two solutions on ![]() from
from ![]() , the two solutions on
, the two solutions on ![]() from
from ![]() , the one solution
, the one solution ![]() from
from ![]() . Therefore, we have the four kinds of solution
. Therefore, we have the four kinds of solution ![]() as follows:
as follows:
(23) 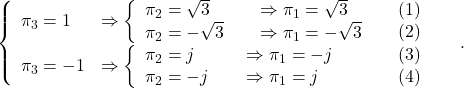
The only (1) satisfies ![]() . Therefore we have
. Therefore we have
(24) ![]()
●How to solve ARE
Given the Riccati equation ![]() , consider the Hamilton matrix
, consider the Hamilton matrix
(25) ![]()
The eigenvalues of the Hamilton matrix with size ![]() are distributed symmetrically to not only the real axis but also the imaginal axis. So there are
are distributed symmetrically to not only the real axis but also the imaginal axis. So there are ![]() stable eigenvalues and
stable eigenvalues and ![]() unstable eigenvalues. The eigenvectors corresponding to
unstable eigenvalues. The eigenvectors corresponding to ![]() stable eigenvalues
stable eigenvalues ![]() are obtained as follows:
are obtained as follows:
(26) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \underbrace{ \left[\begin{array}{cc} A & -BR^{-1}B^T \\ -C^TQC & -A^T \end{array}\right]}_{M(2n\times 2n)} \underbrace{ \left[\begin{array}{c} V_1 \\ V_2 \end{array}\right]}_{V^-(2n\times n)} = \underbrace{ \left[\begin{array}{c} V_1 \\ V_2 \end{array}\right]}_{V^-(2n\times n)} \underbrace{ {\rm diag}\{\lambda_1,\cdots,\lambda_n\} }_{\Lambda^-(n\times n)}. \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6134fe44b7b15f5c2ed017d856889b8b_l3.png)
Based on this, we can obtain ![]() as
as
(27) ![]()
A program by SCILAB to solve the Riccati equation is given as follows.
//opt.sce
function [F,p]=opt(A,B,C,Q,R)
W=R\B’; [V,R]=spec([A -B*W;-C’*Q*C -A’]);
p=diag(R); [dummy,index]=gsort(real(p));
n=size(A,1); j=index(n+1:n+n);
p=p(j); V1=V(1:n,j); V2=V(n+1:n+n,j);
X=real(V2/V1); F=W*X;
endfunction
//eof
Solve the Riccati equation in Exercise 1 by using the above program.
A=[0 1;0 0]; B=[0;1]; C=eye(2,2);
Q=diag([1 1]); R=1;
[F,p]=opt(A,B,C,Q,R)
poles=spec(A-B*F)
Exercise 2
Consider the following spring-connected carts as a control object.
The motion is governed by
(28) ![]()
where ![]() is a spring constant with the range
is a spring constant with the range ![]() . The state equation and output equation are given by
. The state equation and output equation are given by
(29) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \\ \ddot{x}_1(t) \\ \ddot{x}_2(t) \\ \end{array}\right] }_{\dot{x}(t)} &=& \underbrace{ \left[\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ -\frac{k}{m_1} & -\frac{k}{m_1} & 0 & 0 \\ \frac{k}{m_2} & -\frac{k}{m_2}& 0 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} {x}_1(t) \\ {x}_2(t) \\ \dot{x}_1(t) \\ \dot{x}_2(t) \\ \end{array}\right] }_{x(t)}\\ &&+ \underbrace{ \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \\ \frac{k}{m_1} & 0 \\ 0 & \frac{k}{m_2} \end{array}\right] }_{B} \underbrace{ \left[\begin{array}{c} f_1(t) \\ f_2(t) \end{array}\right] }_{u(t)}, \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2d4ea85cc25cd0f7c8c3404af6ff3979_l3.png)
(30) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] }_{y(t)} &=&- \underbrace{ \left[\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} {x}_1(t) \\ {x}_2(t) \\ \dot{x}_1(t) \\ \dot{x}_2(t) \\ \end{array}\right] }_{x(t)}. \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-611550582beb0b3ed91eb51c1a672f96_l3.png)
The control purpose is to regulate the zero-input response under the initial condition:
(31) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \left[\begin{array}{c} {x}_1(0) \\ {x}_2(0) \\ \dot{x}_1(0) \\ \dot{x}_2(0) \\ \end{array}\right] = \left[\begin{array}{c} 0 \\ 0 \\ 0 \\ \frac{k}{m_2} \end{array}\right] \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c3699ab4b4d4527cb552796332d8087f_l3.png)
by using the state feedback:
(32) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \underbrace{ \left[\begin{array}{c} f_1(t) \\ f_2(t) \end{array}\right] }_{u(t)} &=&- \underbrace{ \left[\begin{array}{cccc} g_{11} & g_{12} & g_{13} & g_{14} \\ g_{21} & g_{22} & g_{23} & g_{24} \end{array}\right] }_{F} \underbrace{ \left[\begin{array}{c} {x}_1(t) \\ {x}_2(t) \\ \dot{x}_1(t) \\ \dot{x}_2(t) \\ \end{array}\right] }_{x(t)}. \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-534b70a7ee454caba7d663c5dba90e8f_l3.png)
In order to determine the state feedback gain ![]() , for
, for ![]() fixed to an appropriate nominal value
fixed to an appropriate nominal value ![]() , we will minimize the following criterion function:
, we will minimize the following criterion function:
(33) ![]()
that is
(34) ![Rendered by QuickLaTeX.com \begin{eqnarray*} J&=&\int_0^\infty ( \underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right]^T }_{y^T(t)} \underbrace{ \left[\begin{array}{cc} q_1^2 & 0 \\ 0 & q_2^2 \ \end{array}\right] }_{Q} \underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] }_{y(t)}\\ &&+\underbrace{ \left[\begin{array}{c} f_1(t) \\ f_2(t) \end{array}\right]^T }_{u^T(t)} \underbrace{ \left[\begin{array}{cc} r_1^2 & 0 \\ 0 & r_2^2 \ \end{array}\right] }_{R} \underbrace{ \left[\begin{array}{c} f_1(t) \\ f_2(t) \end{array}\right] }_{u(t)} )\,dt. \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e39ecdd42eaf2ef9fcad46841e42ca20_l3.png)
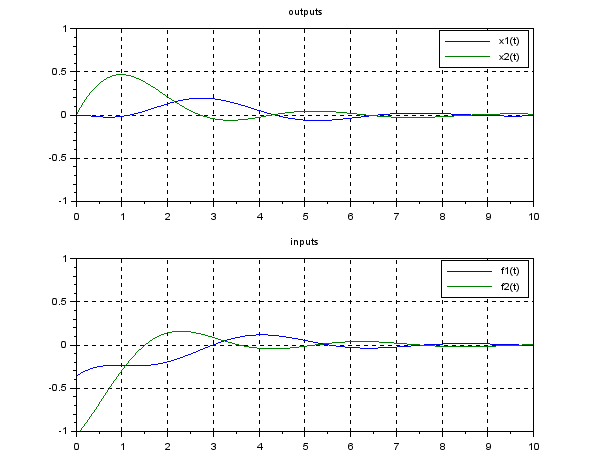
For example, the closed-loop zero-input response is simulated under the following assumptions:
1) ![]() ,
, ![]() ,
, ![]() ,
,
2) ![]() ,
, ![]() ,
, ![]() ,
, ![]()
(![]() ).
).
Appendix 1
Check the following properties on matrix trace.
(35) ![]()
(36) ![]()
(37) ![]()
(38) ![]()
where ![]() for
for ![]() . In fact,
. In fact,
(39) ![]()
(40) ![Rendered by QuickLaTeX.com \begin{eqnarray*} &&[\frac{\partial}{\partial X}{\rm tr}AXB]_{ij} =\frac{\partial}{\partial x_{ij}}\sum_{k}[AXB]_{kk} =\frac{\partial}{\partial x_{ij}}\sum_{k}\sum_{i,j}a_{ki}x_{ij}b_{jk}\\ &&=\sum_{k}b_{jk}a_{ki}=[BA]_{ji}=[A^TB^T]_{ij}, \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-05455a1f26f5ab87bf6b1f0503ea4df8_l3.png)
(41) ![Rendered by QuickLaTeX.com \begin{eqnarray*} &&[\frac{\partial}{\partial X}{\rm tr}AX^TB]_{ij} =\frac{\partial}{\partial x_{ij}}\sum_{k}[AX^TB]_{kk} =\frac{\partial}{\partial x_{ij}}\sum_{k}\sum_{i,j}a_{ki}x_{ji}b_{jk}\\ &&=\sum_{k}b_{ik}a_{kj}=[BA]_{ij}, \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-98102e722ac70c87430ce9f0a0f5f96a_l3.png)
(42)