1. Optimal Control for a SISO system
Given a 1st-order system with an input and an output:
(1) ![]()
and its stabilizing state feedback:
(2) ![]()
the closed-loop system is represented by
(3) ![]()
The state behavior ![]() and the input behavior
and the input behavior ![]() are given by
are given by
(4) ![]()
and
(5) ![]()
respectively. Then consider a problem to determine ![]() to minimize a criterion function
to minimize a criterion function
(6) ![]()
The first term of the criterion function is calculated as
(7) ![Rendered by QuickLaTeX.com \begin{eqnarray*} J_x&=&\int_0^\infty q^2x^2(t)\,dt \nonumber\\ &=&\int_0^\infty q^2e^{2(a-bf)t}x^2(0)\,dt \nonumber\\ &=&q^2x^2(0)\left[\frac{1}{2(a-bf)}e^{2(a-bf)t}\right]_0^\infty \nonumber\\ &=&\frac{q^2x^2(0)}{2(a-bf)}\left[\underbrace{e^{2(a-bf)\infty}}_{0}-\underbrace{e^{2(a-bf)0}}_{1}\right] \nonumber\\ &=&-\frac{q^2}{2(a-bf)}x^2(0)>0\quad (a-bf<0), \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7559be4064d055fb7cda05e82615d8a7_l3.png)
and the second term of the criterion function is calculated as
(8) ![Rendered by QuickLaTeX.com \begin{eqnarray*} J_u&=&\int_0^\infty r^2u^2(t)\,dt \nonumber\\ &=&\int_0^\infty r^2f^2e^{2(a-bf)t}x^2(0)\,dt \nonumber\\ &=&r^2f^2x^2(0)\left[\frac{1}{2(a-bf)}e^{2(a-bf)t}\right]_0^\infty \nonumber\\ &=&-\frac{r^2f^2}{2(a-bf)}x^2(0)>0\quad (a-bf<0). \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cc45ca8495790c6bd637a24e40a72189_l3.png)
Therefore, the criterion function can be written as
(9) 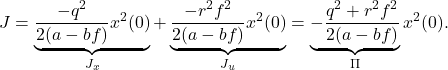
Minimizing ![]() is equivalent to minimizing
is equivalent to minimizing
(10) ![]()
Differentiating by ![]() brings
brings
(11) 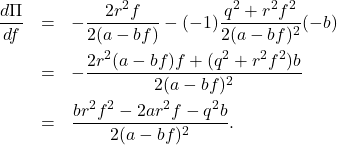
Therefore
(12) ![]()
As ![]() must satisfy
must satisfy ![]() , we have
, we have
(13) 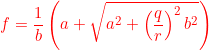
This is uniquely determined because ![]() is downward convex as follows:
is downward convex as follows:
(14) 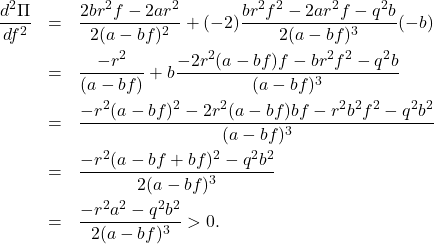
The closed-loop system by the ![]() is given by
is given by
(15) ![]()
In the case of ![]() ,
,
(16) 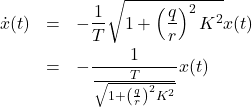
which means that the new time constant is shorter than the original time constant ![]() .
.
Exercise 1
Letting ![]() ,
, ![]() ,
, ![]() , consider the following cases:
, consider the following cases:
Case#1: ![]()
Case#2: ![]()
Case#3: ![]()
Then simulate the behaviors of ![]() and
and ![]() as follows.
as follows.
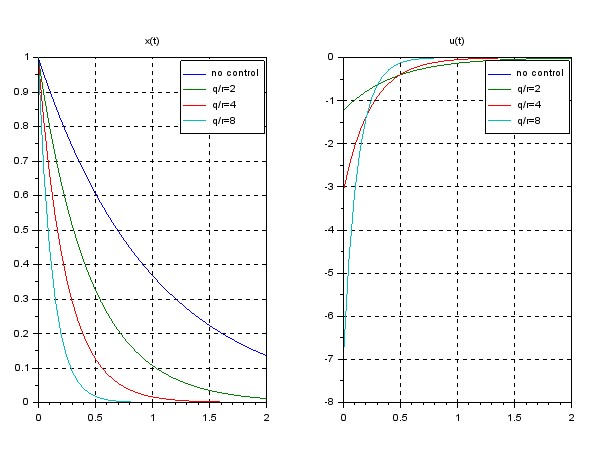
Question:
Why do we use not only ![]() but also
but also ![]() in the criterion function.
in the criterion function.
Answer:
Check that ![]() is downward convex, and takes the minimum value at
is downward convex, and takes the minimum value at ![]() as follows:
as follows:
(17) 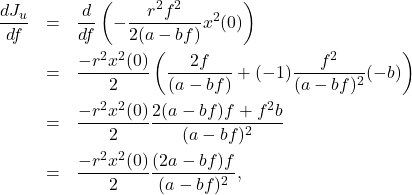
(18) 
For example, letting ![]() , for
, for ![]() and
and ![]() , the overview of
, the overview of ![]() ,
, ![]() ,
, ![]() are drown as follows.
are drown as follows.
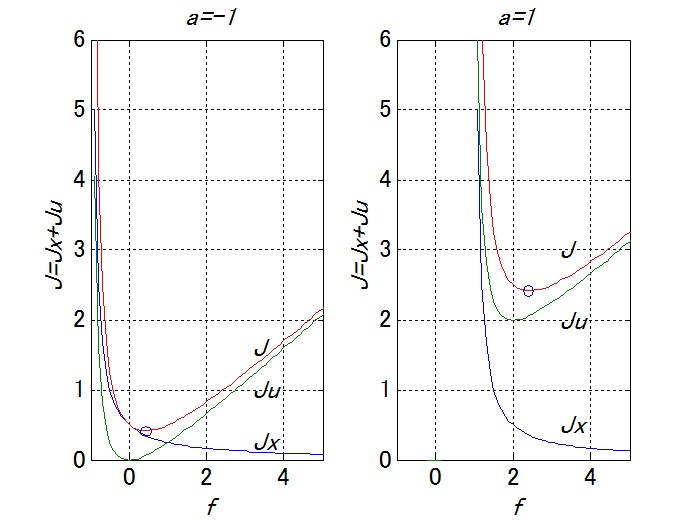
Here the symbol “o” shows the minimum of ![]() . Note that
. Note that ![]() is necessary to make
is necessary to make ![]() downward convex.
downward convex.
Appendix
In order to extend the above discussion to MIMO systems, we should be familiar with Lagrange’s method of undetermined multipliers. We will rewrite the above discussion by using this method as follows.
From (10), note that the constraint on ![]() is given by the following Lyapnov’s equation
is given by the following Lyapnov’s equation
(19) ![]()
Here ![]() holds because of
holds because of ![]() . Therefore, instead of minimizing
. Therefore, instead of minimizing ![]() , we will minimize
, we will minimize
(20) ![]()
using undetermined multiplier ![]() and the stability constraint (19). As the necessary conditions, we have
and the stability constraint (19). As the necessary conditions, we have
(21) ![]()
(22) ![]()
(23) ![]()
Substituting ![]() into (23),
into (23),
(24) ![]()
That is, we have the second-order equation on ![]()
(25) ![]()
which is called as Ricatti equation. By solving this, ![]() is obtained by
is obtained by
(26) ![]()
and ![]() is given by
is given by
(27) 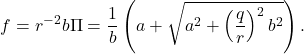
Lastly consider the following matrix:
(28) ![]()
which is called as Hamilton matrix. The stable eigenvalue is given by
(29) ![]()
from
(30) ![]()
The corresponding eigenvector is obtained as
(31) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \left[\begin{array}{cc} v_1 \\ v_2 \end{array}\right] =\left[\begin{array}{cc} 1 \\ \frac{-a-\sqrt{a^2+r^{-2}b^2q^2}}{-r^{-2}b^2} \end{array}\right] \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-054e996fc3498f6cf60565cada2b6d52_l3.png)
Note that
(32) ![]()
and
(33) ![]()