振り子の特性解析

[0]　MAXIMAを用いて、倒立振子の運動方程式を導出し、非線形状態方程式を求め、これを平衡状態まわりで線形化（１次近似）し、線形状態方程式を求めます。

そのために必要となるのが、ベクトル値多変数関数

$\displaystyle{y=f(x)\ (x\in{\rm\bf R}^n,y\in{\rm\bf R}^m)}$

の $x=a(\in{\rm\bf R}^n)$ まわりの１次近似式

$\displaystyle{f(x)\simeq f(a)+\frac{\partial f(a)}{\partial x}(x-a)$

です。これは、たとえば、 $n=m=2$ のとき、次のように計算されます。

$\begin{array}{lll} \underbrace{ \left[\begin{array}{cc} f_1(x_1,x_2)\\ f_2(x_1,x_2) \end{array}\right] }_{f(x)}\nonumber\\ \simeq \left[\begin{array}{cc} f_1(a_1,a_2)+\frac{\partial\,f_1(a_1,a_2)}{\partial\,x_1}(x_1-a_1)+\frac{\partial\,f_1(a_1,a_2)}{\partial\,x_2}(x_2-a_2)\\ f_2(a_1,a_2)+\frac{\partial\,f_2(a_1,a_2)}{\partial\,x_1}(x_1-a_1)+\frac{\partial\,f_2(a_1,a_2)}{\partial\,x_2}(x_2-a_2) \end{array}\right]\nonumber\\ = \underbrace{ \left[\begin{array}{cc} f_1(a_1,a_2)\\ f_2(a_1,a_2) \end{array}\right] }_{f(a)} + \underbrace{ \left[\begin{array}{cc} \frac{\partial f_1(a_1,a_2)}{\partial x_1}&\frac{\partial f_1(a_1,a_2)}{\partial x_2}\\ \frac{\partial f_2(a_1,a_2)}{\partial x_1}&\frac{\partial f_2(a_1,a_2)}{\partial x_2} \end{array}\right] }_{\frac{\partial\,f(a)}{\partial\,x}} \underbrace{ \left[\begin{array}{cc} x_1-a_1\\ x_2-a_2\nonumber \end{array}\right] }_{x-a}\nonumber \end{array}$

[1] 振り子PEN

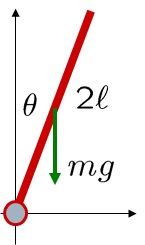
上図の振り子PENを見てください。長さ、 $L=2\ell$ の振り子の重心周りの慣性モーメントは

$\displaystyle{J_0=\int_{-\ell}^{\ell}r^2\,dm=\int_{-\ell}^{\ell}r^2\,\frac{m}{2\ell}dr=\frac{m}{2\ell}\left[\frac{r^3}{3}\right]_{-\ell}^{\ell}=\frac{1}{3}m\ell^2}$

のように計算できます。これから，振り子の軸まわりの慣性モーメントは、平行軸の定理を使って

$\displaystyle{J=\frac{1}{3}m\ell^2+m\ell^2=\frac{4}{3}m\ell^2}$

のように与えられます。また、軸まわりのトルクは

$\displaystyle{\tau=mg\ell\sin\theta}$

のように表わされます。したがって、振り子の運動方程式は、次式となります。

$\displaystyle{J\ddot{\theta}=\tau\ \Rightarrow\ \ddot{\theta}=\frac{3g}{4\ell}\sin\theta}$

それでは、この運動方程式を、ラグランジュの方法で導出してみます。その手順は次のようになります。

まず、振り子の重心のx、y座標と、軸周りの慣性モーメントは

$x=\ell\sin\theta$
$y=\ell\cos\theta$
$J_0=\frac{1}{3}m\ell^2$

ですから、運動エネルギーと位置エネルギーは

$T=\frac{1}{2}m(\dot{x}^2+\dot{y}^2)+\frac{1}{2}J_0\dot{\theta}^2$
$V=mg\ell\cos\theta$

となり、ラクランジアンを

$L=T-V$

として、ラグランジュの運動方程式は

$\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{\theta}}\right)-\frac{\partial L}{\partial\theta}=0$

となります。これから振り子の運動方程式が得られます。

それでは、MAXIMAを用いて、振り子の運動方程式を導出してみましょう。

/*pen.wxm*/
dth:’diff(th(t),t);
ddth:’diff(th(t),t,2);
x:ell*sin(th(t));
y:ell*cos(th(t));
J:(1/3)*m*ell^2;
T:(1/2)*m*(diff(x,t)^2+diff(y,t)^2)+(1/2)*J*dth^2;
V:m*g*ell*cos(th(t));
L:T-V;
LE:diff(diff(L,dth),t)-diff(L,th(t))=0,trigreduce;
sol:solve(LE,ddth);

次に、２階微分を含む運動方程式を１階微分だけの連立微分方程式に変換し、これをベクトル表示します。

$\displaystyle{\ddot{\theta}=\frac{3g}{4\ell}\sin\theta \quad\Leftrightarrow \left\{\begin{array}{l} \dot{\theta}=\omega\\ \dot{\omega}=\frac{3g}{4\ell}\sin\theta \end{array}\right. \quad\Leftrightarrow \left[\begin{array}{c} \dot{\theta} \\ \dot{\omega} \end{array}\right] = \left[\begin{array}{c} \omega \\ \frac{3g}{4\ell}\sin\theta \end{array}\right]}$

すなわち、状態変数ベクトル

$\xi= \left[\begin{array}{c} {\theta} \\ {\omega} \end{array}\right]$

を定義するとき、振り子の非線形状態方程式

$\dot\xi=f(\xi)$

ただし

$f(\xi)= \left[\begin{array}{c} f_1(\xi) \\ f_2(\xi) \end{array}\right] = \left[\begin{array}{c} f_1(\theta,\omega) \\ f_2(\theta,\omega) \end{array}\right] = \left[\begin{array}{c} \omega \\ \frac{3g}{4\ell}\sin\theta \end{array}\right]$

が得られました。ところで、振り子は２つの平衡状態（物理的な釣り合いの状態）を持ちます。

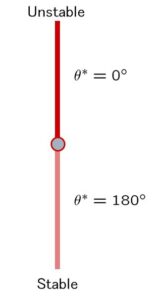
これらは次のように特徴付けられます。

$\dot\xi^*=f(\xi^*)=0$

すなわち

$\underbrace{ \left[\begin{array}{c} \dot{\theta}^* \\ \dot{\omega}^* \end{array}\right] }_{\dot{\xi}^*} = \underbrace{ \left[\begin{array}{c} \omega^* \\ \frac{3g}{4\ell}\sin\theta^* \end{array}\right] }_{f(\xi^*)} = \underbrace{ \left[\begin{array}{c} 0 \\ 0 \end{array}\right] }_{0} \ \Rightarrow\ \xi^* = \left[\begin{array}{c} \theta^* \\ \omega^* \end{array}\right] = \left[\begin{array}{c} 0 \\ 0 \end{array}\right] \,or\, \left[\begin{array}{c} \pi \\ 0 \end{array}\right]$

そこで、振り子の非線形状態方程式を、平衡状態まわりで線形化（１次近似）します。

$\dot{\xi}=f(\xi)\simeq \underbrace{f(\xi^*)}_{\dot{\xi}^*=0} +\frac{\partial f(\xi^*)}{\partial\xi} (\xi-\xi^*)$

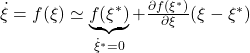
ただし

$\displaystyle{ \frac{\partial f(\xi^*)}{\partial\xi}=\left.\left[\begin{array}{cc} \frac{\partial f_1}{\partial\theta} & \frac{\partial f_1}{\partial\omega} \\ \frac{\partial f_2}{\partial\theta} & \frac{\partial f_2}{\partial\omega} \end{array}\right] \right|_{\theta=\theta^*,\omega=0}}$

これから、振り子の線形状態方程式

$\underbrace{\dot{\xi}-\dot{\xi}^*}_{\dot{x}}= \underbrace{\left.\frac{\partial f(\xi^*)}{\partial\xi}\right.}_A \underbrace{(\xi-\xi^*)}_{x}$

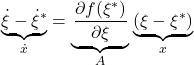
すなわち

$\underbrace{ \frac{d}{dt} \left[\begin{array}{c} \theta-\theta^* \\ \omega-\omega^* \end{array}\right] }_{\dot{x}}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ \frac{3g}{4\ell}\cos\theta^* & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \theta-\theta^* \\ \omega-\omega^* \end{array}\right] }_{x}$

を得ます。以上の計算をMAXIMAを用いて実行するには、次のコマンドを与えます。

f:matrix([dth],[rhs(sol[1])]);
A:matrix([diff(f[1,1],th(t)),diff(f[1,1],dth)],[diff(f[2,1],th(t)),diff(f[2,1],dth)]);
A1:A,th(t)=0;
A2:A,th(t)=%pi;

制御系CAD

制御を意識したモノつくりを目指して

振り子の特性解析