[1] 次の値を計算せよ。
![]()
![]()
[2] 次の関数のグラフを描け。
![]()
[3] つぎの行列![]() の逆行列
の逆行列![]() を計算し、
を計算し、![]() を確認せよ。
を確認せよ。
![]()
[4] 次のA行列の固有値を計算せよ。![]() を解け。
を解け。
![]()
[5] ![]() において、
において、![]() 、
、![]() のとき、
のとき、![]() の固有値が{-1,-2}となるように状態フィードバック
の固有値が{-1,-2}となるように状態フィードバック![]() を、次式によって定めよ。また、その妥当性を
を、次式によって定めよ。また、その妥当性を![]() の固有値を計算して確かめよ。
の固有値を計算して確かめよ。
![]()
ヒント:多項式![]() の係数
の係数![]() と
と![]() はそれぞれcoeff(p,s,1)とcoeff(p,s,0)で与えられる。
はそれぞれcoeff(p,s,1)とcoeff(p,s,0)で与えられる。
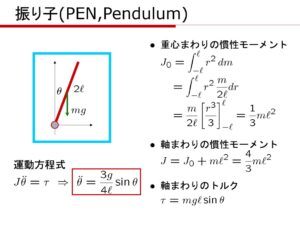
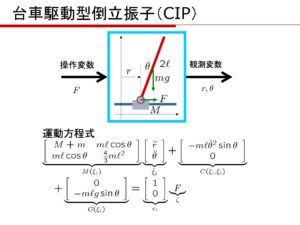
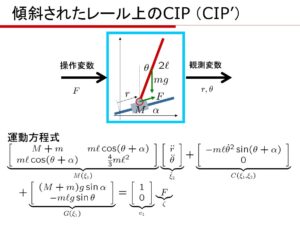
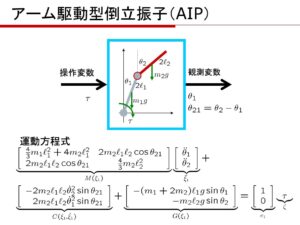
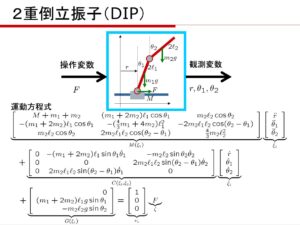
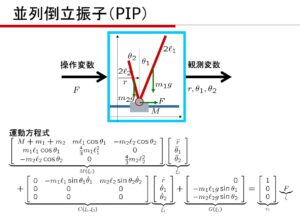
[6] 次の倒立振子の運動方程式を導き、状態空間表現を導け。