●
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{{= \left[\begin{array}{c} \int_0^1\phi(\xi)\frac{L^3}{EI} f_yd\xi \\ \int_0^1\psi(\xi)\frac{L^3}{EI} f_zd\xi \end{array}\right] }}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f3d6e1f672e4ba90ae9b31c279a8532e_l3.png)
●
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{ \frac{1}{||V_R(s,t)||} \left[\begin{array}{cc} V(s,t)-\dot{y}(s,t) & \dot{z}(s,t)\\ -\dot{z}(s,t)& V(s,t)-\dot{y}(s,t) \end{array}\right] \simeq \left[\begin{array}{cc} 1 & \frac{\dot{z}(s,t)}{V(s,t)}\\ -\frac{\dot{z}(s,t)}{V(s,t)} & 1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c69265b2242275612eaa865f4b447916_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{+ \left[\begin{array}{cc} 1 & \frac{\dot{z}(s,t)}{V(s,t)}\\ -\frac{\dot{z}(s,t)}{V(s,t)} & 1 \end{array}\right] \left[\begin{array}{c} f_{Dv}(s,t) \\ f_{L}(s,t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ab809214cf2b562459cd95b425f12869_l3.png)
![]()
●
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{ q_a(\tau)= \left[\begin{array}{c} q_{a1}(\tau) \\ \vdots\\ q_{aN}(\tau) \\ \end{array}\right],\ \phi(\xi)= \left[\begin{array}{c} \phi_1(\xi) \\ \vdots\\ \phi_N(\xi) \\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b30c392ff6c724f4b08c8d7b9827ec3b_l3.png)
![]()
![Rendered by QuickLaTeX.com \displaystyle{ p_b(\tau)= \left[\begin{array}{c} p_{b1}(\tau) \\ \vdots\\ p_{bN}(\tau) \\ \end{array}\right],\ \psi(\xi)= \left[\begin{array}{c} \psi_1(\xi) \\ \vdots\\ \psi_N(\xi) \\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2e4c15f6fa252b068e0f71555339a0a5_l3.png)
●
![]()
![]()
![]()
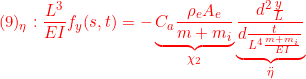

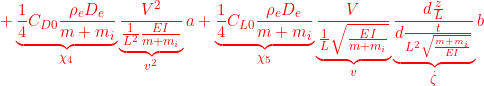
![]()
![]()
![]()
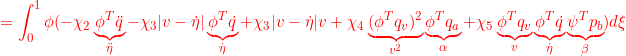
![]()
![]()
for ![]()
![]()
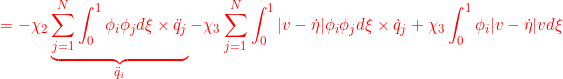
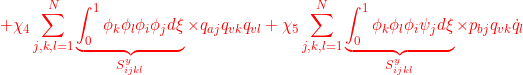
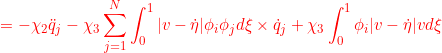
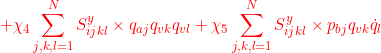
●
![]()
![]()
![]()
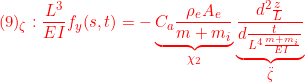
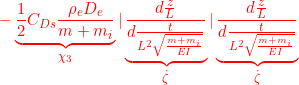
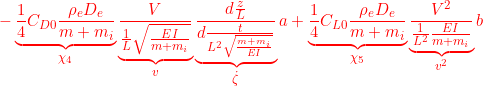
![]()
![]()
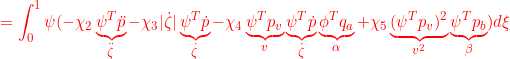
![]()
![]()
![]()
for ![]()
![]()
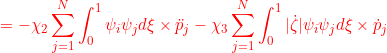
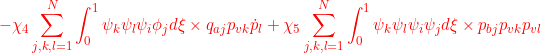
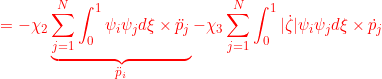
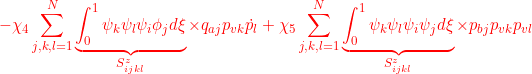
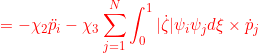
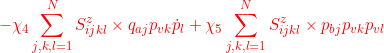
●
![]()
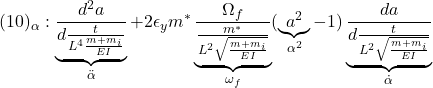
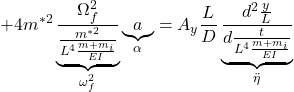
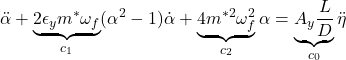
![]()
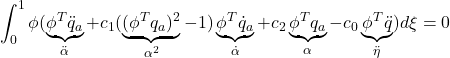
![]()
for ![]()
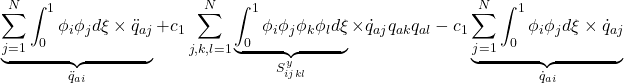
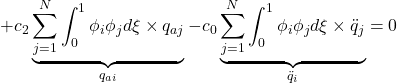
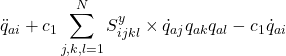
![]()
●
![]()
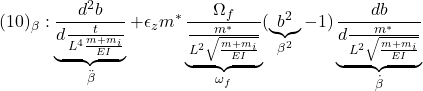
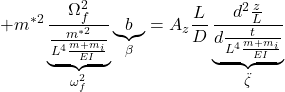
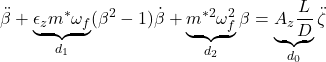
![]()
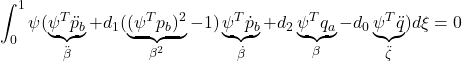
![]()
for ![]()
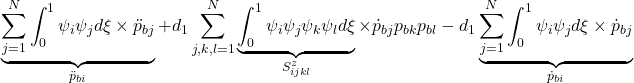
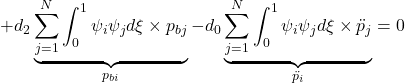
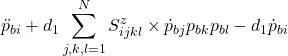
![]()
●
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{D_{qq}^a=[\chi_3\sum_{j=1}^N\int_0^1|v-\dot{\eta}|\phi_i\phi_jd\xi]_{i,j=1,\cdots,N}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-241b8cdd8b6e9aaf13c57a46ff008718_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{D_{qq}^b=[\chi_3\sum_{j=1}^N\int_0^1|\dot{\eta}|\psi_i\psi_jd\xi]_{i,j=1,\cdots,N} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e8f08ce28177cfbb21d1d507724ff197_l3.png)
![]()
![Rendered by QuickLaTeX.com \displaystyle{K_{q_aq_a}=[\chi_4 \displaystyle\sum_{l,k=1}^NS^y_{ijkl}q_{vk}q_{vl}]_{i,j=1,\cdots,N}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-80451502f16041f0bbac06fddc8c23c5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{K_{q_ap_b}=[-\chi_5 \displaystyle\sum_{l,k=1}^NS^y_{ijkl}q_{vk}\dot{q}_{l}]_{i,j=1,\cdots,N}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-98e603dd8e3c36879741d03b57b38686_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{K_{p_bq_a}=[\chi_4 \displaystyle\sum_{l,k=1}^NS^z_{ijkl}p_{vk}p_{vl}]_{i,j=1,\cdots,N}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4205b24c7abafe265267f45c15fd55e5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{K_{p_bp_b}=[\chi_5 \displaystyle\sum_{l,k=1}^NS^z_{ijkl}p_{vk}\dot{p}_{l}]_{i,j=1,\cdots,N}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-62eb249d80c1f756ba7c6165efddfe27_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{{\cal D}_{qq}^a=[c_1\displaystyle\sum_{l,k=1}^NS^y_{ijkl}q_{ak}q_{al}]_{i,j=1,\cdots,N}-c_1I_N}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-43ce9264c264e937f29b5242717b7b5c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{{\cal D}_{pp}^b=[d_1\displaystyle\sum_{l,k=1}^NS^z_{ijkl}p_{bk}p_{bl}]_{i,j=1,\cdots,N}-d_1I_N}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d57a70fb955339e4d56e602a8eb94956_l3.png)
●
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{{= \left[\begin{array}{c} \int_0^1\phi(\xi)\frac{L^3}{EI} f_yd\xi \\ \int_0^1\psi(\xi)\frac{L^3}{EI} f_zd\xi \end{array}\right] }}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f3d6e1f672e4ba90ae9b31c279a8532e_l3.png)
●
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{ \frac{1}{||V_R(s,t)||} \left[\begin{array}{cc} V(s,t)-\dot{y}(s,t) & \dot{z}(s,t)\\ -\dot{z}(s,t)& V(s,t)-\dot{y}(s,t) \end{array}\right] \simeq \left[\begin{array}{cc} 1 & \frac{\dot{z}(s,t)}{V(s,t)}\\ -\frac{\dot{z}(s,t)}{V(s,t)} & 1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c69265b2242275612eaa865f4b447916_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{+ \left[\begin{array}{cc} 1 & \frac{\dot{z}(s,t)}{V(s,t)}\\ -\frac{\dot{z}(s,t)}{V(s,t)} & 1 \end{array}\right] \left[\begin{array}{c} f_{Dv}(s,t) \\ f_{L}(s,t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ab809214cf2b562459cd95b425f12869_l3.png)
![]()
●
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{ q_a(\tau)= \left[\begin{array}{c} q_{a1}(\tau) \\ \vdots\\ q_{aN}(\tau) \\ \end{array}\right],\ \phi(\xi)= \left[\begin{array}{c} \phi_1(\xi) \\ \vdots\\ \phi_N(\xi) \\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b30c392ff6c724f4b08c8d7b9827ec3b_l3.png)
![]()
![Rendered by QuickLaTeX.com \displaystyle{ p_b(\tau)= \left[\begin{array}{c} p_{b1}(\tau) \\ \vdots\\ p_{bN}(\tau) \\ \end{array}\right],\ \psi(\xi)= \left[\begin{array}{c} \psi_1(\xi) \\ \vdots\\ \psi_N(\xi) \\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2e4c15f6fa252b068e0f71555339a0a5_l3.png)
●
![]()
![]()
![]()
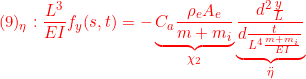

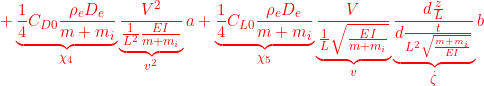
![]()
![]()
![]()
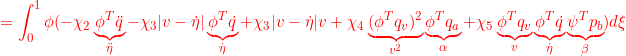
![]()
![]()
for ![]()
![]()
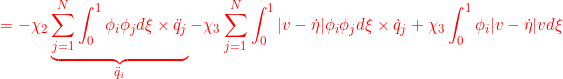
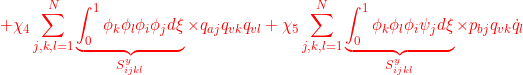
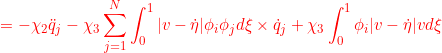
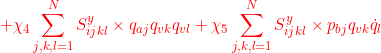
●
![]()
![]()
![]()
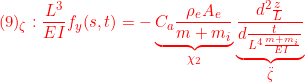
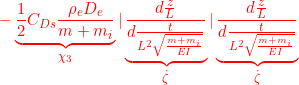
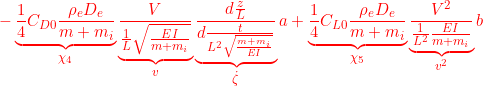
![]()
![]()
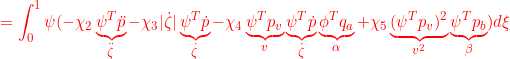
![]()
![]()
![]()
for ![]()
![]()
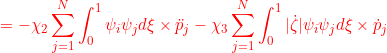
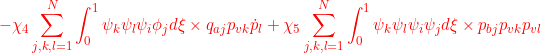
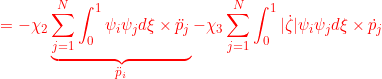
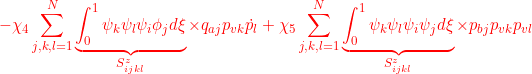
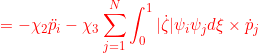
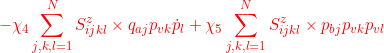
●
![]()
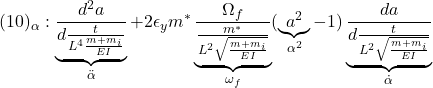
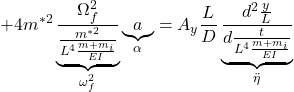
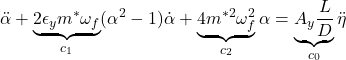
![]()
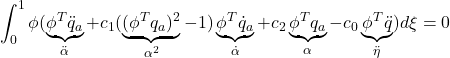
![]()
for ![]()
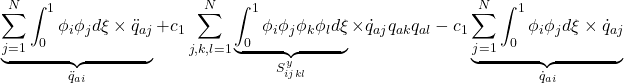
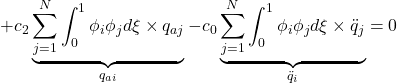
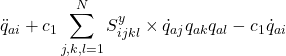
![]()
●
![]()

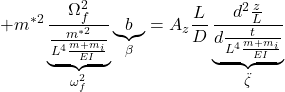
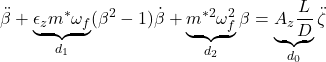
![]()
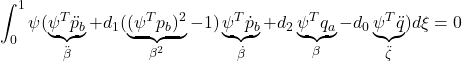
![]()
for ![]()
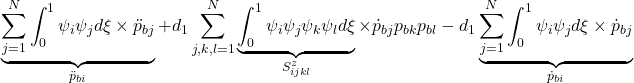
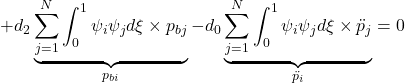
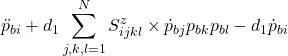
![]()
●
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{D_{qq}^a=[\chi_3\sum_{j=1}^N\int_0^1|v-\dot{\eta}|\phi_i\phi_jd\xi]_{i,j=1,\cdots,N}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-241b8cdd8b6e9aaf13c57a46ff008718_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{D_{qq}^b=[\chi_3\sum_{j=1}^N\int_0^1|\dot{\eta}|\psi_i\psi_jd\xi]_{i,j=1,\cdots,N} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e8f08ce28177cfbb21d1d507724ff197_l3.png)
![]()
![Rendered by QuickLaTeX.com \displaystyle{K_{q_aq_a}=[\chi_4 \displaystyle\sum_{l,k=1}^NS^y_{ijkl}q_{vk}q_{vl}]_{i,j=1,\cdots,N}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-80451502f16041f0bbac06fddc8c23c5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{K_{q_ap_b}=[-\chi_5 \displaystyle\sum_{l,k=1}^NS^y_{ijkl}q_{vk}\dot{q}_{l}]_{i,j=1,\cdots,N}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-98e603dd8e3c36879741d03b57b38686_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{K_{p_bq_a}=[\chi_4 \displaystyle\sum_{l,k=1}^NS^z_{ijkl}p_{vk}p_{vl}]_{i,j=1,\cdots,N}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4205b24c7abafe265267f45c15fd55e5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{K_{p_bp_b}=[\chi_5 \displaystyle\sum_{l,k=1}^NS^z_{ijkl}p_{vk}\dot{p}_{l}]_{i,j=1,\cdots,N}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-62eb249d80c1f756ba7c6165efddfe27_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{{\cal D}_{qq}^a=[c_1\displaystyle\sum_{l,k=1}^NS^y_{ijkl}q_{ak}q_{al}]_{i,j=1,\cdots,N}-c_1I_N}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-43ce9264c264e937f29b5242717b7b5c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{{\cal D}_{pp}^b=[d_1\displaystyle\sum_{l,k=1}^NS^z_{ijkl}p_{bk}p_{bl}]_{i,j=1,\cdots,N}-d_1I_N}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d57a70fb955339e4d56e602a8eb94956_l3.png)