Home Work 5.1
[C] 状態オブザーバは、当時学生だったルーエンバーガーが企業研修相当の機会で発明したものだと聞いたことがあるよ。実際、wikipediaには、次の記述があるね。
In his dissertation Luenberger introduced new methods for construction of state observers. The celebrated Luenberger observer is named after him.
[P] えー、すごいね。どうやって、見つけたのだろうか?やはり、推定誤差をネガティブ・フィードバックすれば、その誤差は小さくなるはずだと思ったのだろうね?
[M] 状態フィードバックによる安定化問題は、行列![]() と
と![]() を用いて、可安定性や可制御性として論じられるけど、状態オブザーバの構成問題は、行列
を用いて、可安定性や可制御性として論じられるけど、状態オブザーバの構成問題は、行列![]() と
と![]() を用いて、可検出性や可観測性として論じられているね。何せセンサの不足を補えるのだから、とてつもなく便利だよね。
を用いて、可検出性や可観測性として論じられているね。何せセンサの不足を補えるのだから、とてつもなく便利だよね。
Flipped Classroom 5.1
[1] (5.18)の左辺を計算すると
![]()
だから
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \begin{array}{ll} \det(\lambda I_n-A+HC)=\det\left[\begin{array}{cc}\lambda+h_1 & -1\\h_2 & \lambda+\frac{1}{T_m}\end{array}\right]\\ =(\lambda+h_1)(\lambda+\frac{1}{T_m})+h_2 =\lambda^2+(h_1+\frac{1}{T_m})\lambda+\frac{h_1}{T_m}+h_2 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-45bb6fc8e4ce84fa42476448fb19ae3e_l3.png)
これが右辺
![]()
に等しいので
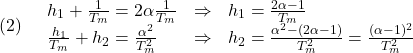
[2] ![]() の値によって状態推定の様子がどう違うを観察し、どちらの値が望ましいかをどう判定すればよいかを考えてみてください。
の値によって状態推定の様子がどう違うを観察し、どちらの値が望ましいかをどう判定すればよいかを考えてみてください。
(図5.3左図は縦軸の単位はradですが、Program 51ではdegに変換しています。配布するプログラムは、図5.3をそのまま出力します。)