|
私たちが制御したい対象が物である場合,その振る舞いは物理法則により記述される。一般に,動的な振る舞いを表す物理法則は微分方程式で表される。微分方程式というと尻込みする人もいるかもしれないが,最初は,ニュートンの運動第2法則 さて,制御を行うには対象の動的な振る舞い(状態変数の時間変化)を観測することが必要であり,そのためにセンサが用いられる。ここで,現実には,すべての状態変数にセンサを配置できるわけではなく,通常は状態変数の一部がセンサにより観測される。センサにより観測される変数と状態変数の間の関係式を,制御対象の「出力方程式」と呼ぶ。 本章では,動的な振る舞いが連立線形微分方程式で記述されるいくつかの制御対象に対して,状態方程式と出力方程式をペアにした「状態空間表現」を求める。これを図示した「ブロック線図」は,計算機シミュレーションを行う際にも有用である。 |
1.1 状態空間表現の導出例
1.1.1 ペースメーカ
|
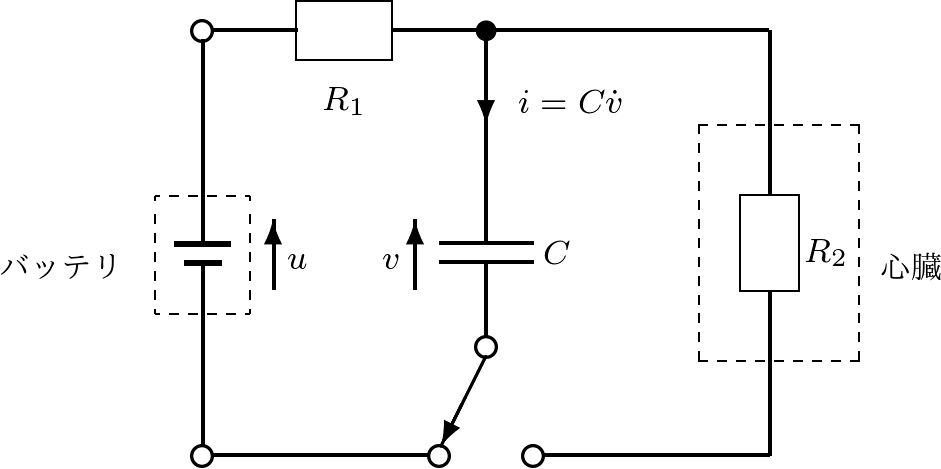
高齢化社会の到来に伴い,より優れた福祉・医療機器の開発が工学分野の大きなテーマの一つとなっている。図1.1に示すのは,心臓のペースメーカの簡単な原理図である。これは,まず左側の閉回路でコンデンサへの充電を行い,つぎにスイッチを切り替えてできる右側の閉回路で放電を行うという動作を周期的に繰り返すことにより,心臓のペースメーカの役割を果たそうとするものである。ここでは,状態方程式を導く最初の例として,このようなRC回路における充電と放電について考える。
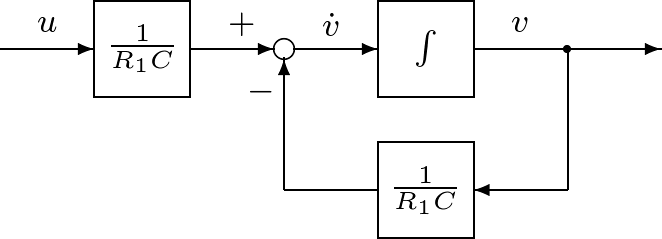
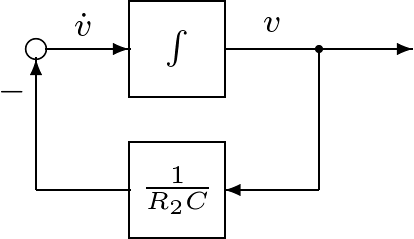
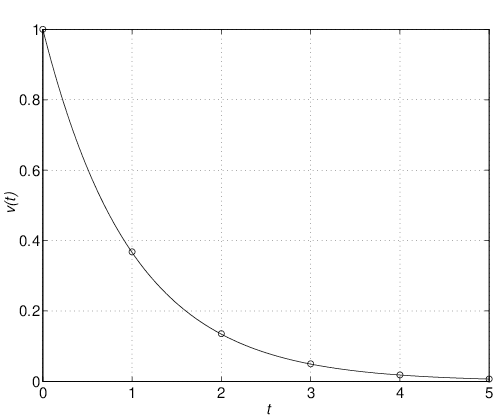
そのために,キルヒホッフの電圧則より,左側閉回路と右側閉回路の回路方程式を考えると,それぞれ (1) (2) となる。ここで, (3) 状態方程式(3)を図1.2のように図示し,これを状態方程式に基づくブロック線図と呼ぶ。この描き方のポイントは,式(3)の右辺を表すのに加え合わせ記号○を用いることと,また 同様に,式(2)から得られる状態方程式は (4) であり,これによるブロック線図は図1.3のように示される。 (5) と与えられることはよいであろう(式(4)に代入して確かめよ)。状態方程式(4)は入力変数をもたないが,状態変数の初期値によって,状態変数の時間的振る舞いが現れる。この意味で,1次系(4)は シミュレーション1.1 式(5)で表されるコンデンサ電圧 (6) によって近似計算しなさい。 |
*系はsystemの訳語。ここでは「××システム」を簡潔に「××系」と書く。
**本書では,時間応答のコンピュータによるシミュレーション(simulation)の欄を設けた。最終的には時間応答の数学的理解が大切であるが,まずは,なぜそのような時間的振る舞いが現れるのかを物理的イメージをもって考えながら,典型的な時間応答に親しみをもってほしい。なお,本書の数値計算については演習問題の【4】を参照のこと。
1.1.2 教室のドア
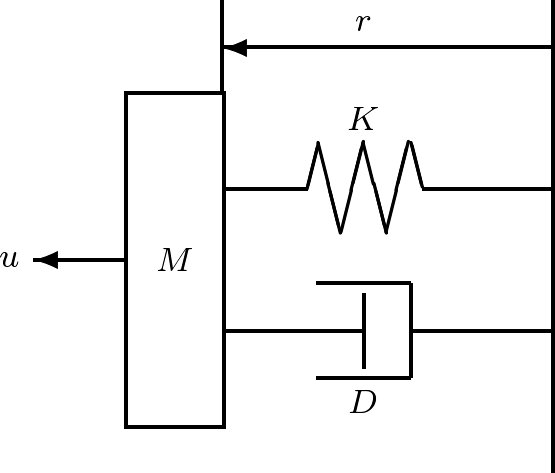
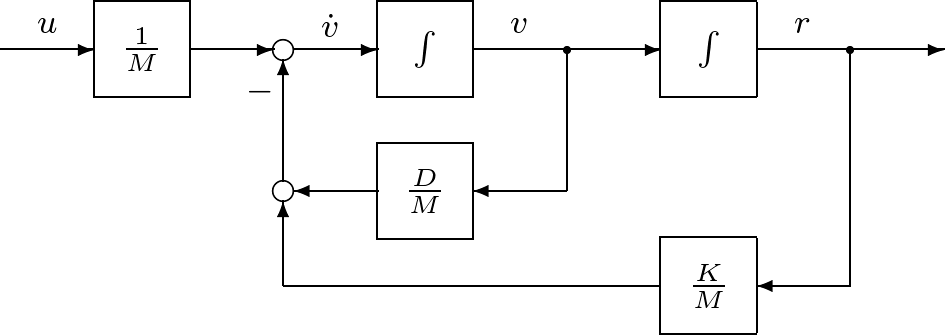
教室で物の動きを実感できるものに,図1.5に示すようなばねとダンパ 図1.5 緩衝装置をつけたドア このドアの運動は回転運動であるが,話しをわかりやすくするため,図1.6に示すような等価な直線運動として調べてみよう。その出発点は,ニュートンの運動第2法則 (7) である。ここで, (8) のように表すことができる。ここで,ダンパが第1項の力を,ばねが第2項の力を与える。 (9) を得る。 (10) (11) のような1階の連立線形微分方程式で表される。これらを行列表示すると (12) のような状態方程式を得る (13) を得るセンサはあるが,ドアの速度を計測するセンサはないものとする。このとき, (14) 以上から,ドアに対して,状態方程式(12)と出力方程式(14)からなる2次系(second-order system)としての状態空間表現を得た。 シミュレーション 式(12)において,
|
*ばねとダンパの特性値を調整するためのねじを回すことにより行われる。
**本書では,![]() のように書いて,△を○で定義・表記する(△は○に等しいとする)。
のように書いて,△を○で定義・表記する(△は○に等しいとする)。
1.1.3 直流モータ
|
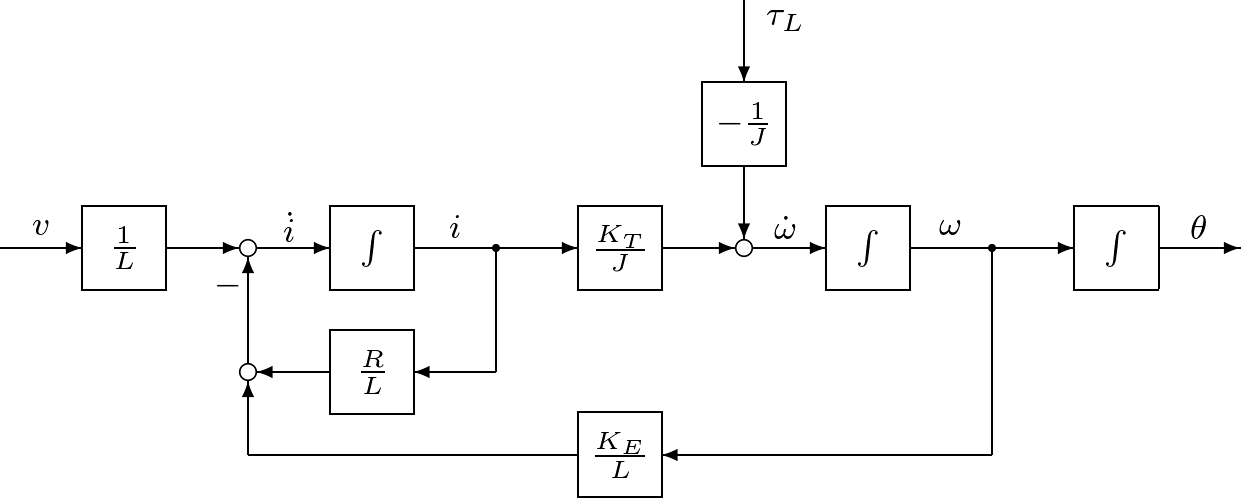
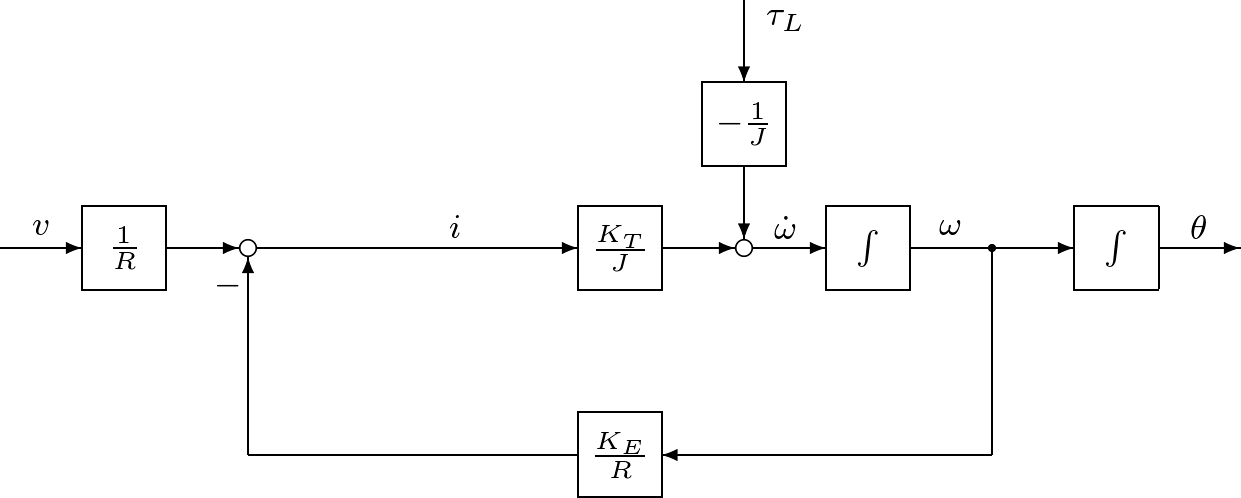
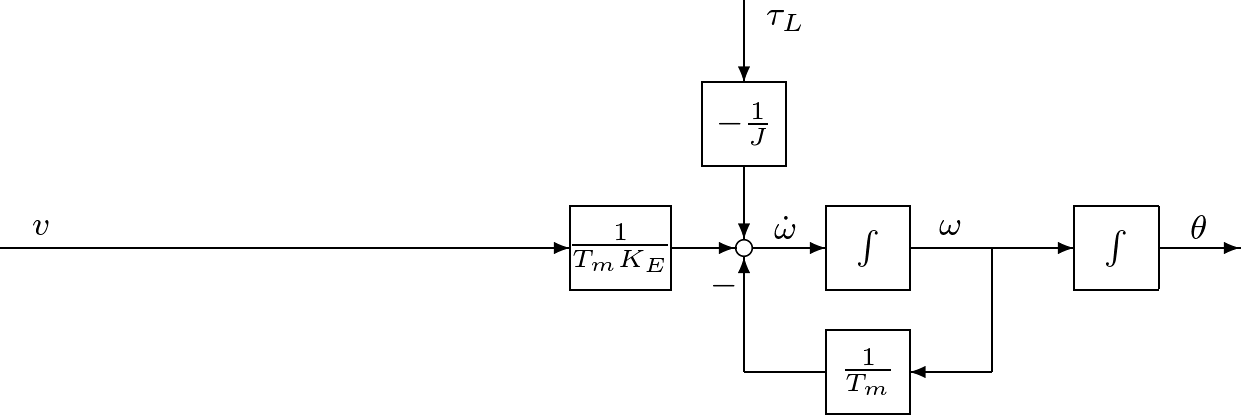
代表的なアクチュエータとしてモータがある。例えば図1.9に示すのは,ロボットアームを駆動する直流モータである。  図1.9 直流モータ このモデルは図1.10のように表される。 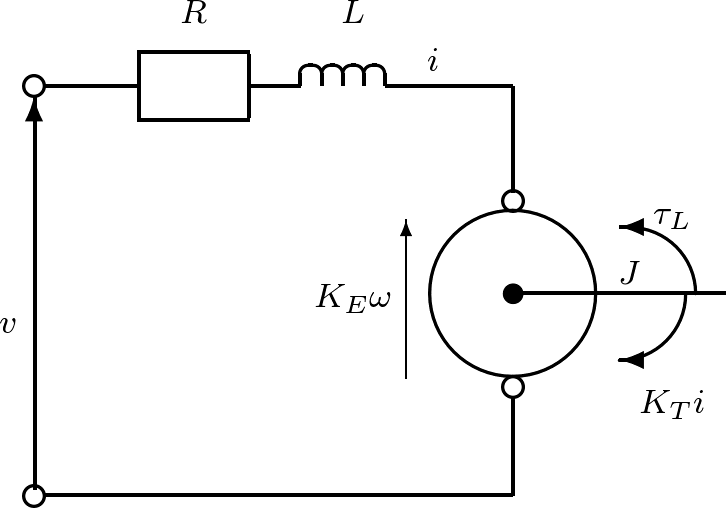 図1.10 直流モータのモデル このとき,つぎが成り立つ。 (15) (16) ここで,式(15)は機械系としての運動方程式であるが,電流による発生トルクの項 (17) (18) (19) のような状態方程式を得る。状態方程式(19)は二つの入力変数 (20) となる。このように,直流モータに対して,状態方程式(19)と出力方程式(20)からなる3次系(third-order system)としての状態空間表現を得た。つぎに一つのシミュレーション例を示す。 (21) で与えられ,上の例では (22) これから (23) (24) は直流モータの機械的時定数と呼ばれている。上の例で計算してみると (25) 式(19)と比較すると,状態空間表現の次数を1だけ減らしたことになる。 低次元化の過程を図1.12~図1.14に示しておく。 |
*式(18)は,式(19)のように物理パラメータどうしの演算を含まず,それらの変動の影響を考察するのに便利な形式であり,ディスクリプタ形式の状態方程式と呼ばれる。
**ここでは,2.1.3項で学ぶ時定数の知識を前提にしている。
1.2 状態空間表現へのモデリング
| 前節で述べた内容は,モデリング(modeling)という枠組でとらえられる。これは,何らかの対象に対して,目的に応じた科学的分析を通してそのモデルを得ようとするものである。私たちが扱う対象は,入力と出力をもつ動的システム 本書では,状態空間表現を次式のように書く。 (26) (27) ここで, |
*動的システムは,微分方程式・差分方程式のどちらで記述されるかによって連続時間系・離散時間系,重ね合わせの原理が成り立つか否かによって線形系・非線形系,常微分方程式か偏微分方程式かによって集中定数系・分布定数系,係数パラメータの時間依存性によって時変系・時不変系,入出力が確率過程であるか否かによって決定系・確率系などに分類される。
**非線形系の場合の取り扱いは7章で述べる。1~6章までは線形時不変系のみを扱う。
***他の数理モデルとして伝達関数表現がある。状態空間表現と伝達関数表現の間の相互関係については8章で述べる。
****他のアプローチとして,入力と出力の時系列データからモデリングを行うシステム同定がある。
1.3 状態空間表現の座標変換
| 状態空間表現を見やすくする一つの手段として,座標変換(coordinate transformation)があるので,これについて説明しよう。 いま, (28) (29) に対して,つぎの座標変換を行いたい。 (30) (31) に注意して (32) %すなわち (33) (34) となる。この結果を,参照しやすいようにつぎにまとめておく。 定理1.1 (35) (36) (37) 例題1.1 直流モータの状態方程式(25)において, (38) である。これに対して,座標変換 (39) を行うと,新しい状態方程式は (40) となることを示しなさい。 解答 座標変換後の (41) (42) のように得られる。 ここで,2次系の状態方程式が,二つの1次系の状態方程式 (43) に分離されており,入力から状態変数への影響の考察をしやすくなっていることに注意してほしい。 |
1.4 状態空間表現の直列結合
| 制御対象の状態空間表現を求める際に,図1.15に示すように,二つの部分システムの状態空間表現を求めておいて,これらを直列結合(serial connection)する場合がある。このときの結合システムの状態空間表現を求めることを考える。
まず,その結果を定理の形で示そう。 (44) (45) (46) (47) に対して, (48) (49) のように得られる。 証明 (50) (51) となる。第1式と (52) (53) に対して( (54) (55) を, 解答 定理1.2を用いて,直列結合の状態空間表現として (56) (57) が得られる 問1.4 例題1.2の直列結合の状態空間表現を,状態ベクトルが |
*ここで,![]() 行列の縦線と横線,
行列の縦線と横線,![]() 行列の横線は,状態ベクトルの要素
行列の横線は,状態ベクトルの要素![]() ,
,![]() のサイズに適合するように引かれている。
のサイズに適合するように引かれている。
演習問題
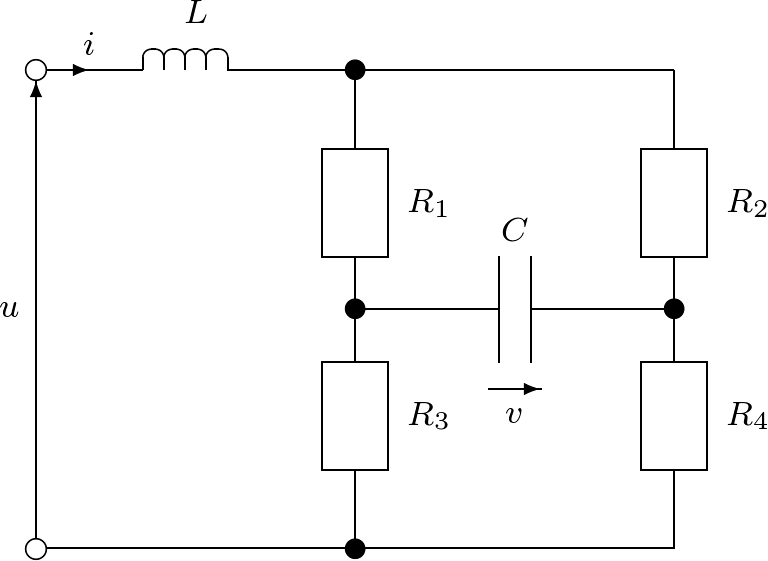
【1】 いろいろな計測装置の基礎となる電気回路の一つにブリッジ回路がある。 例えば,図1.16に示すブリッジ回路 (58) (59) で与えられる。いま,ブリッジ条件 (60) が成り立つとして,つぎの状態方程式を導出しなさい。 (61) この状態方程式に基づいて,平衡ブリッジ回路のブロック線図を描きなさい。
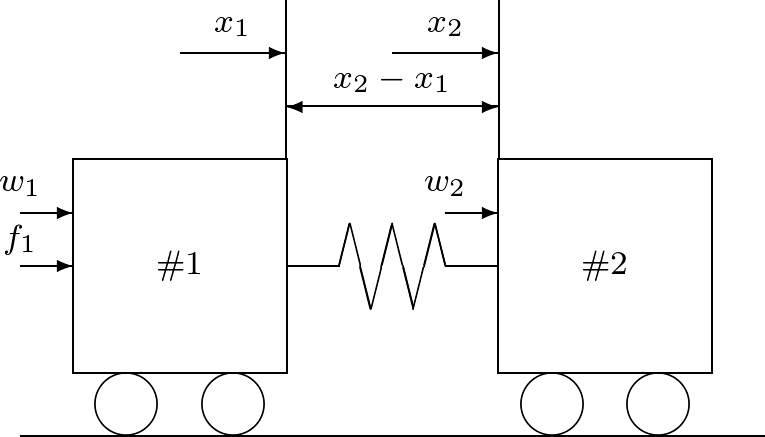
(62) (63) で与えられる。ここで, (64) この状態方程式に基づいて,連結台車のブロック線図を描きなさい。
MATLABとSIMULINKが手元にあれば,シミュレーション1.3と同一条件下で,直流モータの低次元化後の状態方程式25による角速度の応答を,低次元化前の状態方程式19によるものと比較しなさい。  図1.18 SIMULINKによる微分方程式のブロック表現 図1.18 SIMULINKによる微分方程式のブロック表現 |
*高橋・有本:回路網とシステム理論,コロナ社 (1974)のpp.65![]() 66から引用。
66から引用。
**B.Wie, D.2.Bernstein : Benchmark Problems for Robust Control Design, ACC Proc. pp.2047![]() 2048 (1992) から引用。
2048 (1992) から引用。
***The Student Edition of MATLAB-Version\,5 User’s Guide, Prentice Hall (1997)
****The Student Edition of SIMULINK-Version\,2 User’s Guide, Prentice Hall (1998)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{c} \dot{r}(t) \\ \dot{v}(t) \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\frac{K}{M} & -\frac{D}{M} \end{array}\right] }_A \underbrace{ \left[\begin{array}{c} r(t) \\ v(t) \end{array}\right] }_{x(t)}+ \underbrace{ \left[\begin{array}{c} 0 \\ \frac{1}{M} \end{array}\right] }_B u(t) \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1c7d500e812b8db8f7ef93fb748d863a_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{y_r(t)}_{y(t)}= \underbrace{ \left[\begin{array}{cc} c_r & 0 \end{array}\right] }_C \underbrace{ \left[\begin{array}{c} r(t) \\ v(t) \end{array}\right] }_{x(t)} \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ba917ead63a659449c7ce89833f94df6_l3.png)
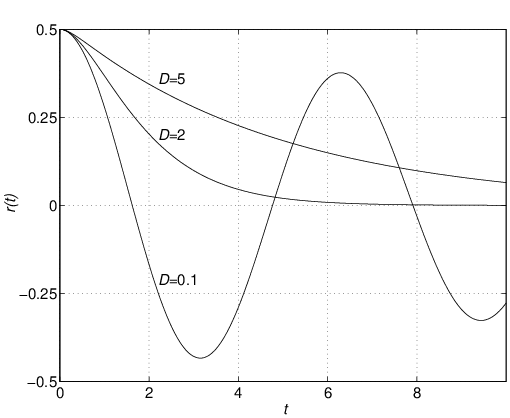
![Rendered by QuickLaTeX.com \begin{eqnarray*} %\begin{equation} %\renewcommand{\arraystretch}{1.3} %\begin{array}{rl} \underbrace{ \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & J & 0 \\ 0 & 0 & L \end{array}\right] }_{E} \left[\begin{array}{c} \dot{\theta}(t) \\ \dot{\omega}(t) \\ \dot{i}(t) \end{array}\right] & = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & K_T \\ 0 & -K_E & -R \end{array}\right] }_{A} \left[\begin{array}{c} \theta(t) \\ \omega(t) \\ i(t) \end{array}\right] \nonumber\\ & + \underbrace{ \left[\begin{array}{cc} 0 & 0 \\ 0 & -1 \\ 1 & 0 \end{array}\right] }_{B} \left[\begin{array}{cc} v(t) \\ \tau_L(t) \end{array}\right] %\end{array} %\end{equation} \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8c9f17ab2cf165ed53693c17a0d06a1b_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{c} \dot{\theta}(t) \\ \dot{\omega}(t) \\ \dot{i}(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & \frac{K_T}{J} \\ 0 & -\frac{K_E}{L} & -\frac{R}{L} \end{array}\right] }_{E^{-1}A} \underbrace{ \left[\begin{array}{c} \theta(t) \\ \omega(t) \\ i(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{cc} 0 & 0 \\ 0 & -\frac{1}{J} \\ \frac{1}{L} & 0 \end{array}\right] }_{E^{-1}B} \underbrace{ \left[\begin{array}{cc} v(t) \\ \tau_L(t) \end{array}\right] }_{u(t)} \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-26653bd3a6e2a14d2a2dd8ae426bf5f9_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{c} y_\theta(t) \\ y_\omega(t) \end{array}\right] }_{y(t)}= \underbrace{ \left[\begin{array}{ccc} c_\theta & 0 & 0 \\ 0 & c_\omega & 0 \end{array}\right] }_C \underbrace{ \left[\begin{array}{c} \theta(t) \\ \omega(t) \\ i(t) \end{array}\right] }_{x(t)} \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3d3a761f1082c0bb1c76cbac090b269d_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{c} \dot{\theta}(t) \\ \dot{\omega}(t) \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & -\frac{1}{T_m} \end{array}\right] }_A \underbrace{ \left[\begin{array}{c} \theta(t) \\ \omega(t) \end{array}\right] }_{x(t)}+ \underbrace{ \left[\begin{array}{cc} 0 & 0 \\ \frac{1}{T_mK_E} & -\frac{1}{J} \end{array}\right] }_B \underbrace{ \left[\begin{array}{c} v(t)\\ \tau_L(t) \end{array}\right] }_{u(t)} \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b6118b470740014f12ba99fab45c5044_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{c} \dot{\theta}(t)\\ \dot{\omega}(t) \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & -\frac{1}{T_m} \end{array}\right] }_A \underbrace{ \left[\begin{array}{c} \theta(t)\\ \omega(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ \frac{1}{T_mK_E} \end{array}\right] }_B \underbrace{ v(t) }_{u(t)} % \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-06edd7a3c72279d04bbf853ea6c6bdd5_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{c} x'_1(t) \\ x'_2(t) \end{array}\right] }_{x'(t)} = \underbrace{ \left[\begin{array}{cc} 1 & T_m \\ 0 & -T_m \end{array}\right] }_T \underbrace{ \left[\begin{array}{c} \theta(t) \\ \omega(t) \end{array}\right] }_{x(t)} % \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c6eae3ed06b9f97fd4eaffb60d82c161_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{c} \dot{x}'_1(t) \\ \dot{x}'_2(t) \end{array}\right] }_{\dot{x}'(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 0 \\ 0 & -\frac{1}{T_m} \end{array}\right] }_{A'} \underbrace{ \left[\begin{array}{c} x'_1(t) \\ x'_2(t) \end{array}\right] }_{x'(t)} + \underbrace{ \left[\begin{array}{c} \frac{1}{K_E} \\ -\frac{1}{K_E} \end{array}\right] }_{B'} \underbrace{ v(t) }_{u(t)} \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e26ebb2f15db7052666007c6f7713109_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{cc} 1 & T_m \\ 0 & -T_m \end{array}\right] \left[\begin{array}{cc} 0 & 1 \\ 0 & -\frac{1}{T_m} \end{array}\right] \left[\begin{array}{cc} 1 & 1 \\ 0 & -\frac{1}{T_m} \end{array}\right] }_{TAT^{-1}} = \underbrace{ \left[\begin{array}{cc} 0 & 0 \\ 0 & -\frac{1}{T_m} \end{array}\right] }_{A'} \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-063430e3eba82786ff27bab3362214fe_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{cc} 1 & T_m \\ 0 & -T_m \end{array}\right] \left[\begin{array}{cc} 0 \\ \frac{1}{T_mK_E} \end{array}\right] }_{TB} = \underbrace{ \left[\begin{array}{c} \frac{1}{K_E} \\ -\frac{1}{K_E} \end{array}\right] }_{B'} \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-782f939b9de9db6e02c2932b3e39543c_l3.png)

![Rendered by QuickLaTeX.com \begin{equation*} \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_a(t) \end{array}\right]= \left[\begin{array}{cc|c} 0 & 1 & 0\\ -\omega_n^2 & -2\zeta\omega_n & K\omega_n^2 \\\hline 0 & 0 & -\frac{1}{T_a} \end{array}\right] \left[\begin{array}{c} x(t) \\ x_a(t) \end{array}\right]+ \left[\begin{array}{cc} 0 \\ 0 \\\hline \frac{K_a}{T_a} \end{array}\right] u_a(t) \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-375c43a38aaae14e657cf77df359e493_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{c} \dot{i}(t) \\ \dot{v}(t) \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} -\frac{1}{L}(\frac{R_1R_2}{R_1+R_2}+\frac{R_3R_4}{R_3+R_4})\ \ 0 \\ 0\ \ -\frac{1}{C}(\frac{1}{R_1+R_2}+\frac{1}{R_3+R_4}) \end{array}\right] }_A \underbrace{ \left[\begin{array}{c} i(t) \\ v(t) \end{array}\right] }_{x(t)}+ \underbrace{ \left[\begin{array}{c} \frac{1}{L} \\ 0 \end{array}\right] }_B u(t) \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a8387d56c5b1e0a5d7e4371a7c5bf88f_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \begin{array}{rcl} \underbrace{ \left[\begin{array}{c} \dot{x_1}(t) \\ \dot{x_2}(t) \\ \dot{v_1}(t) \\ \dot{v_2}(t) \end{array}\right] }_{\dot{x}(t)} &=& \underbrace{ \left[\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ -\frac{k}{m_1} & \frac{k}{m_1} & 0 & 0 \\ \frac{k}{m_2} & -\frac{k}{m_2} & 0 & 0 \end{array}\right] }_A \underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \\ v_1(t) \\ v_2(t) \end{array}\right] }_{x(t)} \\ & & \hspace*{-1zw} + \underbrace{ \left[\begin{array}{ccc} 0 & 0 & 0 \\ 0 & 0 & 0 \\ \frac{1}{m_1} & 0 & \frac{1}{m_1} \\ 0 & \frac{1}{m_2} & 0 \end{array}\right] }_B \underbrace{ \left[\begin{array}{c} w_1(t)\\ w_2(t)\\ f_1(t) \end{array}\right] }_{u(t)} \end{array} \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-726aaf73212dd3c34a1e3daca7912d95_l3.png)