| 【本章のねらい】 ・ 振子を例に,MAXIMA ・ 振子の線形状態方程式を用いて,積分動作を加えた状態フィードバックのLQI設計を行い,これを非線形状態方程式に適用して,安定化シミュレーションを行う。 |
* http://ja.wikipedia.org/wiki/Maximaを参照。
7.1 非線形システムのモデリングの例
次の例題を考える。
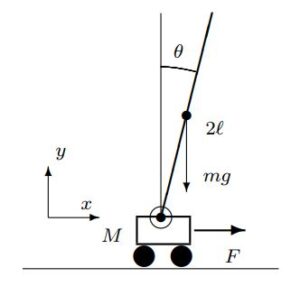
| 例題7.1 図7.1の振子を考える。MAXIMAを用いて,非線形運動方程式を計算し,これから非線形状態方程式を求めよ。さらに,平衡状態のまわりで線形化して,線形状態方程式を求めよ。
解答 運動エネルギー
に代入する。この計算をMAXIMAを用いて行うためには,コマンド |
| /*pen*/ dth:’diff(th(t),t); ddth:’diff(th(t),t,2); x:ell*sin(th(t)); y:ell*cos(th(t)); J:(1/3)*m*ell^2; T:(1/2)*m*(diff(x,t)^2+diff(y,t)^2)+(1/2)*J*dth^2; V:m*g*ell*cos(th(t)); L:T-V; LE:diff(diff(L,dth),t)-diff(L,th(t))=0,trigreduce; sol:solve(LE,ddth); f:matrix([dth],[rhs(sol[1])]); |
| を与えればよい
これより,非線形状態方程式
が求められる。平衡状態は
のように求められる。この平衡状態
を得る。この計算をMAXIMAを用いて行うためには,コマンド |
| A:matrix([diff(f[1,1],th(t)),diff(f[1,1],dth)], [diff(f[2,1],th(t)),diff(f[2,1],dth)]); |
| を与えればよい。すなわち,線形状態方程式は,次式のように求められる。
この線形状態方程式は,平衡状態近傍では,
と近似できるので,これを非線形運動方程式に代入し
を得て,これから直接求めることもできる。 |
| 演習7.1 例題7.1において, (1) (2) |
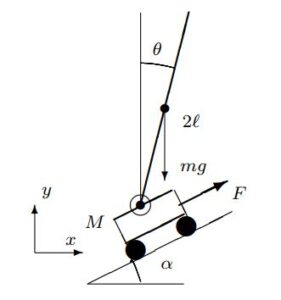
| 例題7.2 図7.2の台車によって駆動される振子を考える。MAXIMAを用いて,非線形運動方程式を計算し,これから非線形状態方程式を求めよ。さらに,平衡状態のまわりで線形化して,線形状態方程式を求めよ。
解答 台車の運動エネルギーは
に代入する。この計算をMAXIMAを用いて行うためには,コマンド |
| /*pend*/ dr:’diff(r(t),t); ddr:’diff(r(t),t,2); dth:’diff(th(t),t); ddth:’diff(th(t),t,2); T0:(1/2)*M*diff(r(t),t)^2; x1:r(t)+ell*sin(th(t)); y1:ell*cos(th(t)); J1:(1/3)*m*ell^2; T1:(1/2)*m*(diff(x1,t)^2+diff(y1,t)^2)+(1/2)*J1*dth^2; V1:m*g*y1; L:T0+T1-V1; LE1:diff(diff(L,dr),t)-diff(L,r(t))=F,trigreduce,ratsimp; LE2:diff(diff(L,dth),t)-diff(L,th(t))=0,trigreduce,ratsimp; sol:solve([LE1,LE2],[ddr,ddth]); |
| を与えればよい。この結果から,非線形運動方程式
が得られる。これより,非線形状態方程式
が求められる。平衡状態は,
のように求められる。この平衡状態近傍で,
を得る。この計算をMAXIMAを用いて行うためには,コマンド |
| f:matrix([dr],[dth],[rhs(sol[1][1])],[rhs(sol[1][2])]); a31:diff(f[3,1],r(t)); a32:diff(f[3,1],th(t)); a33:diff(f[3,1],dr); a34:diff(f[3,1],dth); a41:diff(f[4,1],r(t)); a42:diff(f[4,1],th(t)); a43:diff(f[4,1],dr); a44:diff(f[4,1],dth); b3:diff(f[3,1],F); b4:diff(f[4,1],F); A:matrix([0,0,1,0],[0,0,0,1],[a31,a32,a33,a34], [a41,a42,a43,a44]); B:matrix([0],[0],[b3],[b4]); A1:A,th(t)=0,F=0,trigreduce,ratsimp; B1:B,th(t)=0,F=0,trigreduce,ratsimp; A2:A,th(t)=%pi,F=0,trigreduce,ratsimp; B2:B,th(t)=%pi,F=0,trigreduce,ratsimp; |
| を与えればよい。この結果から,
となる。また,
|
| 演習7.2 例題7.2の振子を軸支した台車を,図7.3のように傾斜角
|
| 例題7.3 例題7.2の台車によって駆動される振子について,そこで求めた状態方程式に基づいて,MAXIMAを用いて,漸近安定性と可制御性について調べよ。
解答 まず,安定性を調べるために, |
| lambda:eigenvalues(A1); |
| その結果, つぎに,可制御性を, |
| rank(addcol(A1-lambda[1][1]*ident(4),B1)); rank(addcol(A1-lambda[1][2]*ident(4),B1)); rank(addcol(A1-lambda[2][1]*ident(4),B1)); rank(addcol(A1-lambda[2][2]*ident(4),B1)); |
| % For[i = 1, i % W=MapThread[Append,{A-lambda[[i]] IdentityMatrix[4],B}]; % Print[MatrixRank[W]]; i++] のコマンドを与えればよい。その結果,階数はすべて4と計算され,可制御性が成り立つ。 |
| 演習7.3 例題7.3を, |
7.2 非線形系に対する線形制御の適用
つぎの例題を考える。
| 例題7.4 例題7.2の台車によって駆動される倒立振子について,台車の位置 解答 まず,出力方程式として
を得る。また,台車の位置
のように表される。このとき,正方行列
は正則である。したがって,次式が定まる。
つぎに,偏差系
に対する評価関数を,たとえば
のように設定する。ここで, 制御目的を達成する積分動作を加えた状態フィードバック
は,上の評価関数を最小にするように,状態フィードバック
を求め,次式から
以上の計算を,MATLABで行うためには |
| %pend.m global M m ell g th0 M=1; m=0.1; ell=0.25; g=9.8; th0=3/180*pi; E=[M+m m*ell;m*ell (4/3)*m*ell^2]; A21=-E\[0 0;0 -m*ell*g]; A=[zeros(2) eye(2);A21 zeros(2)] B2=E\[1;0]; B=[zeros(2,1);B2] CM=[1 0 0 0;0 1 0 0]; CS=[1 0]; C=CS*CM; AE=[A B;zeros(1,5)]; BE=[zeros(4,1); 1]; CE=eye(5); Tcart=0.1; Kr=0.5; Tpend=(1/4)*(2*pi*sqrt(4/3*ell/g)); Kth=5/180*pi; Tamp=0.1; Kamp=5; q1=1/Kr; q2=1/Kth; q3=Tcart/Kr; q4=Tpend/Kth; q5=1/Kamp; QE=diag([q1 q2 q3 q4 q5].^2); RE=(Tamp/Kamp)^2; [FE,pAE]=opt(AE,BE,CE,QE,RE) FE=FE/[A B;C 0]; F=FE(:,1:4); FI=FE(:,5); ACL=[A-B*F -B*FI;C 0]; BCL=[zeros(4,1);-0.5]; CCL=[CM zeros(2,1);-F -FI]; DCL=[zeros(2,1);0]; sys=ss(ACL,BCL,CCL,DCL); step(sys) |
| を与えればよい。 |
もちろん,これらは重み係数の初期値であり,実際には調整を伴うことはいうまでもない。
| 演習7.4 演習7.3のように,振子を軸支した台車を傾斜角 |
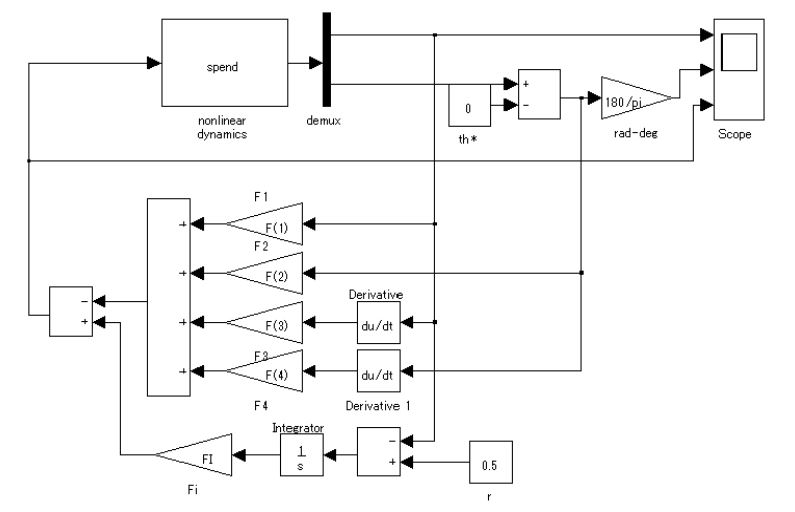
| 例題7.5 例題7.4で設計した積分動作を加えた状態フィードバックを,非線形ダイナミクスを表す非線形状態方程式と結合して,閉ループ系の時間応答をシミュレーションせよ。
解答 まず,非線形状態方程式を,つぎのS-functionで記述する。 |
| %spend.m function [sys,x0]=spend(t,state,input,flag) global M m ell g th0 if abs(flag)==1 u =input(1); r =state(1); th =state(2); dr =state(3); dth=state(4); Mp=[M+m m*ell*cos(th); m*ell*cos(th) (4/3)*m*ell^2]; Cp=[0 -m*ell*dth*sin(th);0 0]; Gp=[0; -m*ell*g*sin(th)]; sys=[dr;dth;Mp\(-Cp*[dr;dth]-Gp+[u;0])]; elseif flag==3, sys=state(1:2); elseif flag==0 sys=[4;0;2;1;0;0]; x0=[0;th0;0;0]; else sys=[]; end |
| つぎに,Simulink上に
のように,このS-functionブロックと例題??で設計した積分動作を加えた状態フィードバックを接続して,シミュレーションを行う。 |
| 演習7.5 演習7.4で設計した積分動作を加えた状態フィードバックを,非線形ダイナミクスを表す非線形状態方程式と結合して,閉ループ系の時間応答をシミュレーションせよ。 |
演習問題の解答
| 【演習7.1】Simulinkを用いて,次図のブロック線図を作成する。
上半分が非線形運動方程式 |
| 【演習7.2】非線形運動方程式を求める計算をMAXIMAを用いて行うためには |
| /*pend2*/ dr:’diff(r(t),t); ddr:’diff(r(t),t,2); dth:’diff(th(t),t); ddth:’diff(th(t),t,2); x0:r(t)*cos(alpha); y0:r(t)*sin(alpha); T0:(1/2)*M*(diff(x0,t)^2+diff(y0,t)^2); V0:M*g*y0; x1:x0+ell*sin(th(t)); y1:y0+ell*cos(th(t)); J1:(1/3)*m*ell^2; T1:(1/2)*m*(diff(x1,t)^2+diff(y1,t)^2)+(1/2)*J1*dth^2; V1:m*g*y1; L:T0+T1-V0-V1; LE1:diff(diff(L,dr),t)-diff(L,r(t))=F,trigreduce,ratsimp; LE2:diff(diff(L,dth),t)-diff(L,th(t))=0,trigreduce,ratsimp; sol:solve([LE1,LE2],[ddr,ddth]); |
のコマンドを与えればよい。この結果から,非線形運動方程式![Rendered by QuickLaTeX.com \underbrace{ \left[\begin{array}{cc} M+m & m\ell\cos(\theta+\alpha) \\ m\ell\cos(\theta+\alpha) & \frac{4}{3}m\ell^2 \end{array}\right] }_{M(\theta)} \underbrace{ \left[\begin{array}{c} \ddot{r}\\ \ddot{\theta} \end{array}\right] }_{\ddot{\xi}_1} + \underbrace{ \left[\begin{array}{cc} 0 & -m\ell\dot{\theta}\sin(\theta+\alpha) \\ 0 & 0 \end{array}\right] }_{C(\theta)} \underbrace{ \left[\begin{array}{c} \dot{r}\\ \dot{\theta} \end{array}\right] }_{\dot{\xi}_1}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b6922d7711b2f0f96db4501e90739345_l3.png) ![Rendered by QuickLaTeX.com + \underbrace{ \left[\begin{array}{c} 0 \\ -m\ell g\sin\theta \end{array}\right] }_{G(\theta)} = \underbrace{ \left[\begin{array}{c} F-(M+m)g\sin\alpha\\ 0 \end{array}\right] }_{\zeta}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d1078acd06df1fb0cd7feb9d9fffcb18_l3.png) が得られる。これより,平衡状態は ![Rendered by QuickLaTeX.com \xi^* =\left[\begin{array}{c} 0 \\ \theta^* \\ 0 \\ 0 \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-494e62c3407794d38dafa6f7008aea42_l3.png) ( (のように求まる。 ![Rendered by QuickLaTeX.com \underbrace{ \frac{d}{dt} \left[\begin{array}{c} r \\ \theta \\ \dot{r} \\ \dot{\theta} \end{array}\right] }_{\dot x} = \underbrace{ \left[\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & -\frac{6mg\cos\alpha}{8M+(5-3\cos2\alpha)m} & 0 & 0 \\ 0 & \frac{6(M+m)g}{(8M+(5-3\cos2\alpha)m)\ell} & 0 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} r \\ \theta \\ \dot{r} \\ \dot{\theta} \end{array}\right] }_{x}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-92877f60035f32a0435dbc3738e4be0d_l3.png) \\ \\![Rendered by QuickLaTeX.com + \underbrace{ \left[\begin{array}{cccc} 0 \\ 0 \\ \frac{8}{8M+(5-3\cos2\alpha)m} \\ -\frac{6\cos\alpha}{(8M+(5-3\cos2\alpha)m)\ell} \\ \end{array}\right] }_{B} \underbrace{ (F-(M+m)g\sin\alpha) }_{u}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-62f774fb9a1f073d682e3fbb5ca13050_l3.png) |
| 【演習7.3】 |
|
%pend.m M=1; m=0.1; ell=0.25; g=9.8; E=[M+m m*ell;m*ell (4/3)*m*ell^2]; A21=-E\[0 0;0 -m*ell*g]; A=[zeros(2) eye(2);A21 zeros] B2=E\[1;0]; B=[zeros(2,1);B2] r=eig(A) tol=1e-6; for i=1:4, k=rank([B A-r(i)*eye(4)],tol), end |
| 【演習7.4】次を実行し,あとは例題7.4と同様に行えばよい。 |
| %pend2.m M=1; m=0.1; ell=0.25; g=9.8; alpha=5/180*pi; a32=-(3*m*g*cos(alpha))/(7*M+(11-3*cos(2*alpha))/2*m); a42=(3*(M+m)*g)/(7*M+(11-3*cos(2*alpha))/2*m)/ell; b3=7/(7*M+(11-3*cos(2*alpha))/2*m); b4=-3/(7*M+(11-3*cos(2*alpha))/2*m)/ell; A21=[0 a32;0 a42]; A=[zeros(2) eye(2);A21 zeros(2)] B2=[b3;b4]; B=[zeros(2,1);B2] |
| 【演習7.5】まず,非線形ダイナミクスを,つぎのS-functionで記述する。 |
| %spend2.m function [sys,x0]=spend2(t,state,input,flag) M=1; m=0.1; ell=0.25; g=9.8; th0=0; alpha=5/180*pi; if abs(flag)==1 u=input(1); r=state(1); th=state(2); dr=state(3); dth=state(4); Mp=[M+m m*ell*cos(th+alpha); m*ell*cos(th+alpha) (7/3)*m*ell^2]; Cp=[0 -m*ell*dth*sin(th+alpha);0 0]; Gp=[0; -m*ell*g*sin(th)]; sys=[dr;dth;Mp elseif flag==3 sys=state(1:2); elseif flag==0 sys=[4;0;2;1;0;0]; x0=[0;th0;0;0]; else sys=[]; end |
| Simulink上に,このS-functionブロックと,演習7.4で設計した積分動作を加えた状態フィードバックを記述して,シミュレーションを行う。詳細は割愛する。 |

![Rendered by QuickLaTeX.com \underbrace{ \left[\begin{array}{c} \dot{\theta}\\ \ddot{\theta} \end{array}\right] }_{\dot \xi} = \underbrace{ \left[\begin{array}{c} \dot{\theta}\\ \frac{3g}{4\ell}\sin\theta \end{array}\right] }_{f(\xi)}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2a78ef4b7d2b88e22f838f474b01b538_l3.png)
![Rendered by QuickLaTeX.com \underbrace{ \left[\begin{array}{c} f_1(\xi)\\ f_2(\xi) \end{array}\right] }_{f(\xi)} \simeq \underbrace{\left. \left[\begin{array}{cc} 0 & 1 \\ \frac{\partial f_2}{\partial\theta} & \frac{\partial f_2}{\partial\dot{\theta}} \end{array}\right]\right|_{{\theta=\theta^*}\atop{\dot{\theta}=0\ }} }_{A} \underbrace{ \left[\begin{array}{c} \theta-\theta^*\\ \dot{\theta} \end{array}\right] }_{x=\xi-\xi^*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-40619fb8aefc66df2a9f1690d2b51bed_l3.png)
![Rendered by QuickLaTeX.com \underbrace{ \frac{d}{dt} \left[\begin{array}{c} \theta-\theta^*\\ \dot{\theta} \end{array}\right] }_{\dot x} = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ \frac{3g}{4\ell}\cos\theta^* & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \theta-\theta^*\\ \dot{\theta} \end{array}\right] }_{x}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e20bbd8807203333d0f192d00bf9a3ef_l3.png)
![Rendered by QuickLaTeX.com \underbrace{ \left[\begin{array}{cc} M+m & m\ell\cos\theta \\ m\ell\cos\theta & \frac{4}{3}m\ell^2 \end{array}\right] }_{M(\theta)} \underbrace{ \left[\begin{array}{c} \ddot{r}\\ \ddot{\theta} \end{array}\right] }_{\ddot{\xi}_1} + \underbrace{ \left[\begin{array}{cc} 0 & -m\ell\dot{\theta}\sin\theta \\ 0 & 0 \end{array}\right] }_{C(\theta)} \underbrace{ \left[\begin{array}{c} \dot{r}\\ \dot{\theta} \end{array}\right] }_{\dot{\xi}_1}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c3ca9545327d374f12a7a3b48f8bd6d8_l3.png) \\
\\![Rendered by QuickLaTeX.com + \underbrace{ \left[\begin{array}{c} 0 \\ -m\ell g\sin\theta \end{array}\right] }_{G(\theta)} = \underbrace{ \left[\begin{array}{c} F\\ 0 \end{array}\right] }_{\zeta}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dff2f69ef0d1c2deefbae29b72fb58f3_l3.png)
![Rendered by QuickLaTeX.com \underbrace{ \left[\begin{array}{c} \dot{\xi}_1\\ \ddot{\xi}_1 \end{array}\right] }_{\dot \xi} = \underbrace{ \left[\begin{array}{c} \dot{\xi}_1\\ -M(\theta)^{-1}(\zeta-C(\theta)\dot{\xi}_1-G(\theta)) \end{array}\right] }_{f(\xi,\zeta)}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f427ac559f4a9bf3589bed5bf3b87104_l3.png)
![Rendered by QuickLaTeX.com \underbrace{ \left[\begin{array}{c} \dot{r}\\ \dot{\theta}\\ f_3(r,\theta,\dot{r},\dot{\theta})\\ f_4(r,\theta,\dot{r},\dot{\theta})\\ \end{array}\right] }_{f(\xi,\zeta)} \simeq \underbrace{\left. \left[\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \frac{\partial f_3}{\partial r} & \frac{\partial f_3}{\partial\theta} & \frac{\partial f_3}{\partial\dot{r}} & \frac{\partial f_3}{\partial\dot{\theta}} \\ \frac{\partial f_4}{\partial r} & \frac{\partial f_4}{\partial\theta} & \frac{\partial f_4}{\partial\dot{r}} & \frac{\partial f_4}{\partial\dot{\theta}} \end{array}\right] \right|_{{{{{r=0}\atop{\theta=\theta^*}}\atop{\dot{r}=0}}\atop{\dot{\theta}=0}}\atop{F^*=0}} }_{A} \underbrace{ \left[\begin{array}{c} r \\ \theta-\theta^* \\ \dot{r} \\ \dot{\theta} \end{array}\right] }_{x=\xi-\xi^*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-28af87870eb0ee575637ef26ea72751e_l3.png)
![Rendered by QuickLaTeX.com + \underbrace{\left. \left[\begin{array}{c} 0 \\ 0 \\ \frac{\partial f_3}{\partial F} \\ \frac{\partial f_4}{\partial F} \end{array}\right] \right|_{{{{{r=0}\atop{\theta=\theta^*}}\atop{\dot{r}=0}}\atop{\dot{\theta}=0}}\atop{F^*=0}} }_{B} \underbrace{ F }_{u}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c6c66c6fa11494395e52f2856f245118_l3.png)
![Rendered by QuickLaTeX.com \underbrace{ \frac{d}{dt} \left[\begin{array}{c} r \\ \theta \\ \dot{r} \\ \dot{\theta} \end{array}\right] }_{\dot x} = \underbrace{ \left[\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & -\frac{3mg}{4M+m} & 0 & 0 \\ 0 & \frac{3(M+m)g}{(4M+m)\ell} & 0 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} r \\ \theta \\ \dot{r} \\ \dot{\theta} \end{array}\right] }_{x} + \underbrace{ \left[\begin{array}{cccc} 0 \\ 0 \\ \frac{4}{4M+m} \\ -\frac{3}{(4M+m)\ell} \\ \end{array}\right] }_{B} \underbrace{ F }_{u}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ba8959ac6db881665315c9c4984ce39d_l3.png)
![Rendered by QuickLaTeX.com \underbrace{ \frac{d}{dt} \left[\begin{array}{c} r \\ \theta-\pi \\ \dot{r} \\ \dot{\theta} \end{array}\right] }_{\dot x} = \underbrace{ \left[\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & -\frac{3mg}{4M+m} & 0 & 0 \\ 0 & -\frac{3(M+m)g}{(4M+m)\ell} & 0 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} r \\ \theta-\pi \\ \dot{r} \\ \dot{\theta} \end{array}\right] }_{x} + \underbrace{ \left[\begin{array}{cccc} 0 \\ 0 \\ \frac{4}{4M+m} \\ \frac{3}{(4M+m)\ell} \\ \end{array}\right] }_{B} \underbrace{ F }_{u}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-55c9a98a3b25a90144337fc86d41c888_l3.png) \\
\\
![Rendered by QuickLaTeX.com \underbrace{ \left[\begin{array}{c} r \\ \theta \end{array}\right] }_{y_M} = \underbrace{ \left[\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{array}\right] }_{C_M} \underbrace{ \left[\begin{array}{c} r \\ \theta \\ \dot{r} \\ \dot{\theta} \end{array}\right] }_{x}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6baa8fc6b84d2586dd49b58ef433c5fe_l3.png)
![Rendered by QuickLaTeX.com \underbrace{ r }_{z} = \underbrace{ \left[\begin{array}{cccc} 1 & 0 \end{array}\right] }_{C_S} \underbrace{ \left[\begin{array}{c} r \\ \theta \end{array}\right] }_{y_M} = \underbrace{ \left[\begin{array}{cccc} 1 & 0 & 0 & 0 \end{array}\right] }_{C=C_SC_M} \underbrace{ \left[\begin{array}{c} r \\ \theta \\ \dot{r} \\ \dot{\theta} \end{array}\right] }_{x}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-05c56d73b83531ae91ffbf08372ccd6a_l3.png)
![Rendered by QuickLaTeX.com S=\left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] = \left[\begin{array}{cccc:c} 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & -\frac{3mg}{4M+m} & 0 & 0 & \frac{3}{4M+m}\\ 0 & \frac{3(M+m)g}{(4M+m)\ell} & 0 & 0 & -\frac{3}{(4M+m)\ell} \\ \hdashline 1 & 0 & 0 & 0 & 0 \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-23f8500a01f8e1021ee1d64e187eff87_l3.png)
![Rendered by QuickLaTeX.com \left[\begin{array}{c} x_\infty \\ u_\infty \end{array}\right] = \left[\begin{array}{c} r_\infty \\ \theta_\infty \\ \dot{r}_\infty \\ \dot{\theta}_\infty \\\hdashline u_\infty \end{array}\right] =S^{-1} \left[\begin{array}{c} 0 \\ 0 \\ 0 \\ 0 \\\hdashline r^* \end{array}\right] = \left[\begin{array}{c} r^* \\ 0 \\ 0 \\ 0 \\\hdashline 0 \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-964e005b0fd9999c976a917896e43759_l3.png)
![Rendered by QuickLaTeX.com \frac{d}{dt} \underbrace{ \left[\begin{array}{c} x-x_\infty \\ u-u_\infty \end{array}\right] }_{x_{E3}} = \underbrace{ \left[\begin{array}{cccc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} \underbrace{ \left[\begin{array}{c} x-x_\infty \\ u-u_\infty \end{array}\right] }_{x_{E3}} + \underbrace{ \left[\begin{array}{cccc} 0 \\ 1 \\ \end{array}\right] }_{B_{E3}} \dot{u}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f23734294bd218f2bca348f310c80f7b_l3.png)