| これまで,安定性の定義,安定化の可能性とその方策を学んできた。その結果,私たちは,閉ループ系の零入力応答を適切に安定化する,すなわち,ある初期状態から出発して速やかに零状態(平衡状態)にもっていくことはできる。この零入力応答は,適当な強さのインパルス入力に対する零状態応答に等しいことを思い出してほしい。
例えば,一定速度で回転しているモータを考え,これに瞬間的な負荷がかかって,その速度が乱されたとする。このときは,状態フィードバックによってもとの速度に復帰させることができる。しかし,モータで何か対象物を回転させるときは,モータ軸への持続的な負荷が生じ,極端な場合はモータは回転することさえできないであろう。同様に,飛行機,船舶,車などのビークルに強い向い風が吹けば定速を維持することは困難となるであろう。 また,モータやビークルでは,速度の設定値を変えることが制御の大切な役割なのに,そのための手段はまったく学んでいない。 したがって,これまでの知識だけでは多くの現実問題を解くことはできない。実際の問題では,必ずといっていいほど,さまざまな「定値外乱」の影響を受ける状況のもとで,「設定値」の保持や,ときには変更を要求されるからである。このような問題を解決するためには,これまでの制御方式に加えて,まず「積分動作」の導入による構造的な改良が必要となる。本章では,定値外乱の影響の除去や,設定値の変更に対応できるように,積分動作を入れて安定化を行う方策について学ぶ。その安定化にLQ制御を適用するとき,その制御方式を簡潔に表すために「LQI制御」と呼ぶ。 |
6.1 1次系における定値外乱の影響を抑制する
6.1.1 定値外乱の影響
| 1章で述べた直流モータの状態方程式(1.11)すなわち
を思い出そう。これは,二つの入力変数 以下では,この状況を一般化した次式で表される1次系を考える。
ここで,
いま,1次系(2)に対して,状態フィードバック
を行うと,閉ループ系
を得る。ここで,
となる。第2項は
と計算できるので,
すなわち,定値外乱が加わると
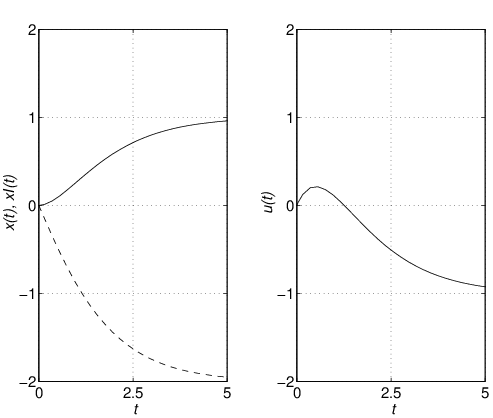
とはならない。このことをシミュレーション例で確認しよう。 シミュレーション 6.1
このような定値外乱の影響を取り除くために,式(3)の代わりに
のような方策を用いる。このときの閉ループ系
の時間応答は
となる。これより,外乱を打ち消すように
と選べば,式(8)を達成できる。しかしながら, |
図6.2の下に次の問を設定していましたが,紙幅の関係で省略しました。
図6.2で,![]() であることを確かめなさい。
であることを確かめなさい。
6.1.2 積分動作を加える
| この方法の基礎となるアイデアは
を達成できれば そこで,式(13)を満足する
を達成することができないか検討しよう。 まず,式(2)と,式(13)の
を合わせて
を構成する。式(16)に
を代入すると,閉ループ系は
となる。そのブロック線図を図6.3に示す。
さて,
となる。ここで,
と計算できるから
と表される。したがって
を得る。ここで
となり,外乱の影響が抑制されていることと,式(14)が成り立つことが確認できる。また,式(17)からつぎが成り立つ。
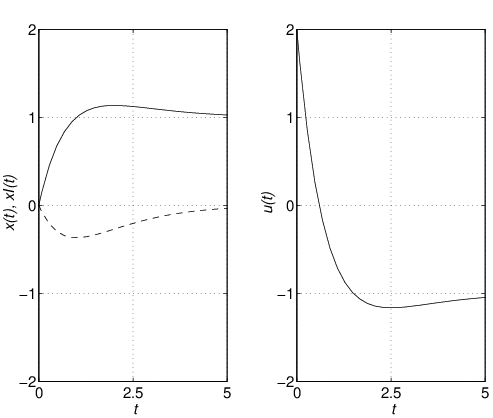
シミュレーション6.2
|
図6.4の下に次の問を設定していましたが,紙幅の関係で省略しました。
図6.4で,![]() ,
,![]() であることを確かめなさい。
であることを確かめなさい。
また,(19),(20),(21)におい![]() であることに注意してください。
であることに注意してください。
6.1.3 設定値を変更する
| 前節では,定値外乱の加わる1次系
に対して,制御目的
を達成する方法を学んだ。ここでは,任意の定数
を達成する問題を考える。この
この問題の解決のためには,外乱を抑制するための図6.4を,図6.5に示すように変更すればよい。実際,式(27)を
のような積分動作を導入すればよいことに気づくであろう。 式(25)と式(26)を合わせて
を構成する。いま,式(29)に
を代入すると
となる。
を得る。この第1行は,
を得る。ここで,設定値
また,つぎが成り立つ。
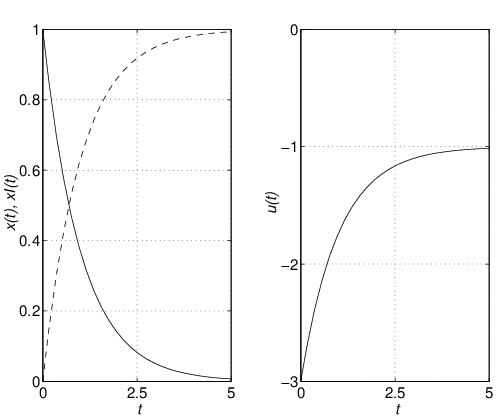
それでは,フィードフォワード項による速応性改善の効果をシミュレーションによって確かめよう。 シミュレーション6.3
問6.1 |
6.2 積分型コントローラ
6.2.1 積分動作を加えた状態フィードバック
| 次式で表される可制御かつ可観測で,
ここで,状態方程式には,操作入力
のように選び(
を達成したい。ここで,定数ベクトル
の関係を満足しているはずである。したがって,どのような
が成り立つように選ぶものとする。
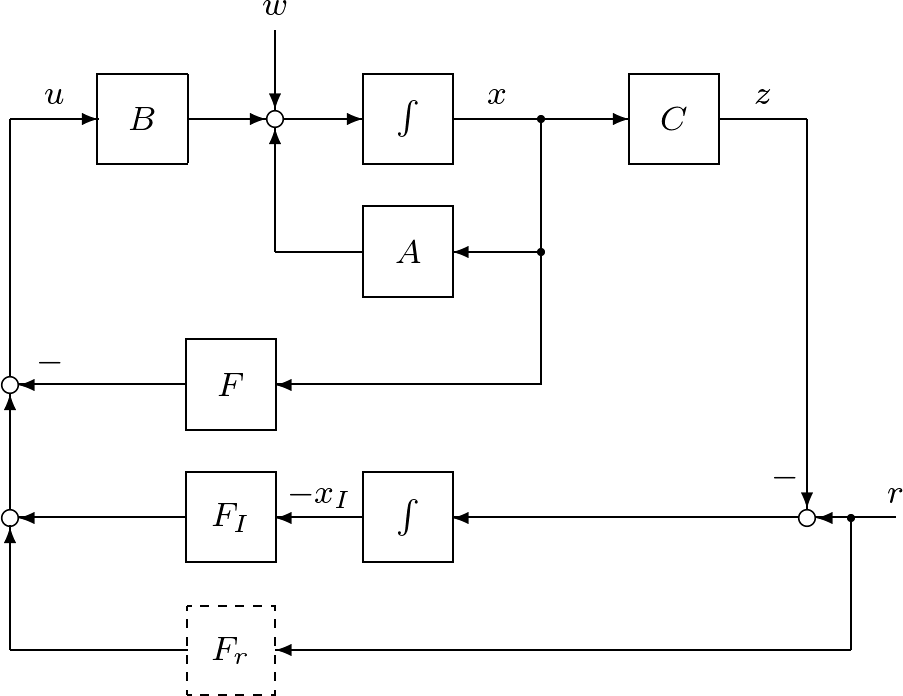
さて,制御目的(39)を達成するために,図6.8に示すような,つぎの積分動作を加えた状態フィードバックを考える。
ここで,第2項は積分動作を表している。このように
を得る。式(36)と式(43)を合わせて
を得る。式(44)に,式(42)すなわち
を代入すると,閉ループ系は,つぎのように表される。
いま,
よって,
を用いて
ここで,
のように計算される。ところで,式(46)から
を得る。この第1ブロック行は,式(40)より
となって,式(40)の第2ブロック行から制御目的(39)が成り立つ。また,式(50)の第2ブロック行から
を得る。ここで,設定値
のように表され,ここで,
|
6.2.2 積分動作を加えたオブザーバベース\,コントローラ
| 式(42)の代わりに,実際には,状態オブザーバ
の出力を用いて
を実施することになる。ここでの積分動作を加えたオブザーバベース\,コントローラは,式(56)を式(55)に代入した
と,式(43)を合わせて,つぎのように表される。
これによる閉ループ系は,式(56)を式(36)に代入した
と,式(43),(57)を合わせて
のように表される。そのブロック線図を図6.9に示す。
いま,閉ループ系(61)に,座標変換
を行えば
となり,閉ループ系の固有値は,積分動作を加えた状態フィードバックだけの閉ループ系の固有値と状態オブザーバの固有値からなる。 ここで,
すなわち
を得る。したがって,定値外乱が存在するときは状態オブザーバに関して定常偏差が残るにもかかわらず,制御目的(39)が成り立つことがわかる。また,フィードフォーワードゲイン |
6.3 LQI設計
| これまで,閉ループ系(18),(31),(46),(63)において, 制御目的(39)が達成されたとき成り立つ式(40)より
を得る( 偏差系E1: この両辺を微分すれば,状態変数の中の定数ベクトルを除くことができて 偏差系E2: を得る。さらに,式(36)と(38)をまとめた
から式(40)を引いて,つぎの関係式が成り立つ。
これに基づいて,偏差系E2に座標変換を行えば 偏差系E3: を得る。ここで,つぎの関係式を用いた。
問6.2 問6.3 例えば,偏差系E1に対して,状態フィードバック
を用いて,閉ループ系を安定化すれば, 以下に,偏差系E3をLQ制御により安定化して,積分動作を加えたオブザーバベース\,コントローラを構成する手順を示す。 アルゴリズム6.1 <LQI設計> 入力パラメータ1 出力パラメータ ステップ1 被制御変数の決定
ステップ2 偏差系の安定化 偏差系
を,状態フィードバック
によるLQ制御で安定化する。その際,評価関数としては
を用いる。ただし, さらに,
ステップ3 オブザーバゲイン 例えば,アルゴリズム5.2のステップ2を用いる。
を解いて,
ステップ4 LQIコントローラの構成
ただし
この積分動作を加えたオブザーバベース\,コントローラを簡潔にLQIコントローラ}(LQI controller),これによる制御方式をLQI制御(LQ control with integral action)と呼ぶ。 問6.4 |
 図6.1 外乱入力をもつ1次系
図6.1 外乱入力をもつ1次系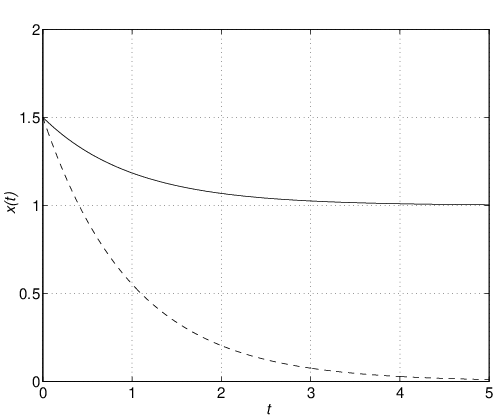
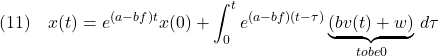
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \underbrace{ \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \end{array}\right] }_{\dot{x}_E(t)} = %\underbrace{ \left[\begin{array}{cc} a & 0 \\ 1 & 0 \end{array}\right] %}_{A_E} \underbrace{ \left[\begin{array}{c} x(t) \\ x_I(t) \end{array}\right] }_{x_E(t)} + %\underbrace{ \left[\begin{array}{c} b \\ 0 \end{array}\right] %}_{B_E} u(t) + \underbrace{ \left[\begin{array}{c} w \\ 0 \end{array}\right] }_{w_E} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ed7888e66cf423a299c78119493e2a8f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad u(t)=-fx(t) %\underbrace{ -f_Ix_I(t) %}_{+v(t)} =- \underbrace{ \left[\begin{array}{cc} f & f_I \end{array}\right] }_{F_E} \underbrace{ \left[\begin{array}{c} x(t) \\ x_I(t) \end{array}\right] }_{x_E(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5541d2dd02a7b6ebe166310f4c922b7f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \underbrace{ \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \end{array}\right] }_{\dot{x}_E(t)} = \underbrace{ \left[\begin{array}{cc} a-bf & -bf_I \\ 1 & 0 \end{array}\right] }_{A_{EF}} \underbrace{ \left[\begin{array}{c} x(t) \\ x_I(t) \end{array}\right] }_{x_E(t)} + \underbrace{ \left[\begin{array}{c} w \\ 0 \end{array}\right] }_{w_E} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9ce54a9bb373b31ef22c017c0033d328_l3.png)

![Rendered by QuickLaTeX.com \displaystyle{(23)\quad \left[\begin{array}{c} x(t) \\ x_I(t) \end{array}\right] \ \rightarrow\ \left[\begin{array}{c} 0 \\ \displaystyle{\frac{w}{bf_I}} \end{array}\right] \quad (t\rightarrow\infty) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-730cb6e0547a706ae11a604fcf3f76b4_l3.png)

![Rendered by QuickLaTeX.com \displaystyle{(31)\quad %\underbrace{ \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \end{array}\right] %}_{\dot{x}_E(t)} = \underbrace{ \left[\begin{array}{cc} a-bf & -bf_I \\ 1 & 0 \end{array}\right] }_{A_{EF}} %\underbrace{ \left[\begin{array}{c} x(t) \\ x_I(t) \end{array}\right] %}_{x_E(t)} + %\underbrace{ \left[\begin{array}{c} w \\ -r \end{array}\right] %}_{w_E} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-107de515677af73c8cfa3d74309054d6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(32)\quad \left[\begin{array}{c} x(t) \\ x_I(t) \end{array}\right] \ \rightarrow\ \underbrace{ \displaystyle{\frac{1}{bf_I}} \left[\begin{array}{cc} 0 & bf_I \\ -1 & a-bf \end{array}\right] }_{A_{EF}^{-1}} \left[\begin{array}{c} -w \\ r \end{array}\right] \quad (t\rightarrow\infty) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d1efa2ea9c0128df30789fc39ea551f4_l3.png)
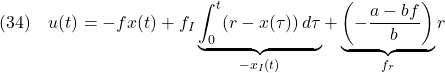
![Rendered by QuickLaTeX.com \displaystyle{(41)\quad {\rm rank}\, \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S}=n+m }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6d7d661fc9e59a3b704afda235a27be2_l3.png)
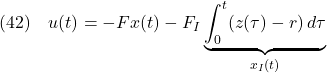
![Rendered by QuickLaTeX.com \displaystyle{(46)\quad %\underbrace{ \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \end{array}\right] %}_{\dot{x}_E(t)} = \underbrace{ \left[\begin{array}{cc} A-BF & -BF_I \\ C & 0 \end{array}\right] }_{A_{EF}} %\underbrace{ \left[\begin{array}{c} x(t) \\ x_I(t) \end{array}\right] %}_{x_E(t)} + %\underbrace{ \left[\begin{array}{c} w \\ -r \end{array}\right] %}_{w_E} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-eae149cb8e48771ddf2829382730be8f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(47)\quad A_{EF} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} - \left[\begin{array}{cc} B \\ 0 \end{array}\right] \left[\begin{array}{cc} F & F_I+I_m \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bdd5074b66a5f1df70acdb96f25154a5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(48)\quad \begin{array}{ll} A_{EF}^{-1} =& S^{-1}+ S^{-1} \left[\begin{array}{cc} B \\ 0 \end{array}\right] \left(I_m- \left[\begin{array}{cc} F & F_I+I_m \end{array}\right] S^{-1} \left[\begin{array}{cc} B \\ 0 \end{array}\right] \right)^{-1} \\[5mm] &\times \left[\begin{array}{cc} F & F_I+I_m \end{array}\right] S^{-1} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9d2c5a73b40a6bad18b71d793037dc0d_l3.png)
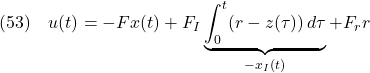
![Rendered by QuickLaTeX.com \displaystyle{(58)\quad \begin{array}{rl} \left[\begin{array}{c} \dot{\hat{x}}(t) \\ \dot{x}_I(t) \end{array}\right] =& \underbrace{ \left[\begin{array}{cc} A-HC_M-BF & -BF_I \\ 0(m\times n) & 0(m\times m) \end{array}\right] }_{A_K} \left[\begin{array}{c} \hat{x}(t) \\ x_I(t) \end{array}\right]\\[10mm] &+ \underbrace{ \left[\begin{array}{cc} H & 0(n\times m)\\ C_S & -I_m \end{array}\right] }_{B_K} \left[\begin{array}{c} y(t) \\ r \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0674921b2ea4d9a7a9554aeb4e94375f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(59)\quad u(t)= \underbrace{- \left[\begin{array}{cc} F & F_I \end{array}\right] }_{C_K} \left[\begin{array}{c} \hat{x}(t) \\ x_I(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1eaa990f79c14f18c22d28baecc3287b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(61)\quad \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \\ \dot{\hat{x}}(t) \end{array}\right] = \left[\begin{array}{ccc} A & -BF_I & -BF \\ C & 0 & 0 \\ HC_M & -BF_I & A-HC_M-BF \end{array}\right] \left[\begin{array}{c} x(t) \\ x_I(t) \\ \hat{x}(t) \end{array}\right] + \left[\begin{array}{c} w \\ -r \\ 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5628b37e548005d81b699f0317cfbcd2_l3.png)
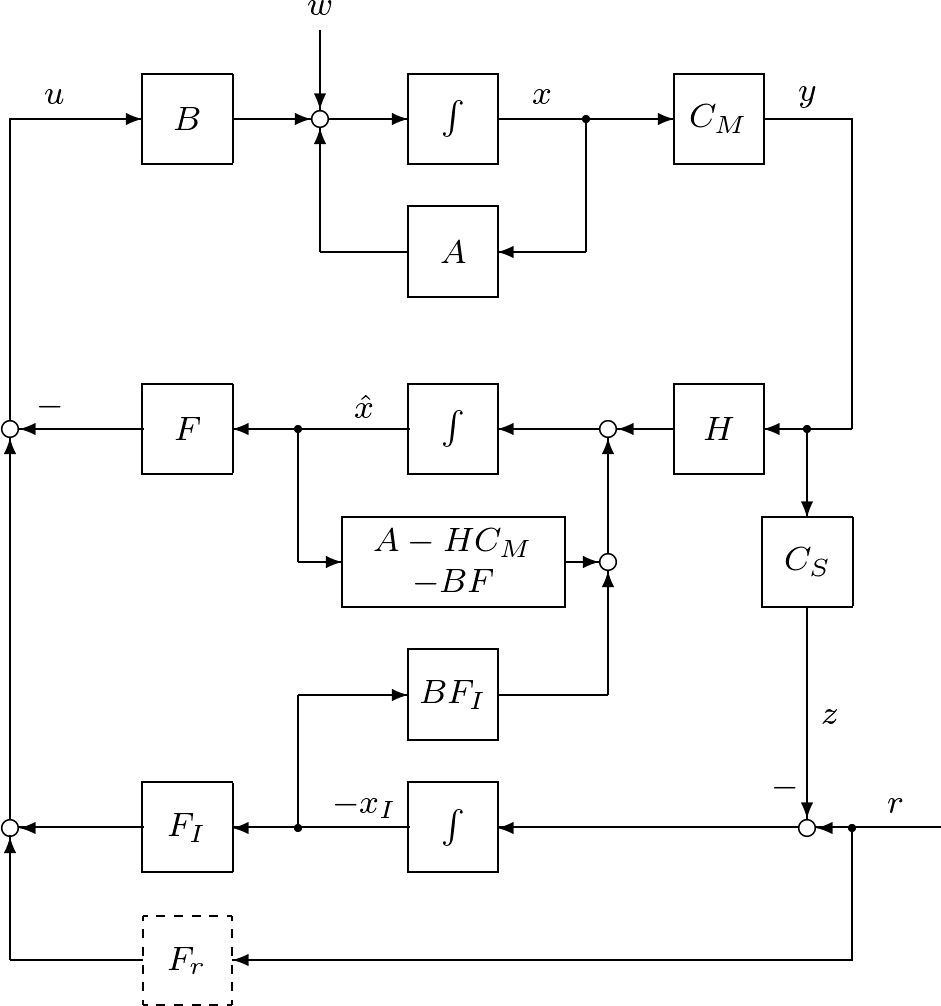
![Rendered by QuickLaTeX.com \displaystyle{(62)\quad \left[\begin{array}{c} x(t) \\ x_I(t) \\ e(t) \end{array}\right] = \left[\begin{array}{ccc} I_n & 0 & 0 \\ 0 & I_m & 0 \\ -I_n & 0 & I_n \end{array}\right] \left[\begin{array}{c} x(t) \\ x_I(t) \\ \hat{x}(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-398042fbd4912104fef837986adc51a1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(63)\quad \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \\\hline \dot{e}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc|c} A-BF & -BF_I & -BF \\ C & 0 & 0 \\\hline 0 & 0 & A-HC_M \end{array}\right] }_{ A_{EF}'= \left[\begin{array}{c|c} A_{EF} & - \left[\begin{array}{cc} B \\ 0 \end{array}\right] F \\[5mm] \hline 0 & \widehat{A} \end{array}\right] } \left[\begin{array}{c} x(t) \\ x_I(t) \\\hline e(t) \end{array}\right] + \left[\begin{array}{c} w \\ -r \\\hline -w \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b776ef380292f9c7b97e082e1356466d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(64)\quad \left[\begin{array}{c} x(t) \\ x_I(t) \\\hline e(t) \end{array}\right] \ \rightarrow\ \underbrace{ \left[\begin{array}{c|c} A_{EF}^{-1} & -A_{EF}^{-1} \left[\begin{array}{cc} B \\ 0 \end{array}\right] F\widehat{A}^{-1} \\[5mm]\hline 0 & \widehat{A}^{-1} \end{array}\right] }_{A_{EF}'\,^{-1}} \left[\begin{array}{c} -w \\ r \\\hline w \end{array}\right] \quad (t\rightarrow\infty) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3d3d576874ceeaf93880948df0adb803_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(69)\quad \frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] %}_{x_E(t)-x_{E\infty}} = \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E1}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] %}_{x_E(t)-x_{E\infty}} + \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E1}} (u(t)-u_\infty) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f6e3bc338005f728c3c6b147eb039e9e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(70)\quad \frac{d}{dt} %\underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] %}_{\dot{x}_E(t)} = \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E2}} %\underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] %}_{\dot{x}_E(t)} + \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E2}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-966078beee574786867caed4fcd2d943_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(71)\quad \left[\begin{array}{c} {\dot x}(t)-w \\ z(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \left[\begin{array}{c} x(t) \\ u(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1426f7e0895fd79de17dc34732b3e43c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(72)\quad \left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c1612c9c215faae7214a621c77652b77_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(73)\quad \frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} + \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-61e355172bd112774aad674a10e1d6b1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(74)\quad \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E2}} \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-47811d4d699fd4de1d937f73c0245ddb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(75)\quad \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E2}} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E3}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-46729c351e496ba40060fc93a706a112_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(76)\quad \underbrace{ \left[\begin{array}{cc} 0 & I_m \end{array}\right] }_{C_{E2}} \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} = \underbrace{ \left[\begin{array}{cc} C & 0 \end{array}\right] }_{C_{E3}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4ea560477a3448b751379c9a95240132_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(78)\quad \frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} + \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-40c26e612ca99e6fd4cd79c47fb7d193_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(80)\quad \int_0^\infty \left( \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right]^T Q_E \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] +{\dot u}^T(t)R_E{\dot u}(t)\right)\,dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-91e30617eef32873dec337f41b4b0942_l3.png)