基礎事項

投稿日時: 投稿者:

[0] 表計算ソフトEXCELの基礎事項を、初歩的な統計計算を通して説明します。

[1] 次の集計表を作成しましょう。

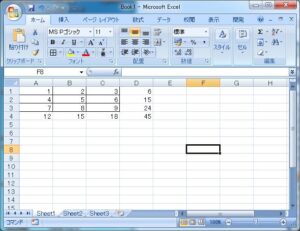
各列の集計は、まず、セルA4に「=sum(A1:A3)」を入れ、これをセルB4,C4に、Copy & Paste （以下、C&P）します。このとき、セルB4,C4はそれぞれ、「=sum(B1:B3)」、「=sum(C1:C3)」
となっており、和をとる列が自動的に変更されていることに注意してください。同様に、各行の集計は、まず、セルD1に「=sum(A1:C1)」を入れ、これをセルD2,D3,D4にC&Pします。表計算の利点はデータ更新時の再計算にあります。適当に、データを変更して、再計算の便利さを確かめてみましょう。

[2] 次の成績データの偏差値を計算してください。

{(i,x_i)|i=1,…,10}={(1,89),(2,70),(3,63),(4,100),(5,81),(6,30),(7,56),(8,77),(9,90),(10,63)}

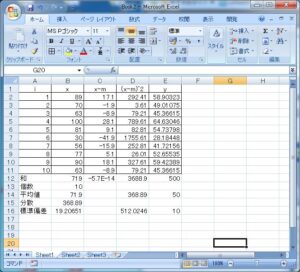
まず、留意すべきは、列Aの入力方法です。セルA2に初期値「1」を入力し、セルA3に「=A2+1」を入力し、これを領域A4:A11にC&Pします。

つぎに、和、個数、平均値、分散、標準偏差をそれぞれ次のように入力して求めておきます。

セルB12　⇒　=sum(B2:B11)
セルB13　⇒　=count(B2:B11)
セルB14　⇒　=average(B2:B11)
セルB15　⇒　=varp(B2:B11)
セルB16　⇒　=stdevp(B2:B11)

ここで、平均値と分散は、次式で与えられるのでした。

\displaystyle{m_x=\frac{1}{n}\sum_{i=1}^{n}x_i}
\displaystyle{\sigma_x^2=\frac{1}{n}\sum_{i=1}^{n}(x_i-m)^2}

偏差値とは，平均値50，標準偏差10となるように線形変換した値のことで、次式で計算されます。

\displaystyle{y_i=10\frac{x_i-m_x}{\sigma_x}+50}

列C,列D,列Eの作成法は、次の通りです。セルC2,D2,D2に、次のように入力します。

セルC2　⇒　=B2-$B$14
セルD2　⇒　=C2^2
セルE2　⇒　=10*C2/$B$16+50

ここで、セルB14とB16の参照は、それぞれ絶対アドレス$B$14と$B$16を用いることに留意してください。これらを下方にC&Pします。ちなみに、分布の形を変えないで60点以上が合格となるように、新しい平均値，標準偏差の値を調整して、ゲタをはかせることができます。

参考までに、平均値と分散の漸化式（オンライン計算式）を与えておきます。

\begin{array}{lll} m_n&=&\frac{1}{n}\sum_{i=1}^{n}x_i \nonumber\\ &=&\frac{n-1}{n}\left(\frac{1}{n-1}\sum_{i=1}^{n-1}x_i\right)+\frac{1}{n}x_n \nonumber\\ &=&\frac{n-1}{n}m_{n-1}+\frac{1}{n}x_n\nonumber \end{array}

\begin{array}{lll} \sigma_n^2&=&\frac{1}{n}\sum_{i=1}^{n}(x_i-m_n)^2\nonumber\\ &=&\frac{1}{n}\sum_{i=1}^{n}x_i^2-m_n^2\nonumber\\ &=&\frac{n-1}{n}\left(\frac{1}{n-1}\sum_{i=1}^{n-1}x_i^2\right)+\frac{1}{n}x_n^2 -\left(\frac{n-1}{n}m_{n-1}+\frac{1}{n}x_n\right)^2\nonumber\\ &=&\frac{n-1}{n}(\sigma_{n-1}^2+m_{n-1}^2)+\frac{1}{n}x_n^2- \left(\frac{(n-1)^2}{n^2}m_{n-1}^2+2\frac{n-1}{n^2}m_{n-1}x_n+\frac{1}{n^2}x_n^2\right)\nonumber\\ &=&\frac{n-1}{n}\sigma_{n-1}^2+\frac{n-1}{n^2}m_{n-1}^2 -2\frac{n-1}{n^2}m_{n-1}x_n+\frac{n-1}{n^2}x_n^2\nonumber\\ &=&\frac{n-1}{n}\sigma_{n-1}^2+\frac{n-1}{n^2}(x_n-m_{n-1})^2\nonumber \end{array}

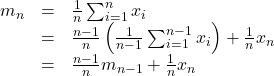
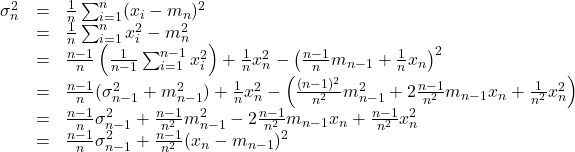
それでは、与えられたデータの棒グラフを描きましょう。「挿入」、「グラフ」と進んで、「縦棒」、「2D-縦棒」を選びます。

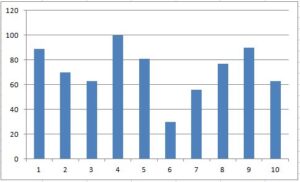
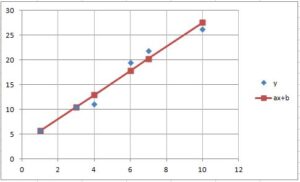
[4] 次の計測データの回帰直線を計算してください。

{(x_i,y_i)|i=1,…,6}={(1,5.7),(3,10.4),(4,11.1),(6,19.5),(7,21.8),(10,26.2)}

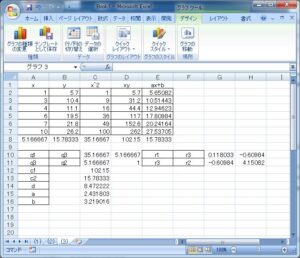
ここで、行列（領域C10:D11）の逆行列を領域G10:H11に計算しています。そのためには、

セルG10　⇒　=MINVERSE(C10:D11)

を入力し、領域C10:D11を選択し、窓fxにカーソルを合わせ、”[Ctrl] + [Shift] + [Enter]” を入力します。

次に、この逆行列とベクトル（領域C12:C13）の掛け算を領域C15:C16に計算しています。そのためには、

セルC15　⇒　=MMULT(G10:H11,C12:C13)

を入力し、領域C15:C16を選択し、窓fxにカーソルを合わせ、”[Ctrl] + [Shift] + [Enter]” を入力します。

それでは、計算式の詳細を説明します。回帰直線ax+bは、次の最小化問題を解いて得られます。

\displaystyle{\min_{a,b} \frac{1}{n}\sum_{i=1}^{n}(y_i-ax_i-b)^2}

この解は、次式で与えられます。

\displaystyle{a=\frac{1}{d}(c_1q_2-c_2q_3)},\quad \displaystyle{b=\frac{1}{d}(-c_1q_3+c_2q_1)}

ただし、d=q_1q_2-q_3^2、また

\displaystyle{q_1=\frac{1}{n}\sum_{i=1}^{n}x_i^2},\quad \displaystyle{q_2=1},\quad \displaystyle{q_3=\frac{1}{n}\sum_{i=1}^{n}x_i}
\displaystyle{c_1=\frac{1}{n}\sum_{i=1}^{n}x_iy_i},\quad \displaystyle{c_2=\frac{1}{n}\sum_{i=1}^{n}y_i}

実際、目的関数を

\displaystyle{J(a,b)=\frac{1}{n}\sum_{i=1}^{n}(y_i-ax_i-b)^2}

とおくと、これが極値をとる条件は

\displaystyle{\left\{\begin{array}{l} \frac{\partial J}{\partial a}=\frac{2}{n}\sum_{i=1}^{n}(y_i-ax_i-b)(-x_i)=0\\ \frac{\partial J}{\partial b}=\frac{2}{n}\sum_{i=1}^{n}(y_i-ax_i-b)(-1)=0 \end{array}\right.}

となります。これは、上記の記号を用いて

\displaystyle{\left\{\begin{array}{l} -c_1+q_1a+q_3b=0\\ -c_2+q_3a+q_2b=0 \end{array}\right.}

のように書けます。これを行列表示すると

\left[\begin{array}{cc} q_1 & q_3 \\ q_3 & q_2 \end{array}\right] \left[\begin{array}{cc} a \\ b \end{array}\right] = \left[\begin{array}{cc} c_1 \\ c_2 \end{array}\right]

となって、aとbは、次式で与えられるからです。

\left[\begin{array}{cc} a \\ b \end{array}\right] = \frac{1}{d} \left[\begin{array}{cc} q_2 & -q_3 \\ -q_3 & q_1 \end{array}\right] \left[\begin{array}{cc} c_1 \\ c_2 \end{array}\right]

ちなみに、SCILABでは、次式で計算されます。

–> A=[[1 3 4 6 7 10]’ ones(6,1)];
–> b=[5.7 10.4 11.1 19.5 21.6 26.2]’;
–> A\b

それでは、与えられたデータの折れ線グラフを描きましょう。「挿入」、「グラフ」と進んで、そのグラフをと使えばよいでしょうか？実は「散布図」を選びます。グラフの背景はデフォールトが灰色の場合、白色に変更しましょう。