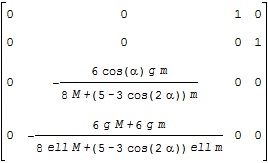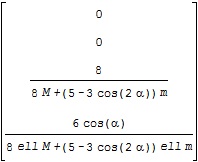[1] 台車駆動型倒立振子CIP
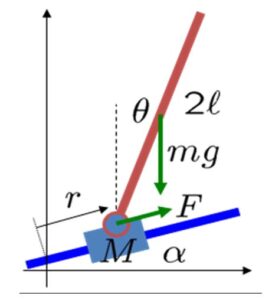
上図のように、倒立振子を軸支した台車を、傾斜角 ![]() を持つレール上に載せた状況を考えます。このとき、まず運動方程式を導出し,これを平衡状態まわりで線形化し、状態方程式と出力方程式からなる状態空間表現を得ましょう。
を持つレール上に載せた状況を考えます。このとき、まず運動方程式を導出し,これを平衡状態まわりで線形化し、状態方程式と出力方程式からなる状態空間表現を得ましょう。
以下では、倒立振子となる棒は長さ ![]() 、質量
、質量 ![]() の一様な剛体で、台車の質量は
の一様な剛体で、台車の質量は ![]() とします。棒の鉛直線からの傾きを
とします。棒の鉛直線からの傾きを ![]() 、台車のレールに沿う変位を
、台車のレールに沿う変位を ![]() 、台車を駆動する力
、台車を駆動する力 ![]() とします。また,簡単のため、軸は、棒の端(棒の重心から
とします。また,簡単のため、軸は、棒の端(棒の重心から ![]() の位置)に取り付けられ、台車の重心と一致し,駆動力の作用点でもあるとします。なお、この制御対象に対して、計測可能な物理変数は、
の位置)に取り付けられ、台車の重心と一致し,駆動力の作用点でもあるとします。なお、この制御対象に対して、計測可能な物理変数は、![]() と
と ![]() であるとします。
であるとします。
まず、軸の位置のx座標を ![]() 、y座標を
、y座標を ![]() とすると
とすると
![]()
![]()
となり、台車の運動エネルギー ![]() と位置エネルギー
と位置エネルギー ![]() は
は
![]()
![]()
のように表されます。また 、棒の重心位置のx座標を ![]() 、y座標を
、y座標を ![]() とすると
とすると
![]()
![]()
となり、棒の運動エネルギー ![]() と位置エネルギー
と位置エネルギー ![]() は
は
![]()
![]()
のように表されます。ここで、![]() は重心周りの慣性モーメントを表し
は重心周りの慣性モーメントを表し
![]()
です。以上の準備の下で、ラグランジュの運動方程式は,ラグランジアンを
![]()
として
![]()
![]()
のように与えられます。
それでは、MAXIMAを用いて、制御対象の運動方程式を導出してみましょう。
/*cip.wxm*/
dr:’diff(r(t),t); ddr:’diff(r(t),t,2);
dth:’diff(th(t),t); ddth:’diff(th(t),t,2);
x0:r(t)*cos(alpha); y0:r(t)*sin(alpha);
T0:(1/2)*M*(diff(x0,t)^2+diff(y0,t)^2);
V0:M*g*y0;
x1:x0+ell*sin(th(t)); y1:y0+ell*cos(th(t));
J1:(1/3)*m*ell^2;
T1:(1/2)*m*(diff(x1,t)^2+diff(y1,t)^2)+(1/2)*J1*dth^2;
V1:m*g*y1;
L:T0+T1-V0-V1;
LE1:diff(diff(L,dr),t)-diff(L,r(t))=F,trigreduce,ratsimp;
LE2:diff(diff(L,dth),t)-diff(L,th(t))=0,trigreduce,ratsimp;
これを実行すると、LE1として、次の結果を得ます。
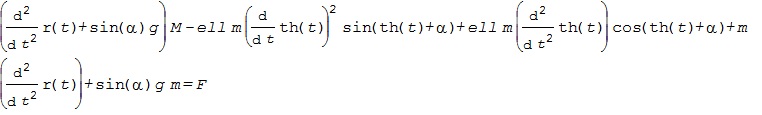
また、LE2として、次の結果を得ます。
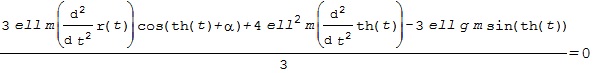
これらを行列表示して、制御対象の運動方程式として
![]()
を得ます。これを行列表示すると
![]()
ただし
![]()
![]()
となります。これから、制御対象の非線形状態方程式
![]()
すなわち、状態変数ベクトルと入力変数を
![Rendered by QuickLaTeX.com \xi= \left[\begin{array}{c} \xi_1 \\ \xi_2 \end{array}\right] = \left[\begin{array}{c} r \\ \theta \\ \dot{r} \\ \dot{\theta} \end{array}\right],\ \zeta=F](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b0388783ea269a17a07e587b3858ec56_l3.png)
と定義するとき、制御対象の非線形状態方程式
![]()
ただし
![Rendered by QuickLaTeX.com \displaystyle{ f(\xi,\zeta)= \left[\begin{array}{c} f_1(\xi,\zeta) \\ f_2(\xi,\zeta) \\ f_3(\xi,\zeta) \\ f_4(\xi,\zeta) \end{array}\right]= \left[\begin{array}{c} f_1(r,\theta,\dot{r},\dot{\theta},F) \\ f_2(r,\theta,\dot{r},\dot{\theta},F) \\ f_3(r,\theta,\dot{r},\dot{\theta},F) \\ f_4(r,\theta,\dot{r},\dot{\theta},F) \end{array}\right]= \left[\begin{array}{c} {\xi}_2 \\ M^{-1}(\xi_1)(e_1\zeta-C(\xi_1){\xi}_2-G(\xi_1)) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-00729f634057c8db1004528a22f4155a_l3.png)
を得ます。
さて、制御対象の平衡状態 ![]() と、これを実現する平衡入力
と、これを実現する平衡入力 ![]() を考えます。これらは、運動方程式において、加速度=0(
を考えます。これらは、運動方程式において、加速度=0(![]() )とおいた、
)とおいた、
![]()
すなわち
![]()
を解いて得られます。これより、平衡状態 ![]() と、これを実現する平衡入力
と、これを実現する平衡入力 ![]() として
として
![Rendered by QuickLaTeX.com \xi^*= \left[\begin{array}{c} \xi^*_1 \\ \xi^*_2 \end{array}\right]= \left[\begin{array}{c} r^* \\ \theta^* \\ \dot{r}^* \\ \dot{\theta}^* \end{array}\right]= \left[\begin{array}{c} 0 \\ 0 \\ 0 \\ 0 \end{array}\right]\ or\ \left[\begin{array}{c} 0 \\ \pi \\ 0 \\ 0 \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8f1c442239e419bdc4574e49225aa032_l3.png)
![]()
を得ます。このとき、明らかに、次式が満足されています。
![]()
この平衡状態(と平衡入力)まわりで、非線形状態方程式を、線形化(1次近似)します。
![]()
ただし
![Rendered by QuickLaTeX.com \displaystyle{ \frac{\partial f(\xi^*,\zeta^*)}{\partial\xi} =\left.\left[\begin{array}{cccc} \frac{\partial f_1}{\partial r} & \frac{\partial f_1}{\partial\theta} &\frac{\partial f_1}{\partial\dot{r}} & \frac{\partial f_1}{\partial\dot{\theta}} \\ \frac{\partial f_2}{\partial r} & \frac{\partial f_2}{\partial\theta} &\frac{\partial f_2}{\partial\dot{r}} & \frac{\partial f_2}{\partial\dot{\theta}} \\ \frac{\partial f_3}{\partial r} & \frac{\partial f_3}{\partial\theta} &\frac{\partial f_3}{\partial\dot{r}} & \frac{\partial f_3}{\partial\dot{\theta}} \\ \frac{\partial f_4}{\partial r} & \frac{\partial f_4}{\partial\theta} &\frac{\partial f_4}{\partial\dot{r}} & \frac{\partial f_4}{\partial\dot{\theta}} \end{array}\right] \right|_{r=0,\theta=\theta^*,\dot{r}=0,\dot{\theta}=0,F=F^*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3287a406e47f96caee26fb5d7e39129a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \frac{\partial f(\xi^*,\zeta^*)}{\partial\zeta} =\left.\left[\begin{array}{cccc} \frac{\partial f_1}{\partial F} \\ \frac{\partial f_2}{\partial F} \\ \frac{\partial f_3}{\partial F} \\ \frac{\partial f_4}{\partial F} \end{array}\right] \right|_{r=0,\theta=\theta^*,\dot{r}=0,\dot{\theta}=0,F=F^*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bab1bcd48b67405a9e0d85d026eac2ef_l3.png)
これから、![]() に注意して、制御対象の線形状態方程式
に注意して、制御対象の線形状態方程式
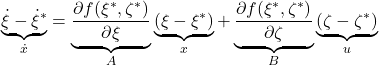
すなわち
![Rendered by QuickLaTeX.com \underbrace{ \frac{d}{dt} \left[\begin{array}{c} r-r^* \\ \theta-\theta^* \\ \dot{r}-\dot{r}^* \\ \dot{\theta}-\dot{\theta}^* \end{array}\right] }_{\dot{x}}= \underbrace{ \left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 0 & a_{32} & 0 & 0\\ 0 & a_{42} & 0 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} r-r^* \\ \theta-\theta^* \\ \dot{r}-\dot{r}^* \\ \dot{\theta}-\dot{\theta}^* \end{array}\right] }_{x} +\underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ b_{32} \\ b_{42} \end{array}\right] }_{B} \underbrace{ (\dot{\zeta}-\dot{\zeta}^*) }_{u}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e1f883a4b1a3ed2618abc05e42a9c6ff_l3.png)
を得ます。
以上の計算をMAXIMAを用いて実行するには、次のプログラムを作成します。
/*cip.wxm*/
:
sol:solve([LE1,LE2],[ddr,ddth]);
f:matrix([dr],[dth],[rhs(sol[1][1])],[rhs(sol[1][2])]);
a31:diff(f[3,1],r(t)); a32:diff(f[3,1],th(t));
a33:diff(f[3,1],dr); a34:diff(f[3,1],dth);
a41:diff(f[4,1],r(t)); a42:diff(f[4,1],th(t));
a43:diff(f[4,1],dr); a44:diff(f[4,1],dth);
b3:diff(f[3,1],F); b4:diff(f[4,1],F);
Fs:(M+m)*g*sin(alpha);
A:matrix([0,0,1,0],[0,0,0,1],[a31,a32,a33,a34],[a41,a42,a43,a44]);
A1:A,th(t)=0,F=Fs,trigreduce,ratsimp;
A2:A,th(t)=%pi,F=Fs,trigreduce,ratsimp;
B:matrix([0],[0],[b3],[b4]);
B1:B,th(t)=0,F=Fs,trigreduce,ratsimp;
B2:B,th(t)=%pi,F=Fs,trigreduce,ratsimp;
ここで、![]() に対応する平衡状態周りの線形状態方程式のA行列がA1、B行列がB1で、それぞれ次のような結果となります。
に対応する平衡状態周りの線形状態方程式のA行列がA1、B行列がB1で、それぞれ次のような結果となります。
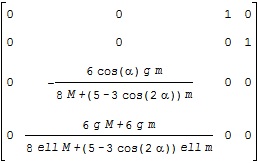
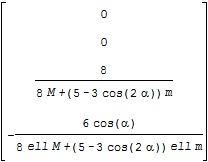
また、![]() に対応するA行列がA2、B行列がB2で、それぞれ次のような結果となります。
に対応するA行列がA2、B行列がB2で、それぞれ次のような結果となります。