[0] MAXIMAを用いて、倒立振子の運動方程式を導出し、非線形状態方程式を求め、これを平衡状態まわりで線形化(1次近似)し、線形状態方程式を求めます。
そのために必要となるのが、ベクトル値多変数関数
![]()
の ![]() まわりの1次近似式
まわりの1次近似式
![]()
です。これは、たとえば、 ![]() のとき、次のように計算されます。
のとき、次のように計算されます。
![Rendered by QuickLaTeX.com \begin{array}{lll} \underbrace{ \left[\begin{array}{cc} f_1(x_1,x_2)\\ f_2(x_1,x_2) \end{array}\right] }_{f(x)}\nonumber\\ \simeq \left[\begin{array}{cc} f_1(a_1,a_2)+\frac{\partial\,f_1(a_1,a_2)}{\partial\,x_1}(x_1-a_1)+\frac{\partial\,f_1(a_1,a_2)}{\partial\,x_2}(x_2-a_2)\\ f_2(a_1,a_2)+\frac{\partial\,f_2(a_1,a_2)}{\partial\,x_1}(x_1-a_1)+\frac{\partial\,f_2(a_1,a_2)}{\partial\,x_2}(x_2-a_2) \end{array}\right]\nonumber\\ = \underbrace{ \left[\begin{array}{cc} f_1(a_1,a_2)\\ f_2(a_1,a_2) \end{array}\right] }_{f(a)} + \underbrace{ \left[\begin{array}{cc} \frac{\partial f_1(a_1,a_2)}{\partial x_1}&\frac{\partial f_1(a_1,a_2)}{\partial x_2}\\ \frac{\partial f_2(a_1,a_2)}{\partial x_1}&\frac{\partial f_2(a_1,a_2)}{\partial x_2} \end{array}\right] }_{\frac{\partial\,f(a)}{\partial\,x}} \underbrace{ \left[\begin{array}{cc} x_1-a_1\\ x_2-a_2\nonumber \end{array}\right] }_{x-a}\nonumber \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-67d6279d41d4a2c86662d65aeca81a64_l3.png)
[1] 振り子PEN
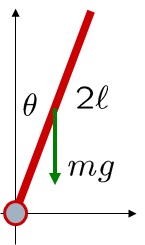
上図の振り子PENを見てください。長さ、![]() の振り子の重心周りの慣性モーメントは
の振り子の重心周りの慣性モーメントは
![]()
のように計算できます。これから,振り子の軸まわりの慣性モーメントは、平行軸の定理を使って
![]()
のように与えられます。また、軸まわりのトルクは
![]()
のように表わされます。したがって、振り子の運動方程式は、次式となります。
![]()
それでは、この運動方程式を、ラグランジュの方法で導出してみます。その手順は次のようになります。
まず、振り子の重心のx、y座標と、軸周りの慣性モーメントは
![]()
![]()
![]()
ですから、運動エネルギーと位置エネルギーは
![]()
![]()
となり、ラクランジアンを
![]()
として、ラグランジュの運動方程式は
![]()
となります。これから振り子の運動方程式が得られます。
それでは、MAXIMAを用いて、振り子の運動方程式を導出してみましょう。
/*pen.wxm*/
dth:’diff(th(t),t);
ddth:’diff(th(t),t,2);
x:ell*sin(th(t));
y:ell*cos(th(t));
J:(1/3)*m*ell^2;
T:(1/2)*m*(diff(x,t)^2+diff(y,t)^2)+(1/2)*J*dth^2;
V:m*g*ell*cos(th(t));
L:T-V;
LE:diff(diff(L,dth),t)-diff(L,th(t))=0,trigreduce;
sol:solve(LE,ddth);
次に、2階微分を含む運動方程式を1階微分だけの連立微分方程式に変換し、これをベクトル表示します。
![]()
すなわち、状態変数ベクトル
![]()
を定義するとき、振り子の非線形状態方程式
![]()
ただし
![]()
が得られました。ところで、振り子は2つの平衡状態(物理的な釣り合いの状態)を持ちます。
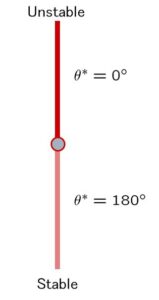
これらは次のように特徴付けられます。
![]()
すなわち
![Rendered by QuickLaTeX.com \underbrace{ \left[\begin{array}{c} \dot{\theta}^* \\ \dot{\omega}^* \end{array}\right] }_{\dot{\xi}^*} = \underbrace{ \left[\begin{array}{c} \omega^* \\ \frac{3g}{4\ell}\sin\theta^* \end{array}\right] }_{f(\xi^*)} = \underbrace{ \left[\begin{array}{c} 0 \\ 0 \end{array}\right] }_{0} \ \Rightarrow\ \xi^* = \left[\begin{array}{c} \theta^* \\ \omega^* \end{array}\right] = \left[\begin{array}{c} 0 \\ 0 \end{array}\right] \,or\, \left[\begin{array}{c} \pi \\ 0 \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cb697f6e9356b7da4dbf07362adaa686_l3.png)
そこで、振り子の非線形状態方程式を、平衡状態まわりで線形化(1次近似)します。
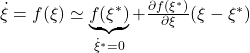
ただし
![Rendered by QuickLaTeX.com \displaystyle{ \frac{\partial f(\xi^*)}{\partial\xi}=\left.\left[\begin{array}{cc} \frac{\partial f_1}{\partial\theta} & \frac{\partial f_1}{\partial\omega} \\ \frac{\partial f_2}{\partial\theta} & \frac{\partial f_2}{\partial\omega} \end{array}\right] \right|_{\theta=\theta^*,\omega=0}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dcbf2bcb28e293a5f81e0e8bee5efa92_l3.png)
これから、振り子の線形状態方程式
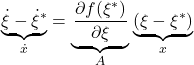
すなわち
![Rendered by QuickLaTeX.com \underbrace{ \frac{d}{dt} \left[\begin{array}{c} \theta-\theta^* \\ \omega-\omega^* \end{array}\right] }_{\dot{x}}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ \frac{3g}{4\ell}\cos\theta^* & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \theta-\theta^* \\ \omega-\omega^* \end{array}\right] }_{x}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1112619eccc3155d42b3e7a0f78a9753_l3.png)
を得ます。以上の計算をMAXIMAを用いて実行するには、次のコマンドを与えます。
f:matrix([dth],[rhs(sol[1])]);
A:matrix([diff(f[1,1],th(t)),diff(f[1,1],dth)],[diff(f[2,1],th(t)),diff(f[2,1],dth)]);
A1:A,th(t)=0;
A2:A,th(t)=%pi;