制御系CADに関わる数値計算では実行列の特異値分解(Singular-Value Decomposition, SVD)を多用しますが、データ駆動分野の計算でも基盤技術となっています。
●いまデータは次の複素行列にまとめられているとします。
![]()
ここで列ベクトル![]() はn次元数ベクトルですが、データ駆動分野では、nの値は数個ではなく、数千、数万のオーダーになります。
はn次元数ベクトルですが、データ駆動分野では、nの値は数個ではなく、数千、数万のオーダーになります。
●![]() をサイズ
をサイズ![]() の複素行列(
の複素行列(![]() )とします。このとき、ユニタリ行列
)とします。このとき、ユニタリ行列![]() と
と![]() が存在して
が存在して
![]()
が成り立ちます(![]() )。ここで、実行列
)。ここで、実行列![]() は次のように表されます。
は次のように表されます。
![]()
![]()
MATLABのコマンドでは、次のように求めます。
>> [U,S,V]=svd(X)
●いま![]() とします。このとき(2)は次式となります。
とします。このとき(2)は次式となります。
![Rendered by QuickLaTeX.com \displaystyle{(3.1)\quad X= \underbrace{\left[\begin{array}{cc} U_1 & U_2 \end{array}\right]}_{U} \underbrace{\left[\begin{array}{cc} \Sigma_1 \\ 0_{n-m\times m} \end{array}\right]}_{\Sigma}V^H =U_1\Sigma_1V^H }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-99bd7ee8f04376d8692adff04183fc9d_l3.png)
![]()
MATLABのコマンドでは、次のように求めます。
>> [U1,S1,V]=svd(X,’econ’)
(2)の場合は![]() は大規模な行列となりますが、(3)の場合はスリムな行列となりますので、Economic SVDと呼ぶことがあります。
は大規模な行列となりますが、(3)の場合はスリムな行列となりますので、Economic SVDと呼ぶことがあります。
●いま実効階数を![]() とします。すなわち微小な
とします。すなわち微小な![]() に対して
に対して
![]()
とします。このとき(3)から次式のように近似できます。
![Rendered by QuickLaTeX.com \displaystyle{(5.1)\quad X\approx \widetilde{X}= \underbrace{\left[\begin{array}{cc} \widetilde{U} & \cdot \end{array}\right]}_{U} \underbrace{\left[\begin{array}{cc} \widetilde{\Sigma} & 0_{r\times m-r} \\ 0_{n-r\times r} & 0_{n-r\times m-r} \end{array}\right]}_{\Sigma'} \underbrace{\left[\begin{array}{c} \widetilde{V}^H\\ \cdot \end{array}\right]}_{V^H} =\widetilde{U}\widetilde{\Sigma}\widetilde{V}^H }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-50accba44fba6606c36c904e16bc41ef_l3.png)
![]()
●(2.1)、(3.1)、(5.1)の関係はダイアディック形式を用いて次のように表されます。
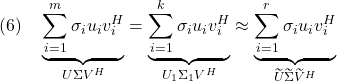
●相関行列![]() または
または![]() は、(3.1)より、次式のように表されます。
は、(3.1)より、次式のように表されます。
![Rendered by QuickLaTeX.com \displaystyle{(7.1)\quad \begin{array}{l} XX^H=U\left[\begin{array}{cc} \Sigma_1 \\ 0_{n-m\times m} \end{array}\right] \underbrace{V^HV}_{I_m}\left[\begin{array}{cc} \Sigma_1 & 0_{m\times n-m} \end{array}\right] U^H\\=U\left[\begin{array}{cc} \Sigma_1^2 & 0_{m\times n-m} \\ 0_{n-m\times m} & 0_{n-m\times n-m} \end{array}\right] U^H \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-37129f9819eafc06f911de1c423061d5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7.2)\quad X^HX=V\left[\begin{array}{cc} \Sigma_1 & 0_{m\times n-m} \end{array}\right] \underbrace{U^HU}_{I_n}\left[\begin{array}{cc} \Sigma_1 \\ 0_{n-m\times m} \end{array}\right] V^H=V\Sigma_1^2 V^H }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-826d5fbe94126670ef95066af033718f_l3.png)
これらより
![]()
![]()
すなわち、非零の特異値は相関行列![]() または
または![]() の固有値の正の平方根です。もし
の固有値の正の平方根です。もし![]() の場合は
の場合は![]() の特異値は
の特異値は![]() の固有値の絶対値となります。これはスカラの場合、次式を意味しています。
の固有値の絶対値となります。これはスカラの場合、次式を意味しています。
![]()
データ駆動分野では、nの値は数個ではなく、数千、数万のオーダーになります。一方、mの値はそのように大きな値とはなりません。したがって、(8.2)の小規模な固有値問題を解いて![]() と
と![]() を求め、(3.1)に基づいて、(8.1)の大規模な固有値問題の固有ベクトルの一部
を求め、(3.1)に基づいて、(8.1)の大規模な固有値問題の固有ベクトルの一部![]() を、次式により求めることが行われます。
を、次式により求めることが行われます。
![]()
(5.1)に基づく場合は次式となります。
![]()
このような手法はスナップショットと呼ばれています。
●観測データを行ベクトルとしてもつ![]() を考えます。
を考えます。
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad X=\left[\begin{array}{c} X_{11},\cdots,X_{1m}\\ \vdots\\ %X_{i1},\cdots,X_{im}\\ %\vdots\\ X_{n1},\cdots,X_{nm}\\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-191eb11d289ee99d4f776f71f3262037_l3.png)
ここで、![]() 回の観測が行われ、各観測では
回の観測が行われ、各観測では![]() 個のデータを得るものとしています。これから
個のデータを得るものとしています。これから
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \bar{X}=\left[\begin{array}{c} 1\\ \vdots\\ 1 \end{array}\right] \left[\begin{array}{c} \displaystyle{\frac{1}{n}\sum_{i=1}^nX_{i1},\cdots,\frac{1}{n}\sum_{i=1}^nX_{im}} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-992a3a3cd6f8f8980920c01cb001b6df_l3.png)
を引いた行列![]() の特異値分解を
の特異値分解を
![]()
とします。このとき、共分散行列は
![]()
のように表されます。すなわち共分散行列の主成分ベクトルと、その方向に沿う不変分散値が、行列![]() の特異値分解から得られることに留意します。
の特異値分解から得られることに留意します。