予備的考察
BackSteppingの邦訳は、読み方のバックステッピング以外には適切なものがないようですが、非線形系に対する一つの制御方式を表しています。そこで、以下ではBackSteppingをBS制御と呼ぶことにします。
BS制御の基本的なアイデアを、次の例を用いて説明します。
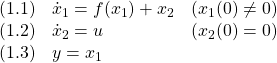
ここで、(1.1)が非線形動作を、(1.2)がアクチュエータ動作を、(1.3)が観測式を表しています。したがって、制御対象は状態変数![]() をもつ2次元の非線形系です。
をもつ2次元の非線形系です。
制御目的は状態変数![]() を速やかに零(平衡状態)に戻すこととします。
を速やかに零(平衡状態)に戻すこととします。
状態変数は![]() の2つなので、BS制御系設計のために2回の変数変換を行います。
の2つなので、BS制御系設計のために2回の変数変換を行います。

以下では、変数変換後の状態変数![]() について2次安定性(したがって漸近安定性)を示し、逆変換により、元の状態変数
について2次安定性(したがって漸近安定性)を示し、逆変換により、元の状態変数![]() についての漸近安定性を示します。
についての漸近安定性を示します。
●Step 1
まず第1番目の変数変換として、次を考えます。
![]()
また![]() に対する仮想的な操作変数
に対する仮想的な操作変数![]() を導入して、第2番目の変数変換
を導入して、第2番目の変数変換
![]()
を考えます。このとき(1.1)は次式で表されます。
![]()
このフィードバック線形化を行うために
![]()
と定義すると、![]() の状態方程式として
の状態方程式として
![]()
を得ます。これに対するリャプノフ関数
![]()
に対して、次式を得ます。
![]()
●Step 2
![]() の状態方程式として、(1.2)を用いて
の状態方程式として、(1.2)を用いて
![]()
を得ます。これに対するリャプノフ関数を
![]()
と定義すると、次式を得ます。
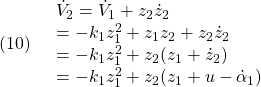
ここで、操作入力を
![]()
と選ぶと次式を得ます。
![]()
●以上の変数変換とその逆変換は、次式のように表すことができます。
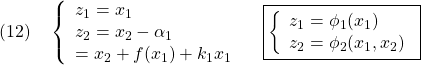
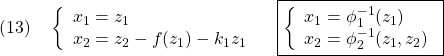
変数変換後の閉ループ系は次式で表されます。
![]()
すなわち
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \underbrace{ \left[\begin{array}{l} \dot{z}_1\\ \dot{z}_2 \end{array}\right]}_{\dot z}=- \underbrace{ \left[\begin{array}{cc} k_1 & 0\\ 0 & k_2 \end{array}\right]}_{K} \underbrace{ \left[\begin{array}{l} z_1\\ z_2 \end{array}\right]}_{z}+ \underbrace{ \left[\begin{array}{cc} 0 & 1\\ -1 & 0 \end{array}\right]}_{S} \underbrace{ \left[\begin{array}{l} z_1\\ z_2 \end{array}\right]}_{z} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5ba0b9891c7ccb17dde0e6f7efa61211_l3.png)
このとき、2次安定性
![]()
が示されており
![]()
が成り立ち、(13)から制御目的が達成されていることが分かります。
●フィードバック線形化(5)の実施においては、非線形関数![]() を正確にモデリングしておく必要がありますが、実際にはこれは一般には困難です。たとえば次の例を考えます。
を正確にモデリングしておく必要がありますが、実際にはこれは一般には困難です。たとえば次の例を考えます。
![]()
ここで、![]() は未知とします。第1項と第3項は線形の減衰項とみなせますが、第2項は非線形の減衰力で打ち消す必要があります。たとえば、
は未知とします。第1項と第3項は線形の減衰項とみなせますが、第2項は非線形の減衰力で打ち消す必要があります。たとえば、![]() に注意して
に注意して
![]()
と選ぶとき、次式が成り立ちます。
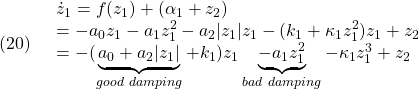
このとき、(6)の下で、次式を得ます。
![]()
また、(9)の下で
![]()
ここで、(11)のように![]() と選択すると
と選択すると
![]()
ここで、恒等式
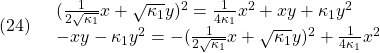
において、![]() とおけば、次式を得ます。
とおけば、次式を得ます。
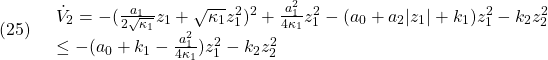
したがって、![]() と選べば、
と選べば、![]() を達成できます。すなわち、制御則(19)と(11)は、未知の
を達成できます。すなわち、制御則(19)と(11)は、未知の![]() を使わないので、BS制御はロバストであると言えます。
を使わないので、BS制御はロバストであると言えます。
Mass-Damper-Spring System
次のMDS(マス・ダンパ・バネ)系を考えます。
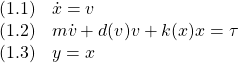
ここで、![]() は位置を、
は位置を、![]() は速度を、
は速度を、![]() は質量を、
は質量を、![]() は非線形の減衰係数を、
は非線形の減衰係数を、![]() は非線形のバネ係数を表しています。(1.1)と(1.2)が状態変数
は非線形のバネ係数を表しています。(1.1)と(1.2)が状態変数![]() をもつ非線形状態方程式、(1.3)が観測方程式です。
をもつ非線形状態方程式、(1.3)が観測方程式です。
制御目的は、目標軌道![]() に対する追従誤差
に対する追従誤差
![]()
を速やかに零とし目標軌道に乗せることです。基礎式は次のようにまとめられます。
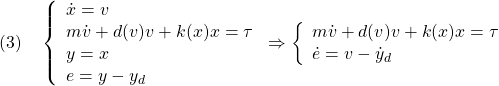
ここで、第1式が非線形動作を、第2式が追従誤差の振舞い(積分動作とは異なる)を表しています。
状態変数は![]() 、
、![]() の2つなので、BS制御系設計のために2回の変数変換を行います。
の2つなので、BS制御系設計のために2回の変数変換を行います。

以下では、変数変換後の状態変数![]() について2次安定性(したがって漸近安定性)を示し、逆変換により、元の状態変数
について2次安定性(したがって漸近安定性)を示し、逆変換により、元の状態変数![]() についての漸近安定性を示します。
についての漸近安定性を示します。
●Step 1
まず第1番目の変数変換として、次式を考えます。
![]()
![]() に対する仮想的な操作変数
に対する仮想的な操作変数![]() を導入して、第2番目の変数変換
を導入して、第2番目の変数変換
![]()
を考えます。このとき![]() の状態方程式
の状態方程式
![]()
を得ます。このフィードバック線形化を行うために
![]()
と定義すると、次式を得ます。
![]()
これに対するリャプノフ関数
![]()
に対して、次式を得ます。
![]()
●Step 2
![]() の状態方程式として、(5)から
の状態方程式として、(5)から
![]()
(3)を用いて次式を得ます。
![]()
これに対するリャプノフ関数を
![]()
と定義すると、次式を得ます。
![]()
ここで、操作入力を
![]()
と選ぶと次式を得ます。
![]()
●以上の変数変換とその逆変換は、次式のように表すことができます。
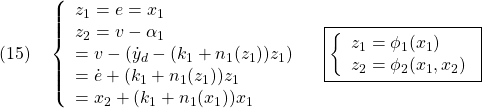
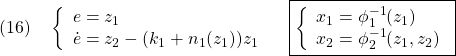
変数変換後の閉ループ系は次式で表されます。
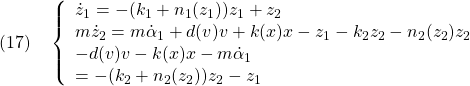
すなわち
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc} 1 & 0\\ 0 & m \end{array}\right]}_{M} \underbrace{ \left[\begin{array}{l} \dot{z}_1\\ \dot{z}_2 \end{array}\right]}_{\dot z}=- \underbrace{ \left[\begin{array}{cc} k_1+n_1(z_1) & 0\\ 0 & k_2+n_2(z_2) \end{array}\right]}_{K} \underbrace{ \left[\begin{array}{l} z_1\\ z_2 \end{array}\right]}_{z}\\ + \underbrace{ \left[\begin{array}{cc} 0 & 1\\ -1 & 0 \end{array}\right]}_{S} \underbrace{ \left[\begin{array}{l} z_1\\ z_2 \end{array}\right]}_{z} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7e30d4583990442c75248537bb56d2b1_l3.png)
このとき、2次安定性
![]()
が示されており
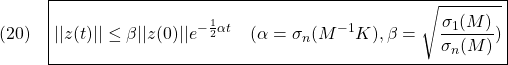
が成り立ち、制御目的が達成されていることが分かります。
●平衡状態の安定化問題は、次のように目標軌道が一定の特別な場合と考えられます。
![]()
簡単のため、![]() 、
、![]() とすると
とすると
![]()
となり、次式を得ます。
![]()
これは、次のような非線形のPD制御とみなすことができます。
![]()
実際、(4)より![]() 、
、![]() 、(5)より
、(5)より![]() に注意して
に注意して
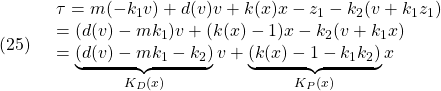
以下では積分動作を導入するための2つのアプローチを示します。
Integrator Augmentation
外乱の影響を受ける次のMDS(マス・ダンパ・バネ)系を考えます。
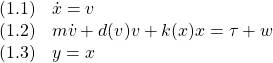
ここで、![]() は外乱を表しています。
は外乱を表しています。
制御目的は、外乱に抗して、目標軌道![]() に対する追従誤差
に対する追従誤差
![]()
を速やかに零とし目標軌道に乗せることです。
積分動作を入れて状態方程式を拡大した基礎式は次のようにまとめられます。
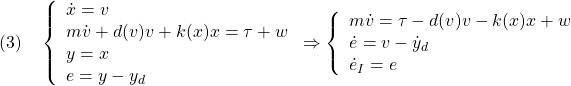
ここで、第1式が非線形動作を、第2式が追従誤差の振舞いを、第3式が積分動作を表しています。
状態変数は![]() 、
、![]() 、
、![]() の3つなので、BS制御系設計のために3回の変数変換を行います。
の3つなので、BS制御系設計のために3回の変数変換を行います。

以下では、変数変換後の状態変数![]() について2次安定性(したがって漸近安定性)を示し、逆変換により、元の状態変数
について2次安定性(したがって漸近安定性)を示し、逆変換により、元の状態変数![]() についての漸近安定性を示します。
についての漸近安定性を示します。
●Step 1
まず第1番目の変数変換として、次式を考えます。
![]()
![]() に対する仮想的な操作変数
に対する仮想的な操作変数![]() を導入して、第2番目の変数変換
を導入して、第2番目の変数変換
![]()
を考えます。このとき![]() の状態方程式
の状態方程式
![]()
を得ます。いま
![]()
と定義すると
![]()
これに対するリャプノフ関数
![]()
に対して、次式を得ます。
![]()
●Step 2
![]() の状態方程式として、(5)から
の状態方程式として、(5)から
![]()
![]() に対する仮想的な操作変数
に対する仮想的な操作変数![]() を導入して、第3番目の変数変換
を導入して、第3番目の変数変換
![]()
を考えます。このとき![]() の状態方程式
の状態方程式
![]()
を得ます。これに対するリャプノフ関数を
![]()
と定義すると、次式を得ます。
![]()
ここで
![]()
と定義すると、次式を得ます。
![]()
これから、次式を得ます。
![]()
●Step 3
![]() の状態方程式として、(11)から
の状態方程式として、(11)から
![]()
を得ます。このとき
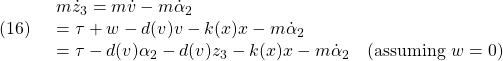
これに対するリャプノフ関数
![]()
に対して、次式を得ます。
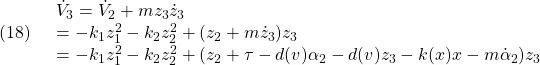
ここで、操作入力を
![]()
と選ぶと、次式を得ます。
![]()
●以上の変数変換とその逆変換は、次式のように表すことができます。
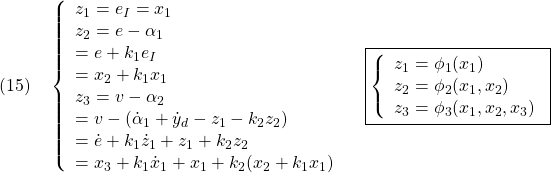
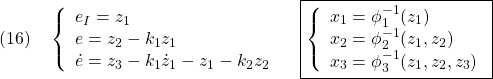
閉ループ系は次式で表されます。
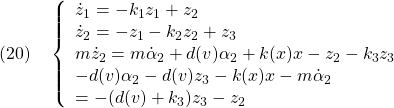
すなわち
![Rendered by QuickLaTeX.com \displaystyle{(21)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & m \end{array}\right]}_{M} \underbrace{ \left[\begin{array}{l} \dot{z}_1\\ \dot{z}_2\\ \dot{z}_3 \end{array}\right]}_{\dot z}=- \underbrace{ \left[\begin{array}{ccc} k_1 & 0 & 0\\ 0 & k_2 & 0\\ 0 & 0 & d(v)+k_3 \end{array}\right]}_{K} \underbrace{ \left[\begin{array}{l} z_1\\ z_2\\ z_3 \end{array}\right]}_{z}\\+ \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0\\ -1 & 0 & 1\\ 0 & -1 & 0 \end{array}\right]}_{S} \underbrace{ \left[\begin{array}{l} z_1\\ z_2\\ z_3 \end{array}\right]}_{z} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e4c27a02e87a8a58ef7fe31f40061a45_l3.png)
このとき、2次安定性
![]()
が示されており
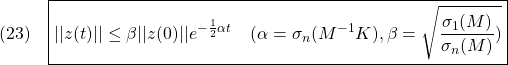
が成り立ち、制御目的が達成されていることが分かります。
Integral Action by Constant Parameter Adaptation
次の定値外乱の影響を受けるMDS(マス・ダンパ・バネ)系を考えます。
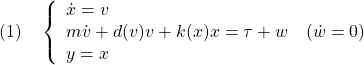
ここで、![]() は位置を、
は位置を、![]() は速度を、
は速度を、![]() は定値外乱を、
は定値外乱を、![]() は質量を、
は質量を、![]() は非線形の減衰係数を、
は非線形の減衰係数を、![]() は非線形のバネ係数を表しています。
は非線形のバネ係数を表しています。
制御目的は、定値外乱に抗して、目標軌道![]() に対する追従誤差
に対する追従誤差
![]()
を速やかに零とし目標軌道に乗せることです。基礎式は次のようにまとめられます。
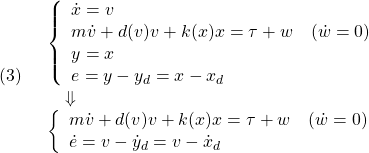
ここで、第1式が定値外乱下の非線形動作を、第2式が追従誤差の振舞いを表しています。
●Step 1
まず第1番目の変数変換として、次式を考えます。
![]()
![]() に対する仮想的な操作変数
に対する仮想的な操作変数![]() を導入して、第2番目の変数変換
を導入して、第2番目の変数変換
![]()
を考えます。このとき![]() の状態方程式
の状態方程式
![]()
を得ます。このフィードバック線形化を行うために
![]()
と定義すると、次式を得ます。
![]()
これに対するリャプノフ関数
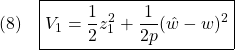
に対して、次式を得ます。
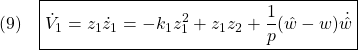
●Step 2
![]() の状態方程式として、(5)と(7)から
の状態方程式として、(5)と(7)から
![]()
よって、(3)から次式を得ます。
![]()
これに対するリャプノフ関数を
![]()
と定義すると、次式を得ます。
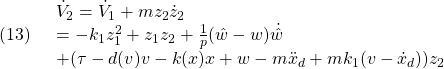
ここで、操作入力を
![]()
と選ぶと次式を得ます。
![]()
ここで、外乱の予測式を
![]()
と選べばよいことが分かります。
●閉ループ系は次式で表されます。
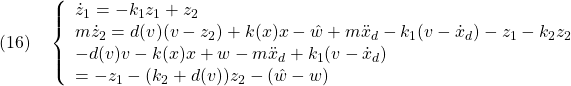
すなわち
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad \underbrace{ \left[\begin{array}{cc} 1 & 0\\ 0 & m \end{array}\right]}_{M} \underbrace{ \left[\begin{array}{l} \dot{z}_1\\ \dot{z}_2 \end{array}\right]}_{\dot z}=- \underbrace{ \left[\begin{array}{cc} k_1 & 1\\ -1 & -k_2-d(v) \end{array}\right]}_{A} \underbrace{ \left[\begin{array}{l} z_1\\ z_2 \end{array}\right]}_{z}+ \underbrace{ \left[\begin{array}{c} 0 \\ -1 \end{array}\right]}_{b} (\hat{w}-w) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-da7a835f971ce5dac2d1a21c12164a35_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \dot{\hat{w}}=-p \underbrace{ \left[\begin{array}{cc} 0 & -1 \end{array}\right]}_{b^T} \underbrace{ \left[\begin{array}{l} z_1\\ z_2 \end{array}\right]}_{z} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c15da6d97348e4f96dbe7ef9aee6bada_l3.png)