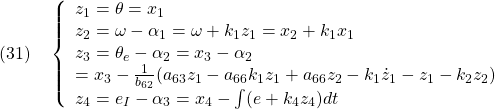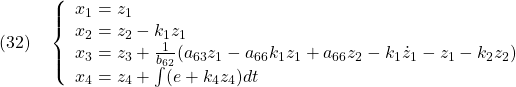Case1:3次元モデルに基づくBS制御
●制御対象YMCPBのピッチに関する運動方程式として次式を考えます。
![]()
これは次の形をとると考えられます。
![]()
ここで、減衰係数![]() 、復元係数
、復元係数![]() は、
は、![]() 、
、![]() の非線形関数、
の非線形関数、![]() は外乱やモデル化誤差を表しています。また、
は外乱やモデル化誤差を表しています。また、![]() は船外機の取付角で、その動作は操作変数
は船外機の取付角で、その動作は操作変数![]() を用いて、次式で表されます。
を用いて、次式で表されます。
![]()
(2)と(3)を合わせた制御対象全体の非線形状態方程式を線形化すると次式となります。
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \underbrace{ \frac{d}{dt} \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0\\ a_{63} & a_{66} & b_{62}\\ 0 & 0 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{cc} 0 \\ 0 \\ \Omega_e \end{array}\right] }_{B} u_e(t)\\ +\underbrace{ \left[\begin{array}{cccc} 0 & 0 & 0 & 0 \\ a_{62} & a_{64} & a_{65} & b_{61}\\ 0 & 0 & 0 & 0 \end{array}\right] \left[\begin{array}{c} z(t)-z^*\\ \dot{x}(t)-V^*\\ \dot{z}(t)\\ T(t)-T^* \end{array}\right] }_{w(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-44d46ce48189bf941958132e5f951657_l3.png)
ここで、![]() は平衡状態を表しています。
は平衡状態を表しています。
●以上から、制御対象は次式でモデル化されているとします。
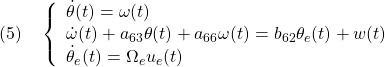
制御目的は、まず船外機の取付角を![]() に移動させること、その上で外乱に抗して船体のピッチ角の振動を抑え、平衡状態を保持することです。そのために、制御則には誤差
に移動させること、その上で外乱に抗して船体のピッチ角の振動を抑え、平衡状態を保持することです。そのために、制御則には誤差
![]()
による積分動作
![]()
を入れます。積分動作を入れて拡大した基礎式は次のようにまとめられます。
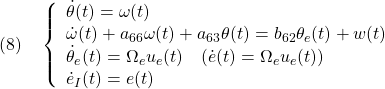
ここで、第1式と第2式が非線形動作を、第3式がアクチュエータの動作を、第4式が積分動作を表しています。以下では、簡単のため![]() とします。
とします。
状態変数は![]() 、
、![]() 、
、![]() 、
、![]() の4つなので、BS制御系設計のために4回の変数変換を行います。
の4つなので、BS制御系設計のために4回の変数変換を行います。
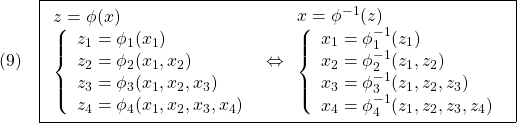
以下では、変数変換後の状態変数![]() について2次安定性(したがって漸近安定性)を示し、逆変換により、元の状態変数
について2次安定性(したがって漸近安定性)を示し、逆変換により、元の状態変数![]() についての漸近安定性を示します。
についての漸近安定性を示します。
●Step 1
まず第1番目の変数変換として、次式を考えます。
![]()
また![]() に対する仮想的な操作変数
に対する仮想的な操作変数![]() を導入して、第2番目の変数変換
を導入して、第2番目の変数変換
![]()
を考えます。このとき![]() の状態方程式は
の状態方程式は
![]()
となります。いま
![]()
と定義すると
![]()
となります。これに対するリャプノフ関数
![]()
に対して、次式を得ます。
![]()
●Step 2
![]() に対して仮想的な操作変数
に対して仮想的な操作変数![]() を導入して、第3番目の変数変換
を導入して、第3番目の変数変換
![]()
を考えます。このとき![]() の状態方程式として
の状態方程式として
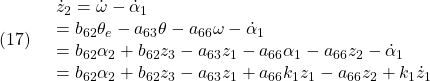
を得ます。このフィードバック線形化を行うために
![]()
と定義すると、次式を得ます。
![]()
これに対するリャプノフ関数を
![]()
と定義すると、次式を得ます。
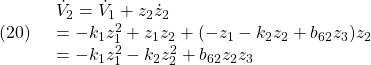
●Step 3
![]() の状態方程式として
の状態方程式として
![]()
このフィードバック線形化を行うために
![]()
と定義すると、次式を得ます。
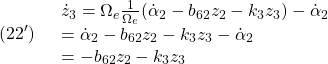
これに対するリャプノフ関数
![]()
に対して、次式を得ます。
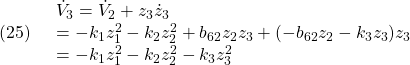
●Step 4
![]() に対して仮想的な操作変数
に対して仮想的な操作変数![]() を導入して、第4番目の変数変換
を導入して、第4番目の変数変換
![]()
を考えます。![]() の状態方程式は
の状態方程式は
![]()
いま
![]()
と定義すると
![]()
これに対するリャプノフ関数
![]()
に対して、次式を得ます。
![]()
●以上の変数変換とその逆変換は、次式のように表すことができます。