ここでは、 LQI制御に倣って積分動作をもつスライディングモード制御(SMI2制御)系の設計について述べます。その評価は本来は非線形シミュレータ上で行うべきですが、ここでは6次元線形モデルに関して行います。
| Case | 設計モデル | 状態FB | 状態OB | 積分動作 | 注意点 |
| 1 | 5次 | 5次 | 未使用 | 要 | 「絵に描いた餅」 |
| 2 | 5次 | 3次 | 不要 | 要 | ヒーブのゲインを強制的に零 |
| 3 | 3次 | 3次 | 不要 | 要 | ヒーブからの連成を抑制できるか |
| 4 | 5次 | 5次 | 要 | 要 | コントローラが微分方程式 |
Case1:5次元モデルに基づくSMI制御
●LQI制御における偏差系(7)を、改めて次のように書きます。
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot{x}_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} + \underbrace{ \left[\begin{array}{c} 0\\ I_m \end{array}\right] }_{B_{E3}} {\dot u}(t)\\ (x_1(t)=x(t)-x_\infty, x_2(t)=u(t)-u_\infty) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-287cdcd8e65d74ee36ec3b14429778da_l3.png)
スイッチング関数として、次式を考えます。
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} \ (M=S_2^{-1}S_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b29dc4a454912e8d6acde0686487f72b_l3.png)
(1)に対して、座標変換
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ -S_2^{-1}S_1 & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1d43b39400a0f9614aa7f3662f3f8fc4_l3.png)
を行って、次式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{x}'_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ \bar{A}_{21} & \bar{A}_{22} \\ \end{array}\right] }_{T_sA_{E3}T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} + \underbrace{ \left[\begin{array}{cc} 0\\ S_2 \end{array}\right] }_{T_sB_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ad4d0f30544fe9138bf4a06f0bbc0d3c_l3.png)
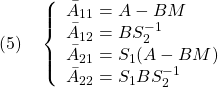
以下では、![]() が安定行列となるようにスイッチング関数が選ばれていると仮定します。
が安定行列となるようにスイッチング関数が選ばれていると仮定します。
●偏差系E3に対するSM制御は次式で与えられます。
![]()
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad {\dot u}_\ell(t)=-\underbrace{(SB_{E3})^{-1}(SA_{E3}-\Phi S)}_{K_{E3}=\left[\begin{array}{cc} K_1 & K_2 \end{array}\right]}}x_{E3}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-aa75a3fae556ffb1e063a6c3165e9f14_l3.png)
![]()
ここで、![]() は安定行列、
は安定行列、![]() は
は![]() の解です。
の解です。
これらを積分して、制御対象に対する積分動作をもつSM制御(SMI制御)を導出します。
![]()
まず(7)は次式のように書けます。
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad {\dot u}_\ell(t)=- \boxed{\underbrace{ (SB_{E3})^{-1}(SA_{E3}-\Phi S)S_E^{-1} }_{\left[\begin{array}{cc} F & F_I \end{array}\right]}} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-17dcffd80184d45c409aa1d4e2fd454e_l3.png)
これを積分して
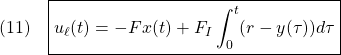
次に(8)は次式のように書けます。
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad {\dot u}_n(t) =-(SB_{E3})^{-1}\rho\, {\rm sgn}( \boxed{\underbrace{ P_2SS_E^{-1} }_{\left[\begin{array}{cc} G & G_I \end{array}\right]}} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)}) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-863369c4b058cffb357ac9501fed0507_l3.png)
これを積分すれば
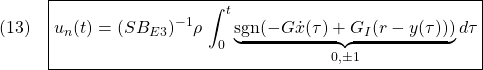
●制御対象YMCPBに対するSMI制御系を設計するプログラムを次に示します。
| MATLAB |
|
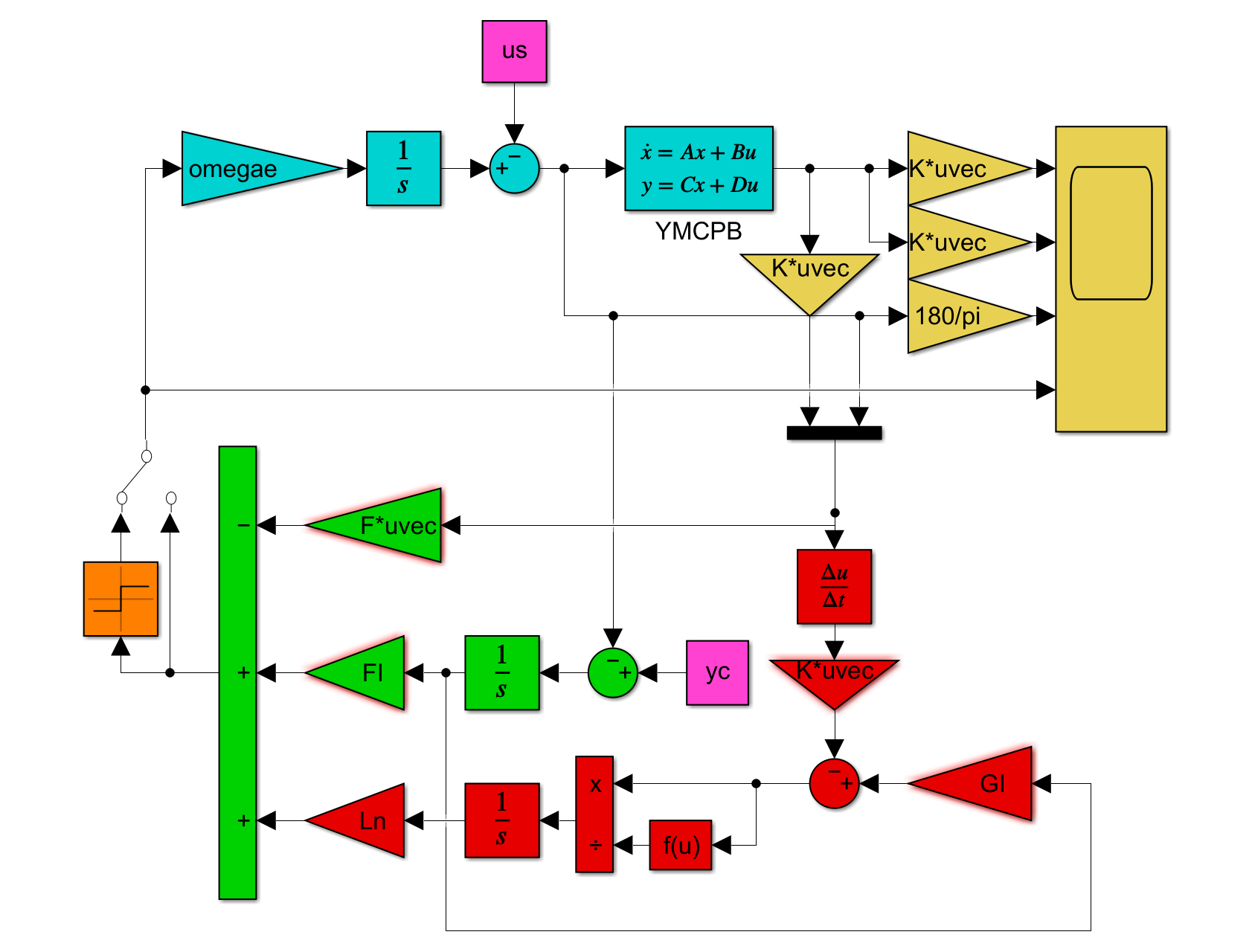
図1 SMI2制御系シミュレーション
これを実行して次のシミュレーション結果を得ます。
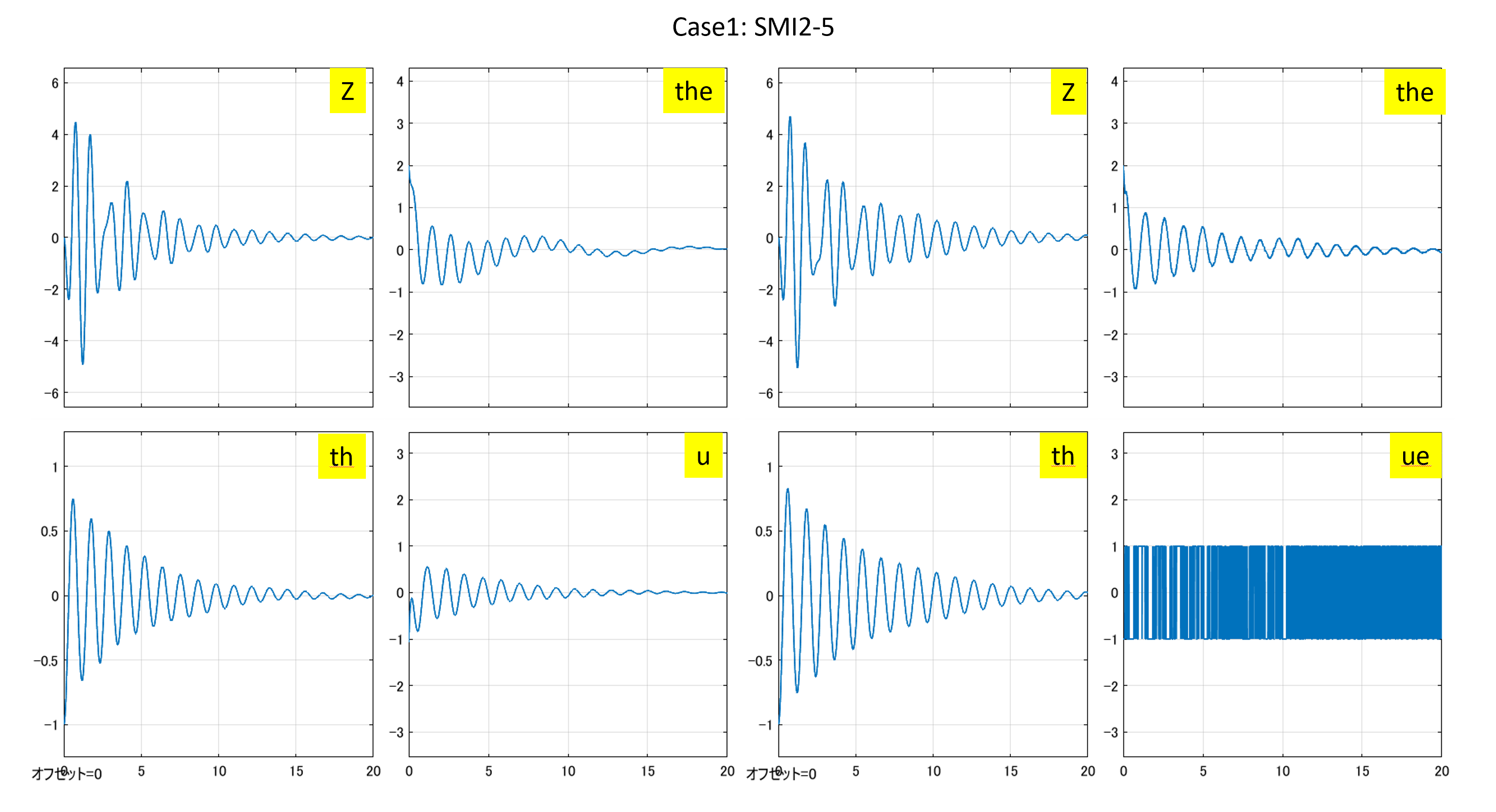
図2 5次元モデルに基づくSMI2制御系と符号関数を通したSMI制御
Case1’:Case1でヒーブゲインを零とする場合
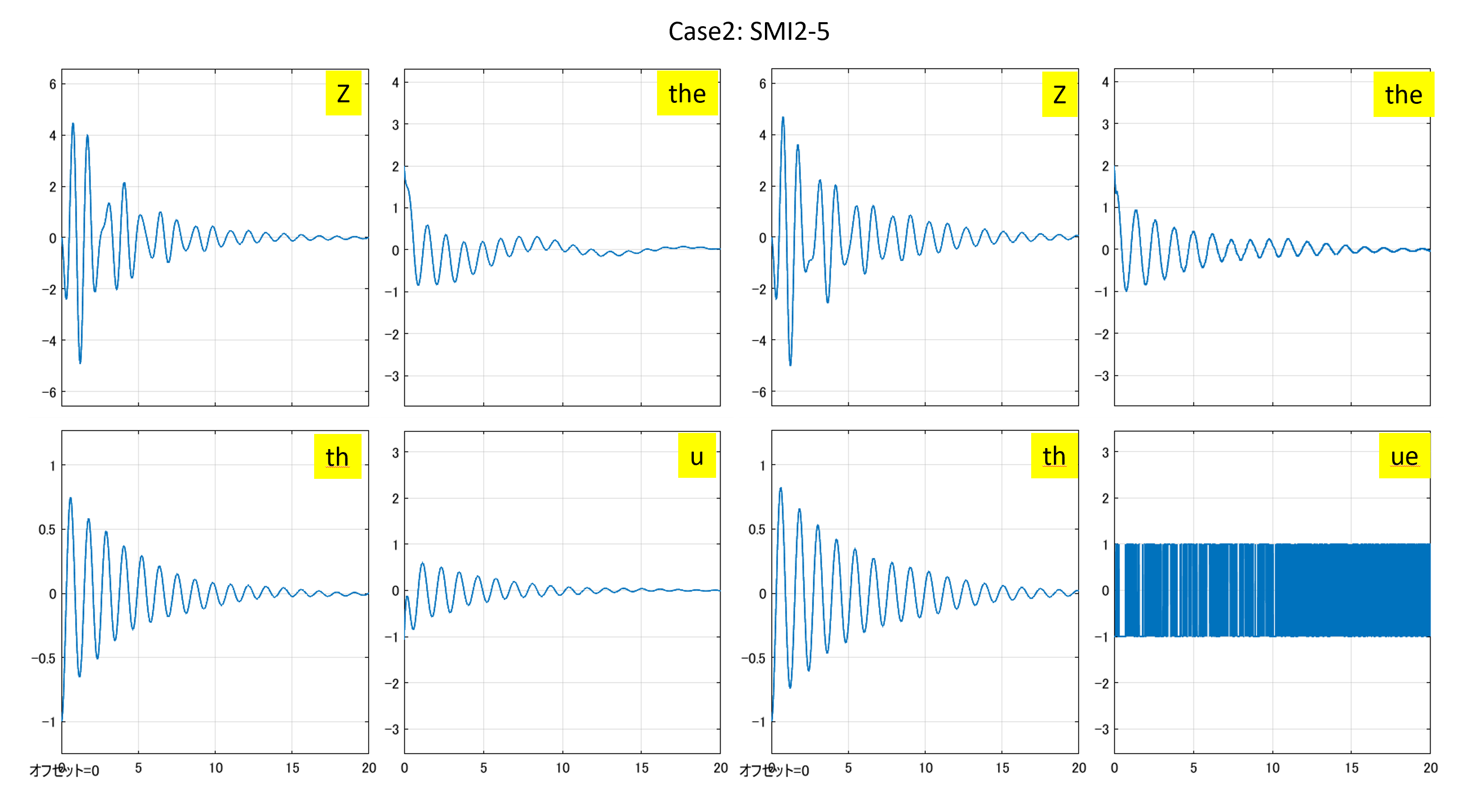
図3 ヒーブゲインを零とした場合のSMI2制御系と符号関数を通したSMI制御
Case2:3次元モデルに基づくSMI制御
●制御対象YMCPBに対するSMI制御系を設計するプログラムを次に示します。
| MATLAB |
|
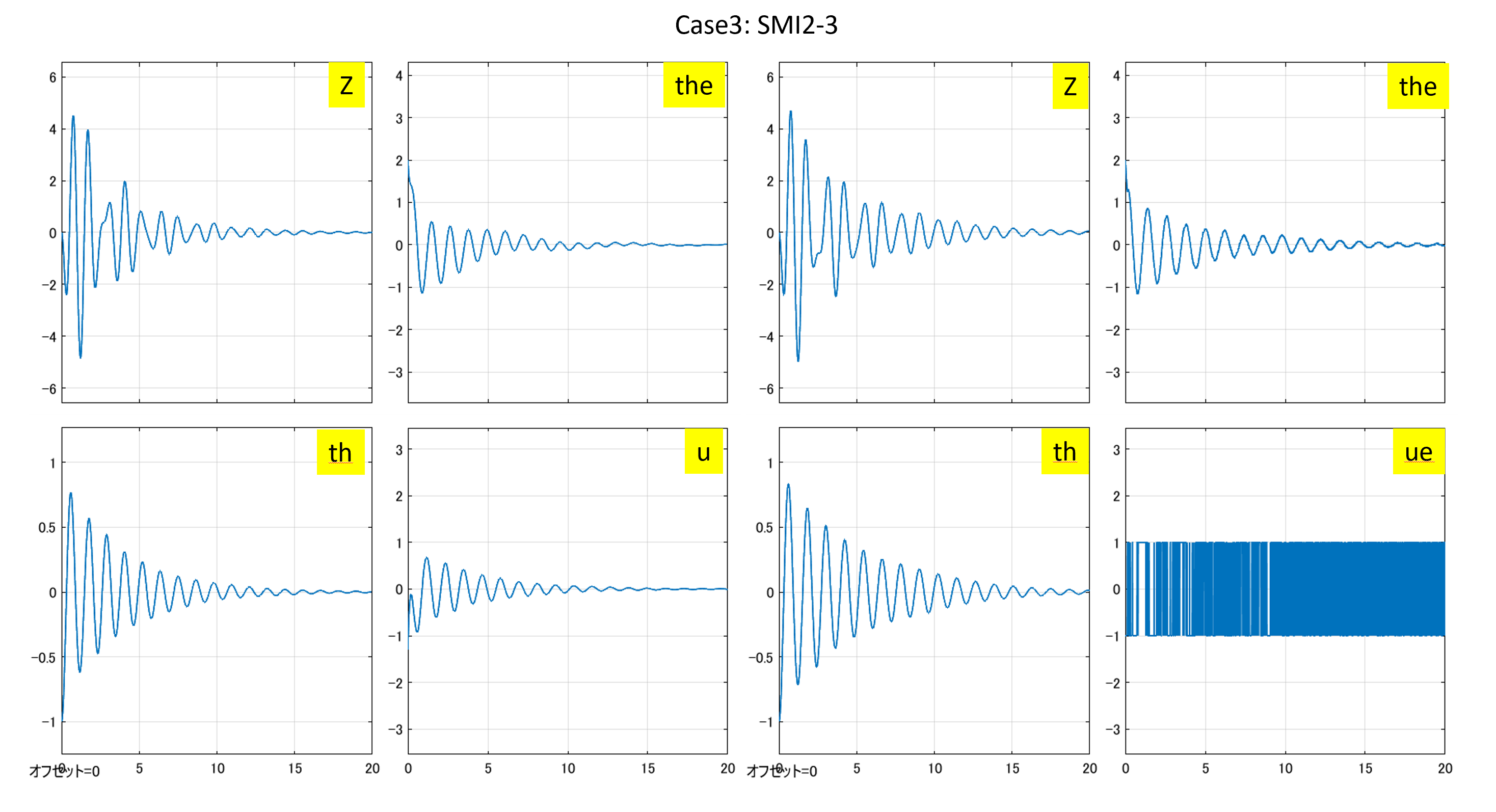
図4 3次元モデルに基づくSMI2制御系と符号関数を通したSMI2制御