SMオブザーバ
[1] 制御対象の状態空間表現として次式を考えます。
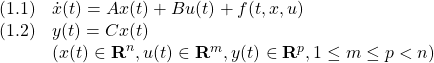
ただし、![]() はモデル誤差、非線形要素、外乱などの影響を表し、次のマッチング条件を満たすとします。
はモデル誤差、非線形要素、外乱などの影響を表し、次のマッチング条件を満たすとします。
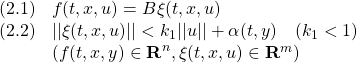
さらに次の3つを仮定します。
仮定![]()
![]() は可制御対
は可制御対
仮定![]()
![]() (相対次数1)
(相対次数1)
仮定![]()
![]() の不変零点は安定(最小位相系)
の不変零点は安定(最小位相系)
一般性を失うことなく、(1)は次のSM標準形であるとします。
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{ll} (3.1) & \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u(t)\\ (3.2) & y(t) = \underbrace{ \left[\begin{array}{cc} C_1 & C_2 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6ec74dc0c4572a9c7fa91295a5ba283b_l3.png)
●これに対して、次のSMオブザーバを考えます。
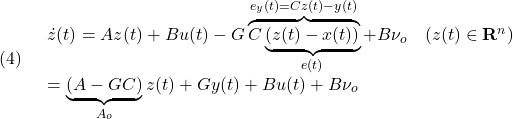
ここで、![]() は
は![]() が安定行列となるように選ばれているとします。また、
が安定行列となるように選ばれているとします。また、
![]()
を満足する![]() と、ある
と、ある![]() に対して
に対して
![]()
が満足されているものとします。このとき、![]() は
は
![]()
のように与えます。上の仮定![]() と
と![]() の下で、SMオブザーバの誤差は次の超平面上でスライディングモードを達成します。
の下で、SMオブザーバの誤差は次の超平面上でスライディングモードを達成します。
![]()
●以下では、![]() を仮定します。座標変換
を仮定します。座標変換
![]()
を行なうと
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{l} \underbrace{\left[\begin{array}{cc} {\cal A}_{11} & {\cal A}_{12}\\ {\cal A}_{21} & {\cal A}_{22} \end{array}\right]}_{{\cal A}}\\ =\underbrace{\left[\begin{array}{cc} {A}_{11}-{A}_{12}C_2^{-1}C_1 & A_{12}C_2^{-1} \\ C_1{\cal A}_{11}+C_2A_{21}-C_2A_{22}C_2^{-1}C_1 & C_1A_{12}C_2^{-1}+C_2A_{22}C_2^{-1} \end{array}\right] }_{T_cAT_c^{-1}}\\ {\cal B}=\underbrace{\left[\begin{array}{c} 0 \\ C_2B_2 \end{array}\right] }_{T_cB}\\ {\cal C}=\underbrace{\left[\begin{array}{cc} 0 & I_p \end{array}\right] }_{CT_c^{-1}}\\ {\cal P}= \underbrace{\left[\begin{array}{cc} I_{n-p} & 0 \\ -C_2^{-1}C_1 & C_2^{-1} \end{array}\right]^T \left[\begin{array}{cc} P_1 & 0\\ 0 & P_2 \end{array}\right] \left[\begin{array}{cc} I_{n-p} & 0 \\ -C_2^{-1}C_1 & C_2^{-1} \end{array}\right] }_{T_c^TPT_c}\\ =\left[\begin{array}{cc} I_{n-p} & -C_1^TC_2^{-T} \\ 0 & C_2^{-T} \end{array}\right]^T \left[\begin{array}{cc} P_1 & 0 \\ -P_2C_2^{-1}C_1 & P_2C_2^{-1} \end{array}\right]\\ =\left[\begin{array}{cc} P_1+C_1^TC_2^{-T}P_2C_2^{-1}C_1 & -C_1^TC_2^{-T}P_2C_2^{-1}\\ -C_2^{-T}P_2C_2^{-1}C_1 & C_2^{-T}P_2C_2^{-1} \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-23b25bc8ecbab40ee6e5976ebefccd82_l3.png)
を得ます。したがって
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} G=\underbrace{\left[\begin{array}{cc} I_{n-p} & 0 \\ -C_2^{-1}C_1 & C_2^{-1} \end{array}\right] }_{T_c^{-1}} \underbrace{\left[\begin{array}{c} A_{12}C_2^{-1}\\ C_1A_{12}C_2^{-1}+C_2A_{22}C_2^{-1}-{\cal A}_{22}^s \end{array}\right] }_{\left[\begin{array}{c} {\cal A}_{12}\\ {\cal A}_{22}-{\cal A}_{22}^s \end{array}\right]}\\ =\left[\begin{array}{c} A_{12}C_2^{-1} \\ A_{22}C_2^{-1}-C_2^{-1}A_{22}^S \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6f55e042f0e71a68f90ee8ddf5588d0c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \begin{array}{l} \underbrace{\left[\begin{array}{cc} P_1+C_1^TC_2^{-T}P_2C_2^{-1}C_1 & -C_1^TC_2^{-T}P_2C_2^{-1}\\ -C_2^{-T}P_2C_2^{-1}C_1 & C_2^{-T}P_2C_2^{-1} \end{array}\right] \left[\begin{array}{c} 0 \\ C_2B_2 \end{array}\right] }_{{\cal P}{\cal B}} = \underbrace{\left[\begin{array}{cc} 0 & I_p \end{array}\right]^T }_{{\cal C}^T} F^T\\ \Rightarrow F=(C_2^{-T}P_2C_2^{-1}C_2B_2)^T=B_2^TP_2C_2^{-1} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d8371d4e684ace7595130cce38802819_l3.png)
すなわち
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \boxed{\begin{array}{l} G= \left[\begin{array}{c} A_{12}C_2^{-1} \\ A_{22}C_2^{-1}-C_2^{-1}A_{22}^S \end{array}\right]\\ F=B_2^TP_2C_2^{-1} \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-acc6f79294b0cb173b67e46276765b51_l3.png)
ここまでの手順を、関数smobs3としてプログラムすることにします。
追従SMI制御
[2] 制御対象
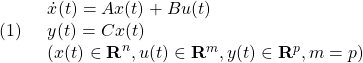
の出力を、コマンド(次式の解)
![]()
に追従させることを考えます(![]() は安定行列)。そのために、積分動作
は安定行列)。そのために、積分動作
![]()
を導入し、次の拡大系を構成します。ここで、(1)はすでに標準形であるとしています。
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \left[\begin{array}{c} \dot x_r(t)\\ \dot x(t) \end{array}\right] = \left[\begin{array}{c|cc} 0 & -C_1 & -C_2\\\hline 0 & A_{11} & A_{12} \\ 0 & A_{21} & A_{22} \end{array}\right] \left[\begin{array}{c} x_r(t)\\ x(t) \end{array}\right] + \left[\begin{array}{c} 0\\\hline 0\\ B_2 \end{array}\right] u(t) + \left[\begin{array}{c} I_m \\\hline 0 \\ 0 \end{array}\right] r(t)\\ (x_r(t)\in{\rm\bf R}^m, x(t)\in{\rm\bf R}^n) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1ab4b378422eddd1bff475a2408082e2_l3.png)
これを、次のように分割し直しても標準形であることには変わりありません。
![Rendered by QuickLaTeX.com \displaystyle{(5a)\quad \begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc|c} 0 & -C_1 & -C_2\\ 0 & A_{11} & A_{12} \\\hline 0 & A_{21} & A_{22} \end{array}\right] }_{\tilde{A}=\left[\begin{array}{cc} \tilde{A}_{11} & \tilde{A}_{12} \\ \tilde{A}_{21} & \tilde{A}_{22} \\ \end{array}\right]} \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0\\ 0\\\hline B_2 \end{array}\right] }_{\tilde{B}} u(t) + \left[\begin{array}{c} I_m \\ 0 \\\hline 0 \end{array}\right] r(t)\\ (x_1(t)\in{\rm\bf R}^n, x_2(t)\in{\rm\bf R}^m) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a01e5393ef83d3a307441de8778d577b_l3.png)
ただし
![]()
●この積分器による拡大系を安定化できれば、積分器の値![]() は定値となり、被積分項
は定値となり、被積分項![]() の値は零となり、
の値は零となり、![]() は
は![]() へ漸近します。そこで、SM制御によって拡大系を安定化し、追従制御系を構成することを考えます。この制御系は特別な
へ漸近します。そこで、SM制御によって拡大系を安定化し、追従制御系を構成することを考えます。この制御系は特別な![]() の場合を含みますので、まずスイッチング関数として、次式を考えます。
の場合を含みますので、まずスイッチング関数として、次式を考えます。
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} %\underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] %}_{x(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I_m \\ \end{array}\right] }_{S} %\underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] %}_{x(t)} \ (M=S_2^{-1}S_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-01bb686061b94fbab2a0ff90e7d23f64_l3.png)
(5)に対して、座標変換
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} I_n & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right]\\ \Leftrightarrow \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} I_n & 0 \\ -S_2^{-1}S_1 & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-19e5643bcb296d8a517aba35bc4fe14e_l3.png)
を行って、次式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(8a)\quad \begin{array}{l} %\underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] %}_{\dot{x}'(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ S_2\bar{A}_{21} & S_2\bar{A}_{22}S_2^{-1} \\ \end{array}\right] }_{T_sA_ET_s^{-1}} %\underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] %}_{x'(t)} + \underbrace{ \left[\begin{array}{cc} 0\\ S_2B_2 \end{array}\right] }_{T_sB_E} u(t)\\ + \left[\begin{array}{cc} B_r \\ S_1B_r \end{array}\right] r(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a23595fe93cd3fb99284c6e90f61bcf1_l3.png)
ただし
![Rendered by QuickLaTeX.com \displaystyle{(8b)\quad \left\{\begin{array}{l} \bar{A}_{11}=\underbrace{ \left[\begin{array}{cc} 0 & -C_1 \\ 0 & A_{11} \end{array}\right]}_{\tilde{A}_{11}} -\underbrace{\left[\begin{array}{c} -C_2\\ A_{12} \end{array}\right]}_{\tilde{A}_{12}}M\quad(M=S_2^{-1}S_1)\\ \bar{A}_{12}= \underbrace{\left[\begin{array}{c} -C_2\\ A_{12} \end{array}\right]}_{\tilde{A}_{12}}S_2^{-1}\\ \bar{A}_{21}=S_2(M\bar{A}_{11} + \left[\begin{array}{cc} 0 & A_{21} \end{array}\right] -A_{22}M)\\ \bar{A}_{22}=S_2(M \left[\begin{array}{c} -C_2\\ A_{12} \end{array}\right] +A_{22})S_2^{-1}\\ B_r=\left[\begin{array}{cc} I_m \\ 0 \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a8cb0e83576eef13d13b8f669a414ae8_l3.png)
ここで、![]() が安定行列となるように行列
が安定行列となるように行列![]() が選ばれているとします。
が選ばれているとします。
●特別な![]() の場合のスライディングモードは
の場合のスライディングモードは![]() で表されますが、一般の
で表されますが、一般の![]() の場合のスライディングモードは
の場合のスライディングモードは
![]()
で表されるとします。ここで、![]() の選び方についてはあとで述べます。
の選び方についてはあとで述べます。
●以上の準備の下で、制御則は次式で表されます。
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{l} u(t)=u_L(t)+\nu_c\\ u_L(t)=-\underbrace{(S\tilde{B})^{-1}(S\tilde{A}-\Phi S)}_{L=L_{eq}+L_\Phi}\left[\begin{array}{c} x_r(t)\\ x(t) \end{array}\right]\\ -\underbrace{(S\tilde{B})^{-1}(\Phi S_r+S_1B_r)}_{L_r} r(t) +\underbrace{(S\tilde{B})^{-1}S_r}_{L_{\dot r}} \dot{r}(t)\\ \nu_c=-\underbrace{(S\tilde{B})^{-1}\rho_c(u_L,y)}_{L_n}\frac{P_2(s(t)-S_rr(t))}{||P_2(s(t)-S_rr(t))||} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4fa5c5c72c2ee8614e09bcaa4631f9d9_l3.png)
これをSMオブザーバを用いて実施する場合は次式を用います(![]() )。
)。
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} \hat{u}(t)=\underbrace{-L\left[\begin{array}{c} x_r(t)\\ z(t) \end{array}\right]-L_rr(t)+L_{\dot r}\dot{r}(t)}_{\hat{u}_L}+\hat{\nu}_c\\ \displaystyle{\hat{\nu}_c=-L_n\frac{P_2(S\left[\begin{array}{c} x_r(t)\\ z(t) \end{array}\right]-S_rr(t))}{||P_2(S\left[\begin{array}{c} x_r(t)\\ z(t) \end{array}\right]-S_rr(t))||}}\\ L=\Lambda^{-1}(S\tilde{A}-\Phi S)\\ L_r=\Lambda^{-1}(\Phi S_r+S_2MB_r)\\ L_{\dot r}=\Lambda^{-1}S_r\\ L_n=\Lambda^{-1}\rho_c(\hat{u}_L,y) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9b9975d5d229ccc8642e2fdd4c1c0561_l3.png)
![]()
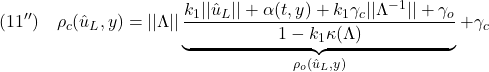
Note C91 ![]() の選び方
の選び方
●積分動作で示した閉ループ系の状態方程式の一部
![]()
を考えます。定常状態でスライディングモードが達成されたとすると
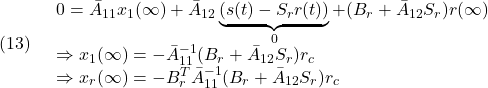
を得ます。![]() とするためには
とするためには
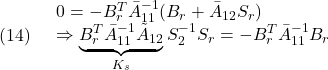
において、![]() が正則であれば、
が正則であれば、![]() を
を
![]()
と求めることができます。そこで次式に注目します。
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \begin{array}{l} \left[\begin{array}{cc} I & 0\\ B_r^T\tilde{A}_{11}^{-1} & -K_s \end{array}\right]= \left[\begin{array}{cc} \tilde{A}_{11} & \tilde{A}_{12}\\ B_r^T & 0 \end{array}\right] \left[\begin{array}{cc} \bar{A}_{11}^{-1} & -\bar{A}_{11}^{-1}\tilde{A}_{12}\\ 0 & I \end{array}\right]\\ = \left[\begin{array}{cc} \tilde{A}_{11} & \tilde{A}_{12}\\ B_r^T & 0 \end{array}\right] \left[\begin{array}{cc} I & 0\\ -M & I \end{array}\right] \left[\begin{array}{cc} \bar{A}_{11}^{-1} & -\bar{A}_{11}^{-1}\tilde{A}_{12}\\ 0 & I \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-359f0d62c20de545dd87152fb1c6a94b_l3.png)
これより![]() が正則であるための条件が次のように求められます。
が正則であるための条件が次のように求められます。
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \begin{array}{l} {\rm det}\left[\begin{array}{cc} \tilde{A}_{11} & \tilde{A}_{12}\\ B_r^T & 0 \end{array}\right]\ne 0 \Leftrightarrow {\rm det}\left[\begin{array}{cc|c} 0 & -C_1 & -C_2\\ 0 & A_{11} & A_{12}\\\hline I & 0 & 0 \end{array}\right]\ne 0\\ \Leftrightarrow {\rm det}\left[\begin{array}{cc} -C_1 & -C_2\\ A_{11} & A_{12} \end{array}\right]\ne 0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8d7129e0a72d941b228a1e4ecda1d741_l3.png)
これは不変零点が複素平面原点にはないことを意味しますが、仮定![]() により保証されており、
により保証されており、![]() の正則性が成り立ちます。
の正則性が成り立ちます。