| MATLAB |
%ex4_of_sm.m
%-----
clear all, close all
%(A,B,C)
A=[0 0 1 0 0;
0 -0.1540 -0.0042 1.5400 0;
0 0.2490 -1.0000 -5.2000 0;
0.0386 -0.9960 -0.0003 -0.1170 0;
0 0.5 0 0 -0.5];
pl=eig(A)
B=[0 0;
-0.7440 -0.0320;
0.3370 -1.1200;
0.0200 0;
0 0];
CM=[0 1 0 0 -1;
0 0 1 0 0;
0 0 0 1 0;
1 0 0 0 0];
C=[1 0 0 0 0;
0 0 0 1 0];
[nn,mm]=size(B);
[pp,nn]=size(CM);
%-----
% p1=[-0.05 -2 1.5 -1.5 1.5]
% p1=[-0.05 -2+1.5*i -2-1.5*i -1.5+1.5*i -1.5-1.5*i]
Lx=[-0.3131 3.3211 -0.1386 -0.7379 4.1180;
3.9524 5.6616 2.2906 -65.6425 -90.7262];
pCL=eig(A+B*Lx)
Am=A+B*Lx;
Lr=-inv(C*(Am\B));
Bm=B*Lr;
Cm=C;
%-----
[Af,Bf,Cf,r,Ta,Aa,Ba,Ca,Tb,T,Ac,Bc,Cc,Tc]=ca_form1(A,B,CM)
%-----
%Assumes the triple (A,B,C) is in the canonical form of Lemma 5.3
%p1 is an nn-pp-r vector containing the desired poles of (A22o+Lo A21o)
%p2 is an nn-mm-r vector containing the desired poles of (A11tilde-A122 K)
%p3 is an mm vector representing the poles of the range space dynamics
A11o=Af(1:r,1:r);
A12o=Af(1:r,r+1:nn-pp);
A22o=Af(r+1:nn-pp,r+1:nn-pp);
A21o=Af(nn-pp+1:nn-mm,r+1:nn-pp);
A121m=Af(1:r,nn-pp+1:nn-mm);
A122m=Af(r+1:nn-pp,nn-pp+1:nn-mm);
A22m=Af(nn-pp+1:nn-mm,nn-pp+1:nn-mm);
A121=Af(1:r,nn-mm+1:nn);
A122=Af(r+1:nn-mm,nn-mm+1:nn);
A211=Af(nn-mm+1:nn,1:r);
A212=Af(nn-mm+1:nn,r+1:nn-pp);
A213=Af(nn-mm+1:nn,nn-pp+1:nn-mm);
A22=Af(nn-mm+1:nn,nn-mm+1:nn);
A11tilde=[A22o A122m;A21o A22m];
A1221=A122(1:nn-pp-r,:);
A1222=A122(nn-pp-r+1:nn-mm-r,:);
%-----
p1=-5
Lo=place(A22o',-A21o',p1)
Lo=Lo';
%-----
Tr=Ta*Tb*Tc
Q=diag([5,1,1,5,5]);
Qt=Tr*Q*Tr';
Q11=Qt(1:nn-mm,1:nn-mm);
Q12=Qt(1:nn-mm,nn-mm+1:nn);
Q21=Qt(nn-mm+1:nn,1:nn-mm);
Q22=Qt(nn-mm+1:nn,nn-mm+1:nn);
Qhat=Q11-Q12*inv(Q22)*Q21;
Rhat=Q22;
[K,pl]=opt(A11tilde,A122,eye(3),Qhat,Rhat);
K1=K(:,1:nn-pp-r)
K2=K(:,nn-pp-r+1:nn-mm-r)
%-----
H=A22o+Lo*A21o
D1=A122m+Lo*A22m-H*Lo
D2=A1221+Lo*A1222
K=K2-K1*Lo
Kc=K1
Hhat=[A11o A12o;
zeros(nn-pp-r,r) H]
Dhat=[A121m-A12o*Lo A121;
D1 D2]*T'
%-----
S2=eye(mm);
S=S2*[zeros(mm,r) Kc K eye(mm)]
Ahat=[A11o A12o A121m-A12o*Lo A121;
zeros(nn-pp-r,r) H D1 D2;
zeros(pp-mm,r) A21o A22m-A21o*Lo A1222;
A211 A212 A213-A212*Lo A22]
p3=[-5,-5]
Phi=diag(p3)
Lambda=S*Bf
L=-inv(Lambda)*S*Ahat+inv(Lambda)*Phi*S
rho=1
Ln=rho*inv(Lambda)
P2=lyap(Phi',eye(mm))
%-----
%eof
|
![]()
![]()
![]()
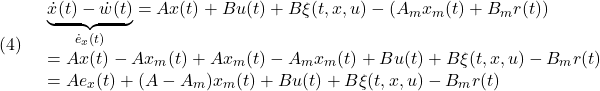
![]()
![]()
![]()
![]()
![]() を
を![]()
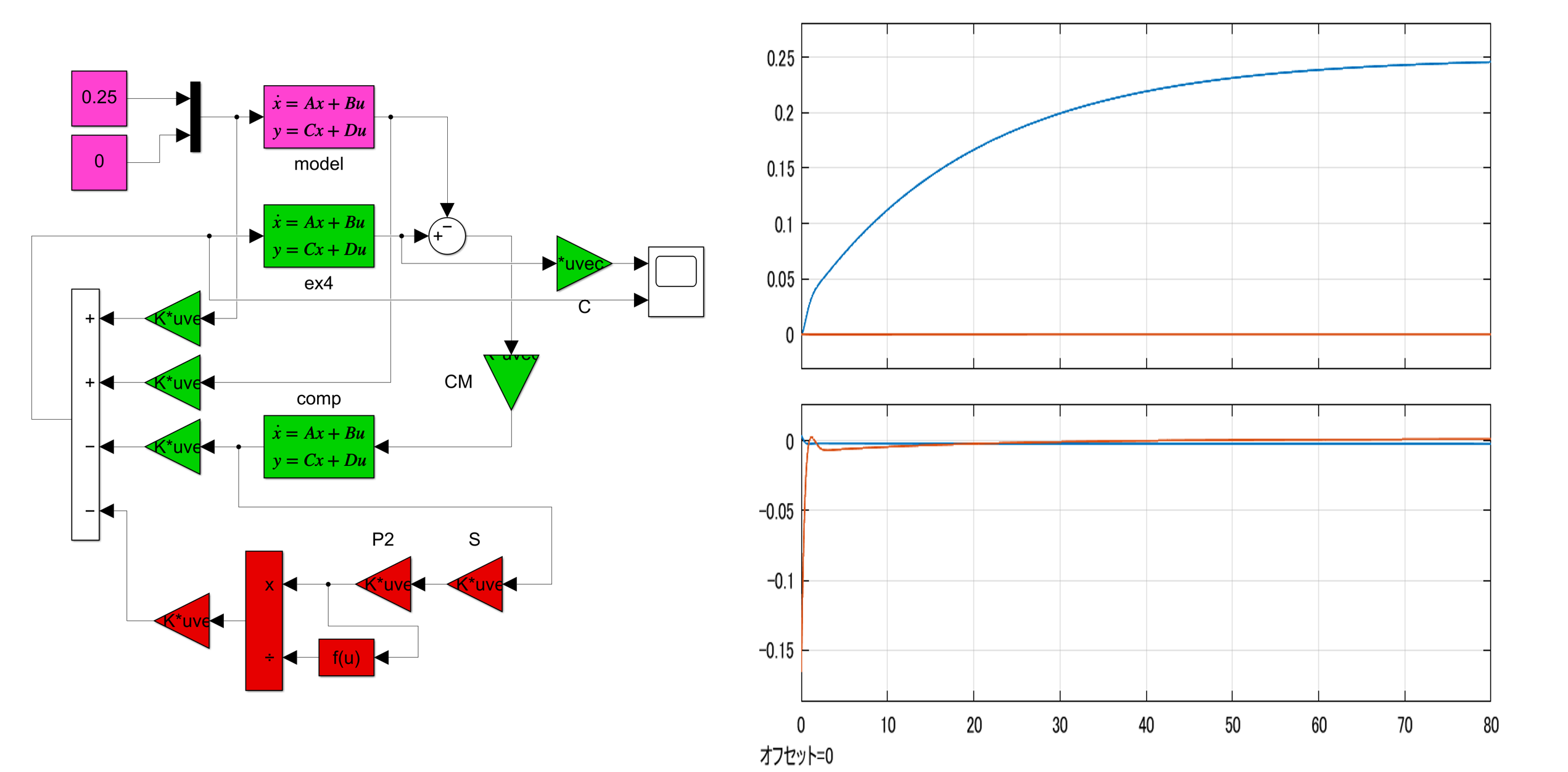
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} \dot{x}(t)=Ax(t)+Bu(t)\\ x(t)= \left[\begin{array}{ll} \phi & bank\ angle\\ r & yaw\ rate\\ p & roll\ rate\\ \beta & sideslip\ angle\\ x_5 & washed-out\ filter\ state \end{array}\right],\quad u(t)= \left[\begin{array}{ll} \delta_r & rudder\ deflection\\ \delta_a & aileron\ deflection \end{array}\right]\\ A=\left[\begin{array}{rrrrr} 0 & 0 & 1.0000 & 0 & 0\\ 0 & -0.1540 & -0.0042 & 1.5400 & 0\\ 0 & 0.2490 & -1.0000 & -5.2000 & 0\\ 0.0386 & -0.9960 & -0.0003 & -0.1170 & 0\\ 0 & 0.5000 & 0 & 0 & -0.5000 \end{array}\right],\quad\\ B=\left[\begin{array}{rr} 0 & 0 \\ -0.7440 & -0.0320 \\ 0.3370 & -1.1200 \\ 0.0200 & 0\\ 0 & 20 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8622180be357918528164e3d543e7c84_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \begin{array}{l} y(t)=C_Mx(t),\ z(t)=Cx(t)\\ y(t)= \left[\begin{array}{ll} r_{wo} & washed-out\ yaw\ rate\\ p & roll\ rate\\ \beta & sideslip\ angle\\ \phi & bank\ angle \end{array}\right],\quad z(t)= \left[\begin{array}{ll} \phi & bank\ angle\\ \beta & sideslip\ angle \end{array}\right]\\ C_M=\left[\begin{array}{rrrrr} 0 & 1 & 0 & 0 & -1\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 1 & 0 & 0 & 0 & 0 \end{array}\right],\quad C=\left[\begin{array}{rrrrr} 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a47cabffa6576dc1b9f48be4914a76a7_l3.png)
![]() 行列の固有値は次のように求められます。
行列の固有値は次のように求められます。