補遺:偏差系の安定化SM制御…Homework
レギュレータ問題は平衡状態の安定化、追値問題は他の平衡状態への安定化を意味します。LQI制御のところでみたように、偏差系を導入すれば、追値問題は偏差系の安定化問題となります。この観点から積分動作導入による追従SM制御を見直してみます。
[1] 定値外乱を受ける制御対象
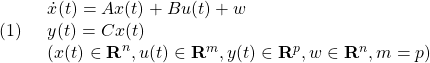
の出力を、次のコマンド(定値目標)
![]()
に追従させることを考えます。そのために、積分動作
![]()
を考え、次の拡大系を構成します。
![]()
定常状態では
![]()
を得ます(![]() ,
,![]() ,
,![]() は定数ベクトル)。まず、(4)から(5)を引いて、つぎの偏差系を得ます。
は定数ベクトル)。まず、(4)から(5)を引いて、つぎの偏差系を得ます。
偏差系E1:
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{c} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] }_{\dot{x}_{E1}(t)} = \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E1}} \underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] }_{x_{E1}(t)} + \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E1}} (u(t)-u_\infty) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-31c37a9934e5cdea3c7a11d0c5575b8d_l3.png)
この両辺を微分すれば、状態変数の中の定数ベクトルを除くことができて
偏差系E2:
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{\dot{x}_{E2}(t)} = \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E2}} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)} + \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E2}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3876d07fd5a0b32e63fa8f91e20b8ad7_l3.png)
を得ます。さらに、(1)の状態方程式と観測方程式をまとめた
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \left[\begin{array}{c} {\dot x}(t)-w \\ y(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S_E} \left[\begin{array}{c} x(t) \\ u(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-28a64d5f6becf5dc458bf65746e1d706_l3.png)
から、(5)すなわち
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \left[\begin{array}{c} -w \\ r \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S_E} \left[\begin{array}{c} x_\infty \\ u_\infty \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-70b5e47d55a371255ff67868bd470bbe_l3.png)
を引いて、つぎの関係式が成り立ちます。
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S_E} \underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d19845bc6a9ba5e6b6ffcc474aa170e5_l3.png)
これを用いて、偏差系E2に座標変換を行えば
偏差系E3:
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{\dot{x}_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} \underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e12324e6656148ca4b9a647055b6df5a_l3.png)
を得ます。ここで、つぎの関係式を用いました。
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E2}} \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S_E} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S_E} \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-790b5d3825c0777b3d3285e5fd6b1394_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E2}} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S_E} \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E3}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c15c3050bb3a9a40764927acc7268c81_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \underbrace{ \left[\begin{array}{cc} 0 & I_m \end{array}\right] }_{C_{E2}} \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S_E} = \underbrace{ \left[\begin{array}{cc} C & 0 \end{array}\right] }_{C_{E3}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fa6e5db5cb4e863339f8797520d1a2b2_l3.png)
以下では、この偏差系E3が標準形となっていることに注意して、SMCを設計します。
(11)を、改めて次のように書きます。
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot{x}_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} + \underbrace{ \left[\begin{array}{c} 0\\ I_m \end{array}\right] }_{B_{E3}} {\dot u}(t)\\ (x_1(t)=x(t)-x_\infty, x_2(t)=u(t)-u_\infty) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-245a3ce1c7bbd57f344bac4b6ccdca9c_l3.png)
スイッチング関数として、次式を考えます。
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} \ (M=S_2^{-1}S_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cdba45c2f46a4ded8109c4031c43eef8_l3.png)
(15)に対して、座標変換
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ -S_2^{-1}S_1 & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-272d89e0452752b99489c956de386a73_l3.png)
を行って、次式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{x}'_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ \bar{A}_{21} & \bar{A}_{22} \\ \end{array}\right] }_{T_sA_{E3}T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} + \underbrace{ \left[\begin{array}{cc} 0\\ S_2 \end{array}\right] }_{T_sB_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5ab2f4f17de6fee9605aa2556d7f248c_l3.png)
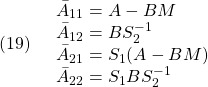
以下では、![]() が安定行列となるようにスイッチング関数が選ばれていると仮定します。
が安定行列となるようにスイッチング関数が選ばれていると仮定します。
このとき、スライディングモード制御則(SM制御則、SMC則)
![]()
を、2次安定性
![Rendered by QuickLaTeX.com \displaystyle{(21)\quad \begin{array}{lll} V(\bar{x})= \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]^T }_{\bar{x}^T(t)} \underbrace{ \left[\begin{array}{cc} P_1 & 0\\ 0 & P_2 \end{array}\right] }_{P} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)}\\ \Rightarrow \dot{V}(\bar{x})\le - \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]^T }_{\bar{x}^T(t)} \underbrace{ \left[\begin{array}{cc} Q_1 & 0\\ 0 & I \end{array}\right] }_{Q} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7c77aa3ff56d9793c30ad999001a2185_l3.png)
すなわち
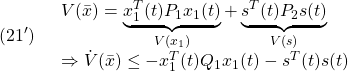
が成り立つように決定します(![]() ,
, ![]() ,
, ![]() )。
)。
[2] 可到達性の検討
等価制御は
![Rendered by QuickLaTeX.com \displaystyle{(22)\quad \begin{array}{l} s(t)=0\Rightarrow\dot{s}(t)=0 \Rightarrow 0=\bar{A}_{21}x_1(t)+\bar{A}_{22}s(t)+S_2{\dot u}(t)\\ \Rightarrow {\dot u}_{eq}(t)=-\underbrace{S_2^{-1}}_{(SB_{E3})^{-1}} \underbrace{\left[\begin{array}{cc} \bar{A}_{21} & \bar{A}_{22} \\ \end{array}\right]x'_{E3}(t)}_{SA_{E3}x_{E3}(t)}} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3ad4a24162e39c9dd7341a0db806bc67_l3.png)
のように得られます。(20)の第1項![]() は、この等価制御をベースして
は、この等価制御をベースして
![Rendered by QuickLaTeX.com \displaystyle{(23)\quad \begin{array}{l} {\dot u}_\ell(t)=-\underbrace{S_2^{-1}}_{(SB_{E3})^{-1}} \underbrace{(\left[\begin{array}{cc} \bar{A}_{21} & \bar{A}_{22} \\ \end{array}\right]x'_{E3}(t)-\Phi s(t))}_{(SA_{E3}-\Phi S)x_{E3}(t)}} \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4da62d9774c6809e24338ce1ff05a030_l3.png)
のように構成します(![]() は安定行列)。このとき閉ループ系は次式で与えられます。
は安定行列)。このとき閉ループ系は次式で与えられます。
![]()
すなわち
![]()
ここで、![]() は安定行列なので
は安定行列なので
![]()
を満たす![]() を選ぶことができます。これを用いて
を選ぶことができます。これを用いて
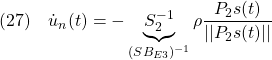
と選びます(![]() は定数)。このとき次式が成り立ちます。
は定数)。このとき次式が成り立ちます。
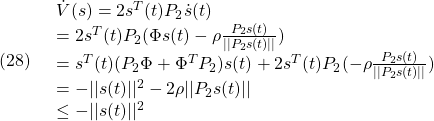
[3] スライディングモードの検討
![]() は安定行列なので
は安定行列なので
![]()
を満たす![]() を選ぶことができます。
を選ぶことができます。
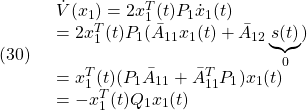
[4] 積分動作をもつSMC
上で求めた偏差系E3に対するSMCは次式で与えられました。
![]()
![]()
![]()
これらを積分して、制御対象(1)に対する積分動作をもつSMCを導出します。
![]()
まず(32)は(10)を用いて次式のように書けます。
![Rendered by QuickLaTeX.com \displaystyle{(35)\quad {\dot u}_\ell(t)=- \underbrace{ (SB_{E3})^{-1}(SA_{E3}-\Phi S)S_E^{-1} }_{\left[\begin{array}{cc} F & F_I \end{array}\right]} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-edb851ab679593bf698b480644ba82ce_l3.png)
これを積分して
![]()
次に(33)は(10)を用いて次式のように書けます。
![Rendered by QuickLaTeX.com \displaystyle{(37)\quad {\dot u}_n(t) =-S_2^{-1}\rho\, {\rm sgn}( \underbrace{ P_2SS_E^{-1} }_{\left[\begin{array}{cc} G & G_I \end{array}\right]} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)}) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-913747aecf41d0c7b9c2a72e8ab5d520_l3.png)
これを積分すれば
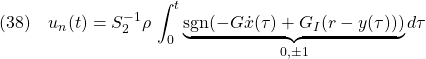
ここで、![]() に注意し、(25)の第1式を用いて
に注意し、(25)の第1式を用いて![]() は
は
![Rendered by QuickLaTeX.com \displaystyle{(39)\quad \begin{array}{l} \underbrace{\dot{x}_1(t)}_{\dot{x}(t)}=\underbrace{(A-BM)}_{\bar{A}_{11}}x_1(t)+\underbrace{BS_2^{-1}}_{\bar{A}_{12}}\underbrace{(S_1x_1(t)+S_2x_2(t))}_{s(t)}\\ =(A-BM)x_1(t)+BS_2^{-1}S_2(Mx_1(t)+x_2(t))\\ =Ax_1(t)+Bx_2(t)\\ =Ax(t)+Bu(t)-\left[\begin{array}{cc} A & B \end{array}\right] \left[\begin{array}{c} x_\infty \\ u_\infty \end{array}\right]\\ =Ax(t)+Bu(t)-\left[\begin{array}{cc} A & B \end{array}\right]S_E^{-1} \left[\begin{array}{c} -w \\ r \end{array}\right]\\ =Ax(t)+Bu(t)-\left[\begin{array}{cc} I & 0 \end{array}\right] \left[\begin{array}{c} -w \\ r \end{array}\right]\\ =Ax(t)+Bu(t)+w \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2ba4e67edf54d3b4672c514eba81c975_l3.png)
となって元の状態方程式となりますが、![]() を無視し、
を無視し、![]() の近似値を使うことも一手段かもしれません。
の近似値を使うことも一手段かもしれません。
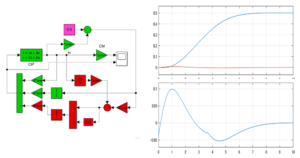
[5] 数値例(1)
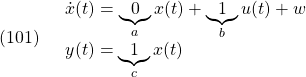
![Rendered by QuickLaTeX.com \displaystyle{(109)\quad \left[\begin{array}{c} -w \\ r \end{array}\right] = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right] }_{S_E} \left[\begin{array}{c} x_\infty \\ u_\infty \end{array}\right] \Rightarrow \left[\begin{array}{c} x_\infty \\ u_\infty \end{array}\right]= \left[\begin{array}{c} r \\ -w \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b6f19bc137b345cd02f056ded5359628_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(111)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{\dot{x}_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right] }_{A_{E3}} \underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-39ef4e33ccbbc6089ea56a80794721bd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(116)\quad s(t)= \underbrace{ \left[\begin{array}{cc} s_1 & s_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{s_2 \left[\begin{array}{cc} m & 1 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} \ (m=s_2^{-1}s_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0f6d44c1de2bf58be8fa0712e50791dd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(117)\quad \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} 1 & 0 \\ s_1 & s_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} 1 & 0 \\ -s_2^{-1}s_1 & s_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ae2c14797a0013427aaf5c62507328fe_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(118)\quad \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{x}'_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} -m & s_2^{-1} \\ -s_1m & m \\ \end{array}\right] }_{T_sA_{E3}T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} + \underbrace{ \left[\begin{array}{cc} 0\\ s_2 \end{array}\right] }_{T_sB_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-09497ea1301736f936b51225906c697c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(123)\quad \begin{array}{l} {\dot u}_\ell(t)= -\underbrace{s_2^{-1}}_{(SB_{E3})^{-1}} \underbrace{(\left[\begin{array}{cc} -s_1m & m \\ \end{array}\right]x'_{E3}(t)-\Phi s(t))}_{(SA_{E3}-\Phi S)x_{E3}(t)}}\\ =-s_2^{-1}(\left[\begin{array}{cc} 0 & ms_2 \\ \end{array}\right]- \left[\begin{array}{cc} \Phi s_1 & \Phi s_2 \\ \end{array}\right])x_{E3}(t)\\ =-s_2^{-1}\left[\begin{array}{cc} -\Phi s_1 & ms_2-\Phi s_2 \\ \end{array}\right]x_{E3}(t)\\ =-\left[\begin{array}{cc} -\Phi m & m-\Phi \\ \end{array}\right] \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right] }_{S_E^{-1}} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)}\\ =-\underbrace{(m-\Phi)}_{f}{\dot x}(t)+\underbrace{m(-\Phi)}_{f_I}(r-y(t))\\ \Rightarrow u_\ell(t)=-fx(t)+f_I\int_0^t (r-y(\tau))d\tau \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6aa7495d1adfe2e01b76d9d8229028e7_l3.png)
![]()
![Rendered by QuickLaTeX.com \displaystyle{(127)\quad \begin{array}{l} {\dot u}_n(t) =-s_2^{-1}\rho\, {\rm sgn}(\underbrace{-\frac{1}{2}\Phi^{-1}}_{p_2} \underbrace{ \left[\begin{array}{cc} s_1 & s_2 \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right] }_{S_E^{-1}} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)})\\ =\rho\, {\rm sgn}(\frac{1}{2}\Phi^{-1} \left[\begin{array}{cc} 1 & m \end{array}\right] \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right])\\ =\rho\, {\rm sgn}(-\underbrace{\frac{1}{2}(-\Phi^{-1})}_{g}{\dot x}(t)+\underbrace{\frac{1}{2}m(-\Phi^{-1})}_{g_I} (r-y(t)))\\ \Rightarrow u_n(t)=\rho\,\int_0^t\underbrace{{\rm sgn}(-g{\dot x}(\tau)+g_I(r-y(\tau)))}_{0,\pm 1}d\tau \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c70ad4d12c7dc10a4700d71c3c2e1719_l3.png)
![]() ,
, ![]() の場合のシミュレーション結果を次に示します。
の場合のシミュレーション結果を次に示します。

[5] 数値例(2)
![Rendered by QuickLaTeX.com \displaystyle{(201)\quad \begin{array}{l} \dot{x}(t)= \underbrace{\left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right]}_{A}x(t) +\underbrace{\left[\begin{array}{cc} 0 \\ 1 \end{array}\right]}_{B}u(t)+ \left[\begin{array}{cc} 0 \\ w \end{array}\right]\\ y(t)=\underbrace{\left[\begin{array}{cc} 1 & 0 \end{array}\right]}_{C}x(t)\\ \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ef113f64e22350dbc52f15182fe1a509_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(209)\quad \left[\begin{array}{c} 0 \\ -w \\ r \end{array}\right] = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{array}\right] }_{S_E} \left[\begin{array}{c} x_{1\infty} \\ x_{2\infty} \\ u_\infty \end{array}\right] \Rightarrow \left[\begin{array}{c} x_{1\infty} \\ x_{2\infty} \\ u_\infty \end{array}\right]= \left[\begin{array}{c} r \\ 0 \\ -w \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-69beeb3b2a284a9be405782120deebbd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(211)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{\dot{x}_{E3}(t)} = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{array}\right] }_{A_{E3}} \underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\right] }_{B_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8e4db6573d9c0866d2409fc3290742b8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(216)\quad \begin{array}{l} s(t)= \underbrace{ \left[\begin{array}{ccc} s_{11} & s_{12} & s_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{s_2 \left[\begin{array}{ccc} m_1 & m_2 & 1 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)}\\ (m_1=s_2^{-1}s_{11},m_2=s_2^{-1}s_{12}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-400eb3876781e6270ec0fdecd65c935f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(217)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} = \underbrace{ \left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ s_{11} & s_{12} & s_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)}\Leftrightarrow\\ \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{ \left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ -s_2^{-1}s_{11} & -s_2^{-1}s_{12} & s_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-967eb06bf641a92d51f2f5dc0823ae03_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(218)\quad \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{x}'_{E3}(t)} = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0\\ -m_1 & -m_2 & s_2^{-1} \\ -s_{12}m_1 & -s_{12}m_2 & m_2 \end{array}\right] }_{T_sA_{E3}T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} + \underbrace{ \left[\begin{array}{cc} 0\\ 0\\ s_2 \end{array}\right] }_{T_sB_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c09c2a528765c494ea49b0e4d526131e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(223)\quad \begin{array}{l} {\dot u}_\ell(t)= -\underbrace{s_2^{-1}}_{(SB_{E3})^{-1}} \underbrace{(\left[\begin{array}{ccc} -s_{12}m_1 & -s_{12}m_2 & m_2 \\ \end{array}\right]x'_{E3}(t)-\Phi s(t))}_{(SA_{E3}-\Phi S)x_{E3}(t)}}\\ =-s_2^{-1}(\left[\begin{array}{ccc} 0 & 0 & m_2s_2 \\ \end{array}\right]- \left[\begin{array}{ccc} \Phi s_{11} & \Phi s_{12} & \Phi s_2 \\ \end{array}\right])x_{E3}(t)\\ =-s_2^{-1}\left[\begin{array}{ccc} -\Phi s_{11} & -\Phi s_{12} & m_2s_2-\Phi s_2 \\ \end{array}\right]x_{E3}(t)\\ =-\left[\begin{array}{ccc} -\Phi m_1 & -\Phi m_2 & m_2-\Phi \\ \end{array}\right] \underbrace{ \left[\begin{array}{ccc} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{array}\right] }_{S_E^{-1}} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)}\\ =-\underbrace{ \left[\begin{array}{cc} -\Phi m_2 & m_2-\Phi \\ \end{array}\right] }_{F}{\dot x}(t)+\underbrace{m_1(-\Phi)}_{F_I}(r-y(t))\\ \Rightarrow u_\ell(t)=-Fx(t)+F_I\int_0^t (r-y(\tau))d\tau \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a5fdce03c67f7578c2ac49db1237f4df_l3.png)
![]()
![Rendered by QuickLaTeX.com \displaystyle{(237)\quad \begin{array}{l} {\dot u}_n(t) =-s_2^{-1}\rho\, {\rm sgn}(\underbrace{-\frac{1}{2}\Phi^{-1}}_{p_2} \underbrace{ \left[\begin{array}{ccc} s_{11} & s_{12} & s_2 \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{ccc} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{array}\right] }_{S_E^{-1}} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)})\\ =s_2^{-1}\rho\, {\rm sgn}(\frac{1}{2}\Phi^{-1} \left[\begin{array}{ccc} s_{12} & s_2 & s_{11} \end{array}\right] \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right])\\ =\rho\, {\rm sgn}(\frac{1}{2}\Phi^{-1} \left[\begin{array}{ccc} m_2 & 1 & m_1 \end{array}\right] \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right])\\ =\rho\, {\rm sgn}(-\underbrace{\frac{1}{2}(-\Phi^{-1}) \left[\begin{array}{cc} m_2 & 1 \end{array}\right] }_{G}{\dot x}(t)+\underbrace{\frac{1}{2}m_1(-\Phi^{-1})}_{G_I} (r-y(t)))\\ \Rightarrow u_n(t)=\rho\,\int_0^t\underbrace{{\rm sgn}(-G{\dot x}(\tau)+G_I(r-y(\tau)))}_{0,\pm 1}d\tau \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fb6f2c2d66db55b55c3690dbc77615f3_l3.png)
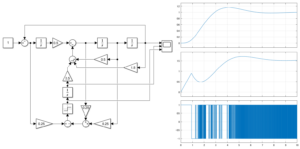
![]() ,
, ![]() の場合のシミュレーション結果を次に示します。
の場合のシミュレーション結果を次に示します。
演習…Flipped Classroom
| MATLAB |
|
| SCILAB |
|