積分動作導入による追従SM制御…Homework
[1] 制御対象
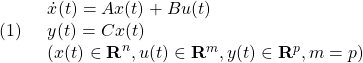
の出力を、コマンド(次式の解)
![]()
に追従させることを考えます(![]() は安定行列)。そのために、積分動作
は安定行列)。そのために、積分動作
![]()
を導入し、次の拡大系を構成します。ここで、(1)はすでに標準形であるとしています。
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \left[\begin{array}{c} \dot x_r(t)\\ \dot x(t) \end{array}\right] = \left[\begin{array}{c|cc} 0 & -C_1 & -C_2\\\hline 0 & A_{11} & A_{12} \\ 0 & A_{21} & A_{22} \end{array}\right] \left[\begin{array}{c} x_r(t)\\ x(t) \end{array}\right] + \left[\begin{array}{c} 0\\\hline 0\\ B_2 \end{array}\right] u(t) + \left[\begin{array}{c} I_m \\\hline 0 \\ 0 \end{array}\right] r(t)\\ (x_r(t)\in{\rm\bf R}^m, x(t)\in{\rm\bf R}^n) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1ab4b378422eddd1bff475a2408082e2_l3.png)
これを、次のように分割し直しても標準形であることには変わりありません。
![Rendered by QuickLaTeX.com \displaystyle{(5a)\quad \begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc|c} 0 & -C_1 & -C_2\\ 0 & A_{11} & A_{12} \\\hline 0 & A_{21} & A_{22} \end{array}\right] }_{A_E} \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0\\ 0\\\hline B_2 \end{array}\right] }_{B_E} u(t) + \left[\begin{array}{c} I_m \\ 0 \\\hline 0 \end{array}\right] r(t)\\ (x_1(t)\in{\rm\bf R}^n, x_2(t)\in{\rm\bf R}^m) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-374491b693fbc08a0a4648abd3e610d2_l3.png)
ただし
![]()
●この積分器による拡大系を安定化できれば、積分器の値![]() は定値となり、被積分項
は定値となり、被積分項![]() の値は零となり、
の値は零となり、![]() は
は![]() へ漸近します。そこで、SM制御によって拡大系を安定化し、追従制御系を構成することを考えます。この制御系は特別な
へ漸近します。そこで、SM制御によって拡大系を安定化し、追従制御系を構成することを考えます。この制御系は特別な![]() の場合を含みますので、まずスイッチング関数として、次式を考えます。
の場合を含みますので、まずスイッチング関数として、次式を考えます。
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} %\underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] %}_{x(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I_m \\ \end{array}\right] }_{S} %\underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] %}_{x(t)} \ (M=S_2^{-1}S_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-01bb686061b94fbab2a0ff90e7d23f64_l3.png)
(5)に対して、座標変換
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} I_n & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right]\\ \Leftrightarrow \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} I_n & 0 \\ -S_2^{-1}S_1 & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-19e5643bcb296d8a517aba35bc4fe14e_l3.png)
を行って、次式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(8a)\quad \begin{array}{l} %\underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] %}_{\dot{x}'(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ S_2\bar{A}_{21} & S_2\bar{A}_{22}S_2^{-1} \\ \end{array}\right] }_{T_sA_ET_s^{-1}} %\underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] %}_{x'(t)} + \underbrace{ \left[\begin{array}{cc} 0\\ S_2B_2 \end{array}\right] }_{T_sB_E} u(t)\\ + \left[\begin{array}{cc} B_r \\ S_1B_r \end{array}\right] r(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a23595fe93cd3fb99284c6e90f61bcf1_l3.png)
ただし
![Rendered by QuickLaTeX.com \displaystyle{(8b)\quad \left\{\begin{array}{l} \bar{A}_{11}= \left[\begin{array}{cc} 0 & -C_1 \\ 0 & A_{11} \end{array}\right] -\left[\begin{array}{c} -C_2\\ A_{12} \end{array}\right]M\\ \bar{A}_{12}= \left[\begin{array}{c} -C_2\\ A_{12} \end{array}\right]S_2^{-1}\\ \bar{A}_{21}=S_2(M\bar{A}_{11} + \left[\begin{array}{cc} 0 & A_{21} \end{array}\right] -A_{22}M)\\ \bar{A}_{22}=S_2(M \left[\begin{array}{c} -C_2\\ A_{12} \end{array}\right] +A_{22})S_2^{-1}\\ B_r=\left[\begin{array}{cc} I_m \\ 0 \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-24d62178408415d07b9cef2c8d0cfab3_l3.png)
ここで、![]() が安定行列となるように行列
が安定行列となるように行列![]() が選ばれているとします。
が選ばれているとします。
●特別な![]() の場合のスライディングモードは
の場合のスライディングモードは![]() で表されますが、一般の
で表されますが、一般の![]() の場合のスライディングモードは
の場合のスライディングモードは
![]()
で表されるとします。ここで、![]() は適当に選択された行列です。
は適当に選択された行列です。
●以上の準備の下で、SM制御則
![]()
を、2次安定性
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \boxed{ \begin{array}{lll} V(\bar{x})= \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t)-S_rr(t) \end{array}\right]^T }_{\bar{x}^T(t)} \underbrace{ \left[\begin{array}{cc} P_1 & 0\\ 0 & P_2 \end{array}\right] }_{P} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t)-S_rr(t) \end{array}\right] }_{\bar{x}(t)}\\ \Rightarrow \dot{V}(\bar{x})\le - \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t)-S_rr(t) \end{array}\right]^T }_{\bar{x}^T(t)} \underbrace{ \left[\begin{array}{cc} Q_1 & 0\\ 0 & I \end{array}\right] }_{Q} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t)-S_rr(t) \end{array}\right] }_{\bar{x}(t)} \end{array}}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-174b6e0b351e183151b07a67d25fe6dc_l3.png)
すなわち
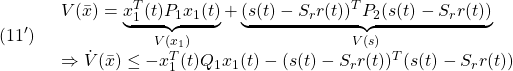
が成り立つように決定します(![]() ,
, ![]() ,
, ![]() )。
)。
[2] 可到達性の検討
ここでは、スライディングモード制御則(10)の具体的な表現を求めます。
●等価制御は、(8)において![]() の場合
の場合
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{cl} (12.1) & s(t)=0\\ \Downarrow &\\ (12.2) & \dot{s}(t)=0\\ \Downarrow &\\ (12.3) & 0=S_2\bar{A}_{21}x_1(t)+S_2\bar{A}_{22}S_2^{-1}s(t)+S_2B_2u(t)\\ \Downarrow &\\ (12.4) & u_{eq}(t)=-\underbrace{(S_2B_2)^{-1}}_{([0\ I]T_sB_E)^{-1}} \underbrace{\left[\begin{array}{cc} S_2\bar{A}_{21} & S_2\bar{A}_{22}S_2^{-1} \\ \end{array}\right]}_{[0\ I]T_sA_ET_s^{-1}} \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]\\ \Downarrow & by\ S=[0\ I]T_s\\ (12.5) & u_{eq}(t)=-(SB_E)^{-1}SA_ET_s^{-1} \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]\\ \Downarrow & by\ (7),(8b)\\ (12.6) & u_{eq}(t)=-(SB_E)^{-1}SA_E \left[\begin{array}{c} x_r(t)\\ x(t) \end{array}\right]} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fc541c88c94f46e054237f8c4eb58974_l3.png)
のように得られます。(10)の第1項![]() は、この等価制御をベースして、(9)を考慮して
は、この等価制御をベースして、(9)を考慮して
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \begin{array}{l} u_\ell(t)=-(S_2B_2)^{-1} (\left[\begin{array}{cc} S_2\bar{A}_{21} & S_2\bar{A}_{22}S_2^{-1} \\ \end{array}\right]\left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]-\Phi s(t))\\ -(S_2B_2)^{-1}(\Phi S_r+S_1B_r)r(t)+(S_2B_2)^{-1}S_r\dot{r}(t)\\ \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-523e59ff1e3266a531c8f91b270e4fc0_l3.png)
すなわち
![Rendered by QuickLaTeX.com \displaystyle{(13')\quad { \boxed{\begin{array}{l} u_\ell(t) =-\underbrace{(SB_E)^{-1}(SA_E-\Phi S)}_{L=L_{eq}+L_\Phi}\left[\begin{array}{c} x_r(t)\\ x(t) \end{array}\right]\\ -\underbrace{(SB_E)^{-1}(\Phi S_r+S_1B_r)}_{L_r} r(t) +\underbrace{(SB_E)^{-1}S_r}_{L_{\dot r}} \dot{r}(t)\\ \end{array}}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2d8158c14705344b0d2033bddb8e59ac_l3.png)
のように構成します(![]() は安定行列)。このとき閉ループ系は次式で与えられます。
は安定行列)。このとき閉ループ系は次式で与えられます。
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \begin{array}{l} \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] = \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ S_2\bar{A}_{21} & S_2\bar{A}_{22}S_2^{-1} \\ \end{array}\right] \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]\\ + \left[\begin{array}{cc} 0\\ S_2B_2 \end{array}\right] (-(S_2B_2)^{-1} (\left[\begin{array}{cc} S_2\bar{A}_{21} & S_2\bar{A}_{22}S_2^{-1} \\ \end{array}\right]\left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]-\Phi s(t))\\ -(S_2B_2)^{-1}(\Phi S_r+S_1B_r)r(t)+(S_2B_2)^{-1}S_r\dot{r}(t)+u_n(t)) + \left[\begin{array}{cc} B_r \\ S_1B_r \end{array}\right] r(t)\\ = \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ S_2\bar{A}_{21} & S_2\bar{A}_{22}S_2^{-1} \\ \end{array}\right] \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]\\ + \left[\begin{array}{cc} 0\\ I_m \end{array}\right] \left[\begin{array}{cc} -S_2\bar{A}_{21} & -S_2\bar{A}_{22}S_2^{-1}+\Phi \\ \end{array}\right] \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]\\ + \left[\begin{array}{cc} 0\\ -(\Phi S_r+S_1B_r)r(t)+S_r\dot{r}(t)+S_2B_2u_n(t) \end{array}\right] + \left[\begin{array}{cc} B_r \\ S_1B_r \end{array}\right] r(t)\\ = \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ 0 & \Phi \\ \end{array}\right] \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]+ \left[\begin{array}{cc} B_rr(t)\\ -\Phi S_rr(t)+S_r\dot{r}(t)+S_2B_2u_n(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7299445c3fbe65641193f7a4c068b664_l3.png)
これを変形して
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{s}(t)-S_r\dot{r}(t) \end{array}\right] = \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ 0 & \Phi \\ \end{array}\right] \left[\begin{array}{c} x_1(t)\\ s(t)-S_rr(t) \end{array}\right]\\ + \left[\begin{array}{cc} B_rr(t)\\ -\Phi S_rr(t)+S_r\dot{r}(t)+S_2B_2u_n(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2cbbaf4d3607cc033e3ec653af8d867e_l3.png)
すなわち、次式が成り立ちます。
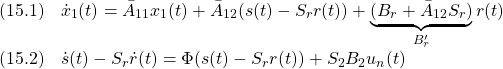
(15.2)に基づいてスライディングモード![]() を達成する
を達成する![]() を明らかにします。
を明らかにします。
![]() は安定行列なので
は安定行列なので
![]()
を満たす![]() を選ぶことができます。これを用いて
を選ぶことができます。これを用いて
![]()
すなわち
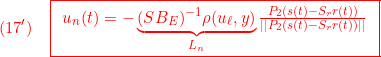
と選びます(![]() )。このとき次式が成り立ち、(11)が示されます。
)。このとき次式が成り立ち、(11)が示されます。
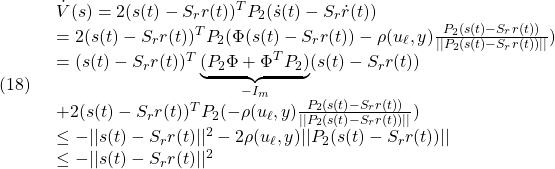
これより(15.2)における2次安定性が成り立つことが分かります。2次安定であれば![]() は0に漸近します。
は0に漸近します。
[3] スライディングモードの検討
次に![]() のもとで、(15.1)から
のもとで、(15.1)から![]() の振舞いについて調べます。
の振舞いについて調べます。
![]() は安定行列なので
は安定行列なので
![]()
を満たす![]() を選ぶことができます。そこで、(15.1)に対するリャプノフ関数
を選ぶことができます。そこで、(15.1)に対するリャプノフ関数![]() の微分について調べます。
の微分について調べます。
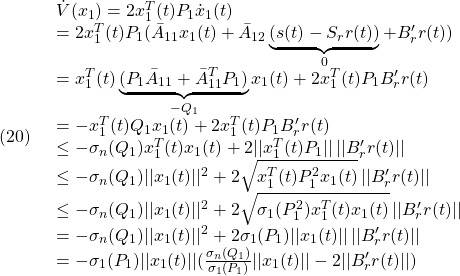
したがって、次式が成り立ち、リャプノフ安定性が示されます。
![]()
これから、ロバスト性での議論と同様に、![]() が発散することはないことが分かります。
が発散することはないことが分かります。
演習C61…Flipped Classroom
| MATLAB |
|
| SCILAB |
|
