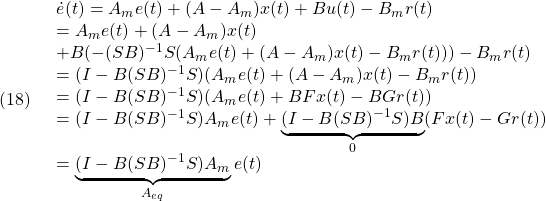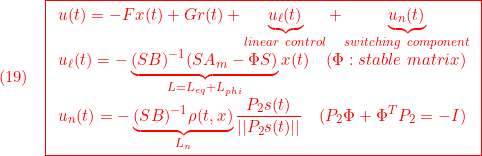モデル規範による追従SM制御…Homework
[1] 次の状態方程式で表される制御対象を考えます。
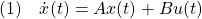
この状態が理想的なモデル
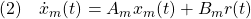
の状態を追従するように、すなわち
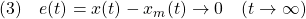
となるように制御則を決定したいとします。
●追従誤差のダイナミックスは
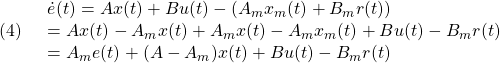
となります。いま条件
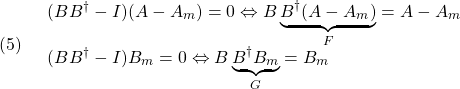
を仮定すると(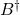 は
は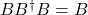 を満たす疑似逆行列)、制御則
を満たす疑似逆行列)、制御則
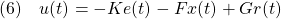
の下では、誤差方程式は次式となります。
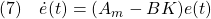
実際、
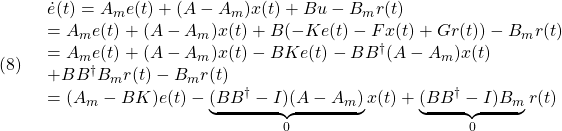
●以上から、制御則(6)の設計の指針として、望ましいモデル(2)を(1)に対する状態フィードバックと入力変換で得るものとします。すなわち
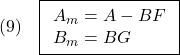
ここで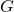 は、
は、 から出力
から出力
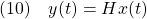
までの定常ゲイン
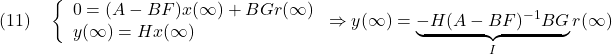
が単位行列となるように、次式で決めます。
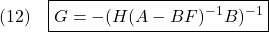
ちなみに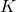 については、(7)が漸近安定であることが前提となり、望ましいモデル(2)より、追従誤差は速いダイナミックスをもつことが必要であることに注意します。
については、(7)が漸近安定であることが前提となり、望ましいモデル(2)より、追従誤差は速いダイナミックスをもつことが必要であることに注意します。
[2] 誤差方程式(4)すなわち
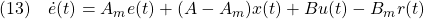
に対して、スライディングモード制御を適用することを考えます。スイッチング関数を
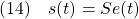
とするとき、スライディングモード時は
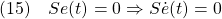
すなわち
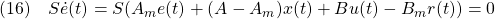
が成り立ち、等価制御は次式となります。
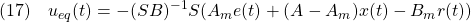
このとき追従誤差のダイナミックスは次式となります。
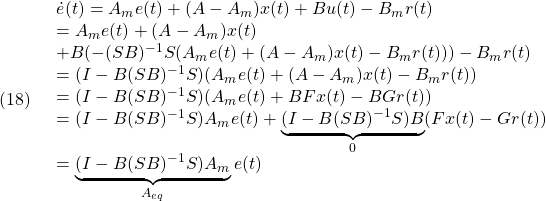
したがって、スライディングモード制御を適用する場合、全体の制御則は、次式で表されます。
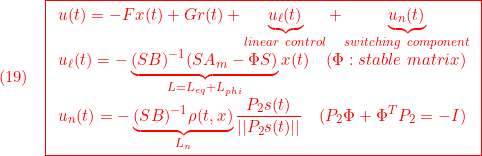
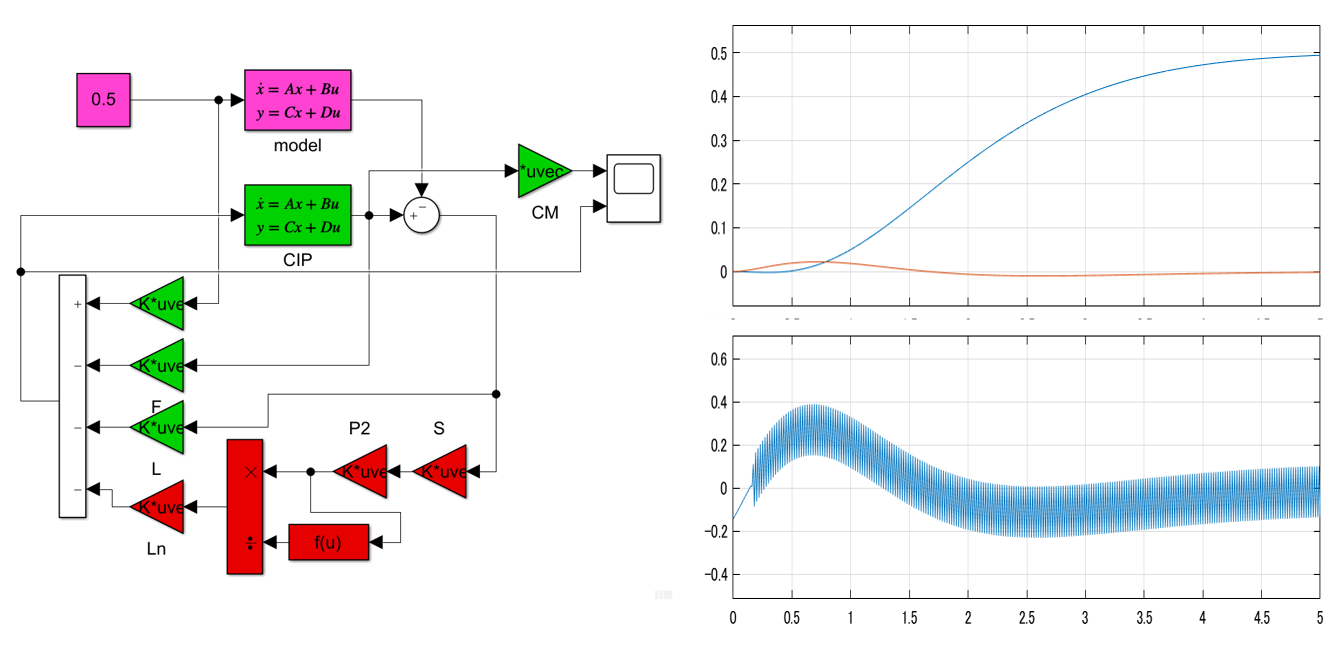
演習C51…Flipped Classroom
| MATLAB |
%cCIP_smcm.m
%-----
clear all, close all
global mc m ell g th0
mc=1; m=0.1; ell=0.2; g=9.8;
ths=0; %input('ths = <0,180> ')/180*pi;
th0=3/180*pi; %input('th(0) = <0,180> ')/180*pi;
%-----
A=[zeros(2,2) eye(2);zeros(2,4)];
A(3,1)=0;
A(3,2)=-3*m*g/(m+4*mc);
A(4,1)=0;
A(4,2)=3*(m+mc)*g/((m+4*mc)*ell);
B=zeros(4,1);
B(3)=4/(m+4*mc);
B(4)=-3/((m+4*mc)*ell);
H=[1 0 0 0];
%-----
lambda=[-0.8*1.5 0.5 -1.5*1.5 1];
nocomp=2;
specpos=rand(4,4);
specent=rand(4,4);
F=vplace2(A,B,lambda,nocomp,specpos,specent)
pl=eig(A-B*F)
%-----
H=[1 0 0 0];
Am=A-B*F;
G=-inv(H*(Am\B));
Bm=B*G;
%-----
Mr=0.5; Mth=3/180*pi;
Tc=1; Tpen=0.25*2*pi*sqrt(2*ell/g);
Q=diag([1/Mr^2,1/Mth^2,Tc^2/Mr^2,Tpen^2/Mth^2]);
S=swflqr(A,B,Q)
%-----
Phi=-0.1;
P2=0.5*inv(-Phi);
Check=P2*Phi+Phi*P2
P2S=P2*S;
Leq=inv(S*B)*S*A;
LPhi=-inv(S*B)*Phi*S;
L=Leq+LPhi;
rho=1;
Ln=inv(S*B)*rho;
%-----
x0=[0;th0*0;0;0];
sim('CIP_smcm_2015a.mdl')
%-----
%eof
|
![]()
![]()
![]()
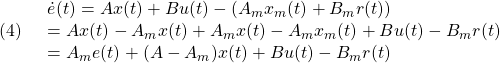
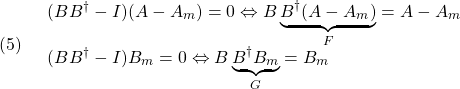
![]() は
は![]() を満たす疑似逆行列)、制御則
を満たす疑似逆行列)、制御則![]()
![]()
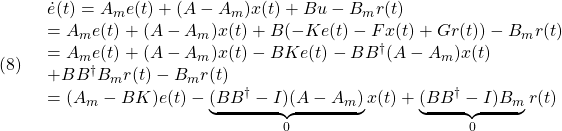
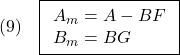
![]() は、
は、![]() から出力
から出力![]()
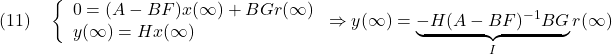
![]()
![]() については、(7)が漸近安定であることが前提となり、望ましいモデル(2)より、追従誤差は速いダイナミックスをもつことが必要であることに注意します。
については、(7)が漸近安定であることが前提となり、望ましいモデル(2)より、追従誤差は速いダイナミックスをもつことが必要であることに注意します。![]()
![]()
![]()
![]()
![]()