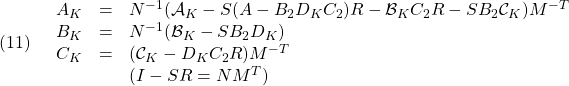| MATLAB |
%b62.m
%-----
clear all, close all
S=1; k=0.1; hs=1; L=10;
a=-k/(2*sqrt(hs)*S); b=1/S; c=1;
wD=L; wI=0.02;
A=[a 0;-c 0]; B1=[0;1]; B2=[b;0];
C1=[0 wI;wD*c*a 0]; D11=[0;0]; D12=[0;wD*c*b];
C2=[c 0;0 1]; D21=[0;0]; D22=[0;0];
%-----
alpha=0.001; r=0.1; th=pi/3;
LMIs=of_synlmi6(A,B1,B2,C1,C2,D11,D12,D21,D22,alpha,r,th);
cobj=zeros(1,decnbr(LMIs));
cobj(1)=1;
[cost,xopt]=mincx(LMIs,cobj);
gopt=dec2mat(LMIs,xopt,1)
R=dec2mat(LMIs,xopt,2);
S=dec2mat(LMIs,xopt,3);
ak=dec2mat(LMIs,xopt,4);
bk=dec2mat(LMIs,xopt,5);
ck=dec2mat(LMIs,xopt,6);
dk=dec2mat(LMIs,xopt,7);
[u,sd,v]=svd(eye(size(A,1))-R*S);
sd=diag(sqrt(1./diag(sd)));
Ni=sd*v'; Mti=u*sd;
AK=Ni*(ak-S*(A-B2*dk*C2)*R-bk*C2*R-S*B2*ck)*Mti;
BK=Ni*(bk-S*B2*dk);
CK=(ck-dk*C2*R)*Mti;
DK=dk;
%-----
pl=eig(A);
ACL=[A+B2*DK*C2 B2*CK;BK*C2 AK];
plCL=eig(ACL)
figure(1)
dregion(-alpha,0,r,th,r*[-2,1,-1,1])
plot(real(pl),imag(pl),'o',real(plCL),imag(plCL),'x')
%-----
ACL=[A+B2*DK*C2 B2*CK;BK*C2 AK];
BCL=[B1+B2*DK*D21;BK*D21];
CCL=[C2(1,:) zeros(1,2)];
AK=[AK BK(:,2);zeros(1,3)];
BK=[BK(:,1) zeros(2,1); -1 1];
CK=[CK DK(:,2)];
DK=[DK(:,1) 0];
%-----
w=logspace(-2,1,100);
H=exp(-L*i*w); ga_H=20*log10(abs(H));
ga_DL=20*log10(abs(H-1));
ga_WT=20*log10(abs(L*i*w));
figure(2)
w=logspace(-3,0,100);
semilogx(w,ga_DL,w,ga_WT),grid, legend('Delta','WT')
%-----
ga_WS=20*log10(abs(wI./(i*w)));
ga_WT=20*log10(abs(wD*(i*w)));
G(:,:)=freqresp(ss(a,b,c,[]),w); G=G.'; ga_G=20*log10(abs(G));
K(:,:)=freqresp(ss(AK,BK(:,1),CK,DK(:,1)),w); K=K.'; ga_K=20*log10(abs(K));
T(:,:)=freqresp(ss(ACL,BCL(:,1),CCL(1,:),[]),w); T=T.'; ga_T=20*log10(abs(T));
ga_S=20*log10(abs(1-T));
figure(3)
subplot(121),semilogx(w,ga_G+ga_K,w,ga_WS,'b',w,-ga_WT,'r'),grid,legend('L=GK','WS','1/WT')
subplot(122),semilogx(w,ga_T,'r',w,-ga_WT,'r',w,ga_S,'b',w,-ga_WS,'b'),grid,legend('T','1/WT','S','1/WS')
%-----
function LMIs=of_synlmi6(A,B1,B2,C1,C2,D11,D12,D21,D22,alpha,r,th)
[n,m]=size(B2); [p,n]=size(C2);
setlmis([]);
gam=lmivar(1,[1 0]);
[R,xxx,Rdec]=lmivar(1,[n 1]);
[S,xxx,Sdec]=lmivar(1,[n 1]);
Ak=lmivar(2,[n n]);
Bk=lmivar(2,[n p]);
Ck=lmivar(2,[m n]);
Dk=lmivar(2,[m p]);
%
lmiRS=newlmi;
lmiterm([lmiRS 1 1 R],A,1,'s'); %#1:R*A'+AR
lmiterm([lmiRS 1 1 Ck],B2,1,'s'); %#1:Ck'*B2'+B2*Ck
lmiterm([lmiRS 2 1 0],A'); %#1:A'
lmiterm([lmiRS 2 1 Ak],1,1); %#1:Ak
lmiterm([lmiRS 2 1 -Dk],C2',B2'); %#1:C2'*Dk'*B2'
lmiterm([lmiRS 2 2 S],1,A,'s'); %#1:A'*S+S*A
lmiterm([lmiRS 2 2 Bk],1,C2,'s'); %#1:C2'*Bk'+Bk*C2
lmiterm([lmiRS 1 3 0],B1); %#1:B1
lmiterm([lmiRS 1 3 Dk],B2,D21); %#1:B2*Dk*D21
lmiterm([lmiRS 2 3 S],1,B1); %#1:S*B1
lmiterm([lmiRS 2 3 Bk],1,D21); %#1:Bk*D21
lmiterm([lmiRS 3 3 gam],-1,1); %#1:-gam
lmiterm([lmiRS 4 1 R],C1,1); %#1:C1*R
lmiterm([lmiRS 4 1 Ck],D12,1); %#1:D12*Ck
lmiterm([lmiRS 4 2 0],C1); %#1:C1
lmiterm([lmiRS 4 2 Dk],D12,C2); %#1:D12*Dk*C2
lmiterm([lmiRS 4 3 0],D11); %#1:D11
lmiterm([lmiRS 4 3 Dk],D12,D21); %#1:D12*Dk*D21
lmiterm([lmiRS 4 4 gam],-1,1); %#1:-gam
%-----
lmiPL1=newlmi;
lmiterm([lmiPL1 1 1 R],A,1,'s'); %#2:R*A'+A*R
lmiterm([lmiPL1 1 1 Ck],B2,1,'s'); %#2:Ck'*B2'+B2*Ck
lmiterm([lmiPL1 2 1 Ak],1,1); %#2:Ak
lmiterm([lmiPL1 1 2 0],A); %#2:A
lmiterm([lmiPL1 1 2 Dk],B2,C2); %#2:B2*Dk*C2
lmiterm([lmiPL1 2 2 S],1,A,'s'); %#2:A'*S+S*A
lmiterm([lmiPL1 2 2 Bk],1,C2,'s'); %#2:C2'*Bk'+Bk*C2
%
lmiterm([lmiPL1 1 1 R],2*alpha,1); %#2:2*alpha*R
lmiterm([lmiPL1 2 1 0],2*alpha); %#2:2*alpha*I
lmiterm([lmiPL1 2 2 S],2*alpha,1); %#2:2*alpha*S
%-----
lmiPL2=newlmi;
lmiterm([lmiPL2 1 1 R],-r,1); %#3:-r*R
lmiterm([lmiPL2 2 1 0],-r); %#3:-r*I
lmiterm([lmiPL2 2 2 S],-r,1); %#3:-r*S
%
lmiterm([lmiPL2 1 3 R],A,1); %#3:A*R
lmiterm([lmiPL2 1 3 Ck],B2,1); %#3:B2*Ck
lmiterm([lmiPL2 2 3 Ak],1,1); %#3:Ak
lmiterm([lmiPL2 1 4 0],A); %#3:A
lmiterm([lmiPL2 1 4 Dk],B2,C2); %#3:B2*Dk*C2
lmiterm([lmiPL2 2 4 S],1,A); %#3:S*A
lmiterm([lmiPL2 2 4 Bk],1,C2); %#3:Bk*C2
%
lmiterm([lmiPL2 3 3 R],-r,1); %#3:-r*R
lmiterm([lmiPL2 4 3 0],-r); %#3:-r*I
lmiterm([lmiPL2 4 4 S],-r,1); %#3:-r*S
%-----
sth=sin(th); cth=cos(th);
lmiPL3=newlmi;
lmiterm([lmiPL3 1 1 R],sth*A,1,'s'); %#4:sth*(R*A'+A*R)
lmiterm([lmiPL3 1 1 Ck],sth*B2,1,'s');%#4:sth*(Ck'*B2'+B2*Ck)
lmiterm([lmiPL3 2 1 Ak],sth,1); %#4:sth*(Ak)
lmiterm([lmiPL3 1 2 0],sth*A); %#4:sth*(A)
lmiterm([lmiPL3 1 2 Dk],sth*B2,C2); %#4:sth*(B2*Dk*C2)
lmiterm([lmiPL3 2 2 S],1,sth*A,'s'); %#4:sth*(A'*S+S*A)
lmiterm([lmiPL3 2 2 Bk],1,sth*C2,'s');%#4:sth*(C2'*Bk'+Bk*C2)
%
lmiterm([lmiPL3 1 3 R],cth*A,1); %#1:cth*(A*R)
lmiterm([lmiPL3 1 3 R],1,-cth*A'); %#1:cth*(-R*A')
lmiterm([lmiPL3 1 3 Ck],cth*B2,1); %#1:cth*(B*Ck)
lmiterm([lmiPL3 1 3 -Ck],-cth*B2',1); %#1:cth*(-Ck'*B')
lmiterm([lmiPL3 2 3 Ak],cth,1); %#4:cth*(Ak)
lmiterm([lmiPL3 1 4 -Ak],-cth,1); %#4:cth*(-Ak')
lmiterm([lmiPL3 1 4 0],A); %#4:cth*(A)
lmiterm([lmiPL3 2 3 0],-A'); %#4:cth*(-A')
lmiterm([lmiPL3 1 4 Dk],cth*B2,C2); %#4:cth*(B2*Dk*C2)
lmiterm([lmiPL3 2 3 -Dk],-cth*C2',B2');%#4:cth*(-C2'*Dk'*B2')
lmiterm([lmiPL3 2 4 S],1,cth*A); %#4:cth*(S*A)
lmiterm([lmiPL3 2 4 S],-cth*A',1); %#4:cth*(-A'*S)
lmiterm([lmiPL3 2 4 Bk],1,cth*C2); %#4:cth*(Bk*C2)
lmiterm([lmiPL3 2 4 -Bk],-cth*C2',1); %#4:cth*(-C2'*Bk')
%
lmiterm([lmiPL3 3 3 R],sth*A,1,'s'); %#4:sth*(R*A'+A*R)
lmiterm([lmiPL3 3 3 Ck],sth*B2,1,'s');%#4:sth*(Ck'*B2'+B2*Ck)
lmiterm([lmiPL3 4 3 Ak],sth,1); %#4:sth*(Ak)
lmiterm([lmiPL3 3 4 0],sth*A); %#4:sth*(A)
lmiterm([lmiPL3 3 4 Dk],sth*B2,C2); %#4:sth*(B2*Dk*C2)
lmiterm([lmiPL3 4 4 S],1,sth*A,'s'); %#4:sth*(A'*S+S*A)
lmiterm([lmiPL3 4 4 Bk],1,sth*C2,'s');%#4:sth*(C2'*Bk'+Bk*C2)
%-----
posX=-newlmi;
lmiterm([posX 1 1 R],1,1); %#5:R
lmiterm([posX 2 1 0],1); %#5:I
lmiterm([posX 2 2 S],1,1); %#5:S
%-----
lmiDk=-newlmi;
lmiterm([lmiDk 1 1 0],1e2); %#6:1e2
lmiterm([lmiDk 2 2 0],1e2); %#6:1e2
lmiterm([lmiDk 2 1 Dk],1,1); %#6:Dk
%-----
lmig=newlmi;
lmiterm([lmig,1,1,gam],1,1); %#7:gam
lmiterm([lmig,1,1,0],-1e3); %#7:1e3
LMIs=getlmis;
end
%-----
%eof
|
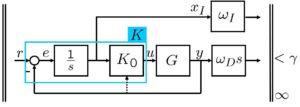
![]() 制御系を設計する際の2ポートシステムの構成法について述べます。
制御系を設計する際の2ポートシステムの構成法について述べます。
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \boxed{P: \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x} \\ \dot{x}_I \end{array}\right]= \underbrace{ \left[\begin{array}{cc} A& 0 \\ -C & 0 \end{array}\right] }_{A} \left[\begin{array}{c} x \\ x_I \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B_1} r + \underbrace{\left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_2} u\\ \underbrace{ \left[\begin{array}{c} y_{11} \\ y_{12} \end{array}\right] }_{y_1} = \underbrace{ \left[\begin{array}{cc} 0 &\omega_I\\ \omega_DCA & 0 \end{array}\right] }_{C_1} \left[\begin{array}{c} x \\ x_I \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \end{array}\right] }_{D_{11}} r + \underbrace{ \left[\begin{array}{c} 0 \\ \omega_DCB \end{array}\right] }_{D_{12}} u\\ \underbrace{ \left[\begin{array}{c} y \\ x_I \end{array}\right] }_{y_2} = \underbrace{ \left[\begin{array}{cc} C & 0\\ 0 & 1 \end{array}\right] }_{C_2} \left[\begin{array}{c} x \\ x_I \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \end{array}\right] }_{D_{21}} r \end{array}\right.} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ff652eebac0dfbfce980306520dacf5b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad K_0: \left\{\begin{array}{l} \dot{x}_K=A_Kx_K+ \underbrace{ \left[\begin{array}{cc} B_{K1} & B_{K2} \end{array}\right] }_{B_K} \left[\begin{array}{c} y \\ x_I \end{array}\right] \\ u=C_Kx_K + \underbrace{ \left[\begin{array}{cc} D_{K1} & D_{K2} \end{array}\right] }_{D_K} \left[\begin{array}{c} y \\ x_I \end{array}\right] \end{array}\right.}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7dd72681c4a7787121d7e37cfd799a36_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad P_{CL}: \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x} \\ \dot{x}_K \end{array}\right] = \underbrace{ \left[\begin{array}{ccc} A+B_2D_KC_2 & B_2C_K \\ B_KC_2 & A_K \end{array}\right] }_{A_{CL}} \left[\begin{array}{c} x \\ x_K \end{array}\right] + \underbrace{ \left[\begin{array}{ccc} B_1+B_2D_KD_{21} \\ B_KD_{21} \end{array}\right] }_{B_{CL}} r\\ \underbrace{ \left[\begin{array}{c} y_{11} \\ y_{12} \end{array}\right] }_{y_1} = \underbrace{ \left[\begin{array}{ccc} C_1+D_{12}D_KC_2 & D_{12}C_K \end{array}\right] }_{C_{CL}} \left[\begin{array}{c} x \\ x_K \end{array}\right] + \underbrace{ (D_{11}+D_{12}D_KD_{21}) }_{D_{CL}} r \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-741714e54da8d9e0f2096a7a04b58fe2_l3.png)
![]() ノルムが
ノルムが![]() より小、すなわち
より小、すなわち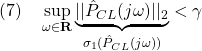
![]()
![]() を求める問題を考えます。
を求める問題を考えます。![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \begin{array}{l} \left[\begin{array}{cc} AR+B_2{\cal C}_K & A+B_2D_KC_2\\ {\cal A}_K & SA+{\cal B}_KC_2 \end{array}\right] +(*)^T %\nonumber\\&& +\alpha \left[\begin{array}{cc} R & I \\ I & S \end{array}\right]<0}\\ \left[\begin{array}{cc} -r \left[\begin{array}{cc} R & I \\ I & S \end{array}\right] & \left[\begin{array}{cc} AR+B_2{\cal C}_K & A+B_2D_KC_2\\ {\cal A}_K & SA+{\cal B}_KC_2 \end{array}\right] \\ (*)^T & -r \left[\begin{array}{cc} R & I \\ I & S \end{array}\right] \end{array}\right] <0\\ \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right]\otimes \left[\begin{array}{cc} AR+B_2{\cal C}_K & A+B_2D_KC_2\\ {\cal A}_K & SA+{\cal B}_KC_2 \end{array}\right]+ (*)^T <0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4b17321a2dbe748dbe61f89fa2ec2fe7_l3.png)
![]() に積分器
に積分器![]()
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \boxed{K: \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_K \\ \dot{x}_I \end{array}\right]= \left[\begin{array}{cc} A_K & B_{K2} \\ 0 & 0 \end{array}\right] \left[\begin{array}{c} x_K \\ x_I \end{array}\right] + \left[\begin{array}{cc} B_{K1} & 0\\ -1& 1 \end{array}\right] \left[\begin{array}{c} y \\ r \end{array}\right] \\ u= \left[\begin{array}{cc} C_K & D_{K2} \end{array}\right] \left[\begin{array}{c} x_K \\ x_I \end{array}\right] + \left[\begin{array}{cc} D_{K1} & 0 \end{array}\right] \left[\begin{array}{c} y \\ r \end{array}\right] \end{array}\right.} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5af64f9178784ac387be596d890834e7_l3.png)
![]()
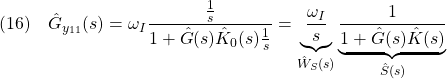
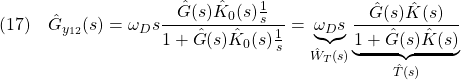
![]()
![]()
![]()
![]() 水タンクにおいて、バルブに無駄時間がある場合の次の状態方程式を考えます。
水タンクにおいて、バルブに無駄時間がある場合の次の状態方程式を考えます。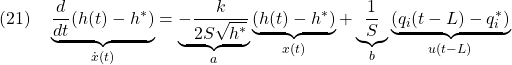
![]() 制御系を設計する次のプログラムを実行して得られる3枚の図の意味について説明せよ。
制御系を設計する次のプログラムを実行して得られる3枚の図の意味について説明せよ。![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \left[\begin{array}{ccc} \left[\begin{array}{cc} AR+B_2{\cal C}_K & A+B_2D_KC_2\\ {\cal A}_K & SA+{\cal B}_KC_2 \end{array}\right]+(*)^T & \left[\begin{array}{c} B_1+B_2D_KD_{21} \\ SB_1+{\cal B}_KD_{21} \end{array}\right] & (*)^T \\ (*)^T & -\gamma^2 I & (*)^T \\ \left[\begin{array}{cc} C_1R+D_{12}{\cal C}_K & C_1+D_{12}D_KC_2 \end{array}\right] & D_{11} & -I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-70227b027ea2dc86414260352f2ab59c_l3.png)