性能解析LMI（Ｈ２ノルム）

性能解析LMI（Ｈ２ノルム）…Homework

[1]　直達項をもたない $n$ 次系の $H_2$ ノルムが $\gamma$ より小である条件は ${\rm\bf LMI}$ を用いて、次のように表されます。

図1　直達項をもたないｎ次系

$\displaystyle{ \begin{array}{l} \displaystyle{{\rm tr} (CW_cC^T)<\gamma^2}\\\\ \displaystyle{\Leftrightarrow \exists X_c>0,\ Q_c>0:\\ (1a)\quad\left[\begin{array}{cc} A^TX_c+X_cA & X_cB \\ B^TX_c & -I \end{array}\right]<0,\ \left[\begin{array}{cc} X_c & C^T \\ C & Q_c \end{array}\right]>0,\ {\rm tr}(Q_c)<\gamma^2}\\\\ \displaystyle{\Leftrightarrow \exists Y_c>0,\ Q_c>0:\\ (1b)\quad \left[\begin{array}{cc} Y_cA^T+AY_c & Y_cB \\ B^TY_c & -I \end{array}\right]<0,\ \left[\begin{array}{cc} Y_c & Y_cC^T \\ CY_c & Q_c \end{array}\right]>0,\ {\rm tr}(Q_c)<\gamma^2} \end{array}}$

$\displaystyle{ \begin{array}{l} \displaystyle{{\rm tr} (B^TW_oB)<\gamma^2}\\\\ \displaystyle{\Leftrightarrow \exists X_o>0,\ Q_o>0:\\ (2a)\quad\left[\begin{array}{cc} AX_o+X_oA^T & X_oC^T \\ CX_o & -I \end{array}\right]<0,\ \left[\begin{array}{cc} X_o & B \\ B^T & Q_o \end{array}\right]>0,\ {\rm tr}(Q_o)<\gamma^2}\\\\ \displaystyle{\Leftrightarrow \exists Y_o>0,\ Q_o>0:\\ (2b)\quad\left[\begin{array}{cc} Y_oA+A^TY_o & Y_oC^T \\ CY_o & -I \end{array}\right]<0,\ \left[\begin{array}{cc} Y_o & Y_oB \\ B^TY_o & Q_o \end{array}\right]>0,\ {\rm tr}(Q_o)<\gamma^2} \end{array}}$

ここで、 $W_c$ と $W_o$ はそれぞれ

$(3)\quad \begin{array}{l} \displaystyle{W_c=\int_0^\infty \exp(At)BB^T\exp(A^Tt)dt}\\ \displaystyle{W_o=\int_0^\infty \exp(A^Tt)C^TC\exp(At)dt} \end{array} }$

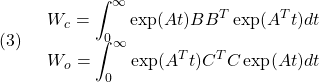
で与えられ、次式が成り立つことに注意します。

$(4)\quad \begin{array}{l} {\rm tr} (CW_cC^T)={\rm tr} (B^TW_oB) \end{array} }$

さて、 $W_c$ と $W_o$ はそれぞれリャプノフ方程式

$\displaystyle{(5)\quad \begin{array}{l} W_cA^T+AW_c+BB^T=0\\ W_oA+A^TW_o+C^TC=0 \end{array} }$

の解であることから

$\displaystyle{(6)\quad \begin{array}{l} V_cA^T+AV_c+BB^T<0\\ V_oA+A^TV_o+C^TC<0 \end{array} }$

を満たす $V_c$ と $V_o$ に対して、 $X_c=V_c^{-1}$ 、 $X_o=V_o^{-1}$ とおくと

$\displaystyle{(7)\quad \begin{array}{l} A^TX_c+X_cA+X_cBB^TX_c<0 \Leftrightarrow\ \left[\begin{array}{cc} A^TX_c+X_cA & X_cB \\ B^TX_c & -I \end{array}\right]<0 \\ AX_o+X_oA^T+X_oC^TCX_o<0 \Leftrightarrow\ \left[\begin{array}{cc} AX_o+X_oA^T & X_oC^T \\ CX_o & -I \end{array}\right]<0 \end{array} }$

が成り立ちます。一方、(6)と(5)から

$\displaystyle{(8)\quad \begin{array}{l} V_cA^T+AV_c+BB^T=(V_c-W_c)A^T+A(V_c-W_c)<0\\ V_oA+A^TV_o+C^T=(V_o-W_o)A+A^T(V_o-W_o)<0 \end{array} }$

となって、次を得ます。

$\displaystyle{(9)\quad \begin{array}{l} V_c-W_c=X_c^{-1}-W_c>0\\ V_o-W_o=X_o^{-1}-W_o>0 \end{array} }$

以上の準備の下で、次を示します。

$\displaystyle{(10)\quad \begin{array}{l} {\rm tr} (CW_cC^T)<\gamma^2 \Leftrightarrow\ \left[\begin{array}{cc} X_c & C^T \\ C & Q_c \end{array}\right]>0,\ {\rm tr} (Q_c)<\gamma^2\\ {\rm tr} (B^TW_oB)<\gamma^2 \Leftrightarrow\ \left[\begin{array}{cc} X_o & B \\ B^T & Q_o \end{array}\right]>0,\ {\rm tr} (Q_o)<\gamma^2 \end{array} }$

まず必要性については、(9)から、十分小さな $\epsilon>0$ を選んで

$\displaystyle{(11)\quad \begin{array}{l} CX_c^{-1}C^T-(CW_cC^T+\epsilon I)>0 \Leftrightarrow\ \left[\begin{array}{cc} X_c & C^T \\ C & CW_cC^T+\epsilon I \end{array}\right]>0\\ B^TX_o^{-1}B-(B^TW_oB+\epsilon I)>0 \Leftrightarrow\ \left[\begin{array}{cc} X_o & B \\ B^T & B^TW_oB+\epsilon I \end{array}\right]>0 \end{array} }$

および

$(12)\quad \begin{array}{l} {\rm tr} (CW_cC^T+\epsilon I)<\gamma^2\\ {\rm tr} (B^TW_oB+\epsilon I)<\gamma^2 \end{array} }$

を満足させることができます。ここで、 $Q_c=CW_cC^T+\epsilon I$ 、 $Q_o=B^TW_oB+\epsilon I$ とおきます。次に十分性については、 $Q_c=CW_cC^T$ 、 $Q_o=B^TW_oB$ の場合を考えれば自明です。

●以上では、次のシュール補元に関する公式を多用しました。

$\displaystyle{\boxed{ \begin{array}{lll} && \left[\begin{array}{cc} P & M \\ M^T & Q \end{array}\right]<0\\ &\Leftrightarrow& P-MQ^{-1}M^T<0,\ Q<0\\ &\Leftrightarrow& P<0,\ Q-M^TP^{-1}M<0 \end{array} }}$

$\displaystyle{\boxed{ \begin{array}{lll} && \left[\begin{array}{cc} P & M \\ M^T & Q \end{array}\right]>0\\ &\Leftrightarrow& MQ^{-1}M^T-P>0,\ Q>0\\ &\Leftrightarrow& P>0,\ M^TP^{-1}M-Q>0 \end{array} }}$

演習B23…Flipped Classroom

$1^\circ$ １次遅れ系に対して、適当な $\gamma$ を設定し、 $H_2$ ノルムとの大小関係をチェックするプログラムを作成せよ。

MATLAB

%ana_lmi6.m
%------
 clear all, close all
 T=1; K=1;
 A=-1/T; B=K/T; 
 C=1; D=0; 
 n=1; m=1; p=1; 
 CT=1;
 gam=1 %input('gamma =  '); 
%------
 setlmis([]);
 X=lmivar(1,[n 1]);
 Q=lmivar(1,[n 1]);
%------
 lmi1=newlmi;   
 lmiterm([lmi1 1 1 X],1,A,'s'); %#1:X*A+A'*X 
 lmiterm([lmi1 1 2 X],1,B);     %#1:X*B 
 lmiterm([lmi1 2 2 0],-1);      %#1:-I
%------
 lmi2=newlmi;  
 lmiterm([-lmi2 1 1 X],1,1);    %#2:X 
 lmiterm([-lmi2 1 2 0],C');     %#2:C' 
 lmiterm([-lmi2 2 2 Q],1,1);    %#2:Q
%------ 
 lmi3=newlmi;   
 lmiterm([-lmi3 1 1 X],1,1);    %#3:X>0
%------ 
 lmi4=newlmi;   
 lmiterm([-lmi4 1 1 Q],1,1);    %#4:Q>0 
%------ 
 lmi5=newlmi;   
 lmiterm([lmi5 1 1 Q],CT,1);    %#5:tr(Q)=CT*Q
 lmiterm([lmi5 1 1 0],-gam^2);  %#5:-gam^2
%------ 
 LMIs=getlmis; 
 [tmin,xfeas]=feasp(LMIs);
 X=dec2mat(LMIs,xfeas,X) 
 Q=dec2mat(LMIs,xfeas,Q) 
%------
%eof

制御系CAD

制御を意識したモノつくりを目指して

性能解析LMI（Ｈ２ノルム）